Deck 14: Review
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/228
Play
Full screen (f)
Deck 14: Review
1
Find the distance d( .
-
A) 4
B)
C)
D) 106
-
A) 4
B)
C)
D) 106
2
Plot the point.
-
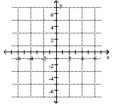
A)
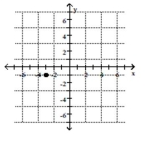
B)
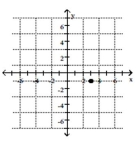
C)
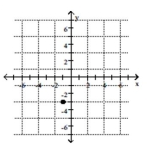
D)
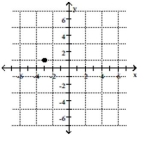
-

A)

B)

C)

D)


3
Plot the point.
-
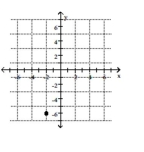
A)
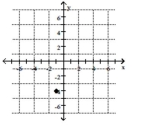
B)
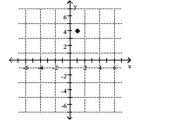
C)
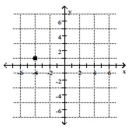
D)
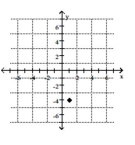
-

A)

B)

C)

D)


4
Find the distance d( .
-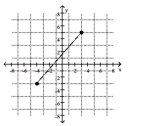
A)
B) 56
C) 1
D)
-

A)
B) 56
C) 1
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
5
Tell in which quadrant or on what coordinate axis the point lies.
(-16, 14)
A) Quadrant III
B) Quadrant II
C) Quadrant I
D) Quadrant IV
(-16, 14)
A) Quadrant III
B) Quadrant II
C) Quadrant I
D) Quadrant IV

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
6
Find the distance d( .
-
A) 6
B)
C) 5
D) 4
-
A) 6
B)
C) 5
D) 4

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
7
Tell in which quadrant or on what coordinate axis the point lies.
(-10, -6)
A) Quadrant IV
B) Quadrant II
C) Quadrant III
D) Quadrant I
(-10, -6)
A) Quadrant IV
B) Quadrant II
C) Quadrant III
D) Quadrant I

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
8
Find the distance d( .
-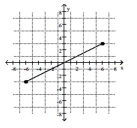
A) 108
B)
C)
D) 6
-

A) 108
B)
C)
D) 6

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
9
Plot the point.
-
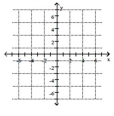
A)
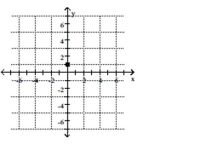
B)
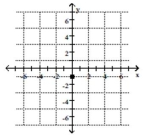
C)
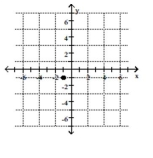
D)
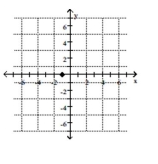
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
10
Plot the point.
-
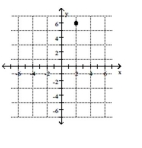
A)
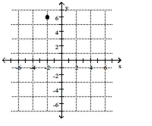
B)
C)
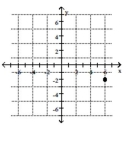
D)

-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
11
Tell in which quadrant or on what coordinate axis the point lies.
(-7, 0)
A) x-axis
B) Quadrant II
C) Quadrant I
D) y-axis
(-7, 0)
A) x-axis
B) Quadrant II
C) Quadrant I
D) y-axis

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
12
Plot the point.
-
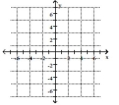
A)
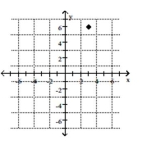
B)
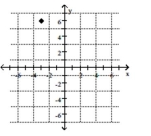
C)
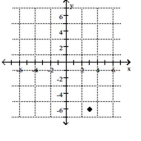
D)
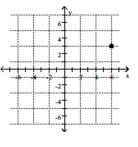
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
13
Find the distance d( .
-
A)
B) 25
C) 5
D) 8
-
A)
B) 25
C) 5
D) 8

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
14
Tell in which quadrant or on what coordinate axis the point lies.
(0, -6)
A) x-axis
B) y-axis
C) Quadrant I
D) Quadrant II
(0, -6)
A) x-axis
B) y-axis
C) Quadrant I
D) Quadrant II

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
15
Find the distance d( .
-
A) 100
B) 20
C) 11
D) 10
-
A) 100
B) 20
C) 11
D) 10

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
16
Tell in which quadrant or on what coordinate axis the point lies.
(12, -13)
A) Quadrant II
B) Quadrant I
C) Quadrant III
D) Quadrant IV
(12, -13)
A) Quadrant II
B) Quadrant I
C) Quadrant III
D) Quadrant IV

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
17
Plot the point.
-
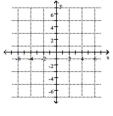
A)
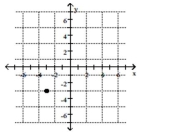
B)
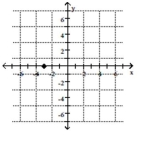
C)
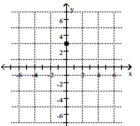
D)
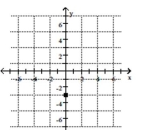
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
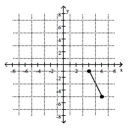
18
Find the distance d( .
-
A) 6
B)
C)
D) 12
-

A) 6
B)
C)
D) 12

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
19
Tell in which quadrant or on what coordinate axis the point lies.
(6, 17)
A) Quadrant II
B) Quadrant I
C) Quadrant III
D) Quadrant IV
(6, 17)
A) Quadrant II
B) Quadrant I
C) Quadrant III
D) Quadrant IV

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
20
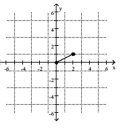
Find the distance d( .
-
A) 0
B) 2
C) 1
D)
-

A) 0
B) 2
C) 1
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
21
Decide whether or not the points are the vertices of a right triangle.
(1, -3), (7, -1), (13, -8)
A) Yes
B) No
(1, -3), (7, -1), (13, -8)
A) Yes
B) No

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
22
Find the midpoint of the line segment joining the points
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
23
Find the distance d( .
- Round to three decimal places, if necessary.
A)
B)
C)
D)
- Round to three decimal places, if necessary.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the problem.
-Find all values of k so that the given points are units apart. (-5, 5), (k, 0)
A) 7
B) 3, 7
C) -3, -7
D) -7
-Find all values of k so that the given points are units apart. (-5, 5), (k, 0)
A) 7
B) 3, 7
C) -3, -7
D) -7

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
25
Find the midpoint of the line segment joining the points
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
26
Find the distance d( .
-
A) 48
B)
C) 4
D)
-
A) 48
B)
C) 4
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
27
Find the midpoint of the line segment joining the points
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
28
Find the midpoint of the line segment joining the points
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
29
Find the midpoint of the line segment joining the points
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the problem.
Find all the points having an x-coordinate of 9 whose distance from the point (3, -2) is 10.
A) (9, -12), (9, 8)
B) (9, 13), (9, -7)
C) (9, 2), (9, -4)
D) (9, 6), (9, -10)
Find all the points having an x-coordinate of 9 whose distance from the point (3, -2) is 10.
A) (9, -12), (9, 8)
B) (9, 13), (9, -7)
C) (9, 2), (9, -4)
D) (9, 6), (9, -10)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.
-Find the area of the right triangle ABC with A = (-2, 7), B = (7, -1), C = (3, 9).
A) square units
B) 29 square units
C) 58 square units
D) square units
-Find the area of the right triangle ABC with A = (-2, 7), B = (7, -1), C = (3, 9).
A) square units
B) 29 square units
C) 58 square units
D) square units

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
32
Find the midpoint of the line segment joining the points
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
33
Find the distance d( .
-
A) 4
B) 32
C)
D)
-
A) 4
B) 32
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
34
Decide whether or not the points are the vertices of a right triangle.
(-1, 7), (6, 7), (6, 9)
A) Yes
B) No
(-1, 7), (6, 7), (6, 9)
A) Yes
B) No

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the problem.
-Find the length of each side of the triangle determined by the three points . State whether the triangle is an isosceles triangle, a right triangle, neither of these, or both.
A) neither
B) right triangle
C) both
D) isosceles triangle
-Find the length of each side of the triangle determined by the three points . State whether the triangle is an isosceles triangle, a right triangle, neither of these, or both.
A) neither
B) right triangle
C) both
D) isosceles triangle

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
36
Find the distance d( .
-
A) 5
B)
C) 24
D)
-
A) 5
B)
C) 24
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
37
Decide whether or not the points are the vertices of a right triangle.
(6, 12), (8, 16), (10, 15)
A) No
B) Yes
(6, 12), (8, 16), (10, 15)
A) No
B) Yes

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the problem.
A middle school's baseball playing field is a square, 55 feet on a side. How far is it directly from home plate to second base (the diagonal of the square)? If necessary, round to the nearest foot.
A) 85 feet
B) 79 feet
C) 78 feet
D) 77 feet
A middle school's baseball playing field is a square, 55 feet on a side. How far is it directly from home plate to second base (the diagonal of the square)? If necessary, round to the nearest foot.
A) 85 feet
B) 79 feet
C) 78 feet
D) 77 feet

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
39
Decide whether or not the points are the vertices of a right triangle.
(8, -7), (14, -5), (13, -10)
A) Yes
B) No
(8, -7), (14, -5), (13, -10)
A) Yes
B) No

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the problem.
-A motorcycle and a car leave an intersection at the same time. The motorcycle heads north at an average speed of 20 miles per hour, while the car heads east at an average speed of 48 miles per hour. Find an expression for
Their distance apart in miles at the end of t hours.
A) miles
B) miles
C) miles
D) miles
-A motorcycle and a car leave an intersection at the same time. The motorcycle heads north at an average speed of 20 miles per hour, while the car heads east at an average speed of 48 miles per hour. Find an expression for
Their distance apart in miles at the end of t hours.
A) miles
B) miles
C) miles
D) miles

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
If (7, -6) is the endpoint of a line segment, and (2, -5) is its midpoint, find the other endpoint.
A) (-3, -4)
B) (9, -16)
C) (-3, -7)
D) (17, -8)
If (7, -6) is the endpoint of a line segment, and (2, -5) is its midpoint, find the other endpoint.
A) (-3, -4)
B) (9, -16)
C) (-3, -7)
D) (17, -8)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
42
Determine whether the given point is on the graph of the equation.
-Equation:
Point:
A) Yes
B) No
-Equation:
Point:
A) Yes
B) No

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem.
If (-7, -3) is the endpoint of a line segment, and (-3, -5) is its midpoint, find the other endpoint.
A) (-11, 5)
B) (-15, 1)
C) (1, -7)
D) (1, -1)
If (-7, -3) is the endpoint of a line segment, and (-3, -5) is its midpoint, find the other endpoint.
A) (-11, 5)
B) (-15, 1)
C) (1, -7)
D) (1, -1)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
44
List the intercepts of the graph.
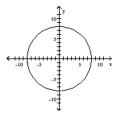
A) (-8, 0), (0, 8)
B) (-8, 0), (0, -8), (0, 0), (0, 8), (8, 0)
C) (0, 8), (8, 0)
D) (-8, 0), (0, -8), (0, 8), (8, 0)

A) (-8, 0), (0, 8)
B) (-8, 0), (0, -8), (0, 0), (0, 8), (8, 0)
C) (0, 8), (8, 0)
D) (-8, 0), (0, -8), (0, 8), (8, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
45
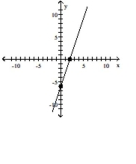
Graph the equation by plotting points.
-
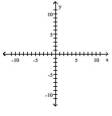
A)
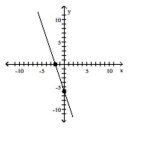
B)
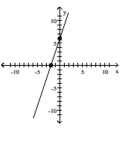
C)
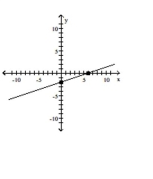
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the problem.
If (1, -4) is the endpoint of a line segment, and (3, 1) is its midpoint, find the other endpoint.
A) (11, 0)
B) (5, 6)
C) (5, -9)
D) (-3, -14)
If (1, -4) is the endpoint of a line segment, and (3, 1) is its midpoint, find the other endpoint.
A) (11, 0)
B) (5, 6)
C) (5, -9)
D) (-3, -14)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
47
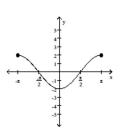
List the intercepts of the graph.
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
48
List the intercepts of the graph.
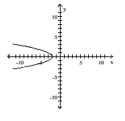
A) (0, 2)
B) (0, -2)
C) (-2, 0)
D) (2, 0)

A) (0, 2)
B) (0, -2)
C) (-2, 0)
D) (2, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the problem.
If (5, 3) is the endpoint of a line segment, and (1, 1) is its midpoint, find the other endpoint.
A) (13, 7)
B) (-3, 5)
C) (1, -5)
D) (-3, -1)
If (5, 3) is the endpoint of a line segment, and (1, 1) is its midpoint, find the other endpoint.
A) (13, 7)
B) (-3, 5)
C) (1, -5)
D) (-3, -1)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.
-If is a point on the graph of , what is ?
A)
B)
C)
D) 4
-If is a point on the graph of , what is ?
A)
B)
C)
D) 4

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
51
Determine whether the given point is on the graph of the equation.
-Equation: y Point: (1, 0)
A) Yes
B) No
-Equation: y Point: (1, 0)
A) Yes
B) No

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
52
Graph the equation by plotting points.
-
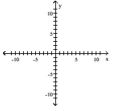
A)
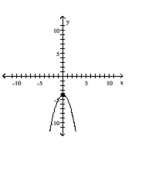
B)
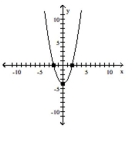
C)
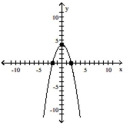
D)
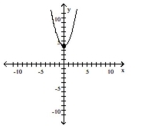
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem.
If (a, 3) is a point on the graph of y = 2x - 5, what is a?
A) -1
B) -4
C) 4
D) 1
If (a, 3) is a point on the graph of y = 2x - 5, what is a?
A) -1
B) -4
C) 4
D) 1

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
54
List the intercepts of the graph.
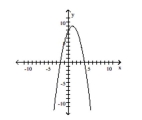
A) (0, -2), (8, 0), (0, 4)
B) (0, -2), (0, 8), (4, 0)
C) (-2, 0), (0, 8), (4, 0)
D) (-2, 0), (0, 8), (0, 4)

A) (0, -2), (8, 0), (0, 4)
B) (0, -2), (0, 8), (4, 0)
C) (-2, 0), (0, 8), (4, 0)
D) (-2, 0), (0, 8), (0, 4)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
55
Graph the equation by plotting points.
-
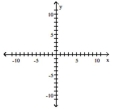
A)
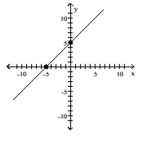
B)
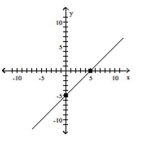
C)
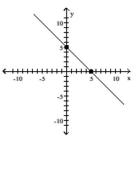
D)
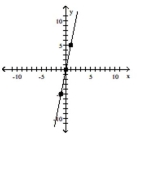
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
56
List the intercepts of the graph.
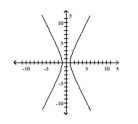
A) (0, -1), (0, 1)
B) (0, -1), (1, 0)
C) (-1, 0), (0, 1)
D) (-1, 0), (1, 0)

A) (0, -1), (0, 1)
B) (0, -1), (1, 0)
C) (-1, 0), (0, 1)
D) (-1, 0), (1, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
57
Graph the equation by plotting points.
-
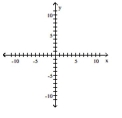
A)
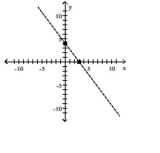
B)
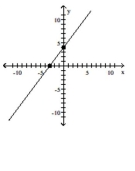
C)
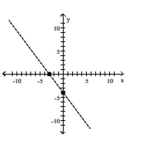
D)
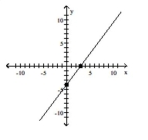
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the problem.
-The medians of a triangle intersect at a point. The distance from the vertex to the point is exactly two-thirds of the distance from the vertex to the midpoint of the opposite side. Find the exact distance of that point from the
Vertex A(3, 4) of a triangle, given that the other two vertices are at (0, 0) and (8, 0).
A)
B)
C)
D) 2
-The medians of a triangle intersect at a point. The distance from the vertex to the point is exactly two-thirds of the distance from the vertex to the midpoint of the opposite side. Find the exact distance of that point from the
Vertex A(3, 4) of a triangle, given that the other two vertices are at (0, 0) and (8, 0).
A)
B)
C)
D) 2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
59
List the intercepts of the graph.
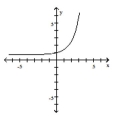
A) (0, 1)
B) (1, 0)
C) (0, 0)
D) (1, 1)

A) (0, 1)
B) (1, 0)
C) (0, 0)
D) (1, 1)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
60
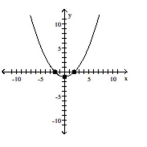
Graph the equation by plotting points.
-
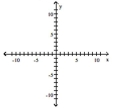
A)

B)
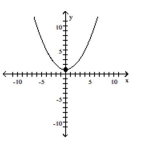
C)
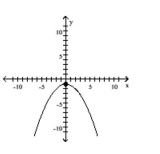
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
61
List the intercepts of the graph.Tell whether the graph is symmetric with respect to the x-axis, y-axis, origin, or none of
these.
-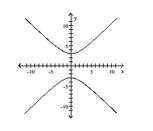
A) intercepts: and
symmetric with respect to -axis
B) intercepts: and
symmetric with respect to origin
C) intercepts: and
symmetric with respect to -axis, -axis, and origin
D) intercepts: and
symmetric with respect to -axis, -axis, and origin
these.
-

A) intercepts: and
symmetric with respect to -axis
B) intercepts: and
symmetric with respect to origin
C) intercepts: and
symmetric with respect to -axis, -axis, and origin
D) intercepts: and
symmetric with respect to -axis, -axis, and origin

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
62
Plot the point A. Plot the point B that has the given symmetry with point A.
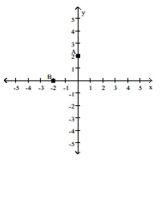
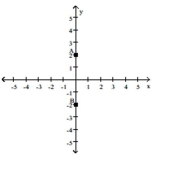
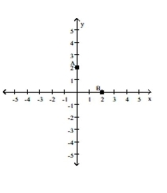
-A = (0, 2); B is symmetric to A with respect to the origin
A)
B)
C)
D)
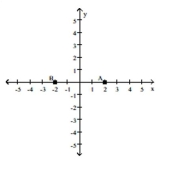
-A = (0, 2); B is symmetric to A with respect to the origin

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
63
List the intercepts for the graph of the equation.
-
A) (0, -7), (49, 0), (0, 7)
B) (-7, 0), (0, -49), (7, 0)
C) (7, 0), (0, 49), (0, -49)
D) (0, -7), (-49, 0), (0, 7)
-
A) (0, -7), (49, 0), (0, 7)
B) (-7, 0), (0, -49), (7, 0)
C) (7, 0), (0, 49), (0, -49)
D) (0, -7), (-49, 0), (0, 7)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
64
List the intercepts for the graph of the equation.
-
A) (-2, 0), (-5, 0), (0, 10)
B) (0, 2), (0, 5), (10, 0)
C) (0, -2), (0, -5), (10, 0)
D) (2, 0), (5, 0), (0, 10)
-
A) (-2, 0), (-5, 0), (0, 10)
B) (0, 2), (0, 5), (10, 0)
C) (0, -2), (0, -5), (10, 0)
D) (2, 0), (5, 0), (0, 10)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
65
List the intercepts for the graph of the equation.
-
A) (0, -7), (0, 0), (0, 7)
B) (-7, 0), (0, 0), (7, 0)
C) (-49, 0), (0, 0), (49, 0)
D) (0, 0)
-
A) (0, -7), (0, 0), (0, 7)
B) (-7, 0), (0, 0), (7, 0)
C) (-49, 0), (0, 0), (49, 0)
D) (0, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
66
List the intercepts for the graph of the equation.
-
A) (0, 25)
B) (0, 25), (-5, 0), (5, 0)
C) (25, 0)
D) (25, 0), (0, -5), (0, 5)
-
A) (0, 25)
B) (0, 25), (-5, 0), (5, 0)
C) (25, 0)
D) (25, 0), (0, -5), (0, 5)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
67
List the intercepts for the graph of the equation.
-
A) (0, 0)
B) (-3, 0), (3, 0)
C) (0, -3), (0, 3)
D) (-9, 0), (0, 0), (9, 0)
-
A) (0, 0)
B) (-3, 0), (3, 0)
C) (0, -3), (0, 3)
D) (-9, 0), (0, 0), (9, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
68
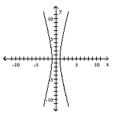
List the intercepts of the graph.Tell whether the graph is symmetric with respect to the x-axis, y-axis, origin, or none of
these.
-
A) intercepts: and
symmetric with respect to -axis
B) intercepts: and
symmetric with respect to -axis, -axis, and origin
C) intercepts: and
symmetric with respect to origin
D) intercepts: and
symmetric with respect to -axis, -axis, and origin
these.
-

A) intercepts: and
symmetric with respect to -axis
B) intercepts: and
symmetric with respect to -axis, -axis, and origin
C) intercepts: and
symmetric with respect to origin
D) intercepts: and
symmetric with respect to -axis, -axis, and origin

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
69
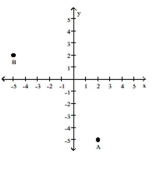
Plot the point A. Plot the point B that has the given symmetry with point A.
-A = (2, -5); B is symmetric to A with respect to the x-axis
A)
B)
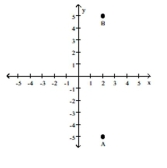
C)

D)
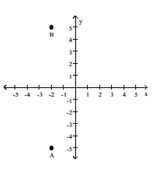
-A = (2, -5); B is symmetric to A with respect to the x-axis

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
70
List the intercepts of the graph.
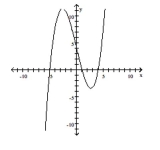
A) (4, 0), (0, 4), (0, 1), (0, -5)
B) (-4, 0), (1, 0), (5, 0), (0, 4)
C) (4, 0), (0, -4), (0, 1), (0, 5)
D) (4, 0), (1, 0) (-5, 0), (0, 4)

A) (4, 0), (0, 4), (0, 1), (0, -5)
B) (-4, 0), (1, 0), (5, 0), (0, 4)
C) (4, 0), (0, -4), (0, 1), (0, 5)
D) (4, 0), (1, 0) (-5, 0), (0, 4)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
71
List the intercepts for the graph of the equation.
-
A) (0, 1)
B) (0, 0)
C) (1, 1)
D) (1, 0)
-
A) (0, 1)
B) (0, 0)
C) (1, 1)
D) (1, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
72
List the intercepts of the graph.Tell whether the graph is symmetric with respect to the x-axis, y-axis, origin, or none of
these.
-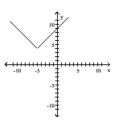
A) intercept:
symmetric with respect to -axis
B) intercept:
no symmetry
C) intercept:
no symmetry
D) intercept:
symmetric with respect to -axis
these.
-

A) intercept:
symmetric with respect to -axis
B) intercept:
no symmetry
C) intercept:
no symmetry
D) intercept:
symmetric with respect to -axis

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
73
List the intercepts for the graph of the equation.
-
A) (-16, 0), (0, -4), (0, 4), (16, 0)
B) (-4, 0), (-16, 0), (16, 0), (4, 0)
C) (-4, 0), (0, -2), (0, 2), (4, 0)
D) (-2, 0), (-4, 0), (4, 0), (2, 0)
-
A) (-16, 0), (0, -4), (0, 4), (16, 0)
B) (-4, 0), (-16, 0), (16, 0), (4, 0)
C) (-4, 0), (0, -2), (0, 2), (4, 0)
D) (-2, 0), (-4, 0), (4, 0), (2, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
74
List the intercepts for the graph of the equation.
y = x - 6
A) (6, 0), (0, -6)
B) (6, 0), (0, 6)
C) (-6, 0), (0, 6)
D) (-6, 0), (0, -6)
y = x - 6
A) (6, 0), (0, -6)
B) (6, 0), (0, 6)
C) (-6, 0), (0, 6)
D) (-6, 0), (0, -6)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
75
List the intercepts for the graph of the equation.
-
A) (0, 1), (-1, 0), (1, 0)
B) (0, -1)
C) (0, 1)
D) (0, -1), (-1, 0), (1, 0)
-
A) (0, 1), (-1, 0), (1, 0)
B) (0, -1)
C) (0, 1)
D) (0, -1), (-1, 0), (1, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
76
List the intercepts for the graph of the equation.
-
A) (0, -27), (3, 0)
B) (-27, 0), (0, 3)
C) (0, -3), (-3, 0)
D) (0, -3), (0, 3)
-
A) (0, -27), (3, 0)
B) (-27, 0), (0, 3)
C) (0, -3), (-3, 0)
D) (0, -3), (0, 3)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
77
List the intercepts for the graph of the equation.
-
A) (-9, 0), (0, -1), (0, 1), (9, 0)
B) (-1, 0), (0, -3), (0, 3), (1, 0)
C) (-1, 0), (0, -9), (0, 9), (1, 0)
D) (-3, 0), (0, -1), (0, 1), (3, 0)
-
A) (-9, 0), (0, -1), (0, 1), (9, 0)
B) (-1, 0), (0, -3), (0, 3), (1, 0)
C) (-1, 0), (0, -9), (0, 9), (1, 0)
D) (-3, 0), (0, -1), (0, 1), (3, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
78
List the intercepts for the graph of the equation.
-
A) (0, -5), (25, 0), (0, 5)
B) (-5, 0), (0, -25), (5, 0)
C) (5, 0), (0, 25), (0, -25)
D) (-5, 0), (0, 25), (5, 0)
-
A) (0, -5), (25, 0), (0, 5)
B) (-5, 0), (0, -25), (5, 0)
C) (5, 0), (0, 25), (0, -25)
D) (-5, 0), (0, 25), (5, 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
79
List the intercepts for the graph of the equation.
y = 2x
A) (2, 0)
B) (0, 0)
C) (0, 2)
D) (2, 2)
y = 2x
A) (2, 0)
B) (0, 0)
C) (0, 2)
D) (2, 2)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
80
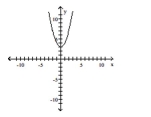
List the intercepts of the graph.Tell whether the graph is symmetric with respect to the x-axis, y-axis, origin, or none of
these.
-
A) intercept:
symmetric with respect to -axis
B) intercept:
symmetric with respect to -axis
C) intercept:
symmetric with respect to -axis
D) intercept:
symmetric with respect to origin
these.
-

A) intercept:
symmetric with respect to -axis
B) intercept:
symmetric with respect to -axis
C) intercept:
symmetric with respect to -axis
D) intercept:
symmetric with respect to origin

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck



