Deck 6: Discrete Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/76
Play
Full screen (f)
Deck 6: Discrete Probability Distributions
1
Determine whether the random variable described is discrete or continuous. The length in seconds of a randomly-selected TV commercial
A) discrete
B) continuous
A) discrete
B) continuous
continuous
2
The number of customers in a line at a supermarket express checkout counter is a random variable with the following probability distribution. 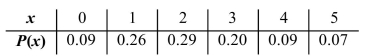 Find P(2 or fewer).
Find P(2 or fewer).
A) 0.65
B) 0.29
C) 0.35
D) 0.64
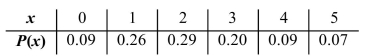 Find P(2 or fewer).
Find P(2 or fewer).A) 0.65
B) 0.29
C) 0.35
D) 0.64
0.64
3
Determine whether the table represents a discrete probability distribution. 
A) Yes
B) No

A) Yes
B) No
No
4
Determine whether the random variable described is discrete or continuous. The total value of a set of coins
A) discrete
B) continuous
A) discrete
B) continuous

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether the table represents a discrete probability distribution. 
A) Yes
B) No

A) Yes
B) No

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
6
Determine whether the table represents a discrete probability distribution. 
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
7
The following table presents the probability distribution of the number of vacations X taken last year for a randomly chosen family. Find P(1 or more). 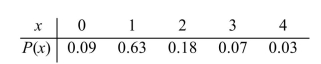
A) 0.63
B) 0.72
C) 0.28
D) 0.91
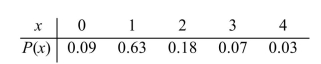
A) 0.63
B) 0.72
C) 0.28
D) 0.91

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
8
Fill in the missing value so that the following table represents a probability distribution. 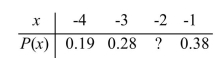
A) 0.25
B) 0.15
C) 0.09
D) 0
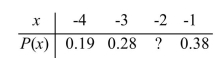
A) 0.25
B) 0.15
C) 0.09
D) 0

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
9
The number of customers in a line at a supermarket express checkout counter is a random variable with the following probability distribution. 
A) 2.12
B) 2.23
C) 4.48
D) 1.46

A) 2.12
B) 2.23
C) 4.48
D) 1.46

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
10
A sample of 6,000 computer monitors are examined for stuck pixels. Of them, 4,074 have no stuck pixels, 1,153 have one stuck pixel, 462 have two stuck pixels, 226 have three stuck pixels, and 85
Have four stuck pixels. Let X be the number of stuck pixels of a monitor randomly sampled from
This population. Find the probability distribution of X.
A)
B)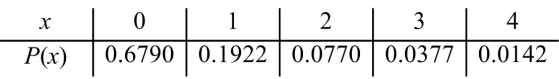
C)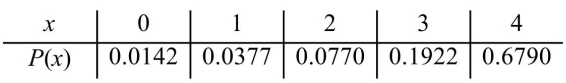
D)
Have four stuck pixels. Let X be the number of stuck pixels of a monitor randomly sampled from
This population. Find the probability distribution of X.
A)

B)
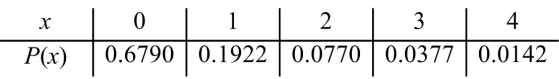
C)
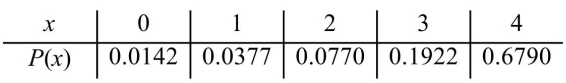
D)


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
11
The following table presents the probability distribution of the number of vacations X taken last year for a randomly chosen family. Compute the mean 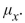
A) 1.37
B) 0.71
C) 1.43
D) 0.84
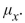
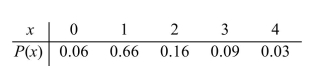
A) 1.37
B) 0.71
C) 1.43
D) 0.84

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether the random variable described is discrete or continuous. The number of 3-point shots made in a basketball game
A) discrete
B) continuous
A) discrete
B) continuous

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
13
The following table presents the probability distribution of the number of vacations X taken last year for a randomly chosen family. Compute the standard deviation 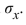
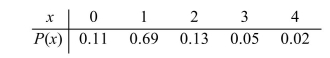
A) 1.18
B) 1.29
C) 0.59
D) 0.77
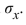
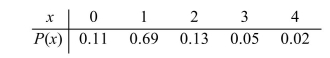
A) 1.18
B) 1.29
C) 0.59
D) 0.77

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
14
The number of customers in a line at a supermarket express checkout counter is a random variable with the following probability distribution. 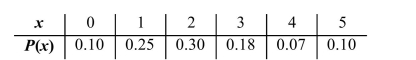 Compute the mean
Compute the mean 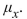
A) 0.36
B) 2.17
C) 0.17
D) 0.43
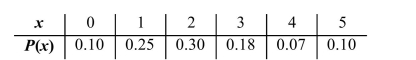 Compute the mean
Compute the mean 
A) 0.36
B) 2.17
C) 0.17
D) 0.43

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
15
The number of customers in a line at a supermarket express checkout counter is a random variable with the following probability distribution.  Find the probability that there are fewer than four people in line.
Find the probability that there are fewer than four people in line.
A) 0.18
B) 0.82
C) 0.11
D) 0.93
 Find the probability that there are fewer than four people in line.
Find the probability that there are fewer than four people in line.A) 0.18
B) 0.82
C) 0.11
D) 0.93

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
16
A survey asked 870 people how many times per week they dine out at a restaurant. The results are presented in the following table. 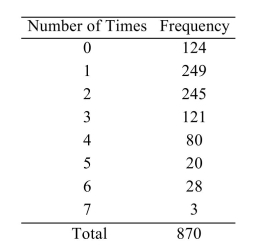 Consider the 870 people to be a population. Let X be the number of times per week a person dines out
Consider the 870 people to be a population. Let X be the number of times per week a person dines out
For a person sampled at random from this population. Find the probability that a person dines out 4
Or more times per week.
A) 0.849
B) 0.151
C) 0.059
D) 0.611
 Consider the 870 people to be a population. Let X be the number of times per week a person dines out
Consider the 870 people to be a population. Let X be the number of times per week a person dines outFor a person sampled at random from this population. Find the probability that a person dines out 4
Or more times per week.
A) 0.849
B) 0.151
C) 0.059
D) 0.611

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
17
The following table presents the probability distribution of the number of vacations X taken last year for a randomly chosen family. Find the probability that a family took at least 3 vacations last year. 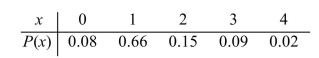
A) 0.11
B) 0.09
C) 0.26
D) 0.89
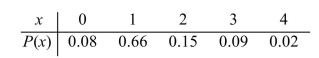
A) 0.11
B) 0.09
C) 0.26
D) 0.89

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether the random variable described is discrete or continuous. The number of minutes you must wait in line at the grocery store
A) continuous
B) discrete
A) continuous
B) discrete

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
19
Compute the mean of the random variable with the given discrete probability distribution. 
A) 11.0
B) 121.5
C) 21
D) 17.5

A) 11.0
B) 121.5
C) 21
D) 17.5

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
20
There are 4,000 undergraduates registered at a certain college. Of them, 364 are taking one course, 496 are taking two courses, 460 are taking three courses, 1,512 are taking four courses, 1,056 are
Taking five courses, and 112 are taking six courses. Let X be the number of courses taken by a
Student randomly sampled from this population. Find the probability distribution of X.
A)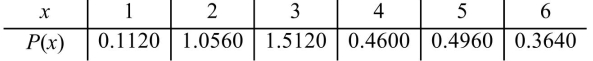
B)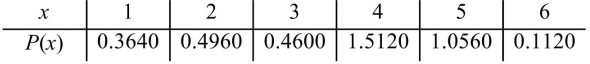
C)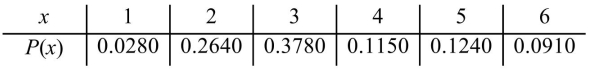
D)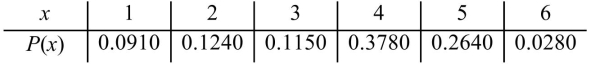
Taking five courses, and 112 are taking six courses. Let X be the number of courses taken by a
Student randomly sampled from this population. Find the probability distribution of X.
A)
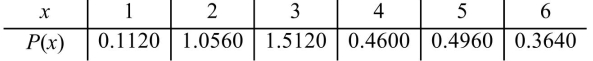
B)
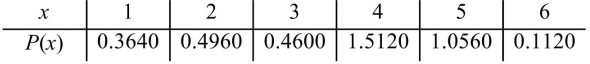
C)
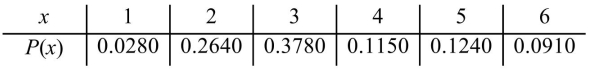
D)
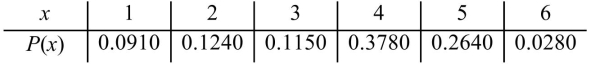

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
21
A survey asked 805 people how many times per week they dine out at a restaurant. The results are presented in the following table.  Consider the 805 people to be a population. Let X be the number of times per week a person dines out
Consider the 805 people to be a population. Let X be the number of times per week a person dines out
For a person sampled at random from this population. Compute the standard deviation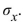
A) 2.1
B) 1.5
C) 2.2
D) 1.9
 Consider the 805 people to be a population. Let X be the number of times per week a person dines out
Consider the 805 people to be a population. Let X be the number of times per week a person dines outFor a person sampled at random from this population. Compute the standard deviation
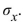
A) 2.1
B) 1.5
C) 2.2
D) 1.9

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
22
A student takes a true-false test that has 14 questions and guesses randomly at each answer. Let X be the number of questions answered correctly. Find P(5)
A) 0.1222
B) 0.0001
C) 0.1833
D) 0.0611
A) 0.1222
B) 0.0001
C) 0.1833
D) 0.0611

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
23
A coin is tossed 14 times. Let X be the number of heads obtained. Is this a binomial distribution, and if so, what is the number of trials?
A) Not binomial
B) Binomial, n = 14
C) Binomial, n = 2
A) Not binomial
B) Binomial, n = 14
C) Binomial, n = 2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
24
In the game of craps, two dice are rolled, and people bet on the outcome. For example, you can bet $1 that the dice will total 11. The probability that you win is 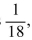 , and if you win, your profit is $15.
, and if you win, your profit is $15.
If you lose, you lose $1. What is the expected value of your profit?
A) $0.83
B) -$0.94
C) -$0.11
D) $0.11
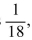 , and if you win, your profit is $15.
, and if you win, your profit is $15.If you lose, you lose $1. What is the expected value of your profit?
A) $0.83
B) -$0.94
C) -$0.11
D) $0.11

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
25
A coin is tossed until a head appears. Let X be the number of tosses. Is this a binomial distribution, and if so, what is the number of trials?
A) Not binomial
B) Binomial, n = X
C) Binomial, n = 2
A) Not binomial
B) Binomial, n = X
C) Binomial, n = 2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
26
A die is rolled 11 times. Let X be the sum of the numbers obtained. Is this a binomial distribution, and if so, what is the number of trials?
A) Not binomial
B) Binomial, n = 6
C) Binomial, n = 11
A) Not binomial
B) Binomial, n = 6
C) Binomial, n = 11

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
27
Determine the indicated probability for a binomial experiment with the given number of trials n and the given success probability p.
N = 15, p = 0.9, P(13 or more)
A) 0.9444
B) 0.5490
C) 0.1841
D) 0.8159
N = 15, p = 0.9, P(13 or more)
A) 0.9444
B) 0.5490
C) 0.1841
D) 0.8159

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
28
An investor is considering a $25,000 investment in a start-up company. She estimates that she has probability 0.15 of a $20,000 loss, probability 0.1 of a $30,000 profit, probability 0.25 of a $40,000
Profit, and probability 0.5 of breaking even (a profit of $0). What is the expected value of the profit?
A) $22,500
B) $10,000
C) $16,000
D) $16,667
Profit, and probability 0.5 of breaking even (a profit of $0). What is the expected value of the profit?
A) $22,500
B) $10,000
C) $16,000
D) $16,667

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
29
An insurance company sells a one-year term life insurance policy to an 80-year-old woman. The woman pays a premium of $1000. If she dies within one year, the company will pay $18,500 to her
Beneficiary. According to the company's statistics department, the probability that an 80-year-old
Woman will be alive one year later is 0.9581. Find the expected value of the insurance company's
Profit.
A) -$224.85
B) $224.85
C) -$182.95
D) $182.95
Beneficiary. According to the company's statistics department, the probability that an 80-year-old
Woman will be alive one year later is 0.9581. Find the expected value of the insurance company's
Profit.
A) -$224.85
B) $224.85
C) -$182.95
D) $182.95

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
30
In a lottery, you pay $1 and pick a number from 000 to 999. If your number comes up, you win $350, which is a profit of $349. If you lose, you lose $1. Your probability of winning is 0.001.
What is the expected value of your profit?
A) $0.349
B) -$0.65
C) $2.50
D) $0.65
What is the expected value of your profit?
A) $0.349
B) -$0.65
C) $2.50
D) $0.65

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
31
A survey asked 808 people how many times per week they dine out at a restaurant. The results are presented in the following table.  Consider the 808 people to be a population. Let X be the number of times per week a person dines out
Consider the 808 people to be a population. Let X be the number of times per week a person dines out
For a person sampled at random from this population. Find the probability that a person does not
Dine out at all.
A) 0
B) 0.144
C) 0.285
D) 0.428
 Consider the 808 people to be a population. Let X be the number of times per week a person dines out
Consider the 808 people to be a population. Let X be the number of times per week a person dines outFor a person sampled at random from this population. Find the probability that a person does not
Dine out at all.
A) 0
B) 0.144
C) 0.285
D) 0.428

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
32
An investor is considering a $25,000 investment in a start-up company. She estimates that she has probability 0.2 of a $15,000 loss, probability 0.15 of a $20,000 loss, probability 0.05 of a $40,000
Profit, and probability 0.6 of breaking even (a profit of $0). What is the expected value of the profit?
A) $11,000
B) $1,667
C) -$4,000
D) $8,000
Profit, and probability 0.6 of breaking even (a profit of $0). What is the expected value of the profit?
A) $11,000
B) $1,667
C) -$4,000
D) $8,000

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
33
Ten students are chosen from a statistics class of 22 students. Let X be the number who got an "A" in the class.
Is this a binomial distribution, and if so, what is the number of trials?
A) Not binomial
B) Binomial, n = 10
C) Binomial, n = 12
D) Binomial, n = 22
Is this a binomial distribution, and if so, what is the number of trials?
A) Not binomial
B) Binomial, n = 10
C) Binomial, n = 12
D) Binomial, n = 22

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
34
Determine the indicated probability for a binomial experiment with the given number of trials n and the given success probability p.
N = 15, p = 0.9, P(14)
A) 0.2288
B) 0.0000
C) 0.3432
D) 0.9000
N = 15, p = 0.9, P(14)
A) 0.2288
B) 0.0000
C) 0.3432
D) 0.9000

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
35
A student takes a true-false test that has 8 questions and guesses randomly at each answer. Let X be the number of questions answered correctly. Find P(6 or more)
A) 0.3633
B) 0.6367
C) 0.0352
D) 0.1445
A) 0.3633
B) 0.6367
C) 0.0352
D) 0.1445

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
36
Determine the indicated probability for a binomial experiment with the given number of trials n and the given success probability p.
N =8, p = 0.6, P(3 or fewer)
A) 0.8263
B) 0.0498
C) 0.1737
D) 0.4059
N =8, p = 0.6, P(3 or fewer)
A) 0.8263
B) 0.0498
C) 0.1737
D) 0.4059

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
37
Determine the indicated probability for a binomial experiment with the given number of trials n and the given success probability p.
N = 11, p = 0.7, P(Fewer than 4)
A) 0.9957
B) 0.0006
C) 0.0216
D) 0.0043
N = 11, p = 0.7, P(Fewer than 4)
A) 0.9957
B) 0.0006
C) 0.0216
D) 0.0043

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
38
A survey asked 818 people how many times per week they dine out at a restaurant. The results are presented in the following table.  Consider the 818 people to be a population. Let X be the number of times per week a person dines out
Consider the 818 people to be a population. Let X be the number of times per week a person dines out
For a person sampled at random from this population. Compute the mean
A) 1.5
B) 2.2
C) 2.3
D) 2.0
 Consider the 818 people to be a population. Let X be the number of times per week a person dines out
Consider the 818 people to be a population. Let X be the number of times per week a person dines outFor a person sampled at random from this population. Compute the mean

A) 1.5
B) 2.2
C) 2.3
D) 2.0

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
39
A student takes a true-false test that has 13 questions and guesses randomly at each answer. Let X be the number of questions answered correctly. Find P(Fewer than 4)
A) 0.8666
B) 0.1334
C) 0.0112
D) 0.0461
A) 0.8666
B) 0.1334
C) 0.0112
D) 0.0461

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
40
The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 40% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 12 adult dogs is studied.
What is the probability that exactly 3 of them weigh 65 lb or more?
A) 0.0125
B) 0.1419
C) 0.8581
D) 0.9875
What is the probability that exactly 3 of them weigh 65 lb or more?
A) 0.0125
B) 0.1419
C) 0.8581
D) 0.9875

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
41
At an airport, 77% of recent flights have arrived on time. A sample of 11 flights is studied. What is the mean number of flights that are on time?
A) 1.95
B) 8.47
C) 2.53
D) 2.91
A) 1.95
B) 8.47
C) 2.53
D) 2.91

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
42
It is estimated that 30% of households own a riding lawn mower. A sample of 18 households is studied. What is the probability that no more than 3 of these own a riding lawn mower?
A) 0.94
B) 0.1646
C) 0.8354
D) 0.0600
A) 0.94
B) 0.1646
C) 0.8354
D) 0.0600

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
43
It is estimated that 45% of households own a riding lawn mower. A sample of 15 households is studied. What is the probability that exactly 7 of these own a riding lawn mower?
A) 0.8353
B) 0.1647
C) 0.7987
D) 0.2013
A) 0.8353
B) 0.1647
C) 0.7987
D) 0.2013

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
44
At an airport, 83% of recent flights have arrived on time. A sample of 12 flights is studied. What is the standard deviation of the number of flights that are on time?
A) 1.69
B) 9.96
C) 1.30
D) 0.38
A) 1.69
B) 9.96
C) 1.30
D) 0.38

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
45
In a poll conducted by a survey firm, 75% of respondents said that their jobs were sometimes or always stressful. Nine workers are chosen at random. What is the probability that less than 4 of
Them find their jobs stressful?
A) 0.0100
B) 0.9900
C) 0.0489
D) 0.0389
Them find their jobs stressful?
A) 0.0100
B) 0.9900
C) 0.0489
D) 0.0389

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
46
In a poll conducted by a survey firm, 73% of respondents said that their jobs were sometimes or always stressful. Eight workers are chosen at random. What is the mean number of workers who
Find their job stressful?
A) 5.84
B) 1.58
C) 1.26
D) 2.16
Find their job stressful?
A) 5.84
B) 1.58
C) 1.26
D) 2.16

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
47
In a poll conducted by a survey firm, 82% of respondents said that their jobs were sometimes or always stressful. Eleven workers are chosen at random. What is the probability that more than 9 of
Them find their jobs stressful?
A) 0.3164
B) 0.3849
C) 0.6836
D) 0.6151
Them find their jobs stressful?
A) 0.3164
B) 0.3849
C) 0.6836
D) 0.6151

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
48
The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 45% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 16 adult dogs is studied.
What is the probability that no more than 3 of them weigh 65 lb or more?
A) 0.9719
B) 0.9934
C) 0.0066
D) 0.0281
What is the probability that no more than 3 of them weigh 65 lb or more?
A) 0.9719
B) 0.9934
C) 0.0066
D) 0.0281

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
49
The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 25% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 11 adult dogs is studied.
What is the mean number of dogs who weigh 65 lb or more?
A) 11
B) 2.0625
C) 2.75
D) 1.4361
What is the mean number of dogs who weigh 65 lb or more?
A) 11
B) 2.0625
C) 2.75
D) 1.4361

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
50
It is estimated that 40% of households own a riding lawn mower. A sample of 13 households is studied. What is the mean number of households who own a riding mower?
A) 3.12
B) 13
C) 1.7664
D) 5.2
A) 3.12
B) 13
C) 1.7664
D) 5.2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
51
The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 45% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 12 adult dogs is studied.
What is the probability that more than 9 of them weigh 65 lb or more?
A) 0.0079
B) 0.9644
C) 0.0356
D) 0.0011
What is the probability that more than 9 of them weigh 65 lb or more?
A) 0.0079
B) 0.9644
C) 0.0356
D) 0.0011

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
52
At an airport, 78% of recent flights have arrived on time. A sample of 11 flights is studied. Find the probability that exactly 7 of them were on time.
A) 0.1358
B) 0.0014
C) 0.8642
D) 0.0030
A) 0.1358
B) 0.0014
C) 0.8642
D) 0.0030

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
53
Determine the indicated probability for a Poisson random variable with the given values of 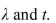
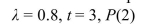
A) 0.0431
B) 0.2613
C) 0.9569
D) 0.3840
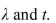
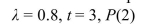
A) 0.0431
B) 0.2613
C) 0.9569
D) 0.3840

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
54
In a poll conducted by a survey firm, 76% of respondents said that their jobs were sometimes or always stressful. Eight workers are chosen at random. What is the standard deviation of the
Number of workers who find their jobs stressful?
A) 1.21
B) 0.43
C) 1.46
D) 2.47
Number of workers who find their jobs stressful?
A) 1.21
B) 0.43
C) 1.46
D) 2.47

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
55
The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 25% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 14 adult dogs is studied.
What is the standard deviation of the number of dogs who weigh 65 lb or more?
A) 3.5
B) 14
C) 1.6202
D) 2.625
What is the standard deviation of the number of dogs who weigh 65 lb or more?
A) 3.5
B) 14
C) 1.6202
D) 2.625

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
56
At an airport, 78% of recent flights have arrived on time. A sample of 14 flights is studied. Find the probability that more than 12 of them were on time.
A) 0.3761
B) 0.6239
C) 0.1527
D) 0.8473
A) 0.3761
B) 0.6239
C) 0.1527
D) 0.8473

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
57
At an airport, 77% of recent flights have arrived on time. A sample of 11 flights is studied. Find the probability that no more than 4 of them were on time.
A) 0.0039
B) 0.0046
C) 0.9954
D) 0.9961
A) 0.0039
B) 0.0046
C) 0.9954
D) 0.9961

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
58
It is estimated that 35% of households own a riding lawn mower. A sample of 10 households is studied. What is the standard deviation of the number of households who own a riding lawn mower?
A) 3.5
B) 1.5083
C) 2.275
D) 10
A) 3.5
B) 1.5083
C) 2.275
D) 10

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
59
In a poll conducted by a survey firm, 84% of respondents said that their jobs were sometimes or always stressful. Ten workers are chosen at random. What is the probability that exactly 6 of them
Find their jobs stressful?
A) 0.0018
B) 0.0483
C) 0.9517
D) 0.0012
Find their jobs stressful?
A) 0.0018
B) 0.0483
C) 0.9517
D) 0.0012

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
60
It is estimated that 40% of households own a riding lawn mower. A sample of 13 households is studied. What is the probability that more than 10 of these own a riding lawn mower?
A) 0.0078
B) 0.9922
C) 0.0013
D) 0.0001
A) 0.0078
B) 0.9922
C) 0.0013
D) 0.0001

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
61
Determine the indicated probability for a Poisson random variable with the given values of 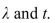

A) 0.6469
B) 0.7141
C) 0.4936
D) 0.5064
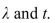

A) 0.6469
B) 0.7141
C) 0.4936
D) 0.5064

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
62
The number of typographical errors in a document follows a Poisson distribution with a mean of 4 errors per page. Let X represent the number of errors on 2 pages. Find 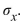
A) 3.8
B) 2.8
C) 8
D) 4
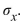
A) 3.8
B) 2.8
C) 8
D) 4

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
63
Determine the indicated probability for a Poisson random variable with the given values of 
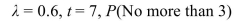
A) 0.3954
B) 0.6196
C) 0.3804
D) 0.2102

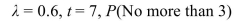
A) 0.3954
B) 0.6196
C) 0.3804
D) 0.2102

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
64
The number of typographical errors in a document follows a Poisson distribution with a mean of 2 errors per page. Let X represent the number of errors on 3 pages. Find P(Less than 3).
A) 0.0620
B) 0.0174
C) 0.6767
D) 0.0595
A) 0.0620
B) 0.0174
C) 0.6767
D) 0.0595

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
65
An environmental scientist obtains a sample of water from an irrigation canal that contains a certain type of bacteria at a concentration of 4 per milliliter. What is the probability that there will be
Exactly 8 bacteria in a 4-milliliter sample?
A) 0.0298
B) 0.0120
C) 0.0060
D) 0.9940
Exactly 8 bacteria in a 4-milliliter sample?
A) 0.0298
B) 0.0120
C) 0.0060
D) 0.9940

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
66
An environmental scientist obtains a sample of water from an irrigation canal that contains a certain type of bacteria at a concentration of 2 per milliliter. Find the standard deviation of the number of
Bacteria in a 4-milliliter sample.
A) 8
B) 1.4
C) 2.8
D) 2
Bacteria in a 4-milliliter sample.
A) 8
B) 1.4
C) 2.8
D) 2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
67
The number of typographical errors in a document follows a Poisson distribution with a mean of 2 errors per page. Let X represent the number of errors on 4 pages. Find P(5).
A) 0.1221
B) 0.0916
C) 0.9639
D) 0.0361
A) 0.1221
B) 0.0916
C) 0.9639
D) 0.0361

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
68
The number of typographical errors in a document follows a Poisson distribution with a mean of 4 errors per page. Let X represent the number of errors on 2 pages. Find 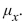
A) 4
B) 9
C) 8
D) 2.8
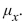
A) 4
B) 9
C) 8
D) 2.8

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
69
The number of typographical errors in a document follows a Poisson distribution with a mean of 2 errors per page. Let X represent the number of errors on 4 pages. Find P(Greater than 1).
A) 0.5940
B) 0.9862
C) 0.9970
D) 0.9997
A) 0.5940
B) 0.9862
C) 0.9970
D) 0.9997

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
70
Last year, a manufacturer produced 200,000 DVD players. Of these, approximately 2% were defective. Assume that a simple random sample of n = 130 players is drawn. Use the Poisson
Approximation to the binomial distribution to compute the mean number of DVD players that were
Defective.
A) 2.6
B) 25.1
C) 2
D) 1.6
Approximation to the binomial distribution to compute the mean number of DVD players that were
Defective.
A) 2.6
B) 25.1
C) 2
D) 1.6

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
71
Last year, a manufacturer produced 1,950,000 DVD players. Of these, approximately 5% were defective. Assume that a simple random sample of n = 230 players is drawn. Use the Poisson
Approximation to the binomial distribution to compute the probability that exactly nineteen of the
230 DVD players were defective.
A) 0.0119
B) 0.0826
C) 0.0068
D) 0.0196
Approximation to the binomial distribution to compute the probability that exactly nineteen of the
230 DVD players were defective.
A) 0.0119
B) 0.0826
C) 0.0068
D) 0.0196

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
72
An environmental scientist obtains a sample of water from an irrigation canal that contains a certain type of bacteria at a concentration of 6 per milliliter. Find the mean number of bacteria in a
8-milliliter sample.
A) 2.4
B) 48
C) 6.9
D) 6
8-milliliter sample.
A) 2.4
B) 48
C) 6.9
D) 6

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
73
Last year, a manufacturer produced 350,000 DVD players. Of these, approximately 1% were defective. Assume that a simple random sample of n = 140 players is drawn. Use the Poisson
Approximation to the binomial distribution to compute the standard deviation of the number of DVD
Players that were defective.
A) 1
B) 1.4
C) 48.3
D) 1.2
Approximation to the binomial distribution to compute the standard deviation of the number of DVD
Players that were defective.
A) 1
B) 1.4
C) 48.3
D) 1.2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
74
Determine the indicated probability for a Poisson random variable with the given values of 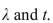
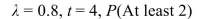
A) 0.9592
B) 0.0408
C) 0.8288
D) 0.6201
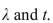
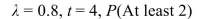
A) 0.9592
B) 0.0408
C) 0.8288
D) 0.6201

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
75
Last year, a manufacturer produced 1,950,000 DVD players. Of these, approximately 4% were defective. Assume that a simple random sample of n = 180 players is drawn. Use the Poisson
Approximation to the binomial distribution to compute the probability that fewer than four of the
180 DVD players were defective.
A) 0.0464
B) 0.0255
C) 0.0719
D) 0.0712
Approximation to the binomial distribution to compute the probability that fewer than four of the
180 DVD players were defective.
A) 0.0464
B) 0.0255
C) 0.0719
D) 0.0712

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
76
Determine the indicated probability for a Poisson random variable with the given values of 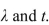
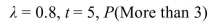
A) 0.4335
B) 0.4152
C) 0.5665
D) 0.2381
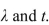
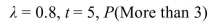
A) 0.4335
B) 0.4152
C) 0.5665
D) 0.2381

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck



