Deck 9: Inferences From Two Samples
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/192
Play
Full screen (f)
Deck 9: Inferences From Two Samples
1

B
2

 Find the critical values
Find the critical values 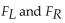 for a two-tailed hypothesis test based on the following values:
for a two-tailed hypothesis test based on the following values: 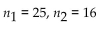
A) 0.5327, 2.2878
B) 0.4745, 2.4371
C) 0.7351, 2.2378
D) 0.4745, 2.2878
D
3
Express the alternative hypothesis in symbolic form. A professor claims that the mean amount of time (in hours) sophomores spent studying for the statistics final exam is more than that of freshmen. Assume that the two
Samples are independent. Let the freshmen be the first population and the sophomores be the second
Population.
Samples are independent. Let the freshmen be the first population and the sophomores be the second
Population.

C
4


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
5
If the heights of male college basketball players and female basketball players are used to construct a 95% confidence interval for the difference between the two population means, the result is 15.35 cm < 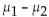 <
<
19)81 cm, where heights of male players correspond to population 1 and heights of female players correspond to
Population 2. Express the confidence interval with heights of female basketball players being population 1 and
Heights of male basketball players being population 2.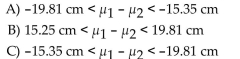
D) This cannot be determined without having the original data values.
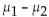 <
<19)81 cm, where heights of male players correspond to population 1 and heights of female players correspond to
Population 2. Express the confidence interval with heights of female basketball players being population 1 and
Heights of male basketball players being population 2.
D) This cannot be determined without having the original data values.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
6
Which distribution is used to test the claim that the standard deviation of the ages (in years) of when girls first learn to ride a bike is equal to the standard deviation of the ages (in years) when boys first lean to ride a bike?
A) F
B) chi-square
C) t
D) Normal
A) F
B) chi-square
C) t
D) Normal

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
7
Assume that two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. Which distribution is used to
Test the claim that women have a higher mean resting heart rate than men?
A) Normal
B) F
C) t
D) chi-square
Test the claim that women have a higher mean resting heart rate than men?
A) Normal
B) F
C) t
D) chi-square

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
8
Find sd. The differences between two sets of dependent data are 0.4, 0.24, 0.22, 0.26, 0.34. Round to the nearest hundredth.
A) 0.04
B) 0.24
C) 0.12
D) 0.08
A) 0.04
B) 0.24
C) 0.12
D) 0.08

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
9
Construct the indicated confidence interval for the difference between the two population means. Assume that the two samples are independent simple random samples selected from normally distributed populations. Do
Not assume that the population standard deviations are equal. A paint manufacturer wished to compare the
Drying times of two different types of paint. Independent simple random samples of 11 cans of type A and 9
Cans of type B were selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.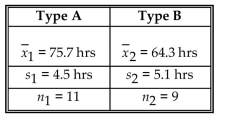 Construct a 98% confidence interval for
Construct a 98% confidence interval for 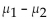 , the difference between the mean drying time for paint of type A
, the difference between the mean drying time for paint of type A
And the mean drying time for paint of type B.
Not assume that the population standard deviations are equal. A paint manufacturer wished to compare the
Drying times of two different types of paint. Independent simple random samples of 11 cans of type A and 9
Cans of type B were selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.
 Construct a 98% confidence interval for
Construct a 98% confidence interval for 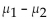 , the difference between the mean drying time for paint of type A
, the difference between the mean drying time for paint of type AAnd the mean drying time for paint of type B.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
10
Assume that you plan to use a significance level of α = 0.05 to test the claim that p1 = p2. Use the given sample sizes and numbers of successes to find the pooled estimate 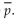 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth. 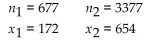
A) 0.408
B) 0.163
C) 0.204
D) 0.452
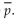 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth. 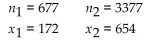
A) 0.408
B) 0.163
C) 0.204
D) 0.452

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
11
Determine whether the samples are independent or dependent. The effectiveness of a headache medicine is tested by measuring the intensity of a headache in patients before and after drug treatment. The data consist of
Before and after intensities for each patient.
A) Dependent samples
B) Independent samples
Before and after intensities for each patient.
A) Dependent samples
B) Independent samples

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
12
Determine the decision criterion for rejecting the null hypothesis in the given hypothesis test; i.e., describe the values of the test statistic that would result in rejection of the null hypothesis. Suppose you wish to test the
Claim that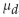 , the mean value of the differences d for a population of paired data, is greater than 0. Given a
, the mean value of the differences d for a population of paired data, is greater than 0. Given a
Sample of n = 15 and a significance level of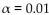 1, what criterion would be used for rejecting the null
1, what criterion would be used for rejecting the null
Hypothesis?
A) Reject null hypothesis if test statistic > 2.624.
B) Reject null hypothesis if test statistic < 2.624.
C) Reject null hypothesis if test statistic > 2.602.
D) Reject null hypothesis if test statistic > 2.977 or < -2.977.
Claim that
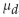 , the mean value of the differences d for a population of paired data, is greater than 0. Given a
, the mean value of the differences d for a population of paired data, is greater than 0. Given aSample of n = 15 and a significance level of
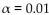 1, what criterion would be used for rejecting the null
1, what criterion would be used for rejecting the nullHypothesis?
A) Reject null hypothesis if test statistic > 2.624.
B) Reject null hypothesis if test statistic < 2.624.
C) Reject null hypothesis if test statistic > 2.602.
D) Reject null hypothesis if test statistic > 2.977 or < -2.977.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
13
Find 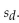 . Consider the set of differences between two dependent sets: 84, 85, 83, 63, 61, 100, 98. Round to the nearest tenth.
. Consider the set of differences between two dependent sets: 84, 85, 83, 63, 61, 100, 98. Round to the nearest tenth.
A) 13.1
B) 16.2
C) 15.7
D) 15.3
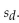 . Consider the set of differences between two dependent sets: 84, 85, 83, 63, 61, 100, 98. Round to the nearest tenth.
. Consider the set of differences between two dependent sets: 84, 85, 83, 63, 61, 100, 98. Round to the nearest tenth.A) 13.1
B) 16.2
C) 15.7
D) 15.3

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
14
The two data sets are dependent. Find 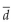 to the nearest tenth.
to the nearest tenth. 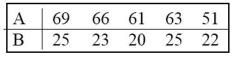
A) 39.0
B) 23.4
C) 50.7
D) 48.8
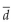 to the nearest tenth.
to the nearest tenth. 
A) 39.0
B) 23.4
C) 50.7
D) 48.8

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
15
Assume that you plan to use a significance level of  test the claim that
test the claim that  . Use the given sample sizes and numbers of successes to find the P-value for the hypothesis test.
. Use the given sample sizes and numbers of successes to find the P-value for the hypothesis test. 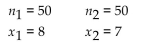
A) 0.7794
B) 0.6103
C) 0.2206
D) 0.3897
 test the claim that
test the claim that  . Use the given sample sizes and numbers of successes to find the P-value for the hypothesis test.
. Use the given sample sizes and numbers of successes to find the P-value for the hypothesis test. 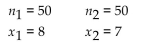
A) 0.7794
B) 0.6103
C) 0.2206
D) 0.3897

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
16
Assume that you plan to use a significance level of  05 to test the claim that
05 to test the claim that  . Use the given sample sizes and numbers of successes to find the pooled estimate
. Use the given sample sizes and numbers of successes to find the pooled estimate 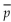 Round your answer to the nearest thousandth.
Round your answer to the nearest thousandth. 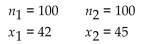
A) 0.305
B) 0.435
C) 0.479
D) 0.392
 05 to test the claim that
05 to test the claim that  . Use the given sample sizes and numbers of successes to find the pooled estimate
. Use the given sample sizes and numbers of successes to find the pooled estimate 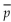 Round your answer to the nearest thousandth.
Round your answer to the nearest thousandth. 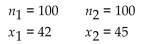
A) 0.305
B) 0.435
C) 0.479
D) 0.392

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
17
Assume that the following confidence interval for the difference in the mean length of male (sample 1) and female babies (sample 2) at birth was constructed using independent simple random samples. -0.2 in < 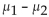 < 1.7 in. What does the confidence interval suggest about the difference in length between male babies and
< 1.7 in. What does the confidence interval suggest about the difference in length between male babies and
Female babies?
A) Male babies are longer.
B) Female babies are longer.
C) There is no difference in the length between male and female babies.
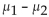 < 1.7 in. What does the confidence interval suggest about the difference in length between male babies and
< 1.7 in. What does the confidence interval suggest about the difference in length between male babies andFemale babies?
A) Male babies are longer.
B) Female babies are longer.
C) There is no difference in the length between male and female babies.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether the following statement regarding the hypothesis test for two population proportions is true or false:
However small the difference between two population proportions, for sufficiently large sample sizes, the null
Hypothesis of equal population proportions is likely to be rejected.
A) True
B) False
However small the difference between two population proportions, for sufficiently large sample sizes, the null
Hypothesis of equal population proportions is likely to be rejected.
A) True
B) False

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
19
When testing the claim that  , a test statistic of
, a test statistic of 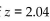 2.04 is obtained. Find the P-value obtained from this test statistic.
2.04 is obtained. Find the P-value obtained from this test statistic.
A) 0.0414
B) 0.9586
C) 0.0207
D) 0.9793
 , a test statistic of
, a test statistic of 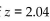 2.04 is obtained. Find the P-value obtained from this test statistic.
2.04 is obtained. Find the P-value obtained from this test statistic.A) 0.0414
B) 0.9586
C) 0.0207
D) 0.9793

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
20
Assume that you want to test the claim that the paired sample data come from a population for which the mean difference is 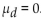 0. Compute the value of the t test statistic. Round intermediate calculations to four decimal
0. Compute the value of the t test statistic. Round intermediate calculations to four decimal
Places as needed and final answers to three decimal places as needed.
A) t = -0.690
B) t = -1.185
C) t = -1.480
D) t = -0.523
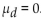 0. Compute the value of the t test statistic. Round intermediate calculations to four decimal
0. Compute the value of the t test statistic. Round intermediate calculations to four decimalPlaces as needed and final answers to three decimal places as needed.

A) t = -0.690
B) t = -1.185
C) t = -1.480
D) t = -0.523

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
21
Construct a confidence interval for 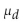 the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. Using the sample paired data below, construct
the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. Using the sample paired data below, construct
A 90% confidence interval for the population mean of all differences.

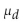 the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. Using the sample paired data below, construct
the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. Using the sample paired data below, constructA 90% confidence interval for the population mean of all differences.



Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
22
Find the number of successes x suggested by the given statement. A computer manufacturer randomly selects 2680 of its computers for quality assurance and finds that 1.98% of these computers are found to be defective.
A) 51
B) 53
C) 58
D) 56
A) 51
B) 53
C) 58
D) 56

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
23
Determine whether the samples are dependent or independent. The effectiveness of a headache medicine is tested by measuring the intensity of a headache in patients before and after drug treatment. The data consist of
Before and after intensities for each patient.
A) Independent samples
B) Dependent samples
Before and after intensities for each patient.
A) Independent samples
B) Dependent samples

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
24
Assume that two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. Which distribution is used to
Test the claim that mothers spend more time (in minutes) driving their kids to activities than fathers do?
A) F
B) t
C) chi-square
D) Normal
Test the claim that mothers spend more time (in minutes) driving their kids to activities than fathers do?
A) F
B) t
C) chi-square
D) Normal

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
25
A paint manufacturer made a modification to a paint to speed up its drying time. Independent simple random samples of 11 cans of type A (the original paint) and 9 cans of type B (the modified paint) were selected and
Applied to similar surfaces. The drying times, in hours, were recorded. The summary statistics are as follows.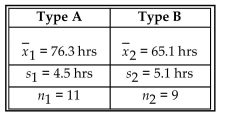 The following 98% confidence interval was obtained for
The following 98% confidence interval was obtained for 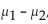 the difference between the mean drying time for paint
the difference between the mean drying time for paint
Cans of type A and the mean drying time for paint cans of type B: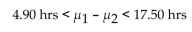 What does the confidence interval suggest about the population means?
What does the confidence interval suggest about the population means?
A) The confidence interval includes only positive values which suggests that the mean drying time for paint type A is smaller than the mean drying time for paint type B. The modification does not seem to be
Effective in reducing drying times.
B) The confidence interval includes 0 which suggests that the two population means might be equal. There doesn't appear to be a significant difference between the mean drying time for paint type A and the mean
Drying time for paint type B. The modification does not seem to be effective in reducing drying times.
C) The confidence interval includes only positive values which suggests that the mean drying time for paint type A is greater than the mean drying time for paint type B. The modification seems to be effective in
Reducing drying times.
D) The confidence interval includes only positive values which suggests that the two population means might be equal. There doesn't appear to be a significant difference between the mean drying time for paint
Type A and the mean drying time for paint type B. The modification does not seem to be effective in
Reducing drying times.
Applied to similar surfaces. The drying times, in hours, were recorded. The summary statistics are as follows.
 The following 98% confidence interval was obtained for
The following 98% confidence interval was obtained for 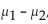 the difference between the mean drying time for paint
the difference between the mean drying time for paintCans of type A and the mean drying time for paint cans of type B:
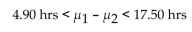 What does the confidence interval suggest about the population means?
What does the confidence interval suggest about the population means?A) The confidence interval includes only positive values which suggests that the mean drying time for paint type A is smaller than the mean drying time for paint type B. The modification does not seem to be
Effective in reducing drying times.
B) The confidence interval includes 0 which suggests that the two population means might be equal. There doesn't appear to be a significant difference between the mean drying time for paint type A and the mean
Drying time for paint type B. The modification does not seem to be effective in reducing drying times.
C) The confidence interval includes only positive values which suggests that the mean drying time for paint type A is greater than the mean drying time for paint type B. The modification seems to be effective in
Reducing drying times.
D) The confidence interval includes only positive values which suggests that the two population means might be equal. There doesn't appear to be a significant difference between the mean drying time for paint
Type A and the mean drying time for paint type B. The modification does not seem to be effective in
Reducing drying times.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
26
Assume that you want to test the claim that the paired sample data come from a population for which the mean difference is  Compute the value of the t test statistics. Round intermediate calculations to four decimal
Compute the value of the t test statistics. Round intermediate calculations to four decimal
Places as needed and final answers to three decimal places as needed.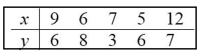
A) t = 0.415
B) t = 1.292
C) t = 0.578
D) t = 2.890
 Compute the value of the t test statistics. Round intermediate calculations to four decimal
Compute the value of the t test statistics. Round intermediate calculations to four decimalPlaces as needed and final answers to three decimal places as needed.

A) t = 0.415
B) t = 1.292
C) t = 0.578
D) t = 2.890

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
27
Construct the indicated confidence interval for the difference between the two population means. Assume that the two samples are independent simple random samples selected from normally distributed populations. Do
Not assume that the population standard deviations are equal. A paint manufacturer wished to compare the
Drying times of two different types of paint. Independent simple random samples of 11 cans of type A and 9
Cans of type B were selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.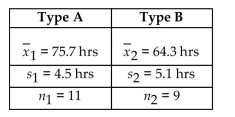
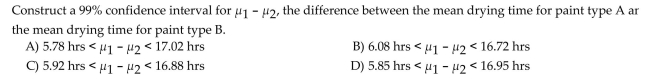
Not assume that the population standard deviations are equal. A paint manufacturer wished to compare the
Drying times of two different types of paint. Independent simple random samples of 11 cans of type A and 9
Cans of type B were selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.

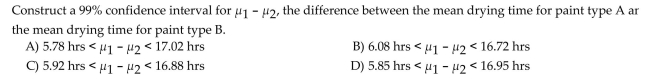

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
28
Assume that the following confidence interval for the difference in the mean time (in minutes) for male students to complete a statistics test (sample 1) and the mean time for female students to complete a statistics test (sample2) was constructed using independent simple random samples. 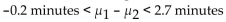 What does
What does
The confidence interval suggest about the difference in length between male and female test completion times?
A) Male students take longer to complete a statistics test.
B) Female students take longer to complete a statistics test.
C) There is no difference in the length of time for statistics test completion between male and female students.
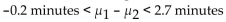 What does
What doesThe confidence interval suggest about the difference in length between male and female test completion times?
A) Male students take longer to complete a statistics test.
B) Female students take longer to complete a statistics test.
C) There is no difference in the length of time for statistics test completion between male and female students.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
29


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
30
A test of abstract reasoning is given to a random sample of students before and after they completed a formal logic course. The results are given below. Construct a 95% confidence interval for the mean difference between
The before and after scores.

The before and after scores.



Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
31
Express the alternative hypothesis in symbolic form. An automobile technician claims that the mean amount of time (in hours) per domestic car repair is more than that of foreign cars. Assume that two samples are
Independent. Let the domestic car repair times be the first population and the foreign car repair times be the
Second population.
Independent. Let the domestic car repair times be the first population and the foreign car repair times be the
Second population.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
32


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
33
Construct a confidence interval for µd the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. A test of writing ability is given to a random
Sample of students before and after they completed a formal writing course. The results are given below.
Construct a 99% confidence interval for the mean difference between the before and after scores.
Sample of students before and after they completed a formal writing course. The results are given below.
Construct a 99% confidence interval for the mean difference between the before and after scores.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
34
Which distribution is used to test the claim that the standard deviation of the lengths (in cm) of male babies at birth is equal to the standard deviation of the lengths (in cm) of female babies at birth?
A) Normal
B) chi-square
C) F
D) t
A) Normal
B) chi-square
C) F
D) t

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
35


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
36


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
37
Determine whether the samples are dependent or independent. The effectiveness of a new headache medicine is tested by measuring the amount of time before the headache is cured for patients who use the medicine and
Another group of patients who use a placebo drug.
A) Independent samples
B) Dependent samples
Another group of patients who use a placebo drug.
A) Independent samples
B) Dependent samples

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
38
Assume that you want to test the claim that the paired sample data come from a population for which the mean difference is 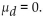 Compute the value of the t test statistic. Round intermediate calculations to four decimal
Compute the value of the t test statistic. Round intermediate calculations to four decimal
Places as needed and final answers to three decimal places as needed.
A) 9.468
B) 3.156
C) 1.052
D) 0.351
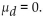 Compute the value of the t test statistic. Round intermediate calculations to four decimal
Compute the value of the t test statistic. Round intermediate calculations to four decimalPlaces as needed and final answers to three decimal places as needed.

A) 9.468
B) 3.156
C) 1.052
D) 0.351

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
39
Construct the indicated confidence interval for the difference between the two population means. Assume that the two samples are independent simple random samples selected from normally distributed populations. Also
Assume that the population standard deviations are equal ( ), so that the standard error of the difference
), so that the standard error of the difference
Between means is obtained by pooling the sample variances. A paint manufacturer wanted to compare the
Drying times of two different types of paint. Independent simple random samples of 11 cans of type A and 9
Cans of type B were selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.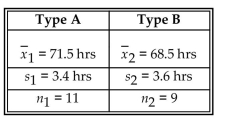
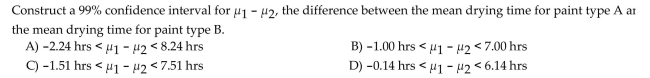
Assume that the population standard deviations are equal (
 ), so that the standard error of the difference
), so that the standard error of the differenceBetween means is obtained by pooling the sample variances. A paint manufacturer wanted to compare the
Drying times of two different types of paint. Independent simple random samples of 11 cans of type A and 9
Cans of type B were selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.

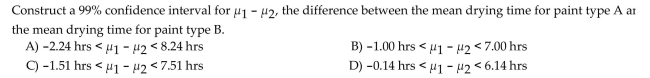

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
40
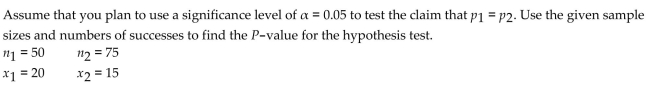
A) 0.0001
B) 0.1201
C) 0.0146
D) 0.0032

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
41
Test the indicated claim about the means of two populations. Assume that the two samples are independent
simple random samples selected from normally distributed populations. Do not assume that the population
standard deviations are equal. Use a 0.05 significance level to test the claim that the mean amount of time spent watching television by women is
Use a 0.05 significance level to test the claim that the mean amount of time spent watching television by women is
smaller than the mean amount of time spent watching television by men. Include your null and alternative hypotheses,
the test statistic, P-value or critical value(s), conclusion about the null hypothesis, and conclusion about the claim
in your answer.
simple random samples selected from normally distributed populations. Do not assume that the population
standard deviations are equal.
 Use a 0.05 significance level to test the claim that the mean amount of time spent watching television by women is
Use a 0.05 significance level to test the claim that the mean amount of time spent watching television by women issmaller than the mean amount of time spent watching television by men. Include your null and alternative hypotheses,
the test statistic, P-value or critical value(s), conclusion about the null hypothesis, and conclusion about the claim
in your answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
42
Test the given claim about the means of two populations. Assume that two dependent samples have been
randomly selected from normally distributed populations.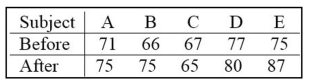 Using a 0.01 level of significance, test the claim that the tutoring has an effect on the math scores. Include your null and
Using a 0.01 level of significance, test the claim that the tutoring has an effect on the math scores. Include your null and
alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null hypothesis, and
conclusion about the claim in your answer.
randomly selected from normally distributed populations.
 Using a 0.01 level of significance, test the claim that the tutoring has an effect on the math scores. Include your null and
Using a 0.01 level of significance, test the claim that the tutoring has an effect on the math scores. Include your null andalternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null hypothesis, and
conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
43
Suppose you wish to test a claim about the mean of the differences from dependent samples or to construct a
confidence interval estimate of the mean of the differences from dependent samples. What are the
requirements?
confidence interval estimate of the mean of the differences from dependent samples. What are the
requirements?

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
44
To test the null hypothesis that the difference between two population proportions is equal to a nonzero
constant c, use the test statistic: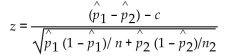 As long as
As long as  are both large, the sampling distribution of the test statistic z will be approximately the
are both large, the sampling distribution of the test statistic z will be approximately the
standard normal distribution. Given the sample data below, test the claim that the proportion of male voters
who plan to vote Republican at the next presidential election is 15 percentage points more than the percentage
of female voters who plan to vote Republican. Use the P-value method of hypothesis testing and use a significance
level of 0.10.
constant c, use the test statistic:
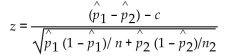 As long as
As long as  are both large, the sampling distribution of the test statistic z will be approximately the
are both large, the sampling distribution of the test statistic z will be approximately thestandard normal distribution. Given the sample data below, test the claim that the proportion of male voters
who plan to vote Republican at the next presidential election is 15 percentage points more than the percentage
of female voters who plan to vote Republican. Use the P-value method of hypothesis testing and use a significance
level of 0.10.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
45
Test the given claim about the means of two populations. Assume that two dependent samples have been
randomly selected from normally distributed populations. A test of abstract reasoning is given to a random
sample of students before and after they completed a formal logic course. The results are given below. At the
0.05 significance level, test the claim that the mean score is not affected by the course. Include your null and
alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null hypothesis, and
conclusion about the claim in your answer.
randomly selected from normally distributed populations. A test of abstract reasoning is given to a random
sample of students before and after they completed a formal logic course. The results are given below. At the
0.05 significance level, test the claim that the mean score is not affected by the course. Include your null and
alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null hypothesis, and
conclusion about the claim in your answer.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
46
Test the indicated claim about the variances or standard deviations of two populations. Assume that both
samples are independent simple random samples from populations having normal distributions. A random
sample of 16 women resulted in blood pressure levels with a standard deviation of 23 mm Hg. A random
sample of 17 men resulted in blood pressure levels with a standard deviation of 19.2 mm Hg. Use a 0.05
significance level to test the claim that blood pressure levels for women vary more than blood pressure levels
for men. Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion
about the null hypothesis, and conclusion about the claim in your answer.
samples are independent simple random samples from populations having normal distributions. A random
sample of 16 women resulted in blood pressure levels with a standard deviation of 23 mm Hg. A random
sample of 17 men resulted in blood pressure levels with a standard deviation of 19.2 mm Hg. Use a 0.05
significance level to test the claim that blood pressure levels for women vary more than blood pressure levels
for men. Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion
about the null hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
47
When testing for a difference between the means of a treatment group and a placebo group, the computer
display below is obtained. Using a 0.05 significance level, is there sufficient evidence to support the claim that
the treatment group (variable 1) comes from a population with a mean that is less than the mean for the placebo
population? Explain.
display below is obtained. Using a 0.05 significance level, is there sufficient evidence to support the claim that
the treatment group (variable 1) comes from a population with a mean that is less than the mean for the placebo
population? Explain.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
48
In a random sample of 300 women, 45% favored stricter DUI legislation. In a random sample of 200 men, 25%
favored stricter DUI legislation. Construct a 95% confidence interval for the difference between the population
proportions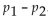 . Assume that the samples are independent and that they have been randomly selected.
. Assume that the samples are independent and that they have been randomly selected.
favored stricter DUI legislation. Construct a 95% confidence interval for the difference between the population
proportions
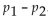 . Assume that the samples are independent and that they have been randomly selected.
. Assume that the samples are independent and that they have been randomly selected.
Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
49
Test the indicated claim about the variances or standard deviations of two populations. Assume that both
samples are independent simple random samples from populations having normal distributions. When 25
randomly selected customers enter any one of several waiting lines, their waiting times have a standard
deviation of 5.35 minutes. When 16 randomly selected customers enter a single main waiting line, their waiting
times have a standard deviation of 2.2 minutes. Use a 0.05 significance level to test the claim that there is more
variation in the waiting times when several lines are used. Include your null and alternative hypotheses, the test
statistic, P-value or critical value(s), conclusion about the null hypothesis, and conclusion about the claim in
your answer.
samples are independent simple random samples from populations having normal distributions. When 25
randomly selected customers enter any one of several waiting lines, their waiting times have a standard
deviation of 5.35 minutes. When 16 randomly selected customers enter a single main waiting line, their waiting
times have a standard deviation of 2.2 minutes. Use a 0.05 significance level to test the claim that there is more
variation in the waiting times when several lines are used. Include your null and alternative hypotheses, the test
statistic, P-value or critical value(s), conclusion about the null hypothesis, and conclusion about the claim in
your answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
50
A researcher wishes to compare how students at two different schools perform on a math test. He randomly
selects 40 students from each school and obtains their test scores. He pairs the first score from school A with the
first school from school B, the second score from school A with the second school from school B and so on. He
then performs a hypothesis test for matched pairs. Is this approach valid? Why or why not? If it is not valid,
how should the researcher have proceeded?
selects 40 students from each school and obtains their test scores. He pairs the first score from school A with the
first school from school B, the second score from school A with the second school from school B and so on. He
then performs a hypothesis test for matched pairs. Is this approach valid? Why or why not? If it is not valid,
how should the researcher have proceeded?

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
51
Assume that the two samples are independent simple random samples selected from normally distributed
populations. Do not assume that the population standard deviations are equal. A researcher wishes to
determine whether people can reduce their resting heart rate by following a particular diet. Construct a 95%
confidence interval estimate for the following data. Does the confidence interval support that the mean resting
heart rate for those on the diet is lower than that of those not on the diet? Explain your reasoning.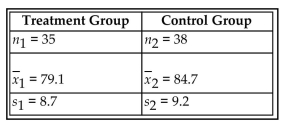
populations. Do not assume that the population standard deviations are equal. A researcher wishes to
determine whether people can reduce their resting heart rate by following a particular diet. Construct a 95%
confidence interval estimate for the following data. Does the confidence interval support that the mean resting
heart rate for those on the diet is lower than that of those not on the diet? Explain your reasoning.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
52
A Dean of Students conducted a survey to test the claim that women spend more time visiting the STEM lab
than men do. A survey was administered to a simple random sample of 15 female student volunteers and 12
male volunteers that asked, "How many minutes have you spent in the STEM lab this semester?" The results are
shown below.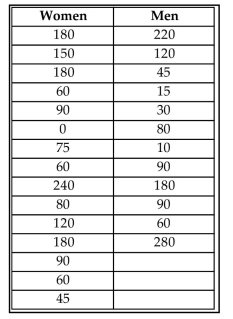 Test the claim at the 1% level of significance. Assume that the number of minutes that women and men spent in
Test the claim at the 1% level of significance. Assume that the number of minutes that women and men spent in
the STEM lab is normally distributed. Do not assume that the population standard deviations are equal. Include
your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
hypothesis, and conclusion about the claim in your answer.
than men do. A survey was administered to a simple random sample of 15 female student volunteers and 12
male volunteers that asked, "How many minutes have you spent in the STEM lab this semester?" The results are
shown below.
 Test the claim at the 1% level of significance. Assume that the number of minutes that women and men spent in
Test the claim at the 1% level of significance. Assume that the number of minutes that women and men spent inthe STEM lab is normally distributed. Do not assume that the population standard deviations are equal. Include
your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
53
Assume that the samples are independent and that they have been randomly selected. A marketing survey
involves product recognition in New York and California. Of 558 New Yorkers surveyed, 193 knew the product
while 196 out of 614 Californians knew the product. At the 0.05 significance level, test the claim that the
recognition rates are the same in both states. Include your null and alternative hypotheses, the test statistic,
P-value or critical value(s), conclusion about the null hypothesis, and conclusion about the claim in your
answer.
involves product recognition in New York and California. Of 558 New Yorkers surveyed, 193 knew the product
while 196 out of 614 Californians knew the product. At the 0.05 significance level, test the claim that the
recognition rates are the same in both states. Include your null and alternative hypotheses, the test statistic,
P-value or critical value(s), conclusion about the null hypothesis, and conclusion about the claim in your
answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
54
A random sample of 10 employees of an engineering company was selected. Each employee was asked to
report the number of sick days he/she claimed on Wednesdays and Fridays of the previous calendar year. Use
this information to test the employer's claim that more employees call in sick on Fridays than on Wednesdays.
Use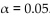 5. Assume that the differences between Wednesday's and Friday's sick day counts is normally
5. Assume that the differences between Wednesday's and Friday's sick day counts is normally
distributed.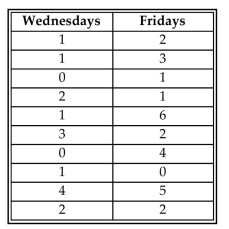 Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
hypothesis, and conclusion about the claim in your answer.
report the number of sick days he/she claimed on Wednesdays and Fridays of the previous calendar year. Use
this information to test the employer's claim that more employees call in sick on Fridays than on Wednesdays.
Use
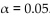 5. Assume that the differences between Wednesday's and Friday's sick day counts is normally
5. Assume that the differences between Wednesday's and Friday's sick day counts is normallydistributed.
 Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the nullhypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
55
Brian wants to obtain a confidence interval estimate of 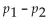 where p1 represents the proportion of American
where p1 represents the proportion of American
women who smoke and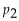 represents the proportion of American men who smoke. He randomly selects 100
represents the proportion of American men who smoke. He randomly selects 100
married couples. Among the 100 women in the sample are 21 smokers. Among the 100 men are 29 smokers. Are
the requirements for obtaining a confidence interval estimate of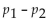 satisfied? If not, which requirement is
satisfied? If not, which requirement is
not satisfied?
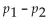 where p1 represents the proportion of American
where p1 represents the proportion of Americanwomen who smoke and
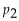 represents the proportion of American men who smoke. He randomly selects 100
represents the proportion of American men who smoke. He randomly selects 100married couples. Among the 100 women in the sample are 21 smokers. Among the 100 men are 29 smokers. Are
the requirements for obtaining a confidence interval estimate of
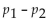 satisfied? If not, which requirement is
satisfied? If not, which requirement isnot satisfied?

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
56
Test the given claim about the means of two populations. Assume that two dependent samples have been
randomly selected from normally distributed populations. A coach uses a new technique to train gymnasts. 7
gymnasts were randomly selected and their competition scores were recorded before and after the training. The
results are shown below.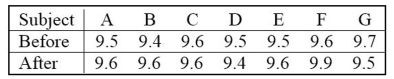 Using a 0.01 level of significance, test the claim that the training technique is effective in raising the gymnasts' scores.
Using a 0.01 level of significance, test the claim that the training technique is effective in raising the gymnasts' scores.
Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
hypothesis, and conclusion about the claim in your answer.
randomly selected from normally distributed populations. A coach uses a new technique to train gymnasts. 7
gymnasts were randomly selected and their competition scores were recorded before and after the training. The
results are shown below.
 Using a 0.01 level of significance, test the claim that the training technique is effective in raising the gymnasts' scores.
Using a 0.01 level of significance, test the claim that the training technique is effective in raising the gymnasts' scores.Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
57
Test the indicated claim about the means of two populations. Assume that the two samples are independent
simple random samples selected from normally distributed populations. Do not assume that the population
standard deviations are equal. A researcher wishes to determine whether people with high blood pressure can
reduce their blood pressure, measured in mm Hg, by following a particular diet. Use a significance level of 0.01
to test the claim that the treatment group is from a population with a smaller mean than the control group.
Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the
null hypothesis, and conclusion about the claim in your answer.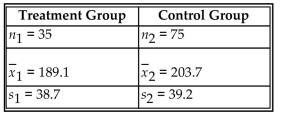
simple random samples selected from normally distributed populations. Do not assume that the population
standard deviations are equal. A researcher wishes to determine whether people with high blood pressure can
reduce their blood pressure, measured in mm Hg, by following a particular diet. Use a significance level of 0.01
to test the claim that the treatment group is from a population with a smaller mean than the control group.
Include your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the
null hypothesis, and conclusion about the claim in your answer.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
58
Identify the test statistic that should be used for testing the following given claims.
a. The mean of the differences between IQ scores of brothers and IQ scores of their sisters is equal to 0.
b. The proportion of offices with windows is equal to the proportion of offices without windows.
c. The variation among temperature inside buildings in winter is equal to the variation in the temperature inside
building in summer.
d. The mean age of female math professors is equal to the mean age of male math professors.
a. The mean of the differences between IQ scores of brothers and IQ scores of their sisters is equal to 0.
b. The proportion of offices with windows is equal to the proportion of offices without windows.
c. The variation among temperature inside buildings in winter is equal to the variation in the temperature inside
building in summer.
d. The mean age of female math professors is equal to the mean age of male math professors.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
59
Test the indicated claim about the means of two populations. Assume that the two samples are independent
simple random samples selected from normally distributed populations. Do not assume that the population
standard deviations are equal.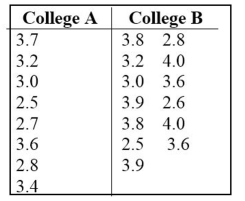 Use a 0.10 significance level to test the claim that the mean GPA of students at college A is different from the mean GPA
Use a 0.10 significance level to test the claim that the mean GPA of students at college A is different from the mean GPA
of students at college B.
simple random samples selected from normally distributed populations. Do not assume that the population
standard deviations are equal.
 Use a 0.10 significance level to test the claim that the mean GPA of students at college A is different from the mean GPA
Use a 0.10 significance level to test the claim that the mean GPA of students at college A is different from the mean GPAof students at college B.


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
60
A researcher wishes to determine whether the blood pressure of vegetarians is, on average, lower than the
blood pressure of nonvegetarians. Independent simple random samples of 85 vegetarians and 75
nonvegetarians yielded the following sample statistics for systolic blood pressure: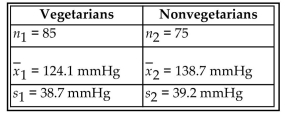 Use a significance level of 0.01 to test the claim that the mean systolic blood pressure of vegetarians is lower than the
Use a significance level of 0.01 to test the claim that the mean systolic blood pressure of vegetarians is lower than the
mean systolic blood pressure of nonvegetarians. Include your null and alternative hypotheses, the test statistic, P-value
or critical value(s), conclusion about the null hypothesis, and conclusion about the claim in your answer.
blood pressure of nonvegetarians. Independent simple random samples of 85 vegetarians and 75
nonvegetarians yielded the following sample statistics for systolic blood pressure:
 Use a significance level of 0.01 to test the claim that the mean systolic blood pressure of vegetarians is lower than the
Use a significance level of 0.01 to test the claim that the mean systolic blood pressure of vegetarians is lower than themean systolic blood pressure of nonvegetarians. Include your null and alternative hypotheses, the test statistic, P-value
or critical value(s), conclusion about the null hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
The table shows the number satisfied in their work in a sample of working adults with a college education and in a sample of working adults without a college education. Assume that you plan to use a significance level of α
= 0)05 to test the claim that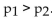 Find the critical value(s) for this hypothesis test. Do the data provide
Find the critical value(s) for this hypothesis test. Do the data provide
Sufficient evidence that a greater proportion of those with a college education are satisfied in their work?
A) z = 1.645; no
B) z = -1.645; yes
C) z = 1.96; yes
D) z = ± 1.96; no
The table shows the number satisfied in their work in a sample of working adults with a college education and in a sample of working adults without a college education. Assume that you plan to use a significance level of α
= 0)05 to test the claim that
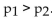 Find the critical value(s) for this hypothesis test. Do the data provide
Find the critical value(s) for this hypothesis test. Do the data provideSufficient evidence that a greater proportion of those with a college education are satisfied in their work?

A) z = 1.645; no
B) z = -1.645; yes
C) z = 1.96; yes
D) z = ± 1.96; no

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the problem.
The table shows the number of smokers in a random sample of 500 adults aged 20-24 and the number of smokers in a random sample of 450 adults aged 25-29. Assume that you plan to use a significance level of
Α = 0.10 to test the claim that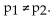 Find the critical value(s) for this hypothesis test. Do the data provide
Find the critical value(s) for this hypothesis test. Do the data provide
Sufficient evidence that the proportion of smokers in the 20-24 age group is different from the proportion of
Smokers in the 25-29 age group?
The table shows the number of smokers in a random sample of 500 adults aged 20-24 and the number of smokers in a random sample of 450 adults aged 25-29. Assume that you plan to use a significance level of
Α = 0.10 to test the claim that
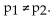 Find the critical value(s) for this hypothesis test. Do the data provide
Find the critical value(s) for this hypothesis test. Do the data provideSufficient evidence that the proportion of smokers in the 20-24 age group is different from the proportion of
Smokers in the 25-29 age group?


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
63
Assume that you plan to use a significance level of 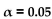 test the claim that p
test the claim that p 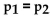 , Use the given sample sizes and
, Use the given sample sizes and
numbers of successes to find the pooled estimate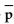 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.
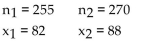
A) 0.292
B) 0.324
C) 0.227
D) 0.162
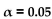 test the claim that p
test the claim that p 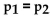 , Use the given sample sizes and
, Use the given sample sizes andnumbers of successes to find the pooled estimate
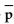 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.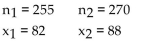
A) 0.292
B) 0.324
C) 0.227
D) 0.162

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
64
Assume that you plan to use a significance level of 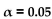 test the claim that p
test the claim that p 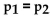 , Use the given sample sizes and
, Use the given sample sizes and
numbers of successes to find the pooled estimate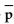 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.
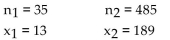
A) 0.310
B) 0.155
C) 0.388
D) 0.466
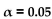 test the claim that p
test the claim that p 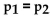 , Use the given sample sizes and
, Use the given sample sizes andnumbers of successes to find the pooled estimate
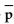 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.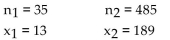
A) 0.310
B) 0.155
C) 0.388
D) 0.466

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
65
Assume that you plan to use a significance level of 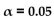 test the claim that p
test the claim that p 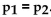 . Use the given sample sizes and
. Use the given sample sizes and
numbers of successes to find the z test statistic for the hypothesis test.

A) z = 18.096
B) z = 0.399
C) z = 0.703
D) z = 9.744
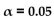 test the claim that p
test the claim that p 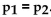 . Use the given sample sizes and
. Use the given sample sizes andnumbers of successes to find the z test statistic for the hypothesis test.

A) z = 18.096
B) z = 0.399
C) z = 0.703
D) z = 9.744

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
66
Assume that you plan to use a significance level of 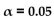 test the claim that p
test the claim that p 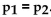 . Use the given sample sizes and
. Use the given sample sizes and
numbers of successes to find the z test statistic for the hypothesis test.
Information about movie ticket sales was printed in a movie magazine. Out of fifty PG-rated movies, 41% had ticket sales in excess of $3,000,000. Out of thirty-five R-rated movies, 17% grossed over $3,000,000.
A) z = 2.352
B) z = 7.291
C) z = 3.763
D) z = 4.704
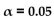 test the claim that p
test the claim that p 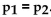 . Use the given sample sizes and
. Use the given sample sizes andnumbers of successes to find the z test statistic for the hypothesis test.
Information about movie ticket sales was printed in a movie magazine. Out of fifty PG-rated movies, 41% had ticket sales in excess of $3,000,000. Out of thirty-five R-rated movies, 17% grossed over $3,000,000.
A) z = 2.352
B) z = 7.291
C) z = 3.763
D) z = 4.704

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
67
Among 710 people selected randomly from among the eligible voters in one city, 60.6% were homeowners.
A) 431
B) 430
C) 433
D) 427
A) 431
B) 430
C) 433
D) 427

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
68
Among 780 people selected randomly from among the residents of one city, 20.38% were found to be living below the official poverty line.
A) 158
B) 164
C) 159
D) 160
A) 158
B) 164
C) 159
D) 160

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
69
Assume that you plan to use a significance level of 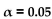 test the claim that p
test the claim that p 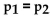 , Use the given sample sizes and
, Use the given sample sizes and
numbers of successes to find the pooled estimate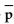 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.
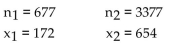
A) 0.408
B) 0.452
C) 0.204
D) 0.163
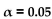 test the claim that p
test the claim that p 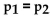 , Use the given sample sizes and
, Use the given sample sizes andnumbers of successes to find the pooled estimate
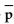 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.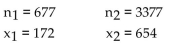
A) 0.408
B) 0.452
C) 0.204
D) 0.163

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
70
Assume that you plan to use a significance level of 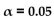 test the claim that p
test the claim that p 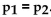 . Use the given sample sizes and
. Use the given sample sizes and
numbers of successes to find the z test statistic for the hypothesis test.
In a vote on the Clean Water bill, 46% of the 205 Democrats voted for the bill while 48% of the 230 Republicans voted for it.
A) z = -0.417
B) z = -0.250
C) z = -0.459
D) z = -0.354
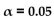 test the claim that p
test the claim that p 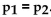 . Use the given sample sizes and
. Use the given sample sizes andnumbers of successes to find the z test statistic for the hypothesis test.
In a vote on the Clean Water bill, 46% of the 205 Democrats voted for the bill while 48% of the 230 Republicans voted for it.
A) z = -0.417
B) z = -0.250
C) z = -0.459
D) z = -0.354

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
71
Assume that you plan to use a significance level of 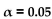 test the claim that p
test the claim that p 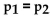 , Use the given sample sizes and
, Use the given sample sizes and
numbers of successes to find the pooled estimate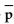 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.
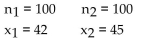
A) 0.479
B) 0.435
C) 0.305
D) 0.392
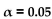 test the claim that p
test the claim that p 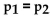 , Use the given sample sizes and
, Use the given sample sizes andnumbers of successes to find the pooled estimate
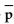 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.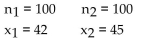
A) 0.479
B) 0.435
C) 0.305
D) 0.392

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
72
A computer manufacturer randomly selects 2680 of its computers for quality assurance and finds that 1.98% of these computers are found to be defective.
A) 58
B) 51
C) 53
D) 56
A) 58
B) 51
C) 53
D) 56

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
The table shows the number of pitchers with E.R.A's below 3.5 in a random sample of sixty pitchers from the National League and in a random sample of fifty-two pitchers from the American League. Assume that you
Plan to use a significance level of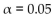 05 to test the claim that
05 to test the claim that 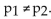 Find the critical value(s) for this
Find the critical value(s) for this
Hypothesis test. Do the data support the claim that the proportion of National League pitchers with an E.R.A.
Below 3.5 differs from the proportion of American League pitchers with an E.R.A. below 3.5?
The table shows the number of pitchers with E.R.A's below 3.5 in a random sample of sixty pitchers from the National League and in a random sample of fifty-two pitchers from the American League. Assume that you
Plan to use a significance level of
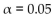 05 to test the claim that
05 to test the claim that 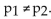 Find the critical value(s) for this
Find the critical value(s) for thisHypothesis test. Do the data support the claim that the proportion of National League pitchers with an E.R.A.
Below 3.5 differs from the proportion of American League pitchers with an E.R.A. below 3.5?


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
74
Among 690 adults selected randomly from among the residents of one town, 23.5% said that they favor stronger gun-control laws.
A) 160
B) 162
C) 163
D) 161
A) 160
B) 162
C) 163
D) 161

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
75
Assume that you plan to use a significance level of 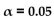 test the claim that p
test the claim that p 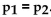 . Use the given sample sizes and
. Use the given sample sizes and
numbers of successes to find the z test statistic for the hypothesis test.
A report on the nightly news broadcast stated that 10 out of 129 households with pet dogs were burglarized and 23 out of 197 without pet dogs were burglarized.
A) z = -1.148
B) z = -0.002
C) z = -0.459
D) z = -1.952
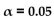 test the claim that p
test the claim that p 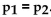 . Use the given sample sizes and
. Use the given sample sizes andnumbers of successes to find the z test statistic for the hypothesis test.
A report on the nightly news broadcast stated that 10 out of 129 households with pet dogs were burglarized and 23 out of 197 without pet dogs were burglarized.
A) z = -1.148
B) z = -0.002
C) z = -0.459
D) z = -1.952

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the problem.
The table shows the number of households burglarized in a sample of households with dogs and in a sample of households without dogs. Assume that you plan to use a significance level of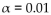 01 to test the claim that
01 to test the claim that 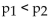 . Find the critical value(s) for this hypothesis test. Do the data support the claim that a smaller
. Find the critical value(s) for this hypothesis test. Do the data support the claim that a smaller
Proportion of households with pet dogs are burglarized?
A) z = 2.33; yes
B) z = -2.33; no
C) z = -2.575; no
D) z = -1.96; yes
The table shows the number of households burglarized in a sample of households with dogs and in a sample of households without dogs. Assume that you plan to use a significance level of
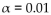 01 to test the claim that
01 to test the claim that 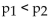 . Find the critical value(s) for this hypothesis test. Do the data support the claim that a smaller
. Find the critical value(s) for this hypothesis test. Do the data support the claim that a smallerProportion of households with pet dogs are burglarized?

A) z = 2.33; yes
B) z = -2.33; no
C) z = -2.575; no
D) z = -1.96; yes

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
77
Among 1350 randomly selected car drivers in one city, 8.74% said that they had been involved in an accident during the past year.
A) 118
B) 117
C) 119
D) 116
A) 118
B) 117
C) 119
D) 116

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
78
Assume that you plan to use a significance level of  test the claim that p
test the claim that p 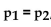 , Use the given sample sizes and
, Use the given sample sizes and
numbers of successes to find the P-value for the hypothesis test.
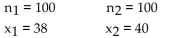
A) 0.1610
B) 0.7718
C) 0.2130
D) 0.0412
 test the claim that p
test the claim that p 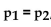 , Use the given sample sizes and
, Use the given sample sizes andnumbers of successes to find the P-value for the hypothesis test.
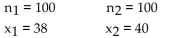
A) 0.1610
B) 0.7718
C) 0.2130
D) 0.0412

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
79
Assume that you plan to use a significance level of 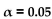 test the claim that p
test the claim that p 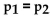 , Use the given sample sizes and
, Use the given sample sizes and
numbers of successes to find the pooled estimate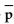 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.

A) 0.361
B) 0.260
C) 0.163
D) 0.130
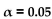 test the claim that p
test the claim that p 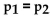 , Use the given sample sizes and
, Use the given sample sizes andnumbers of successes to find the pooled estimate
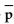 . Round your answer to the nearest thousandth.
. Round your answer to the nearest thousandth.
A) 0.361
B) 0.260
C) 0.163
D) 0.130

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
80
Assume that you plan to use a significance level of 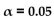 test the claim that p
test the claim that p 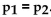 . Use the given sample sizes and
. Use the given sample sizes and
numbers of successes to find the z test statistic for the hypothesis test.
A random sampling of sixty pitchers from the National League and fifty-two pitchers from the American League showed that 19 National and 8 American League pitchers had E.R.A's below 3.5.
A) z = 272.163
B) z = 2.009
C) z = 2.612
D) z = 22.404
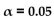 test the claim that p
test the claim that p 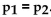 . Use the given sample sizes and
. Use the given sample sizes andnumbers of successes to find the z test statistic for the hypothesis test.
A random sampling of sixty pitchers from the National League and fifty-two pitchers from the American League showed that 19 National and 8 American League pitchers had E.R.A's below 3.5.
A) z = 272.163
B) z = 2.009
C) z = 2.612
D) z = 22.404

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck



