Deck 12: Assemble-To-Order, Make-To-Order, and Quick Response With Reactive Capacity
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/13
Play
Full screen (f)
Deck 12: Assemble-To-Order, Make-To-Order, and Quick Response With Reactive Capacity
1
(O'Neill) Consider the case in the relationship between O'Neill and TEC with unlimited, but expensive, reactive capacity, that is, TEC allows O'Neill to submit a second order but charges O'Neill a premium for those units. (See Figure 12.1.) Instead of a 20 percent premium, suppose TEC were to charge O'Neill only a 10 percent premium for units in the second order.
a. What is O'Neill's optimal first order quantity of Hammer 3/2s?
b. What is O'Neill's maximum expected profit with the Hammer 3/2?
c. How many units should TEC expect O'Neill will order in the second order?
d. What fraction of the mismatch cost is eliminated by this reactive capacity opportunity?
a. What is O'Neill's optimal first order quantity of Hammer 3/2s?
b. What is O'Neill's maximum expected profit with the Hammer 3/2?
c. How many units should TEC expect O'Neill will order in the second order?
d. What fraction of the mismatch cost is eliminated by this reactive capacity opportunity?
In a single-period inventory model, the order size decision is made by a marginal analysis. In this analysis, the optimal order quantity occurs when the probability of demand, D being less than or equal to the order quantity, Q equals the critical ratio. In other words,
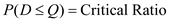 ( CR ) where CR can be computed as:
( CR ) where CR can be computed as:
 Where
Where
 and
and
 are the cost per unit of demand underestimated and that of demand overestimated respectively.Note the following values given in the question:
are the cost per unit of demand underestimated and that of demand overestimated respectively.Note the following values given in the question:
First order cost = $110
Salvage value = $90
Mean demand = 3,192
Standard deviation of demand = 1,181
Selling price = $180
a.Compute the optimal first order quantity as follows:
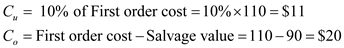 Compute the critical ratio using the following formula:
Compute the critical ratio using the following formula:
 For optimal order quantity, Q , the distribution function, F(Q) must be equal to the critical ratio. The nearest value of F ( z ) is 0.3557 and this happens for
For optimal order quantity, Q , the distribution function, F(Q) must be equal to the critical ratio. The nearest value of F ( z ) is 0.3557 and this happens for
 .Compute corresponding order quantity using the formula
.Compute corresponding order quantity using the formula
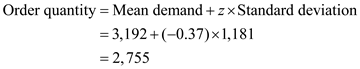 So, the optimal first order quantity is
So, the optimal first order quantity is
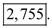 b.Compute the maximum expected profit by multiplying the gross profit by the expected demand.Compute the gross profit as:
b.Compute the maximum expected profit by multiplying the gross profit by the expected demand.Compute the gross profit as:
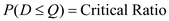 0
0
So,
 1
1
So, the maximum expected profit is
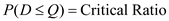 2
2
c.The number of units will be ordered for the second time only when an equal number of units will fall short of demand. In other words, compute the expected lost sales given the optimal first order quantity.The standard normal variable, z was found to be
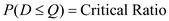 3
3
The corresponding loss function,
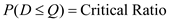 4
4
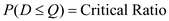 5
5
Rounding off to the nearest integer, the expected lost sales or the number of units ordered for the second time is
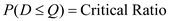 6
6
d.The mismatch cost is the sum of the cost incurred due to lost sales and the cost of the left-over inventory.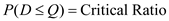 7
7
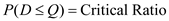 8
8
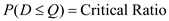 9
9
Without the opportunity of second order, the mismatch cost was $31,680 (Refer to the solved problem of the chapter in section 12.4).So,
 0
0
So, the reduction is the mismatch cost will be
 1
1
.
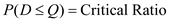 ( CR ) where CR can be computed as:
( CR ) where CR can be computed as: Where
Where  and
and  are the cost per unit of demand underestimated and that of demand overestimated respectively.Note the following values given in the question:
are the cost per unit of demand underestimated and that of demand overestimated respectively.Note the following values given in the question:First order cost = $110
Salvage value = $90
Mean demand = 3,192
Standard deviation of demand = 1,181
Selling price = $180
a.Compute the optimal first order quantity as follows:
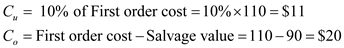 Compute the critical ratio using the following formula:
Compute the critical ratio using the following formula: For optimal order quantity, Q , the distribution function, F(Q) must be equal to the critical ratio. The nearest value of F ( z ) is 0.3557 and this happens for
For optimal order quantity, Q , the distribution function, F(Q) must be equal to the critical ratio. The nearest value of F ( z ) is 0.3557 and this happens for  .Compute corresponding order quantity using the formula
.Compute corresponding order quantity using the formula 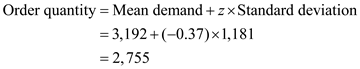 So, the optimal first order quantity is
So, the optimal first order quantity is 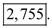 b.Compute the maximum expected profit by multiplying the gross profit by the expected demand.Compute the gross profit as:
b.Compute the maximum expected profit by multiplying the gross profit by the expected demand.Compute the gross profit as: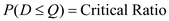 0
0So,
 1
1So, the maximum expected profit is
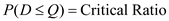 2
2c.The number of units will be ordered for the second time only when an equal number of units will fall short of demand. In other words, compute the expected lost sales given the optimal first order quantity.The standard normal variable, z was found to be
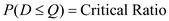 3
3The corresponding loss function,
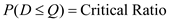 4
4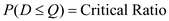 5
5Rounding off to the nearest integer, the expected lost sales or the number of units ordered for the second time is
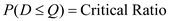 6
6d.The mismatch cost is the sum of the cost incurred due to lost sales and the cost of the left-over inventory.
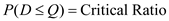 7
7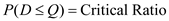 8
8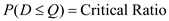 9
9Without the opportunity of second order, the mismatch cost was $31,680 (Refer to the solved problem of the chapter in section 12.4).So,
 0
0So, the reduction is the mismatch cost will be
 1
1.
2
(Teddy Bower) Teddy Bower sources a parka from an Asian supplier for $10 each and sells them to customers for $22 each. Leftover parkas at the end of the season have no salvage value. (Recall Q11.6.) The demand forecast is normally distributed with mean 2,100 and standard deviation 1,200. Now suppose Teddy Bower found a reliable vendor in the United States that can produce parkas very quickly but at a higher price than Teddy Bower's Asian supplier. Hence, in addition to parkas from Asia, Teddy Bower can buy an unlimited quantity of additional parkas from this American vendor at $15 each after demand is known.
a. Suppose Teddy Bower orders 1,500 parkas from the Asian supplier. What is the probability that Teddy Bower will order from the American supplier once demand is known?
b. Again assume that Teddy Bower orders 1,500 parkas from the Asian supplier. What is the American supplier's expected demand; that is, how many parkas should the American supplier expect that Teddy Bower will order?
c. Given the opportunity to order from the American supplier at $15 per parka, what order quantity from its Asian supplier now maximizes Teddy Bower's expected profit?
d. Given the order quantity evaluated in part c, what is Teddy Bower's expected profit?
e. If Teddy Bower didn't order any parkas from the Asian supplier, then what would Teddy Bower's expected profit be?
a. Suppose Teddy Bower orders 1,500 parkas from the Asian supplier. What is the probability that Teddy Bower will order from the American supplier once demand is known?
b. Again assume that Teddy Bower orders 1,500 parkas from the Asian supplier. What is the American supplier's expected demand; that is, how many parkas should the American supplier expect that Teddy Bower will order?
c. Given the opportunity to order from the American supplier at $15 per parka, what order quantity from its Asian supplier now maximizes Teddy Bower's expected profit?
d. Given the order quantity evaluated in part c, what is Teddy Bower's expected profit?
e. If Teddy Bower didn't order any parkas from the Asian supplier, then what would Teddy Bower's expected profit be?
In a single-period inventory model, the order size decision is made by a marginal analysis. In this analysis, the optimal order quantity occurs when the probability of demand, D being less than or equal to the order quantity, Q equals the critical ratio. In other words,
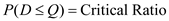 ( CR ) where CR can be computed as:
( CR ) where CR can be computed as:
 Where
Where
 and
and
 are the cost per unit of demand underestimated and that of demand overestimated respectively.Note the following information given in the question:
are the cost per unit of demand underestimated and that of demand overestimated respectively.Note the following information given in the question:
Average demand,
 Standard deviation of demand,
Standard deviation of demand,
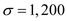 Cost in case of the American supplier = $15
Cost in case of the American supplier = $15
Cost in case of the Asian supplier = $10
Salvage value = $0
Selling price = $22
a.Note that when the demand is greater than the order quantity from the Asian supplier, then only orders will be placed from the American supplier.The order quantity from the Asian supplier, Q = 1,500
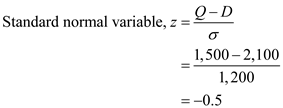 The corresponding cumulative distribution function is computed by the following Excel formula:
The corresponding cumulative distribution function is computed by the following Excel formula:
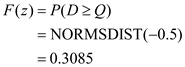
 So, the probability that any order will be placed from the American supplier is
So, the probability that any order will be placed from the American supplier is
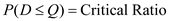 0
0
b.The American suppliers expected demand is equal to the expected lost sales considering the Asian supplier only.The order quantity from the Asian supplier, Q = 1,500
The standard normal variable, z = -0.5
Corresponding loss function, L (-0.5) = 0.698
The expected lost sales
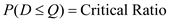 1
1
So, the expected demand from the American supplier is
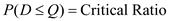 2
2
c.Compute the optimal order size for the Asian supplier as follows:
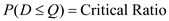 3
3
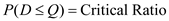 4
4
the optimal order quantity occurs when the probability of demand, D being less than or equal to the order quantity, Q equals the critical ratio. In other words,
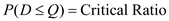 5
5
The nearest value of F ( z ), from the table, is 0.3300 and this happens for
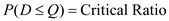 6
6
.Compute corresponding order quantity using the formula
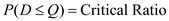 7
7
So, the optimal order size for the Asian supplier is
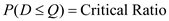 8
8
d.Compute the expected profit as follows:
Given the order size from the Asian supplier, Q = 1,583
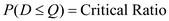 9
9
The loss function corresponding to this value,
 0
0
Expected lost sales (or order to the American supplier)
 1
1
So,
 2
2
 3
3
 4
4
So, the expected profit is
 5
5
e.In this case, the entire demand will be fulfilled by the American supplier.Compute the gross profit margin as:
 6
6
 7
7
So, the expected profit will be
 8
8
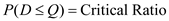 ( CR ) where CR can be computed as:
( CR ) where CR can be computed as: Where
Where  and
and  are the cost per unit of demand underestimated and that of demand overestimated respectively.Note the following information given in the question:
are the cost per unit of demand underestimated and that of demand overestimated respectively.Note the following information given in the question:Average demand,
 Standard deviation of demand,
Standard deviation of demand, 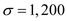 Cost in case of the American supplier = $15
Cost in case of the American supplier = $15Cost in case of the Asian supplier = $10
Salvage value = $0
Selling price = $22
a.Note that when the demand is greater than the order quantity from the Asian supplier, then only orders will be placed from the American supplier.The order quantity from the Asian supplier, Q = 1,500
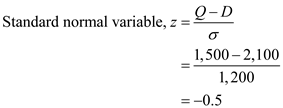 The corresponding cumulative distribution function is computed by the following Excel formula:
The corresponding cumulative distribution function is computed by the following Excel formula: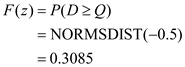
 So, the probability that any order will be placed from the American supplier is
So, the probability that any order will be placed from the American supplier is 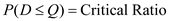 0
0b.The American suppliers expected demand is equal to the expected lost sales considering the Asian supplier only.The order quantity from the Asian supplier, Q = 1,500
The standard normal variable, z = -0.5
Corresponding loss function, L (-0.5) = 0.698
The expected lost sales
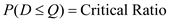 1
1So, the expected demand from the American supplier is
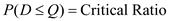 2
2c.Compute the optimal order size for the Asian supplier as follows:
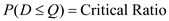 3
3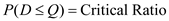 4
4the optimal order quantity occurs when the probability of demand, D being less than or equal to the order quantity, Q equals the critical ratio. In other words,
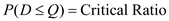 5
5The nearest value of F ( z ), from the table, is 0.3300 and this happens for
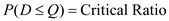 6
6.Compute corresponding order quantity using the formula
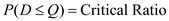 7
7So, the optimal order size for the Asian supplier is
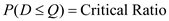 8
8d.Compute the expected profit as follows:
Given the order size from the Asian supplier, Q = 1,583
 9
9The loss function corresponding to this value,
 0
0Expected lost sales (or order to the American supplier)
 1
1So,
 2
2 3
3 4
4So, the expected profit is
 5
5e.In this case, the entire demand will be fulfilled by the American supplier.Compute the gross profit margin as:
 6
6 7
7So, the expected profit will be
 8
8 3
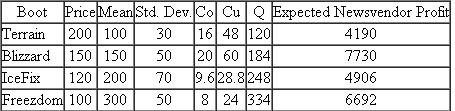
(Nordic Boots) Nordic Inc. has designed four ski boot styles it plans to sell in the next winter season: Terrain, Blizzard, IceFix, and Freezdom. Nordic can produce some ski boot styles well in advance of the selling season, with the remaining styles produced after the next Ski Elite Athletes Trade (SEAT) show that occurs before the selling season. At the time it makes its initial production decision, Nordic's forecast for each boot's demand is normally distributed with means and standard deviations listed in the table below. The table also lists results from the newsvendor model when expected profit is maximized.
 After the trade show, and before it makes its final production decision, Nordic will know exact demand for each boot.
After the trade show, and before it makes its final production decision, Nordic will know exact demand for each boot.
a. What is Nordic's expected profit if Nordic chooses to produce all four boot styles before the SEAT show?
b. What is Nordic's expected profit if Nordic chooses to produce every boot style after the SEAT show (and assuming that all of its production arrives by the start of the selling season)?
c. Because the SEAT show concludes shortly before the selling season, Nordic has limited capacity for production after the show. As a result, it needs to produce at least 300 pairs of boots before the show. Recall, each boot style is produced either before or after the show (i.e., no style is produced both before and after the show). How many pairs of boots should Nordic produce before the SEAT show?
 After the trade show, and before it makes its final production decision, Nordic will know exact demand for each boot.
After the trade show, and before it makes its final production decision, Nordic will know exact demand for each boot.a. What is Nordic's expected profit if Nordic chooses to produce all four boot styles before the SEAT show?
b. What is Nordic's expected profit if Nordic chooses to produce every boot style after the SEAT show (and assuming that all of its production arrives by the start of the selling season)?
c. Because the SEAT show concludes shortly before the selling season, Nordic has limited capacity for production after the show. As a result, it needs to produce at least 300 pairs of boots before the show. Recall, each boot style is produced either before or after the show (i.e., no style is produced both before and after the show). How many pairs of boots should Nordic produce before the SEAT show?
A supplier uses a certain lead time to deliver items to the manufacturer. It can complete the task in a lesser lead time if the reactive capacity is kept limited. Under the limited reactive capacity scheme, the idea is to realize a portion of demand before the supply has already taken place. The forecast information is strengthened by encouraging the retailers to pre-book portion of orders. The manufacturer uses two orders to buy items from the suppliers. There is always a minimum limit of the first order quantity because the lead time after the second order is placed is too short for the supplier to supply large orders. Items which have smaller mismatch cost per unit of order, are ordered by the manufacturer in the first order just covering the minimum total first order limit constraint.a.The expected total profit if all the products are ordered before the trade show will be the sum of the newsvendor profits.So,
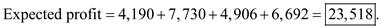 b.If a product is ordered entirely after the trade show, then the demand becomes certain to its mean value and the expected profit is the product of the mean demand and the cost of underage.So,
b.If a product is ordered entirely after the trade show, then the demand becomes certain to its mean value and the expected profit is the product of the mean demand and the cost of underage.So,
 c.Compute the mismatch cost for each item by subtracting the expected profit from the maximum profit. Divide the mismatch cost by the respective order quantity to find the mismatch cost-order quantity ratio. Based on the ascending order of this ratio, include the items to be ordered in the first order just exceeding the minimum order quantity for the first order which is 300 units.Use the following excel format to compute the mismatch cost-order quantity ratio.
c.Compute the mismatch cost for each item by subtracting the expected profit from the maximum profit. Divide the mismatch cost by the respective order quantity to find the mismatch cost-order quantity ratio. Based on the ascending order of this ratio, include the items to be ordered in the first order just exceeding the minimum order quantity for the first order which is 300 units.Use the following excel format to compute the mismatch cost-order quantity ratio.  Results
Results
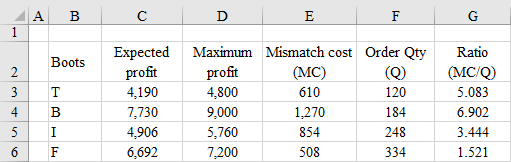 The minimum ratio occurs for item-F. Its order quantity is 334 which is just exceeding the minimum first order limit which is 300.
The minimum ratio occurs for item-F. Its order quantity is 334 which is just exceeding the minimum first order limit which is 300.
So, the company should produce only item-F with production quantity
 before the trade show.
before the trade show.
 b.If a product is ordered entirely after the trade show, then the demand becomes certain to its mean value and the expected profit is the product of the mean demand and the cost of underage.So,
b.If a product is ordered entirely after the trade show, then the demand becomes certain to its mean value and the expected profit is the product of the mean demand and the cost of underage.So, c.Compute the mismatch cost for each item by subtracting the expected profit from the maximum profit. Divide the mismatch cost by the respective order quantity to find the mismatch cost-order quantity ratio. Based on the ascending order of this ratio, include the items to be ordered in the first order just exceeding the minimum order quantity for the first order which is 300 units.Use the following excel format to compute the mismatch cost-order quantity ratio.
c.Compute the mismatch cost for each item by subtracting the expected profit from the maximum profit. Divide the mismatch cost by the respective order quantity to find the mismatch cost-order quantity ratio. Based on the ascending order of this ratio, include the items to be ordered in the first order just exceeding the minimum order quantity for the first order which is 300 units.Use the following excel format to compute the mismatch cost-order quantity ratio.  Results
Results The minimum ratio occurs for item-F. Its order quantity is 334 which is just exceeding the minimum first order limit which is 300.
The minimum ratio occurs for item-F. Its order quantity is 334 which is just exceeding the minimum first order limit which is 300. So, the company should produce only item-F with production quantity
 before the trade show.
before the trade show. 4
(Flextrola) Flextrola, Inc., an electronics system integrator, is developing a new product. As mentioned in Q11.4, Solectrics can produce a key component for this product. Solectrics sells this component to Flextrola for $72 per unit and Flextrola must submit its order well in advance of the selling season. Flextrola's demand forecast is a normal distribution with mean of 1,000 and standard deviation of 600. Flextrola sells each unit, after integrating some software, for $121. Leftover units at the end of the season are sold for $50. Xandova Electronics (XE for short) approached Flextrola with the possibility of also supplying Flextrola with this component. XE's main value proposition is that they offer 100 percent fill rate and one-day delivery on all of Flextrola's orders, no matter when the orders are submitted. Flextrola promises its customers a one-week lead time, so the one- day lead time from XE would allow Flextrola to operate with make-to-order production. (The software integration that Flextrola performs can be done within one day.) XE's price is $83.50 per unit.
a. Suppose Flextrola were to procure exclusively from XE. What would be Flextrola's expected profit?
b. Suppose Flextrola plans to procure from both Solectrics and XE; that is, Flextrola will order some amount from Solectrics before the season and then use XE during the selling season to fill demands that exceed that order quantity. How many units should Flextrola order from Solectrics to maximize expected profit?
c. Concerned about the potential loss of business, Solectrics is willing to renegotiate their offer. Solectrics now offers Flextrola an "options contract": Before the season starts, Flextrola purchases Q options and pays Solectrics $25 per option. During the selling season, Flextrola can exercise up to the Q purchased options with a one-day lead time-that is, Solectrics delivers on each exercised option within one day-and the exercise price is $50 per unit. If Flextrola wishes additional units beyond the options purchased, Solectrics will deliver units at XE's price, $83.50. For example, suppose Flextrola purchases 1,500 options but then needs 1,600 units. Flextrola exercises the 1,500 options at $50 each and then orders an additional 100 units at $83.50 each. How many options should Flextrola purchase from Solectrics?
d. Continuing with part c, given the number of options purchased, what is Flextrola's expected profit?
a. Suppose Flextrola were to procure exclusively from XE. What would be Flextrola's expected profit?
b. Suppose Flextrola plans to procure from both Solectrics and XE; that is, Flextrola will order some amount from Solectrics before the season and then use XE during the selling season to fill demands that exceed that order quantity. How many units should Flextrola order from Solectrics to maximize expected profit?
c. Concerned about the potential loss of business, Solectrics is willing to renegotiate their offer. Solectrics now offers Flextrola an "options contract": Before the season starts, Flextrola purchases Q options and pays Solectrics $25 per option. During the selling season, Flextrola can exercise up to the Q purchased options with a one-day lead time-that is, Solectrics delivers on each exercised option within one day-and the exercise price is $50 per unit. If Flextrola wishes additional units beyond the options purchased, Solectrics will deliver units at XE's price, $83.50. For example, suppose Flextrola purchases 1,500 options but then needs 1,600 units. Flextrola exercises the 1,500 options at $50 each and then orders an additional 100 units at $83.50 each. How many options should Flextrola purchase from Solectrics?
d. Continuing with part c, given the number of options purchased, what is Flextrola's expected profit?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
5
(Three Kings) Recall Q11.9. Erica Zhang must decide how many Three Kings baking dishes to purchase for her upcoming promotion. Forecasted demand is normally distributed with mean 980 and standard deviation 354. Leftover cake dishes are sold to a discounter for $15. But now the department store just instituted a new policy regarding stockouts. If a promotion item is out of stock, then a customer can request a comparable item for the same price as the stocked-out item. For example, if the store runs out of Three Kings baking dishes, then a customer can request instead a regular baking dish and pay the Three Kings price. The department store has plenty of regular baking dishes, so there is no risk of running out of them. Furthermore, Erica believes that all of her Three Kings customers would be willing to switch to the regular baking dish should they experience a stockout. Data on the Three Kings baking dish as well as the regular baking dish follow.
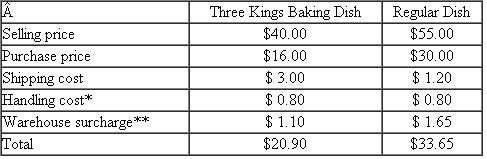 * Estimate of variable cost to uncrate, clean, and transport a dish to the housewares department.
* Estimate of variable cost to uncrate, clean, and transport a dish to the housewares department.
** Allocation of fixed overhead expenses in the shipping and receiving department.
a. How many Three Kings baking dishes should she purchase?
b. Is the department store better off with this new substitution policy?
c. Suppose Erica now believes that only half of her Three Kings customers would be willing to substitute the regular baking dish. Given this new belief, how many Three Kings baking dishes should she purchase?
 * Estimate of variable cost to uncrate, clean, and transport a dish to the housewares department.
* Estimate of variable cost to uncrate, clean, and transport a dish to the housewares department.** Allocation of fixed overhead expenses in the shipping and receiving department.
a. How many Three Kings baking dishes should she purchase?
b. Is the department store better off with this new substitution policy?
c. Suppose Erica now believes that only half of her Three Kings customers would be willing to substitute the regular baking dish. Given this new belief, how many Three Kings baking dishes should she purchase?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
6
(Wildcat Cellular) Marisol is new to town and is in the market for cellular phone service. She has settled on Wildcat Cellular, which will give her a free phone if she signs a one-year contract. Wildcat offers several calling plans. One plan that she is considering is called "Pick Your Minutes." Under this plan, she would specify a quantity of minutes, say x, per month that she would buy at 5? per minute. Thus, her upfront cost would be $0.05 x. If her usage is less than this quantity x in a given month, she loses the minutes. If her usage in a month exceeds this quantity x , she would have to pay 40? for each extra minute (that is, each minute used beyond x ). For example, if she contracts for x = 120 minutes per month and her actual usage is 40 minutes, her total bill is $120 × 0.05 = $6.00. However, if actual usage is 130 minutes, her total bill would be $120 × 0.05 + (130 - 120) × 0.40 = $10.00. The same rates apply whether the call is local or long distance. Once she signs the contract, she cannot change the number of minutes specified for a year. Marisol estimates that her monthly needs are best approximated by the normal distribution, with a mean of 250 minutes and a standard deviation of 24 minutes.
a. If Marisol chooses the "Pick Your Minutes" plan described above, how many minutes should she contract for?
b. Instead, Marisol chooses to contract for 240 minutes. Under this contract, how much (in dollars) would she expect to pay at 40 cents per minute?
c. A friend advises Marisol to contract for 280 minutes to ensure limited surcharge payments (i.e., the 40-cents-per-minute payments). Under this contract, how many minutes would she expect to waste (i.e., unused minutes per month)?
d. If Marisol contracts for 260 minutes, what would be her approximate expected monthly cell phone bill?
e. Marisol has decided that she indeed does not like surcharge fees (the 40-cents-per-minute fee for her usage in excess of her monthly contracted minutes). How many minutes should she contract for if she wants only a 5 percent chance of incurring any surcharge fee?
f. Wildcat Cellular offers another plan called "No Minimum" that also has a $5.00 fixed fee per month but requires no commitment in terms of the number of minutes per month. Instead, the user is billed 7? per minute for her actual usage. Thus, if her actual usage is 40 minutes in a month, her bill would be $5.00 + 40 × 0.07 = $7.80. Marisol is trying to decide between the "Pick Your Minutes" plan described above and the "No Minimum" plan. Which should she choose?
a. If Marisol chooses the "Pick Your Minutes" plan described above, how many minutes should she contract for?
b. Instead, Marisol chooses to contract for 240 minutes. Under this contract, how much (in dollars) would she expect to pay at 40 cents per minute?
c. A friend advises Marisol to contract for 280 minutes to ensure limited surcharge payments (i.e., the 40-cents-per-minute payments). Under this contract, how many minutes would she expect to waste (i.e., unused minutes per month)?
d. If Marisol contracts for 260 minutes, what would be her approximate expected monthly cell phone bill?
e. Marisol has decided that she indeed does not like surcharge fees (the 40-cents-per-minute fee for her usage in excess of her monthly contracted minutes). How many minutes should she contract for if she wants only a 5 percent chance of incurring any surcharge fee?
f. Wildcat Cellular offers another plan called "No Minimum" that also has a $5.00 fixed fee per month but requires no commitment in terms of the number of minutes per month. Instead, the user is billed 7? per minute for her actual usage. Thus, if her actual usage is 40 minutes in a month, her bill would be $5.00 + 40 × 0.07 = $7.80. Marisol is trying to decide between the "Pick Your Minutes" plan described above and the "No Minimum" plan. Which should she choose?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
7
(Sarah's Wedding) Sarah is planning her wedding. She and her fiancé have signed a contract with a caterer that calls for them to tell the caterer the number of guests that will attend the reception a week before the actual event. This "final number" will determine how much they have to pay the caterer; they must pay $60 per guest that they commit to. If, for example, they tell the caterer that they expect 90 guests, they must pay $5,400 (= 90 × $60) even if only, say, 84 guests show up. The contract calls for a higher rate of $85 per extra guest for the number of guests beyond what the couple commits to. Thus, if Sarah and her fiancé commit to 90 guests but 92 show up, they must pay $5,570 (the original $5,400 plus 2 × $85).
The problem Sarah faces is that she still does not know the exact number of guests to expect. Despite asking that friends and family members reply to their invitations a month ago, some uncertainty remains: her brother may-or may not-bring his new girlfriend; her fiancé's college roommate may-or may not-be able to take a vacation from work; and so forth. Sarah has determined that the expected number of guests (i.e., the mean number) is 100, but the actual number could be anywhere from 84 to 116:
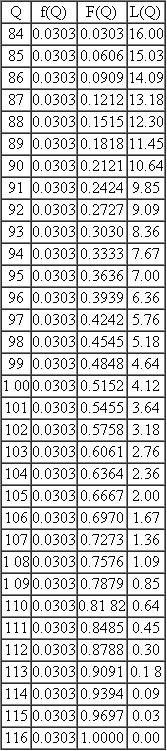 Q = Number of guests that show up to the wedding
Q = Number of guests that show up to the wedding
f ( Q ) = Density function = Prob{ Q guests show up}
F ( Q ) = Distribution function = Prob{ Q or fewer guests show up}
L ( Q ) = Loss function = Expected number of guests above Q
a. How many guests should Sarah commit to with the caterer
b. Suppose Sarah commits to 105 guests. What is Sarah's expected bill?
c. Suppose that the caterer is willing to alter the contract so that if fewer than the number of guests they commit to show up, they will get a partial refund. In particular, they only have to pay $45 for each "no-show." For example, if they commit to 90 but only 84 show, they will have to pay 84 × $60 + 6 × $45 = $5,310. Now how many guests should she commit to?
d. The caterer offers Sarah another option. She could pay $70 per guest, no matter how many guests show up; that is, she wouldn't have to commit to any number before the wedding. Should Sarah prefer this option or the original option ($60 per committed guest and $85 each guest beyond the commitment)?
The problem Sarah faces is that she still does not know the exact number of guests to expect. Despite asking that friends and family members reply to their invitations a month ago, some uncertainty remains: her brother may-or may not-bring his new girlfriend; her fiancé's college roommate may-or may not-be able to take a vacation from work; and so forth. Sarah has determined that the expected number of guests (i.e., the mean number) is 100, but the actual number could be anywhere from 84 to 116:
 Q = Number of guests that show up to the wedding
Q = Number of guests that show up to the weddingf ( Q ) = Density function = Prob{ Q guests show up}
F ( Q ) = Distribution function = Prob{ Q or fewer guests show up}
L ( Q ) = Loss function = Expected number of guests above Q
a. How many guests should Sarah commit to with the caterer
b. Suppose Sarah commits to 105 guests. What is Sarah's expected bill?
c. Suppose that the caterer is willing to alter the contract so that if fewer than the number of guests they commit to show up, they will get a partial refund. In particular, they only have to pay $45 for each "no-show." For example, if they commit to 90 but only 84 show, they will have to pay 84 × $60 + 6 × $45 = $5,310. Now how many guests should she commit to?
d. The caterer offers Sarah another option. She could pay $70 per guest, no matter how many guests show up; that is, she wouldn't have to commit to any number before the wedding. Should Sarah prefer this option or the original option ($60 per committed guest and $85 each guest beyond the commitment)?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
8
(Lucky Smokes) Lucky Smokes currently operates a warehouse that serves the Virginia market. Some trucks arrive at the warehouse filled with goods to be stored in the warehouse. Other trucks arrive at the warehouse empty to be loaded with goods. Based on the number of trucks that arrive at the warehouse in a week, the firm is able to accurately estimate the total number of labor hours that are required to finish all of the loading and unloading. The following histogram plots these estimates for each week over the past two
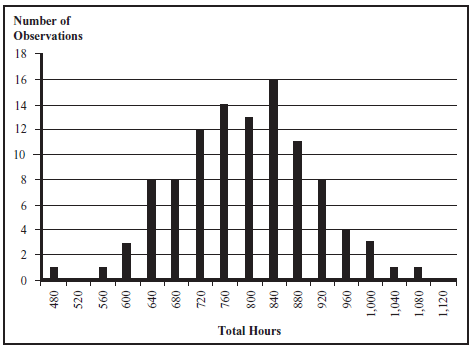
years. (There are a total of 104 weeks recorded in the graph.) For example, there were three weeks in this period that required 600 total labor hours and only one week that recorded 1,080 hours of required labor.
The mean of the data is 793 and the standard deviation is 111. Labor is the primary variable cost in the operation of a warehouse. The Virginia warehouse employed 20 workers, who were guaranteed at least 40 hours of pay per week. Thus, in weeks with less than 800 hours of required labor, the workers either went home early on some days or were idle. On weeks with more than 800 hours of required labor, the extra hours were obtained with overtime. Workers were paid time and a half for each hour of overtime.
You have been placed in charge of a new warehouse scheduled to serve the North Carolina market. Marketing suggests that the volume for this warehouse should be comparable to the Virginia warehouse. Assume that you must pay each worker for at least 40 hours of work per week and time and a half for each hour of overtime. Assume there is no limit on overtime for a given week. Further, assume you approximate your workload requirement with a normal distribution.
a. If you hire 22 workers, how many weeks a year should you expect to use overtime?
b. If you hire 18 workers, how many weeks a year will your workers be underutilized?
c. If you are interested in minimizing your labor cost, how many workers should you hire (again, assuming your workload forecast is normally distributed)?
d. You are now concerned the normal distribution might not be appropriate. For example, you can't hire 20.5 workers. What is the optimal number of workers to hire if you use the empirical distribution function constructed with the data in the above histogram?

years. (There are a total of 104 weeks recorded in the graph.) For example, there were three weeks in this period that required 600 total labor hours and only one week that recorded 1,080 hours of required labor.
The mean of the data is 793 and the standard deviation is 111. Labor is the primary variable cost in the operation of a warehouse. The Virginia warehouse employed 20 workers, who were guaranteed at least 40 hours of pay per week. Thus, in weeks with less than 800 hours of required labor, the workers either went home early on some days or were idle. On weeks with more than 800 hours of required labor, the extra hours were obtained with overtime. Workers were paid time and a half for each hour of overtime.
You have been placed in charge of a new warehouse scheduled to serve the North Carolina market. Marketing suggests that the volume for this warehouse should be comparable to the Virginia warehouse. Assume that you must pay each worker for at least 40 hours of work per week and time and a half for each hour of overtime. Assume there is no limit on overtime for a given week. Further, assume you approximate your workload requirement with a normal distribution.
a. If you hire 22 workers, how many weeks a year should you expect to use overtime?
b. If you hire 18 workers, how many weeks a year will your workers be underutilized?
c. If you are interested in minimizing your labor cost, how many workers should you hire (again, assuming your workload forecast is normally distributed)?
d. You are now concerned the normal distribution might not be appropriate. For example, you can't hire 20.5 workers. What is the optimal number of workers to hire if you use the empirical distribution function constructed with the data in the above histogram?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
9
(Shillings) You are traveling abroad and have only American dollars with you. You are currently in the capital but you will soon be heading out to a small town for an extended stay. In the town, no one takes credit cards and they only accept the domestic currency (shillings). In the capital, you can convert dollars to shillings at a rate of two shillings per dollar. In the town, you learn that one dollar only buys 1.6 shillings. Upon your return to the capital at the end of your trip, you can convert shillings back to dollars at a rate of 2.5 shillings per dollar. You estimate that your expenditures in the town will be normally distributed with mean of 400 shillings and standard deviation of 100 shillings.
a. How many dollars should you convert to shillings before leaving the capital?
b. After some thought, you feel that it might be embarrassing if you run out of shillings and need to ask to convert additional dollars, so you really do not want to run out of shillings. How many dollars should you convert to shillings if you want to ensure there is no more than a 1 in 200 chance you will run out of shillings?
a. How many dollars should you convert to shillings before leaving the capital?
b. After some thought, you feel that it might be embarrassing if you run out of shillings and need to ask to convert additional dollars, so you really do not want to run out of shillings. How many dollars should you convert to shillings if you want to ensure there is no more than a 1 in 200 chance you will run out of shillings?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the relationship between TEC and O'Neill with unlimited, but expensive, reactive capacity. Recall that TEC is willing to give O'Neill a midseason replenishment (see Figure 12.1) but charges O'Neill a 20 percent premium above the regular wholesale price of $110 for those units. Suppose TEC's gross margin is 25 percent of its selling price for units produced in the first production run. However, TEC estimates that its production cost per unit for the second production run (any units produced during the season after receiving O'Neill's second order) is twice as large as units produced for the initial order. Wetsuits produced that O'Neill does not order need to be salvaged at the end of the season. With O'Neill's permission, TEC estimates it can earn $30 per suit by selling the extra suits in Asian markets.
a. What is TEC's expected profit with the traditional arrangement (i.e., a single order by O'Neill well in advance of the selling season)? Recall that O'Neill's optimal newsvendor quantity is 4,101 units.
b. What is TEC's expected profit if it offers the reactive capacity to O'Neill and TEC's first production run equals O'Neill's first production order? Assume the demand forecast is normally distributed with mean 3,192 and standard deviation 1,181. Recall, O'Neill's optimal first order is 3,263 and O'Neill's expected second order is 437 units.
c. What is TEC's optimal first production quantity if its CEO authorizes its production manager to choose a quantity that is greater than O'Neill's first order?
d. Given the order chosen in part c, what is TEC's expected profit? (Warning: this is a hard question.)
a. What is TEC's expected profit with the traditional arrangement (i.e., a single order by O'Neill well in advance of the selling season)? Recall that O'Neill's optimal newsvendor quantity is 4,101 units.
b. What is TEC's expected profit if it offers the reactive capacity to O'Neill and TEC's first production run equals O'Neill's first production order? Assume the demand forecast is normally distributed with mean 3,192 and standard deviation 1,181. Recall, O'Neill's optimal first order is 3,263 and O'Neill's expected second order is 437 units.
c. What is TEC's optimal first production quantity if its CEO authorizes its production manager to choose a quantity that is greater than O'Neill's first order?
d. Given the order chosen in part c, what is TEC's expected profit? (Warning: this is a hard question.)

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
11
(Parkas) A firm sells five women's ski parkas. Some data on those parkas are listed below:
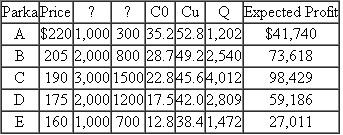 Q in the above table is the optimal newsvendor quantity and "Expected Profit" is the news-vendor expected profit if Q is ordered. The firm will produce some parkas well in advance of the selling season. The other parkas are produced after a trade show that occurs shortly before the season starts. After attending the trade show, the firm will basically know demand for each parka. Unfortunately, the firm's capacity is limited after the trade show, so the firm wants to produce at least 5,000 parkas before the trade show. Furthermore, a parka should be produced either before the trade show or after the trade show, but a parka should not be produced in both production opportunities.
Q in the above table is the optimal newsvendor quantity and "Expected Profit" is the news-vendor expected profit if Q is ordered. The firm will produce some parkas well in advance of the selling season. The other parkas are produced after a trade show that occurs shortly before the season starts. After attending the trade show, the firm will basically know demand for each parka. Unfortunately, the firm's capacity is limited after the trade show, so the firm wants to produce at least 5,000 parkas before the trade show. Furthermore, a parka should be produced either before the trade show or after the trade show, but a parka should not be produced in both production opportunities.
a. What is the firm's expected profit if every parka is produced before the trade show?
b. What is the firm's expected profit if every parka is produced after the trade show?
c. What should the production quantities before the trade show be for each parka?
d. What is the expected number of units the firm will produce after the trade show? (Assume that there is sufficient after-trade show capacity given the before-trade show order.)
e. What is the firm's expected profit?
 Q in the above table is the optimal newsvendor quantity and "Expected Profit" is the news-vendor expected profit if Q is ordered. The firm will produce some parkas well in advance of the selling season. The other parkas are produced after a trade show that occurs shortly before the season starts. After attending the trade show, the firm will basically know demand for each parka. Unfortunately, the firm's capacity is limited after the trade show, so the firm wants to produce at least 5,000 parkas before the trade show. Furthermore, a parka should be produced either before the trade show or after the trade show, but a parka should not be produced in both production opportunities.
Q in the above table is the optimal newsvendor quantity and "Expected Profit" is the news-vendor expected profit if Q is ordered. The firm will produce some parkas well in advance of the selling season. The other parkas are produced after a trade show that occurs shortly before the season starts. After attending the trade show, the firm will basically know demand for each parka. Unfortunately, the firm's capacity is limited after the trade show, so the firm wants to produce at least 5,000 parkas before the trade show. Furthermore, a parka should be produced either before the trade show or after the trade show, but a parka should not be produced in both production opportunities.a. What is the firm's expected profit if every parka is produced before the trade show?
b. What is the firm's expected profit if every parka is produced after the trade show?
c. What should the production quantities before the trade show be for each parka?
d. What is the expected number of units the firm will produce after the trade show? (Assume that there is sufficient after-trade show capacity given the before-trade show order.)
e. What is the firm's expected profit?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
12
(Office Supply Company) Office Supply Company (OSC) has a spare parts warehouse in Alaska to support its office equipment maintenance needs. Once every six months, a major replenishment shipment is received. If the inventory of any given part runs out before the next replenishment, then emergency air shipments are used to resupply the part as needed. Orders are placed on January 15 and June 15, and orders are received on February 15 and July 15, respectively.
OSC must determine replenishment quantities for its spare parts. As an example, historical data show that total demand for part 1AA-66 over a six-month interval is Poisson with mean 6.5. The cost of inventorying the unneeded part for six months is $5 (which includes both physical and financial holding costs and is charged based on inventory at the end of the six-month period). The variable production cost for 1AA-66 is $37 per part. The cost of a regular, semiannual shipment is $32 per part, and the cost of an emergency shipment is $50 per part.
It is January 15 and there are currently three 1AA-66 parts in inventory. How many parts should arrive on February 15?
OSC must determine replenishment quantities for its spare parts. As an example, historical data show that total demand for part 1AA-66 over a six-month interval is Poisson with mean 6.5. The cost of inventorying the unneeded part for six months is $5 (which includes both physical and financial holding costs and is charged based on inventory at the end of the six-month period). The variable production cost for 1AA-66 is $37 per part. The cost of a regular, semiannual shipment is $32 per part, and the cost of an emergency shipment is $50 per part.
It is January 15 and there are currently three 1AA-66 parts in inventory. How many parts should arrive on February 15?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
13
(Steve Smith) Steve Smith is a car sales agent at a Ford dealership. He earns a salary and benefits, but a large portion of his income comes from commissions: $350 per vehicle sold for the first five vehicles in a month and $400 per vehicle after that. Steve's historical sales can be well described with a Poisson distribution with mean 5.5; that is, on average, Steve sells 5.5 vehicles per month. On average, how much does Steve earn in commissions per month?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck



