Deck 33: The Nature and Propagation of Light
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/31
Play
Full screen (f)
Deck 33: The Nature and Propagation of Light
1
Molecular rotation: A rotating diatomic molecule in its l = 1 quantum state has energy E. What is the energy of the same molecule in its l = 2 quantum state?
A) 2E
B) 3E
C) 4E
D) 6E
E) 8E
A) 2E
B) 3E
C) 4E
D) 6E
E) 8E
3E
2
Semiconductors: An unfilled electron state in the valence band is called
A) a hole.
B) an empty electron.
C) a conduction electron.
D) a positron.
E) an empty positron.
A) a hole.
B) an empty electron.
C) a conduction electron.
D) a positron.
E) an empty positron.
a hole.
3
Molecular rotation: Estimate the rotational energy (in eV) for a diatomic hydrogen molecule in the l = 2 quantum state. (The equilibrium separation for the H2 molecule is 0.074 nm.) (1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, mh ≈ mproton = 1.67 × 10-27 kg)
A) 0.011 eV
B) 0.026 eV
C) 0.032 eV
D) 0.046 eV
E) 0.055 eV
A) 0.011 eV
B) 0.026 eV
C) 0.032 eV
D) 0.046 eV
E) 0.055 eV
0.046 eV
4
Molecular vibration: The vibrational frequency of an HF molecule is 8.72 × 1013 Hz and the reduced mass of the molecule is 1.589 × 10-27 kg. What is the ground state vibrational energy of an HF molecule? (1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 0.12 eV
B) 0.18 eV
C) 0.24 eV
D) 0.30 eV
E) 0.36 eV
A) 0.12 eV
B) 0.18 eV
C) 0.24 eV
D) 0.30 eV
E) 0.36 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
5
Molecular rotation: A rotating diatomic molecule has rotational quantum number l. The energy DIFFERENCE between adjacent energy levels
A) increases as l increases.
B) decreases as l increases.
C) is the same for all changes in l.
D) is independent of l.
A) increases as l increases.
B) decreases as l increases.
C) is the same for all changes in l.
D) is independent of l.

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
6
Molecular rotation: A diatomic molecule has 18 × 10-5 eV of rotational energy in the l = 2 quantum state. What is its rotational energy in the l = 0 quantum state?
A) 90 µeV
B) 60 µeV
C) 30 µeV
D) 15 µeV
E) 0 eV
A) 90 µeV
B) 60 µeV
C) 30 µeV
D) 15 µeV
E) 0 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
7
Molecular vibration: A vibrating diatomic molecule has vibrational quantum number n. The energy DIFFERENCE between adjacent energy levels
A) increases as n increases.
B) decreases as n increases.
C) is the same for all changes in n.
D) is independent of n.
A) increases as n increases.
B) decreases as n increases.
C) is the same for all changes in n.
D) is independent of n.

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
8
Molecular rotation: The moment of inertia of a fluorine ( 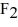 ) molecule is
) molecule is 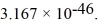 What is the rotational energy of a fluorine molecule for the l = 19 state? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
What is the rotational energy of a fluorine molecule for the l = 19 state? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
A) 4.2 × 10-2 eV
B) 2.1 × 10-3 eV
C) 4.6 × 10-2 eV
D) 5.1 × 10-2 eV
E) 5.6 × 10-2 eV
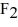 ) molecule is
) molecule is 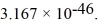 What is the rotational energy of a fluorine molecule for the l = 19 state? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
What is the rotational energy of a fluorine molecule for the l = 19 state? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)A) 4.2 × 10-2 eV
B) 2.1 × 10-3 eV
C) 4.6 × 10-2 eV
D) 5.1 × 10-2 eV
E) 5.6 × 10-2 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
9
Molecular rotation: A diatomic molecule has 2.6 × 10-5 eV of rotational energy in the l = 2 quantum state. What is its rotational energy in the l = 1 quantum state?
A) 3.4 µeV
B) 4.1 µeV
C) 5.3 µeV
D) 7.8 µeV
E) 8.7 µeV
A) 3.4 µeV
B) 4.1 µeV
C) 5.3 µeV
D) 7.8 µeV
E) 8.7 µeV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
10
Molecular bonds: Covalent bonding is due to
A) the sharing of electrons between atoms.
B) the transfer of electrons between atoms.
C) atoms bonding to hydrogen molecules.
D) atoms bonding to oxygen molecules.
A) the sharing of electrons between atoms.
B) the transfer of electrons between atoms.
C) atoms bonding to hydrogen molecules.
D) atoms bonding to oxygen molecules.

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
11
Molecular rotation: A certain molecule has 2.00 eV of rotational energy in the l = 1 state. In the l = 4 state, what would its rotational energy be?
A) 8.00 eV
B) 16.0 eV
C) 20.0 eV
D) 30.0 eV
E) 32.0 eV
A) 8.00 eV
B) 16.0 eV
C) 20.0 eV
D) 30.0 eV
E) 32.0 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
12
Molecular rotation: A diatomic molecule has a moment of inertia of 7.73 × 10-45 kg∙ m2. What is its rotational energy in the quantum state characterized by l = 2? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
A) 22.7 µeV
B) 27.0 µeV
C) 587 µeV
D) 72.2 µeV
E) 87.1 µeV
A) 22.7 µeV
B) 27.0 µeV
C) 587 µeV
D) 72.2 µeV
E) 87.1 µeV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
13
Molecular rotation: The spacing of the atoms (treated as point masses) in the H2 molecule is 7.4 × 10-11 m. What is the energy of the l = 1 rotational level? (1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, mh ≈ mproton = 1.67 × 10-27 kg)
A) 0.090 eV
B) 0.070 eV
C) 0.045 eV
D) 0.030 eV
E) 0.015 eV
A) 0.090 eV
B) 0.070 eV
C) 0.045 eV
D) 0.030 eV
E) 0.015 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
14
Molecular rotation: When a certain diatomic molecule undergoes a transition from the l = 5 to the l = 3 rotational level, the emitted photon has wavelength 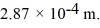 Calculate the moment of inertia of the molecule. (c = 3.00 × 108 m/s, e = 1.60 × 10-19 C, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s)
Calculate the moment of inertia of the molecule. (c = 3.00 × 108 m/s, e = 1.60 × 10-19 C, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s)
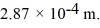 Calculate the moment of inertia of the molecule. (c = 3.00 × 108 m/s, e = 1.60 × 10-19 C, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s)
Calculate the moment of inertia of the molecule. (c = 3.00 × 108 m/s, e = 1.60 × 10-19 C, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s)
Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
15
Molecular bonds: Ionic bonding is due to
A) the sharing of electrons between atoms.
B) the transfer of electrons between atoms.
C) atoms bonding to hydrogen molecules.
D) atoms bonding to oxygen molecules.
A) the sharing of electrons between atoms.
B) the transfer of electrons between atoms.
C) atoms bonding to hydrogen molecules.
D) atoms bonding to oxygen molecules.

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
16
Semiconductors: In a p-type semiconductor, a hole is
A) a donor atom.
B) an extra electron supplied by a donor atom.
C) an extra proton supplied by a donor atom.
D) a missing atom in the crystalline structure.
E) a region where an electron is missing.
A) a donor atom.
B) an extra electron supplied by a donor atom.
C) an extra proton supplied by a donor atom.
D) a missing atom in the crystalline structure.
E) a region where an electron is missing.

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
17
Molecular vibration: A vibrating diatomic molecule in its ground state has energy E. What is the energy of the same molecule in its second EXCITED state?
A) E
B) 2E
C) 3E
D) 5E
E) 9E
A) E
B) 2E
C) 3E
D) 5E
E) 9E

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
18
Molecular vibration: A certain diatomic molecule emits a photon of energy 1.20 eV when it makes a transition from the n = 1 vibrational state to the next lower vibrational state. What is the frequency of vibration of the molecule? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
A) 1.93 × 1014 Hz
B) 2.90 × 1014 Hz
C) 4.35 × 1014 Hz
D) 1.82 × 1015 Hz
E) 2.73 × 1015 Hz
A) 1.93 × 1014 Hz
B) 2.90 × 1014 Hz
C) 4.35 × 1014 Hz
D) 1.82 × 1015 Hz
E) 2.73 × 1015 Hz

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
19
Molecular vibration: A diatomic molecule is vibrating in its first excited quantum state above the ground state. In that excited state, its frequency is 2.0 × 1013 Hz. What is the energy of the molecule in this state? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J
A) 0.041 eV
B) 0.083 eV
C) 0.12 eV
D) 0.15 eV
E) 0.17 eV
A) 0.041 eV
B) 0.083 eV
C) 0.12 eV
D) 0.15 eV
E) 0.17 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
20
Semiconductors: A p-type semiconductor has a net positive charge.

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
21
Molecular vibration: A certain diatomic molecule emits a photon of energy 1.20 eV when it makes a transition from the n = 1 vibrational state to the next lower vibrational state. If the molecule made a transition from the n = 2 state to the n = 1 state, what would be the energy of the photon it would emit? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
A) 3.60 eV
B) 2.40 eV
C) 1.20 eV
D) 0.60 eV
E) 0.30 eV
A) 3.60 eV
B) 2.40 eV
C) 1.20 eV
D) 0.60 eV
E) 0.30 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
22
Free-electron theory of metals: The Fermi energy of rubidium at a temperature of 5 K is 1.85 eV. An electron state in rubidium is 0.007 eV above the Fermi level. What is the probability that this state is occupied at a temperature of 9K? (mel = 9.11 × 10-31 kg, h = 6.626 × 10-34 J ∙ s, Boltzmann constant = 1.38 ∙ 10-23 J/K, 1 eV = 1.60 × 10-19 J)
A) 1 × 10-4
B) 2 × 10-5
C) 5 × 10-6
D) 1 × 10-6
E) 2 × 10-7
A) 1 × 10-4
B) 2 × 10-5
C) 5 × 10-6
D) 1 × 10-6
E) 2 × 10-7

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
23
Semiconductors: The energy gap between the valence and conduction bands in a certain semiconductor is 1.25 eV. What is the threshold wavelength for optical absorption in this substance? (c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s)
A) 599 nm
B) 639 nm
C) 959 nm
D) 873 nm
E) 994 nm
A) 599 nm
B) 639 nm
C) 959 nm
D) 873 nm
E) 994 nm

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
24
Free-electron theory of metals: If a metal had a Fermi level (energy) of 5.0 eV, what would be the average energy of the electrons at 0 K?
A) 8.0 eV
B) 6.0 eV
C) 3.0 eV
D) 0.00 eV
E) 5.0 eV
A) 8.0 eV
B) 6.0 eV
C) 3.0 eV
D) 0.00 eV
E) 5.0 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
25
Free-electron theory of metals: If one metal has double the number of conduction electrons per unit volume of a second metal, then its Fermi level (energy) is how many times that of the second metal?
A) 1.41
B) 2.83
C) 2.00
D) 3.22
E) 1.59
A) 1.41
B) 2.83
C) 2.00
D) 3.22
E) 1.59

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
26
Free-electron theory of metals: A metal has a Fermi level (energy) of 5.50 eV. At 1200 K, what energy will have a 90% occupancy probability? (mel = 9.11 × 10-31 kg, h = 6.626 × 10-34 J ∙ s, Boltzmann constant = 1.38 × 10-23, 1 eV = 1.60 × 10-19 J)
A) 5.79 eV
B) 5.73 eV
C) 5.56 eV
D) 5.44 eV
E) 5.27 eV
A) 5.79 eV
B) 5.73 eV
C) 5.56 eV
D) 5.44 eV
E) 5.27 eV

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
27
Free-electron theory of metals: For a solid in which the occupation of the energy states is given by the Fermi-Dirac distribution, the probability that a certain state is occupied at a temperature T0 is 0.70. If the temperature is doubled to 2T0, what is the probability that the same state is occupied? Assume that the Fermi energy does not change with temperature.

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
28
Free-electron theory of metals: Silver has a Fermi level (energy) of 5.5 eV. At 0 K, at what speed would the electrons be moving if they had kinetic energy equal to the Fermi energy? (This speed is known as the Fermi speed.) (mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s)
A) 1400 km/s
B) 1.0 km/s
C) 2.2 km/s
D) 1100 km/s
E) 3.5 km/s
A) 1400 km/s
B) 1.0 km/s
C) 2.2 km/s
D) 1100 km/s
E) 3.5 km/s

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
29
Free-electron theory of metals: What is the occupancy probability at an energy of 12.00 eV for a material with a Fermi energy (level) of 11.63 eV at a temperature of 500 K? (mel = 9.11 × 10-31 kg, h = 6.626 × 10-34 J ∙ s, Boltzmann constant = 1.38 × 10-23, 1 eV = 1.60 × 10-19 J)
A) 0.00030%
B) 0.019%
C) 2.0%
D) 6.0%
E) 12%
A) 0.00030%
B) 0.019%
C) 2.0%
D) 6.0%
E) 12%

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
30
Free-electron theory of metals: The Fermi level (energy) of a metal is 5.5 eV. What is the number of conduction electrons per unit volume for this metal? (mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J, h = 6.626 × 10-34 J ∙ s)
A) 5.8 × 1028 / m3
B) 6.2 × 1028 / m3
C) 4.1 × 1028 / m3
D) 8.4 × 1028 / m3
E) 3.3 × 1028 / m3
A) 5.8 × 1028 / m3
B) 6.2 × 1028 / m3
C) 4.1 × 1028 / m3
D) 8.4 × 1028 / m3
E) 3.3 × 1028 / m3

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck
31
Density of states: Approximately how many states in the range from 5.0 eV to 5.2 eV are there in a copper bar of volume 5.3 cm3? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
A) 5.1 × 1022
B) 3.2 × 1022
C) 1.6 × 1022
D) 8.2 × 1021
E) 3.2 × 1021
A) 5.1 × 1022
B) 3.2 × 1022
C) 1.6 × 1022
D) 8.2 × 1021
E) 3.2 × 1021

Unlock Deck
Unlock for access to all 31 flashcards in this deck.
Unlock Deck
k this deck



