Deck 5: Elements of Airplane Performance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/38
Play
Full screen (f)
Deck 5: Elements of Airplane Performance
1
Consider an airplane patterned after the twin-engine Beechcraft Queen Air executive transport. The airplane weight is 38,220 N, wing area is 27.3 m 2 , aspect ratio is 7.5, Oswald efficiency factor is 0.9, and zero-lift drag coefficient is C D ,0 = 0.03. Calculate the thrust required to fly at a velocity of 350 km/h at ( a ) standard sea level and ( b ) an altitude of 4.5 km.
The standard sea level gives a set of conditions for the physical calculations. The value of air density at the sea level condition is
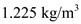 . As the altitude changes the density of air also changes. At the altitude of
. As the altitude changes the density of air also changes. At the altitude of
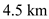 the value of air density is
the value of air density is
 .
.
(a)
Write the expression for the lift polar coefficient of the airplane as follows:
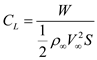 …… (1)
…… (1)
Here,
 is the air density,
is the air density,
 is the velocity of the airplane for a given altitude and
is the velocity of the airplane for a given altitude and
 is the wing area.
is the wing area.
Substitute the values of
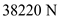 for
for
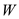 ,
,
 for
for
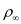 ,
,
 for
for
 ,
,
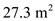 for
for
 in the equation (1).
in the equation (1).
 Write the expression for drag polar coefficient as follows;
Write the expression for drag polar coefficient as follows;
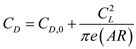 …… (2)
…… (2)
Here,
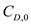 is the zero-lift drag coefficient,
is the zero-lift drag coefficient,
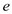 is the Oswald's efficiency factor and
is the Oswald's efficiency factor and
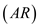 is the aspect ratio.
is the aspect ratio.
Substitute the value of
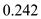 for
for
 ,
,
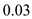 for
for
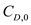 ,
,
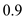 for
for
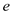 and
and
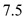 for
for
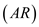 in the equation (2).
in the equation (2).
 Write the expression for the thrust acting on an airplane.
Write the expression for the thrust acting on an airplane.
 …… (3)
…… (3)
Here,
 is the required thrust,
is the required thrust,
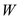 is the weight of the airplane,
is the weight of the airplane,
 is the lift polar coefficient of the airplane and
is the lift polar coefficient of the airplane and
 is the drag polar coefficient of the plane.
is the drag polar coefficient of the plane.
Substitute
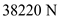 for
for
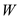 ,
,
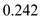 for
for
 and
and
 for
for
 in the equation (3).
in the equation (3).
 Hence, the required value of thrust at standard sea level is
Hence, the required value of thrust at standard sea level is
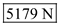 .
.
(b)
Calculate lift polar coefficient of the airplane at the height of
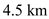 .
.
Substitute the values of
 for
for
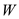 ,
,
 for
for
 ,
,
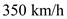 for
for
 ,
,
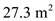 for
for
 in the equation (1).
in the equation (1).
 Substitute the value of
Substitute the value of
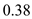 for
for
 ,
,
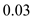 for
for
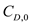 ,
,
 for
for
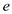 and
and
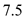 for
for
 in the equation (2).
in the equation (2).
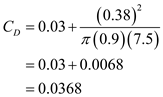 Substitute
Substitute
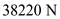 for
for
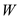 ,
,
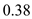 for
for
 and
and
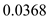 for
for
 in the equation (3).
in the equation (3).
 Hence, the required value of thrust at the altitude of
Hence, the required value of thrust at the altitude of
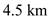 is
is
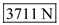 .
.
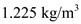 . As the altitude changes the density of air also changes. At the altitude of
. As the altitude changes the density of air also changes. At the altitude of 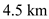 the value of air density is
the value of air density is .
.(a)
Write the expression for the lift polar coefficient of the airplane as follows:
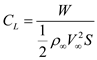 …… (1)
…… (1)Here,
 is the air density,
is the air density,  is the velocity of the airplane for a given altitude and
is the velocity of the airplane for a given altitude and  is the wing area.
is the wing area.Substitute the values of
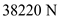 for
for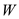 ,
,  for
for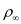 ,
,  for
for ,
, 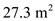 for
for  in the equation (1).
in the equation (1). Write the expression for drag polar coefficient as follows;
Write the expression for drag polar coefficient as follows;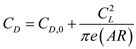 …… (2)
…… (2)Here,
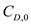 is the zero-lift drag coefficient,
is the zero-lift drag coefficient, 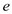 is the Oswald's efficiency factor and
is the Oswald's efficiency factor and 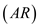 is the aspect ratio.
is the aspect ratio.Substitute the value of
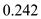 for
for ,
, 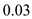 for
for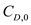 ,
, 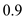 for
for 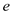 and
and 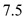 for
for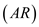 in the equation (2).
in the equation (2). Write the expression for the thrust acting on an airplane.
Write the expression for the thrust acting on an airplane. …… (3)
…… (3)Here,
 is the required thrust,
is the required thrust, 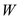 is the weight of the airplane,
is the weight of the airplane,  is the lift polar coefficient of the airplane and
is the lift polar coefficient of the airplane and  is the drag polar coefficient of the plane.
is the drag polar coefficient of the plane.Substitute
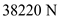 for
for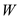 ,
, 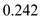 for
for  and
and  for
for  in the equation (3).
in the equation (3). Hence, the required value of thrust at standard sea level is
Hence, the required value of thrust at standard sea level is 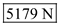 .
. (b)
Calculate lift polar coefficient of the airplane at the height of
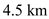 .
.Substitute the values of
 for
for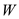 ,
,  for
for ,
, 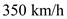 for
for ,
, 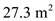 for
for 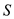 in the equation (1).
in the equation (1).  Substitute the value of
Substitute the value of 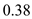 for
for ,
, 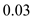 for
for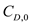 ,
,  for
for 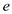 and
and 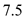 for
for 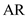 in the equation (2).
in the equation (2).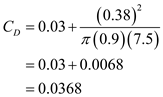 Substitute
Substitute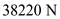 for
for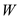 ,
, 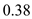 for
for  and
and 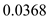 for
for  in the equation (3).
in the equation (3).  Hence, the required value of thrust at the altitude of
Hence, the required value of thrust at the altitude of 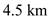 is
is 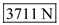 .
. 2
An airplane weighing 5000 lb is flying at standard sea level with a velocity of 200 mi/h. At this velocity the L/D ratio is a maximum. The wing area and aspect ratio are 200 ft 2 and 8.5, respectively. The Oswald efficiency factor is 0.93. Calculate the total drag on the airplane.
Total drag of an airplane is defined as the summation of zero lift drag and the drag due to lift. The corresponding drag coefficients are
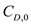 and
and
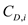 respectively.
respectively.
Write the expression for the total drag is,
 ...... (1)
...... (1)
Here,
 is the dynamic pressure,
is the dynamic pressure,
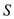 is the area of the wing,
is the area of the wing,
 is the coefficient of zero lift drag and
is the coefficient of zero lift drag and
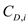 is the coefficient of drag due to lift.
is the coefficient of drag due to lift.
Since the airplane is flying at the maximum
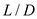 condition. Thus, the minimum thrust required is expressed by following equation.
condition. Thus, the minimum thrust required is expressed by following equation.
 Hence, the expression for the total drag is,
Hence, the expression for the total drag is,
 …… (2)
…… (2)
Write the expression for the dynamic pressure
 as follows;
as follows;
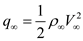 …… (3)
…… (3)
Here,
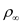 is the air density at the level and
is the air density at the level and
 is the velocity of the airplane.
is the velocity of the airplane.
Write the expression for the coefficient of drag due to lift
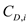 as follows;
as follows;
 …… (4)
…… (4)
Here,
 is the lift polar coefficient of the airplane,
is the lift polar coefficient of the airplane,
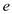 is the Oswald efficiency factor and
is the Oswald efficiency factor and
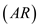 is the aspect ratio of the airplane.
is the aspect ratio of the airplane.
Write the expression for the lift polar coefficient of the airplane
 as follows;
as follows;
 …… (5)
…… (5)
Here,
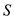 is the wing area,
is the wing area,
 is the dynamic pressure and
is the dynamic pressure and
 is the weight of the plane.
is the weight of the plane.
Calculate the value of dynamic pressure.
Substitute
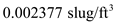 for
for
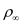 ,
,
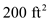 for
for
 in equation (3).
in equation (3).
 Calculate the lift polar coefficient.
Calculate the lift polar coefficient.
Substitute
 for
for
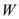 ,
,
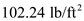 for
for
 and
and
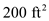 for
for
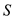 in the equation (5).
in the equation (5).
 Again, calculate the coefficient of drag due to lift.
Again, calculate the coefficient of drag due to lift.
Substitute
 for
for
 ,
,
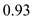 for
for
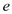 ,
,
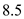 for
for
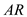 in the equation (4).
in the equation (4).
 Now calculate the total drag.
Now calculate the total drag.
Substitute
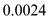 for
for
 ,
,
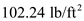 for
for
 and
and
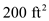 for
for
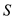 in the equation (2).
in the equation (2).
 Hence, the required total drag on the plane is
Hence, the required total drag on the plane is
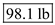 .
.
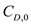 and
and 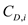 respectively.
respectively. Write the expression for the total drag is,
 ...... (1)
...... (1)Here,
 is the dynamic pressure,
is the dynamic pressure, 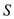 is the area of the wing,
is the area of the wing,  is the coefficient of zero lift drag and
is the coefficient of zero lift drag and 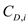 is the coefficient of drag due to lift.
is the coefficient of drag due to lift.Since the airplane is flying at the maximum
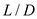 condition. Thus, the minimum thrust required is expressed by following equation.
condition. Thus, the minimum thrust required is expressed by following equation. Hence, the expression for the total drag is,
Hence, the expression for the total drag is,  …… (2)
…… (2)Write the expression for the dynamic pressure
 as follows;
as follows;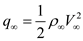 …… (3)
…… (3)Here,
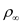 is the air density at the level and
is the air density at the level and  is the velocity of the airplane.
is the velocity of the airplane.Write the expression for the coefficient of drag due to lift
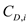 as follows;
as follows; …… (4)
…… (4)Here,
 is the lift polar coefficient of the airplane,
is the lift polar coefficient of the airplane, 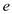 is the Oswald efficiency factor and
is the Oswald efficiency factor and 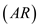 is the aspect ratio of the airplane.
is the aspect ratio of the airplane.Write the expression for the lift polar coefficient of the airplane
 as follows;
as follows; …… (5)
…… (5)Here,
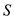 is the wing area,
is the wing area,  is the dynamic pressure and
is the dynamic pressure and  is the weight of the plane.
is the weight of the plane.Calculate the value of dynamic pressure.
Substitute
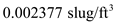 for
for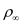 ,
, 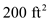 for
for  in equation (3).
in equation (3). Calculate the lift polar coefficient.
Calculate the lift polar coefficient.Substitute
 for
for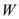 ,
, 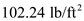 for
for  and
and 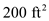 for
for 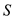 in the equation (5).
in the equation (5). Again, calculate the coefficient of drag due to lift.
Again, calculate the coefficient of drag due to lift.Substitute
 for
for ,
, 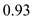 for
for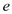 ,
, 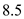 for
for 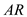 in the equation (4).
in the equation (4). Now calculate the total drag.
Now calculate the total drag.Substitute
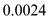 for
for ,
, 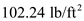 for
for  and
and 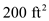 for
for 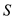 in the equation (2).
in the equation (2). Hence, the required total drag on the plane is
Hence, the required total drag on the plane is 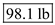 .
. 3
Consider an airplane patterned after the Fairchild Republic A-10, a twin-jet attack aircraft. The airplane has the following characteristics: wing area = 47m 2 , aspect ratio = 6.5, Oswald efficiency factor = 0.87, weight = 103,047N, and zero-lift drag coefficient = 0.032. The airplane is equipped with two jet engines with 40.298 N of static thrust each at sea level.
a. Calculate and plot the power-required curve at sea level.
b. Calculate the maximum velocity at sea level.
c. Calculate and plot the power-required curve at 5-km altitude.
d. Calculate the maximum velocity at 5-km altitude. (Assume the engine thrust varies directly with free-stream density.)
a. Calculate and plot the power-required curve at sea level.
b. Calculate the maximum velocity at sea level.
c. Calculate and plot the power-required curve at 5-km altitude.
d. Calculate the maximum velocity at 5-km altitude. (Assume the engine thrust varies directly with free-stream density.)
The static thrust is defined as such a force which is developed and applied by the jet engine on the surrounding air or earth when the airplane is at rest condition.
Power is defined as the rate of doing work with respect to time. Power is a scalar quantity and having no direction. The unit of power is
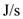 or watt in an hour
or watt in an hour
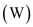 .
.
The expression to calculate the resultant power
 is,
is,
 …… (1)
…… (1)
Here,
 is the required power,
is the required power,
 is the required thrust and
is the required thrust and
 is the velocity of the airplane at a certain altitude.
is the velocity of the airplane at a certain altitude.
The expression for the actual power for two engines is,
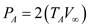 …… (2)
…… (2)
Here,
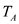 is the actual thrust and
is the actual thrust and
 is the velocity of the airplane for a given altitude.
is the velocity of the airplane for a given altitude.
Write the expression for the thrust of an airplane.
 …… (3)
…… (3)
Here,
 is the required thrust,
is the required thrust,
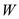 is the weight of the airplane,
is the weight of the airplane,
 is the lift polar coefficient of the airplane and
is the lift polar coefficient of the airplane and
 is the drag polar coefficient of the plane.
is the drag polar coefficient of the plane.
Write the expression for the lift polar coefficient of the airplane.
 …… (4)
…… (4)
Here,
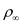 is the air density,
is the air density,
 is the velocity of the airplane for a given altitude and
is the velocity of the airplane for a given altitude and
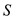 is the wing area.
is the wing area.
Write the expression for drag polar coefficient.
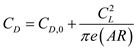 …… (5)
…… (5)
Here,
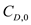 is the zero-lift drag coefficient,
is the zero-lift drag coefficient,
 is the Oswald's efficiency factor and
is the Oswald's efficiency factor and
 is the aspect ratio.
is the aspect ratio.
(a)
Consider the velocity of the airplane is,
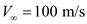 .
.
Calculate the lift polar coefficient of the airplane.
Substitute
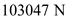 for
for
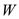 ,
,
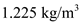 for
for
 ,
,
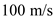 for
for
 ,
,
 for
for
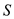 in the equation (4).
in the equation (4).
 Calculate the drag polar coefficient.
Calculate the drag polar coefficient.
Substitute
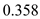 for
for
 ,
,
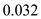 for
for
 ,
,
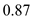 for
for
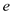 and
and
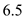 for
for
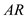 in the equation (5).
in the equation (5).
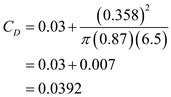 Similarly, calculate the thrust of an airplane.
Similarly, calculate the thrust of an airplane.
Substitute
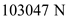 for
for
 ,
,
 for
for
 and
and
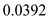 for
for
 in the equation (3).
in the equation (3).
 Calculate the resultant power
Calculate the resultant power
 .
.
Substitute
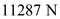 for
for
 and
and
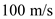 for
for
 in the expression of resultant power
in the expression of resultant power
 in the equation (1).
in the equation (1).
 Tabulate a few different velocities as follows:
Tabulate a few different velocities as follows:
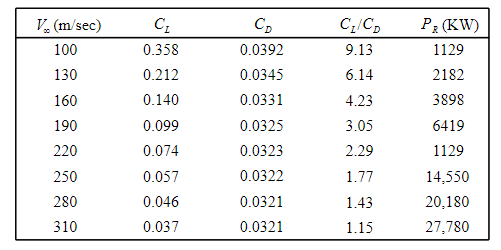 Calculate the actual power for two engines.
Calculate the actual power for two engines.
Substitute
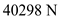 for
for
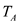 and
and
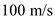 for
for
 in the equation (2).
in the equation (2).
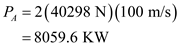 Hence, the required value of the actual power for two jet engines at the sea level is
Hence, the required value of the actual power for two jet engines at the sea level is
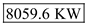 .
.
Draw the curve of power required at sea level as follows;
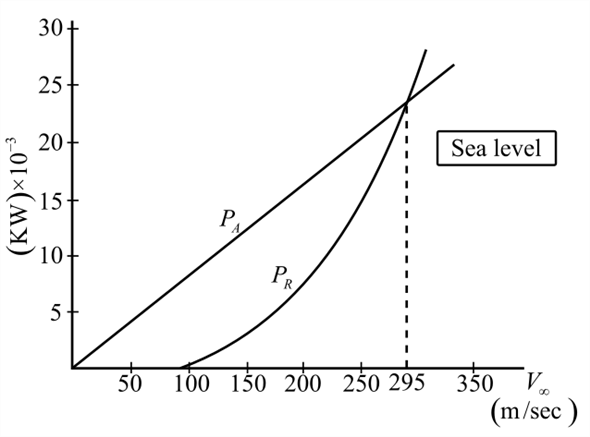 (b)
(b)
Calculate the maximum velocity at the sea level from the above graph of power required at sea level.
It is clear that maximum velocity
 is,
is,
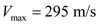 Hence, the maximum velocity at the sea level is
Hence, the maximum velocity at the sea level is
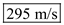 .
.
(c)
The intersection points of resultant power and actual power gives the maximum velocity at the sea level.
The density of air changes with respect to the level of altitude from the sea level. Therefore, the standard value of air density at the altitude of
 is
is
 .
.
The expression of the altitude effect on the velocity as follows;
 …… (6)
…… (6)
Here,
 is the velocity at the sea level,
is the velocity at the sea level,
 is the air density at the sea level
is the air density at the sea level
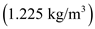 and
and
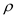 the density of air at the certain altitude.
the density of air at the certain altitude.
The expression of the altitude effect on the required power as follows;
 …… (7)
…… (7)
Here,
 is the required power at given level.
is the required power at given level.
Calculate the altitude effect on the velocity.
Substitute the value of
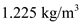 for
for
 and
and
 for
for
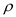 in the equation (6),
in the equation (6),
 Similarly, calculate the altitude effect on the required power.
Similarly, calculate the altitude effect on the required power.
Substitute the value of
 for
for
 and
and
 for
for
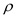 in the equation (7),
in the equation (7),
 Tabulate the few different values of
Tabulate the few different values of
 ,
,
 ,
,
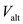 and
and
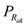 . Write all the calculate values in tabular form as shown below.
. Write all the calculate values in tabular form as shown below.
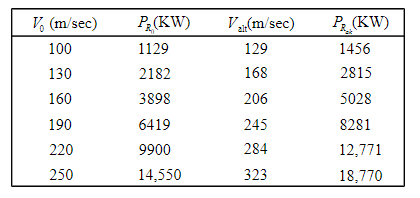 Draw the curve between
Draw the curve between
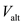 and
and
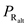 as follows;
as follows;
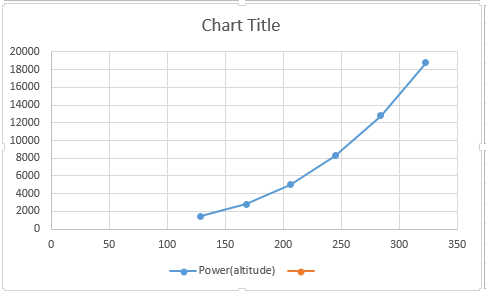 (d)
(d)
Calculate the total thrust generated by both engines as follows:
Total thrust generated by both engines is expressed by the following equation.
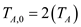 Here,
Here,
 is the thrust generated by one engine.
is the thrust generated by one engine.
The expression for the actual thrust at the certain altitude
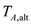 is,
is,
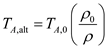 …… (8)
…… (8)
Here,
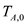 is the thrust of the airplane of two jet engine at the sea level
is the thrust of the airplane of two jet engine at the sea level
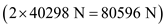 .
.
Write the expression of the power at given altitude is,
 …… (9)
…… (9)
Calculate the actual thrust at the altitude of
 .
.
Substitute
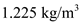 for
for
 and
and
 for
for
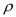 in the equation (8),
in the equation (8),
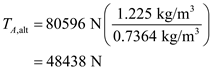 Calculate the actual power at the altitude of
Calculate the actual power at the altitude of
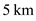 .
.
Substitute the value of
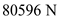 for
for
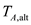 in the equation (9),
in the equation (9),
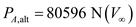 …… (10)
…… (10)
Draw the curve between
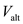 and
and
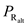 with the help of equation (10) as follows;
with the help of equation (10) as follows;
 It is clear from the power required curve that maximum velocity at the altitude at
It is clear from the power required curve that maximum velocity at the altitude at
 is
is
Hence, the required maximum velocity at the altitude of
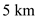 is
is
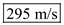 .
.
Power is defined as the rate of doing work with respect to time. Power is a scalar quantity and having no direction. The unit of power is
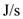 or watt in an hour
or watt in an hour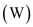 .
.The expression to calculate the resultant power
 is,
is, …… (1)
…… (1)Here,
 is the required power,
is the required power,  is the required thrust and
is the required thrust and  is the velocity of the airplane at a certain altitude.
is the velocity of the airplane at a certain altitude.The expression for the actual power for two engines is,
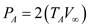 …… (2)
…… (2)Here,
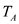 is the actual thrust and
is the actual thrust and  is the velocity of the airplane for a given altitude.
is the velocity of the airplane for a given altitude.Write the expression for the thrust of an airplane.
 …… (3)
…… (3)Here,
 is the required thrust,
is the required thrust, 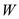 is the weight of the airplane,
is the weight of the airplane,  is the lift polar coefficient of the airplane and
is the lift polar coefficient of the airplane and  is the drag polar coefficient of the plane.
is the drag polar coefficient of the plane.Write the expression for the lift polar coefficient of the airplane.
 …… (4)
…… (4)Here,
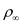 is the air density,
is the air density,  is the velocity of the airplane for a given altitude and
is the velocity of the airplane for a given altitude and 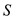 is the wing area.
is the wing area.Write the expression for drag polar coefficient.
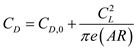 …… (5)
…… (5)Here,
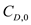 is the zero-lift drag coefficient,
is the zero-lift drag coefficient,  is the Oswald's efficiency factor and
is the Oswald's efficiency factor and  is the aspect ratio.
is the aspect ratio.(a)
Consider the velocity of the airplane is,
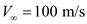 .
.Calculate the lift polar coefficient of the airplane.
Substitute
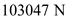 for
for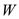 ,
, 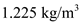 for
for ,
, 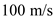 for
for ,
,  for
for 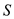 in the equation (4).
in the equation (4). Calculate the drag polar coefficient.
Calculate the drag polar coefficient.Substitute
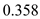 for
for ,
, 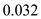 for
for ,
, 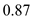 for
for 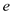 and
and 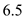 for
for 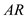 in the equation (5).
in the equation (5).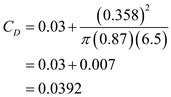 Similarly, calculate the thrust of an airplane.
Similarly, calculate the thrust of an airplane.Substitute
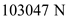 for
for ,
,  for
for  and
and 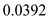 for
for  in the equation (3).
in the equation (3). Calculate the resultant power
Calculate the resultant power .
.Substitute
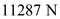 for
for  and
and 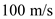 for
for  in the expression of resultant power
in the expression of resultant power  in the equation (1).
in the equation (1). Tabulate a few different velocities as follows:
Tabulate a few different velocities as follows:  Calculate the actual power for two engines.
Calculate the actual power for two engines.Substitute
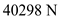 for
for  and
and 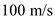 for
for  in the equation (2).
in the equation (2).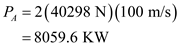 Hence, the required value of the actual power for two jet engines at the sea level is
Hence, the required value of the actual power for two jet engines at the sea level is 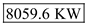 .
. Draw the curve of power required at sea level as follows;
 (b)
(b)Calculate the maximum velocity at the sea level from the above graph of power required at sea level.
It is clear that maximum velocity
 is,
is,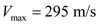 Hence, the maximum velocity at the sea level is
Hence, the maximum velocity at the sea level is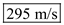 .
.(c)
The intersection points of resultant power and actual power gives the maximum velocity at the sea level.
The density of air changes with respect to the level of altitude from the sea level. Therefore, the standard value of air density at the altitude of
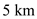 is
is .
.The expression of the altitude effect on the velocity as follows;
 …… (6)
…… (6)Here,
 is the velocity at the sea level,
is the velocity at the sea level,  is the air density at the sea level
is the air density at the sea level 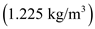 and
and 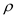 the density of air at the certain altitude.
the density of air at the certain altitude.The expression of the altitude effect on the required power as follows;
 …… (7)
…… (7)Here,
 is the required power at given level.
is the required power at given level.Calculate the altitude effect on the velocity.
Substitute the value of
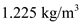 for
for  and
and  for
for 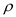 in the equation (6),
in the equation (6), Similarly, calculate the altitude effect on the required power.
Similarly, calculate the altitude effect on the required power.Substitute the value of
 for
for  and
and  for
for 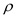 in the equation (7),
in the equation (7), Tabulate the few different values of
Tabulate the few different values of ,
, ,
,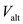 and
and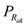 . Write all the calculate values in tabular form as shown below.
. Write all the calculate values in tabular form as shown below.  Draw the curve between
Draw the curve between 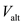 and
and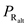 as follows;
as follows; (d)
(d)Calculate the total thrust generated by both engines as follows:
Total thrust generated by both engines is expressed by the following equation.
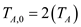 Here,
Here,  is the thrust generated by one engine.
is the thrust generated by one engine.The expression for the actual thrust at the certain altitude
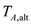 is,
is,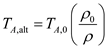 …… (8)
…… (8)Here,
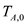 is the thrust of the airplane of two jet engine at the sea level
is the thrust of the airplane of two jet engine at the sea level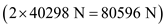 .
.Write the expression of the power at given altitude is,
 …… (9)
…… (9)Calculate the actual thrust at the altitude of
 .
.Substitute
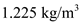 for
for  and
and  for
for 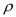 in the equation (8),
in the equation (8),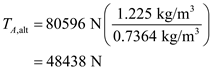 Calculate the actual power at the altitude of
Calculate the actual power at the altitude of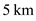 .
.Substitute the value of
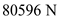 for
for 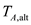 in the equation (9),
in the equation (9),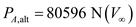 …… (10)
…… (10)Draw the curve between
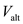 and
and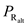 with the help of equation (10) as follows;
with the help of equation (10) as follows; It is clear from the power required curve that maximum velocity at the altitude at
It is clear from the power required curve that maximum velocity at the altitude at  is
is Hence, the required maximum velocity at the altitude of
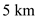 is
is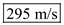 .
. 4
Consider an airplane patterned after the Beechcraft Bonanza V-tailed. single-engine light private airplane. The characteristics of the airplane are as follows: aspect ratio = 6.2, wing area =181 ft 2 , Oswald efficiency factor = 0.91, weight = 3000 lb, and zero-lift drag coefficient = 0.027. The airplane is powered by a single piston engine of 345 hp maximum at sea level. Assume that the power of the engine is proportional to free-stream density. The two-blade propeller has an efficiency of 0.83.
a. Calculate the power required at sea level.
b. Calculate the maximum velocity at sea level.
c. Calculate the power required at 12,000-ft altitude.
d. Calculate the maximum velocity at 12,000-ft altitude.
a. Calculate the power required at sea level.
b. Calculate the maximum velocity at sea level.
c. Calculate the power required at 12,000-ft altitude.
d. Calculate the maximum velocity at 12,000-ft altitude.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
5
From the information generated in Prob. 6.3, calculate the maximum rate of climb for the twin-jet aircraft at sea level and at an altitude of 5 km.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
6
From the information generated in Prob. 6.4, calculate the maximum rate of climb for the single-engine light plane at sea level and at 12,000-ft altitude.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
7
From the rate-of-climb information for the twin-jet aircraft in Prob. 6.5, estimate the absolute ceiling of the airplane. ( Note: Assume maximum R/C varies linearly with altitude-not a precise assumption, but not bad either.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
8
From the rate-of-climb information for the single-engine light plane in Prob. 6.6, estimate the absolute ceiling of the airplane. (Again make the linear assumption described in Prob. 6.7.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
9
The maximum lift-to-drag ratio of the World War I Sopwith Camel was 7.7. If the aircraft is in flight at 5000 ft when the engine fails, how far can it glide in terms of distance measured along the ground?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
10
For the Sopwith Camel in Prob. 6.9, calculate the equilibrium glide velocity at 3000 ft, corresponding to the minimum glide angle. The aspect ratio of the airplane is 4.11, the Oswald efficiency factor is 0.7, the weight is 1400 lb, and the wing area is 231 ft 2.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
11
Consider an airplane with a zero-lift drag coefficient of 0.025, an aspect ratio of 6.72, and an Oswald efficiency factor of 0.9. Calculate the value of ( L / D ) max.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the single-engine light plane described in Prob. 6.4. If the specific fuel consumption is 0.42 lb of fuel per horsepower per hour, the fuel capacity is 44 gal, and the maximum gross weight is 3400 lb, calculate the range and endurance at standard sea level.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
13
Consider the twin-jet airplane described in Prob. 6.3. The thrust-specific fuel consumption is 1.0 N of fuel per newton of thrust per hour, the fuel capacity is 1900 gal, and the maximum gross weight is 136,960 N. Calculate the range and endurance at a standard altitude of 8 km.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
14
Derive Eqs. (6.80) and (6.81).

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
15
Derive Eqs. (6.86) and (6.87).

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
16
Estimate the sea-level liftoff distance for the airplane in Prob. 6.3. Assume a paved runway. Also, during the ground roll, the angle of attack is restricted by the requirement that the tail not drag the ground. Hence, assume that C L , max during the ground roll is limited to 0.8. When the airplane is on the ground, the wings are 5 ft above the ground.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
17
Estimate the sea-level liftoff distance for the airplane in Prob. 6.4. Assume a paved runway, and C L, max = 1.1 during the ground roll. When the airplane is on the ground, the wings are 4 ft above the ground.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
18
Estimate the sea-level landing ground roll distance for the airplane in Prob. 6.3. Assume that the airplane is landing at full gross weight. The maximum lift coefficient with flaps fully employed at touchdown is 2.8. After touchdown, assume zero lift.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
19
Estimate the sea-level landing ground roll distance for the airplane in Prob. 6.4. Assume that the airplane is landing with a weight of 2900 lb. The maximum lift coefficient with flaps at touchdown is 1.8. After touchdown, assume zero lift.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
20
For the airplane in Prob. 6.3, the sea-level comer velocity is 250 mi/h, and the maximum lift coefficient with no flap deflection is 1.2. Calculate the minimum turn radius and maximum turn rate at sea level.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
21
Derive Eq. (6.44).

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
22
From the data shown in Fig. 6.2, estimate the value of the Oswald efficiency factor for the Lockheed C-141A. The wing aspect ratio of the C-141A is 7.9.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
23
Since the end of World War II, various claims have appeared in the popular aviation literature of instances where powerful propeller-driven fighter airplanes from that period have broken the speed of sound in a vertical, power-on dive. The purpose of this problem is to show that such an event is technically not possible. Consider, for example, the Grumman F6F-3 Hellcat, a typical fighter from World War II. For this airplane the zero-lift drag coefficient (at low speeds) is 0.0211, the wing planform area is 334 ft 2 , and the gross weight is 12,441 lb. It is powered by a Pratt and Whitney R-2800 reciprocating engine that, with supercharging to an altitude of 17,500 ft, produces 1500 horsepower. Consider this airplane in a full-power vertical dive at ( a ) 30,000 ft and then ( b ) 20,000 ft. Prove that at these two altitudes the airplane cannot reach Mach 1.
Note: The aerodynamic characteristics of this airplane at Mach 1 have not been measured. So you will have to make some reasonable assumptions. For example, what is the zero-lift drag coefficient at Mach 1? As an estimate, we can obtain from NACA TR 916 a zero-lift drag coefficient for the North American P-51 Mustang, which, when extrapolated to Mach 1, shows an increase of 7.5 over its low-speed value. For the more blunt configuration of the F6F, let us assume that C D ,0 (at M = 1) is 10 times larger than C D ,0 (low speed). Also, at Mach 1 the propeller efficiency would be almost zero (indeed, the propeller might even be producing a net drag rather than any thrust). To be conservative, let us assume the propeller efficiency at Mach 1 to be 0.3.
Note: The aerodynamic characteristics of this airplane at Mach 1 have not been measured. So you will have to make some reasonable assumptions. For example, what is the zero-lift drag coefficient at Mach 1? As an estimate, we can obtain from NACA TR 916 a zero-lift drag coefficient for the North American P-51 Mustang, which, when extrapolated to Mach 1, shows an increase of 7.5 over its low-speed value. For the more blunt configuration of the F6F, let us assume that C D ,0 (at M = 1) is 10 times larger than C D ,0 (low speed). Also, at Mach 1 the propeller efficiency would be almost zero (indeed, the propeller might even be producing a net drag rather than any thrust). To be conservative, let us assume the propeller efficiency at Mach 1 to be 0.3.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
24
The Predator UAV (see Fig. 6.63) has the following characteristics: wingspan = 14,85 m, wing area = 11.45 m 2 , maximum weight = 1020 kg f , and fuel weight = 295 kg f. The power plant is a Rotax four-cylinder, four-stroke engine of 85 horsepower driving a two-blade, variable-pitch pusher propeller. Assume that the Oswald efficiency factor is 0.7, the zero-lift drag coefficient is 0.03, the propeller efficiency is 0.9, and the specific fuel consumption is 0.2 kg f of fuel per horsepower per hour. Calculate the maximum velocity of the Predator at sea level.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
25
For the Predator UAV given in Prob. 6.25, calculate the maximum range.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
26
For the Predator UAV given in Prob. 6.25, calculate the maximum endurance at sea level.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
27
For the special case of an airplane in subsonic steady, level flight, the drag force due to lift, D i , depends directly on the square of the design parameter, W / b , called the span loading , through the relation

Derive this relation.

Derive this relation.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the North American P-51D Mustang shown in Fig. 4.46. Its wingspan is 37 ft, wing area is 233.6 ft 2 , and gross weight is 10,100 lb. Assume that the Oswald efficiency factor is 0.8. The airplane is flying in steady, level flight at a velocity of 300 mph at a standard altitude of 5000 ft. Calculate the drag due to lift using ( a ) the result of Problem 6.28. and ( b ) the coefficient of drag due to lift, C D,i. The two results should be the same.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
29
In the design of a civil jet transport, such as the Boeing 777 shown in Fig. 6.27, the choice of engine size is usually based on having a 300 feet per minute rate-of-climb capability at the top of climb to cruising altitude. This is a safety margin. Assume the following cruise conditions at top of climb for the Boeing 777: L/D = 18, altitude = 31,000 ft, M ? = 0.085, W= 550,000 lb. ( a ) Obtain an equation for the required engine thrust, assuming that the climb angle is so small that L= W. ( b ) Calculate the required engine size (in terms of sea-level static thrust), and compare your result with the designers' engine choice for the Boeing 777, which is two engines of the Rolls-Royce Tront type with a sea-level static thrust of 34,000 lb each.
Note: Intuition might tell you that, for a new airplane design, the engine should be sized to provide enough take off thrust to get the airplane off the ground in a specified take off distance. However, using the top-of-climb criteria discussed here, the resulting engine thrust is usually quite ample for take off.
Note: Intuition might tell you that, for a new airplane design, the engine should be sized to provide enough take off thrust to get the airplane off the ground in a specified take off distance. However, using the top-of-climb criteria discussed here, the resulting engine thrust is usually quite ample for take off.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the Lockheed-Martin F-16 described in Problem 6.31. Assume that the photograph in Fig. 6.56 was taken when the airplane is climbing vertically at the instant it is passing through an altitude of 2000 m with a velocity of 100 m/sec. Calculate the maximum acceleration of the airplane at that instant.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
31
The thrust-specific fuel consumption, TSFC, for a jet engine is defined in Sec. 6.13. Engine manufacturers are constantly trying to reduce TSFC in order to reduce the weight of fuel consumed for a given flight of given time duration. By reducing the fuel weight, the payload weight can be correspondingly increased. However, design changes that result in reductions in TSFC also frequently result in slight increases in the engine weight itself, which will then reduce the payload weight. The break even point is where the decrease in fuel weight is exactly cancelled out by the increase in engine weight, giving no increase in the payload weight. Designating the new reduced thrust-specific fuel consumption by (TSFC) new = (TSFC) (1 ? ? f ) and the new weight of the airplane increased by the increase in engine weight by W new ? W (1 + ? W ), where ? f and ? W are small fractional values, prove that the break even point for changes in engine weight and TSFC are given by
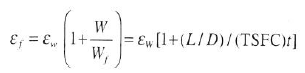
where W and W f are the average weight of the airplane during, cruise and the weight of fuel used during cruise, respectively, both before any design perturbation in engine weight or TSFC, and t is the total cruising time of flight.
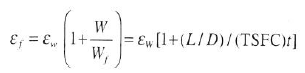
where W and W f are the average weight of the airplane during, cruise and the weight of fuel used during cruise, respectively, both before any design perturbation in engine weight or TSFC, and t is the total cruising time of flight.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
32
Consider a large four-engine jet transport with a takeoff weight of 1,350,000 lbs. By the end of the flight, 500,000 lb of fuel have been burned. Assume that the engines are now improved to obtain a 1% reduction in TSFC. Using the results of Problem 6.33, calculate the maximum allowable increase in weight of each engine for no change in take off weight.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
33
Examine Eq. (6.44) in the text. This equation is an explicit relation for V max in terms of the thrust-to-weight ratio for the airplane, and hence allows a quick analytical calculation of V max for jet-propelled airplanes. Derive an analogous relation for V max for a propeller-driven airplane in terms of the power-to-weight ratio (power loading). Note: You will find a relation that relates power loading and V max , but you will also discover that it is not possible to solve this relation explicitly for V max. Even so, this relation still allows a quicker solution for V max for propeller-driven airplanes in comparison to the numerical solution discussed in Sec. 6.6.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
34
Using your result from Prob. 6.35, calculate the maximum velocity of the CP-1 at sea level, and compare your result with the numerical solution in Sec. 6.6.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
35
Calculate analytically the maximum velocity of the CJ-1 at sea level, and compare your result with the numerical solution in Sec. 6.4.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
36
Calculate analytically the maximum rate of climb for the CP-1 at 12,000 ft and compare your result with the numerical solution in Sec. 6.10.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
37
Calculate analytically the maximum rate of climb for the CJ-1 at 24,000 ft and compare your result with the numerical solution in Sec. 6.10.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
38
The Douglas DC-3 (Fig. 6.80) has a maximum velocity of 229 mph at an altitude of 7500 ft. Each of its two engines provides a maximum of 1200 hp. Its weight is 25,000 lb. aspect ratio is 9.14, and wing area is 987 ft 2. Assume that the propeller efficiency is 0.8, and the Oswald efficiency factor is 0.7. Calculate the zero-lift drag coefficient for the DC-3.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck



