Deck 6: Principles of Stability and Control
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/9
Play
Full screen (f)
Deck 6: Principles of Stability and Control
1
For a given wing-body combination, the aerodynamic center lies 0.03 chord length ahead of the center of gravity. The moment coefficient about the center of gravity is 0.0050, and the lift coefficient is 0.50. Calculate the moment coefficient about the aerodynamic center.
The expression for the moment coefficient about the center of gravity is expresses as follows,
 Here,
Here,
 and
and
 are the moment coefficient about the center of gravity and about the aerodynamic center respectively,
are the moment coefficient about the center of gravity and about the aerodynamic center respectively,
 ,
,
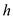 and
and
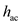 are the lift coefficient, coordinates of the center of gravity in fractions of chord length and distance of aerodynamic center from the leading edge.
are the lift coefficient, coordinates of the center of gravity in fractions of chord length and distance of aerodynamic center from the leading edge.
Rearrange the above expression of
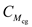 in terms of
in terms of
 is as follows,
is as follows,
 The aerodynamic center lies
The aerodynamic center lies
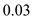 chord length ahead of the center of gravity. Thus, the value of
chord length ahead of the center of gravity. Thus, the value of
 is expresses as,
is expresses as,
 Now, the moment coefficient about the aerodynamic center is calculated as follows:
Now, the moment coefficient about the aerodynamic center is calculated as follows:
Substitute
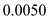 for
for
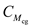 ,
,
 for
for
 and
and
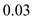 for
for
 in the above rearranged expression of
in the above rearranged expression of
 and solve,
and solve,
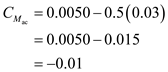 Therefore, the moment coefficient about the aerodynamic center is
Therefore, the moment coefficient about the aerodynamic center is
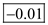 .
.
 Here,
Here,  and
and  are the moment coefficient about the center of gravity and about the aerodynamic center respectively,
are the moment coefficient about the center of gravity and about the aerodynamic center respectively,  ,
, 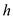 and
and 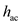 are the lift coefficient, coordinates of the center of gravity in fractions of chord length and distance of aerodynamic center from the leading edge.
are the lift coefficient, coordinates of the center of gravity in fractions of chord length and distance of aerodynamic center from the leading edge.Rearrange the above expression of
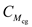 in terms of
in terms of  is as follows,
is as follows, The aerodynamic center lies
The aerodynamic center lies 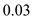 chord length ahead of the center of gravity. Thus, the value of
chord length ahead of the center of gravity. Thus, the value of  is expresses as,
is expresses as, Now, the moment coefficient about the aerodynamic center is calculated as follows:
Now, the moment coefficient about the aerodynamic center is calculated as follows:Substitute
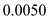 for
for 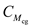 ,
,  for
for  and
and 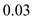 for
for  in the above rearranged expression of
in the above rearranged expression of  and solve,
and solve,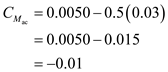 Therefore, the moment coefficient about the aerodynamic center is
Therefore, the moment coefficient about the aerodynamic center is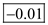 .
. 2
Consider a model of a wing-body shape mounted in a wind tunnel. The flow conditions in the test section are standard sea-level properties with a velocity of 100 m/s. The wing area and chord are 1.5 m 2 and 0.45 m, respectively. Using the wind tunnel force and moment-measuring balance, the moment about the center of gravity when the lift is zero is found to be ?12.4 N · m. When the model is pitched to another angle of attack, the lift and moment about the center of gravity are measured to be 3675 N and 20.67 N · m, respectively. Calculate the value of the moment coefficient about the aerodynamic center and the location of the aerodynamic center.
The free-stream dynamic pressure is,
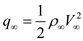 Here,
Here,
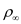 is the wind density and
is the wind density and
 is the free- stream velocity.
is the free- stream velocity.
Substitute
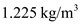 for
for
 and
and
 for
for
 .
.
 The moment of coefficient about the center of gravity is,
The moment of coefficient about the center of gravity is,
 Here,
Here,
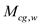 is the moment about the center of gravity,
is the moment about the center of gravity,
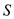 is the wing area, and
is the wing area, and
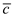 is the chord.
is the chord.
Substitute
 for
for
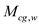 ,
,
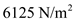 for
for
 , and
, and
 for
for
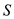 , and
, and
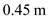 for
for
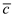 .
.
 For zero lift, the moment of coefficient about the center of gravity is equal to the moment of coefficient about the aerodynamic center.
For zero lift, the moment of coefficient about the center of gravity is equal to the moment of coefficient about the aerodynamic center.
 Substitute
Substitute
 for
for
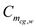 .
.
 Therefore, the value of the moment of coefficient about the aerodynamic center is
Therefore, the value of the moment of coefficient about the aerodynamic center is
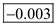 .
.
The tail-lift coefficient is,
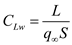 Here,
Here,
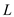 is the lift.
is the lift.
Substitute
 for
for
 ,
,
 for
for
 , and
, and
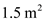 for
for
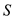 .
.


 The moment of coefficient about the center of gravity when lift is not equal to zero is,
The moment of coefficient about the center of gravity when lift is not equal to zero is,
 Substitute
Substitute
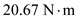 for
for
 ,
,
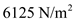 for
for
 , and
, and
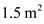 for
for
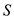 , and
, and
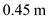 for
for
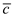 .
.
 The moment of coefficient about the center of gravity in terms of lift coefficient and moment coefficient about the aerodynamic center for the wing-body combination is,
The moment of coefficient about the center of gravity in terms of lift coefficient and moment coefficient about the aerodynamic center for the wing-body combination is,
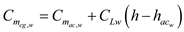 Here,
Here,
 is the location of the aerodynamic center for the chord length ahead of the center of gravity.
is the location of the aerodynamic center for the chord length ahead of the center of gravity.
Rearrange the equation for
 .
.
 Substitute
Substitute
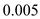 for
for

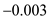 for
for
 , and
, and
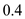 for
for
 .
.
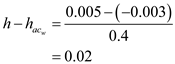 Therefore, the location of the aerodynamic center is
Therefore, the location of the aerodynamic center is
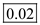 of the chord length ahead of the center of gravity.
of the chord length ahead of the center of gravity.
 Here,
Here, 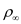 is the wind density and
is the wind density and  is the free- stream velocity.
is the free- stream velocity.Substitute
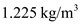 for
for and
and  for
for .
. The moment of coefficient about the center of gravity is,
The moment of coefficient about the center of gravity is, Here,
Here, 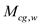 is the moment about the center of gravity,
is the moment about the center of gravity, 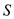 is the wing area, and
is the wing area, and 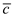 is the chord.
is the chord.Substitute
 for
for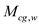 ,
, 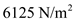 for
for , and
, and  for
for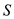 , and
, and 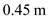 for
for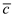 .
. For zero lift, the moment of coefficient about the center of gravity is equal to the moment of coefficient about the aerodynamic center.
For zero lift, the moment of coefficient about the center of gravity is equal to the moment of coefficient about the aerodynamic center. Substitute
Substitute for
for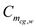 .
.  Therefore, the value of the moment of coefficient about the aerodynamic center is
Therefore, the value of the moment of coefficient about the aerodynamic center is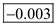 .
.The tail-lift coefficient is,
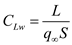 Here,
Here, 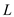 is the lift.
is the lift.Substitute
 for
for ,
,  for
for , and
, and 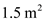 for
for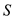 .
. 

 The moment of coefficient about the center of gravity when lift is not equal to zero is,
The moment of coefficient about the center of gravity when lift is not equal to zero is, Substitute
Substitute 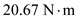 for
for ,
, 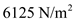 for
for , and
, and 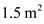 for
for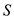 , and
, and 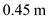 for
for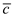 .
. The moment of coefficient about the center of gravity in terms of lift coefficient and moment coefficient about the aerodynamic center for the wing-body combination is,
The moment of coefficient about the center of gravity in terms of lift coefficient and moment coefficient about the aerodynamic center for the wing-body combination is,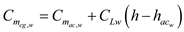 Here,
Here,  is the location of the aerodynamic center for the chord length ahead of the center of gravity.
is the location of the aerodynamic center for the chord length ahead of the center of gravity.Rearrange the equation for
 .
. Substitute
Substitute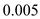 for
for
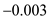 for
for , and
, and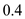 for
for .
. 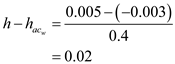 Therefore, the location of the aerodynamic center is
Therefore, the location of the aerodynamic center is 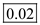 of the chord length ahead of the center of gravity.
of the chord length ahead of the center of gravity. 3
Consider the model in Prob. 7.2. If a mass of lead is added to the rear of the model so that the center of gravity is shifted rearward by a length equal to 20 percent of the chord, calculate the moment about the center of gravity when the lift is 4000 N.
7.3 From the results of Problem 7.2,
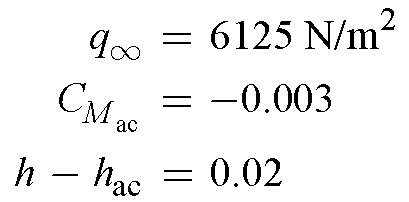 In the present problem, the e.g. has been shifted 0.2c rearward. Hence,
In the present problem, the e.g. has been shifted 0.2c rearward. Hence,
h - h ac = 0.02 + 0.2 = 0.22
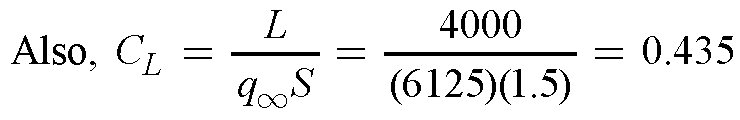
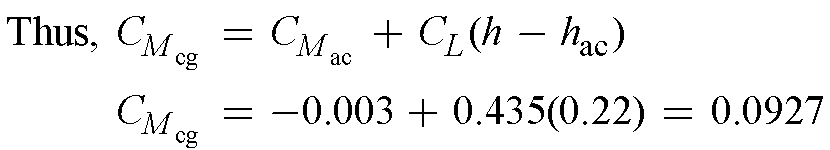
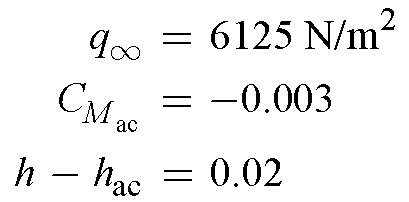 In the present problem, the e.g. has been shifted 0.2c rearward. Hence,
In the present problem, the e.g. has been shifted 0.2c rearward. Hence,h - h ac = 0.02 + 0.2 = 0.22
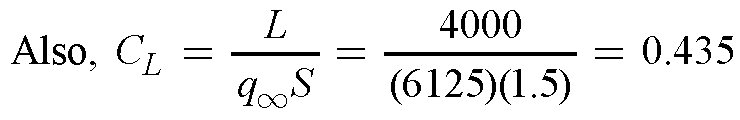
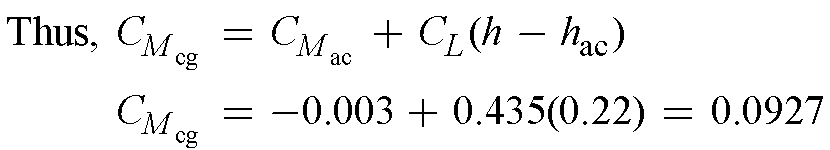
4
Consider the wing-body model in Prob. 7.2. Assume that a horizontal tail with no elevator is added to this model. The distance from the airplane's center of gravity to the tail's aerodynamic center is 1.0 m. The area of the tail is 0.4 m 2 , and the tail-setting angle is 2.0°. The lift slope of the tail is 0.12 per degree. From experimental measurement, ? 0 and ?? / ??= 0.42. If the absolute angle of attack of the model is 5º and the lift at this angle of attack is 4134 N, calculate the moment about the center of gravity.

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the wing-body-tail model of Prob. 7.4. Does this model have longitudinal static stability and balance?

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
6
For the configuration of Prob. 7.4, calculate the neutral point and static margin if h = 0.26.

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
7
Assume that an elevator is added to the horizontal tail of the configuration given in Prob. 7.4. The elevator control effectiveness is 0.04. Calculate the elevator deflection angle necessary to trim the configuration at an angle of attack of 8°.

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the configuration of Prob. 7.7. The elevator hinge moment derivatives are
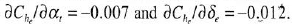 Assess the stick-free static stability of this configuration.
Assess the stick-free static stability of this configuration.
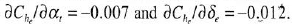 Assess the stick-free static stability of this configuration.
Assess the stick-free static stability of this configuration.
Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the canard configuration as illustrated in Fig. 7.17 b and represented by the XB-70 shown in Fig. 7.18. You will sometimes encounter a statement, either written or verbal, that the canard configuration is inherently statically unstable. This is absolutely not true. Prove that the canard configuration can be made statically stable. What design condition must hold to ensure its stability?

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck



