Deck 9: Hypersonic Vehicles
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/5
Play
Full screen (f)
Deck 9: Hypersonic Vehicles
1
Consider a laminar boundary layer on a flat plate. At the trailing edge of the plate, with a free-stream Mach number of 2, the boundary layer thickness is 0.3 in. Assuming that the Reynolds number is held constant, calculate the boundary layer thickness for a Mach number of 20.
The relation between laminar boundary layer thickness
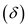 and Mach number for a compressible flow is expressed as,
and Mach number for a compressible flow is expressed as,
 …… (1)
…… (1)
Here,
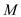 is the Mach number of the flow, and
is the Mach number of the flow, and
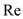 is the Reynold's of the flow.
is the Reynold's of the flow.
For Mach number equivalent to
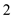 , solve for Reynolds number from equation (1) as follows,
, solve for Reynolds number from equation (1) as follows,
 And,
And,
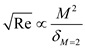 …… (2)
…… (2)
Similarly, for Mach number equivalent to
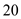 , solve for Reynolds number from equation (1) as follows,
, solve for Reynolds number from equation (1) as follows,
 …… (3)
…… (3)
Compare equation (2) and (3) and solve for boundary layer thickness
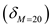 at Mach number
at Mach number
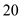 as,
as,
 …… (4)
…… (4)
Substitute
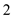 for
for
 on the left part of the equation (4) and
on the left part of the equation (4) and
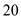 for
for
 on the right part of the equation (4),
on the right part of the equation (4),
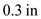 for
for
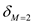 and solve,
and solve,
 Hence, the boundary layer thickness for Mach number of 20 is
Hence, the boundary layer thickness for Mach number of 20 is
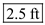 .
.
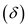 and Mach number for a compressible flow is expressed as,
and Mach number for a compressible flow is expressed as, …… (1)
…… (1)Here,
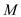 is the Mach number of the flow, and
is the Mach number of the flow, and 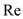 is the Reynold's of the flow.
is the Reynold's of the flow.For Mach number equivalent to
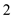 , solve for Reynolds number from equation (1) as follows,
, solve for Reynolds number from equation (1) as follows, And,
And,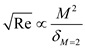 …… (2)
…… (2)Similarly, for Mach number equivalent to
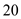 , solve for Reynolds number from equation (1) as follows,
, solve for Reynolds number from equation (1) as follows, …… (3)
…… (3)Compare equation (2) and (3) and solve for boundary layer thickness
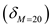 at Mach number
at Mach number 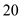 as,
as, …… (4)
…… (4)Substitute
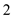 for
for 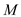 on the left part of the equation (4) and
on the left part of the equation (4) and 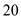 for
for  on the right part of the equation (4),
on the right part of the equation (4), 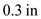 for
for 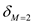 and solve,
and solve, Hence, the boundary layer thickness for Mach number of 20 is
Hence, the boundary layer thickness for Mach number of 20 is 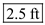 .
. 2
Consider a hypersonic vehicle flying at Mach 20 at a standard altitude of 59 km. Calculate the air temperature at a stagnation point on this vehicle. Comment on the accuracy of your answer.
The relation between temperature ratio and Mach number for a subsonic compressible flow is expressed as,
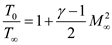 …… (1)
…… (1)
Here
 is the temperature at the stagnation point,
is the temperature at the stagnation point,
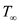 is the temperature of the free-stream flow,
is the temperature of the free-stream flow,
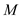 is the Mach number of the flow,
is the Mach number of the flow,
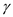 is specific heat ratio, equivalent to
is specific heat ratio, equivalent to
 ;
;
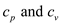 being specific heat at constant pressure and constant volume, respectively.
being specific heat at constant pressure and constant volume, respectively.
At a standard altitude of
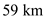 , consider the temperature
, consider the temperature
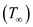 of the free-stream as,
of the free-stream as,
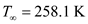 Consider the specific heat ratio
Consider the specific heat ratio
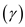 for air equivalent to
for air equivalent to
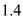 .
.
Now, calculate the temperature
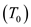 at the stagnation point from equation (1) as,
at the stagnation point from equation (1) as,
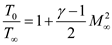 Substitute
Substitute
 for
for
 ,
,
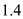 for
for
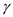 ,
,
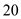 for
for
 , in the above equation and solve for
, in the above equation and solve for
 as,
as,
 Hence, the temperature at the stagnation point is
Hence, the temperature at the stagnation point is
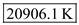 .
.
Comment:
The temperature at the stagnation point calculated above is extremely high temperature. Air becomes highly chemically reacting at such high temperatures, and the ratio of specific heats no longer remains constant; moreover, the above equation, that assumes constant
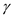 , no longer remains valid.
, no longer remains valid.
It is thus implied that hypersonic flows can be very high temperature flows. However, the gas temperature at the stagnation point will be much lower than that calculated above, as the dissociation of the air requires energy; it will be approximately
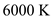 , which is still quite high, but is sufficient to cause massive dissociation of the air.
, which is still quite high, but is sufficient to cause massive dissociation of the air.
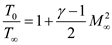 …… (1)
…… (1)Here
 is the temperature at the stagnation point,
is the temperature at the stagnation point, 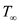 is the temperature of the free-stream flow,
is the temperature of the free-stream flow, 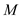 is the Mach number of the flow,
is the Mach number of the flow, 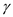 is specific heat ratio, equivalent to
is specific heat ratio, equivalent to  ;
; 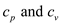 being specific heat at constant pressure and constant volume, respectively.
being specific heat at constant pressure and constant volume, respectively.At a standard altitude of
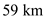 , consider the temperature
, consider the temperature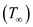 of the free-stream as,
of the free-stream as,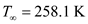 Consider the specific heat ratio
Consider the specific heat ratio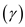 for air equivalent to
for air equivalent to 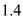 .
.Now, calculate the temperature
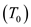 at the stagnation point from equation (1) as,
at the stagnation point from equation (1) as,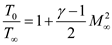 Substitute
Substitute 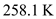 for
for 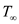 ,
, 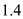 for
for 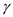 ,
, 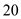 for
for  , in the above equation and solve for
, in the above equation and solve for  as,
as, Hence, the temperature at the stagnation point is
Hence, the temperature at the stagnation point is 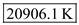 .
.Comment:
The temperature at the stagnation point calculated above is extremely high temperature. Air becomes highly chemically reacting at such high temperatures, and the ratio of specific heats no longer remains constant; moreover, the above equation, that assumes constant
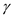 , no longer remains valid.
, no longer remains valid.It is thus implied that hypersonic flows can be very high temperature flows. However, the gas temperature at the stagnation point will be much lower than that calculated above, as the dissociation of the air requires energy; it will be approximately
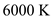 , which is still quite high, but is sufficient to cause massive dissociation of the air.
, which is still quite high, but is sufficient to cause massive dissociation of the air. 3
Assume that the nose of the Space Shuttle is spherical, with a nose radius of 1 ft. At Mach 18. calculate ( a ) the pressure coefficient at the stagnation point and ( b ) the pressure coefficient at a distance of 6 in away from the stagnation point measured along the surface.
Rayleigh Pitot tube formula is expressed as,
 …… (1)
…… (1)
Here
 is the total pressure behind the shock wave,
is the total pressure behind the shock wave,
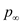 is the pressure of the free-stream,
is the pressure of the free-stream,
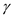 is the specific heat ratio,
is the specific heat ratio,
 is the Mach number of the free-stream.
is the Mach number of the free-stream.
Pressure coefficient
 at stagnation point is expressed as,
at stagnation point is expressed as,
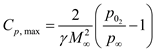 …… (2)
…… (2)
Here
 is the total pressure behind the shock wave,
is the total pressure behind the shock wave,
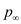 is the pressure of the free-stream,
is the pressure of the free-stream,
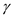 is the specific heat ratio,
is the specific heat ratio,
 is the Mach number of the free-stream.
is the Mach number of the free-stream.
Modified Newtonian law is expressed as,
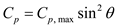 …… (3)
…… (3)
Here
 is the pressure coefficient at stagnation point,
is the pressure coefficient at stagnation point,
 is the pressure coefficient, and
is the pressure coefficient, and
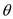 is the free-stream direction.
is the free-stream direction.
Diagram representing the flow over a sphere.
 Since,
Since,
 Thus, angle
Thus, angle
 is expressed in radians as,
is expressed in radians as,
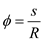 In the above diagram, angle
In the above diagram, angle
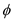 is calculated in degrees
is calculated in degrees
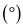 as,
as,
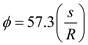 …… (4)
…… (4)
Here
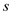 is the distance, and
is the distance, and
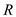 is the radius of the sphere.
is the radius of the sphere.
Now, calculate the angle
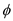 as,
as,
Substitute
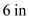 for
for
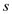 , and
, and
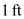 for
for
 in equation (4) and solve,
in equation (4) and solve,
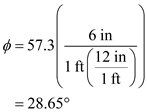 Now angle
Now angle
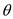 is calculated as,
is calculated as,
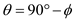 Substitute
Substitute
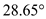 for
for
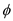 in the above equation and solve,
in the above equation and solve,
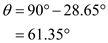 …… (5)
…… (5)
(a)
Consider the specific heat ratio
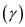 for air equivalent to
for air equivalent to
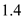 .
.
Solve for pressure ratio
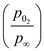 from equation (1) as,
from equation (1) as,
 Substitute
Substitute
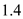 for
for
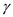 , and
, and
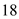 for
for
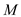 in the above equation and solve,
in the above equation and solve,
 …… (6)
…… (6)
Now calculate the magnitude of
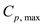 from equation (2) as,
from equation (2) as,
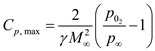 Substitute
Substitute
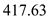 for
for
 ,
,
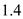 for
for
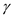 , and
, and
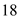 for
for
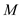 in the above equation and solve,
in the above equation and solve,
 …… (7)
…… (7)
Hence, pressure coefficient at stagnation point is
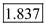 .
.
(b)
Calculate pressure coefficient
 from equation (3) as,
from equation (3) as,
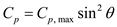 Substitute
Substitute
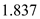 for
for
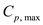 , and
, and
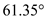 for
for
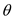 , in the above equation and solve,
, in the above equation and solve,
 Hence, pressure coefficient at a distance of
Hence, pressure coefficient at a distance of
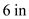 away from the stagnation point measured along the surface is
away from the stagnation point measured along the surface is
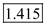 .
.
 …… (1)
…… (1)Here
 is the total pressure behind the shock wave,
is the total pressure behind the shock wave, 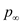 is the pressure of the free-stream,
is the pressure of the free-stream, 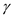 is the specific heat ratio,
is the specific heat ratio,  is the Mach number of the free-stream.
is the Mach number of the free-stream.Pressure coefficient
 at stagnation point is expressed as,
at stagnation point is expressed as,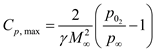 …… (2)
…… (2)Here
 is the total pressure behind the shock wave,
is the total pressure behind the shock wave, 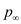 is the pressure of the free-stream,
is the pressure of the free-stream, 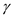 is the specific heat ratio,
is the specific heat ratio,  is the Mach number of the free-stream.
is the Mach number of the free-stream.Modified Newtonian law is expressed as,
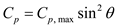 …… (3)
…… (3)Here
 is the pressure coefficient at stagnation point,
is the pressure coefficient at stagnation point,  is the pressure coefficient, and
is the pressure coefficient, and 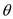 is the free-stream direction.
is the free-stream direction.Diagram representing the flow over a sphere.
 Since,
Since, 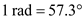 Thus, angle
Thus, angle 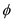 is expressed in radians as,
is expressed in radians as,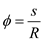 In the above diagram, angle
In the above diagram, angle 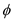 is calculated in degrees
is calculated in degrees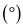 as,
as,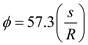 …… (4)
…… (4)Here
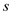 is the distance, and
is the distance, and 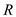 is the radius of the sphere.
is the radius of the sphere.Now, calculate the angle
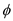 as,
as,Substitute
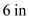 for
for 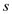 , and
, and 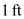 for
for  in equation (4) and solve,
in equation (4) and solve,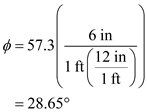 Now angle
Now angle 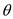 is calculated as,
is calculated as,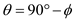 Substitute
Substitute 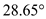 for
for 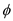 in the above equation and solve,
in the above equation and solve,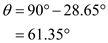 …… (5)
…… (5)(a)
Consider the specific heat ratio
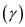 for air equivalent to
for air equivalent to 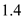 .
.Solve for pressure ratio
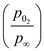 from equation (1) as,
from equation (1) as, Substitute
Substitute 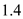 for
for 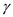 , and
, and 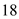 for
for 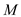 in the above equation and solve,
in the above equation and solve, …… (6)
…… (6)Now calculate the magnitude of
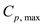 from equation (2) as,
from equation (2) as, 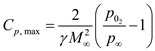 Substitute
Substitute 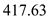 for
for  ,
, 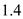 for
for 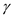 , and
, and 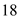 for
for 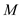 in the above equation and solve,
in the above equation and solve, …… (7)
…… (7)Hence, pressure coefficient at stagnation point is
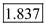 .
.(b)
Calculate pressure coefficient
 from equation (3) as,
from equation (3) as,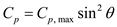 Substitute
Substitute 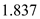 for
for 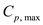 , and
, and 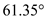 for
for 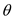 , in the above equation and solve,
, in the above equation and solve, Hence, pressure coefficient at a distance of
Hence, pressure coefficient at a distance of 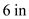 away from the stagnation point measured along the surface is
away from the stagnation point measured along the surface is 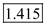 .
. 4
Consider an infinitely thin, flat plate. Using Newtonian theory, show that C L , max = 0.77 and that it occurs at ? = 54.7°.

Unlock Deck
Unlock for access to all 5 flashcards in this deck.
Unlock Deck
k this deck
5
Consider hypersonic flow over an infinitely thin, flat plate. The zero-lift drag coefficient is denoted by C D ,0. (Note that the zero-lift drag for a flat plate is entirely due to skin friction.) Consider that the wave drag coefficient is given by the Newtonian result for drag coefficient-that is, by Eq. (10.12). Also assume that the lift coefficient is given by the Newtonian result in Eq. (10.11). We wish to examine some results associated with ( L / D ) max for this flat plate. Because ( L / D ) max occurs at a small angle of attack, make the assumption of small ? in Eqs. (10.11) and (10.12). Under these conditions, show that at maximum L/D , ( a )
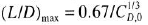 and occurs at
and occurs at
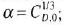 and ( b ) the wave drag coefficient = 2 C D ,0.
and ( b ) the wave drag coefficient = 2 C D ,0.
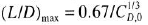 and occurs at
and occurs at 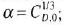 and ( b ) the wave drag coefficient = 2 C D ,0.
and ( b ) the wave drag coefficient = 2 C D ,0.
Unlock Deck
Unlock for access to all 5 flashcards in this deck.
Unlock Deck
k this deck



