Deck 11: Further Issues in Using Ols With Time Sries Data
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/28
Play
Full screen (f)
Deck 11: Further Issues in Using Ols With Time Sries Data
1
Which of the following is a strong assumption for static and finite distributed lag models?
A)Sequential exogeneity
B)Strict exogeneity
C)Dynamic completeness
D)Homoskedasticity
A)Sequential exogeneity
B)Strict exogeneity
C)Dynamic completeness
D)Homoskedasticity
C
2
If a process is said to be integrated of order one, or I(1), _____.
A)it is stationary at level
B)averages of such processes already satisfy the standard limit theorems
C)the first difference of the process is weakly dependent
D)it does not have a unit root
A)it is stationary at level
B)averages of such processes already satisfy the standard limit theorems
C)the first difference of the process is weakly dependent
D)it does not have a unit root
C
3
A stochastic process {xt: t = 1,2,….} with a finite second moment [E(xt2) < ![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_9d09_bf83_7b7fec60869d_TB8272_11.jpg) ] is covariance stationary if:
] is covariance stationary if:
A)E(xt) is variable, Var(xt) is variable, and for any t, h![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_c41a_bf83_636ba60c025e_TB8272_11.jpg) 1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
B)E(xt) is variable, Var(xt) is variable, and for any t, h![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_c41b_bf83_b76ad0b9a8ee_TB8272_11.jpg) 1, Cov(xt, xt+h) depends only on 't' and not on h.
1, Cov(xt, xt+h) depends only on 't' and not on h.
C)E(xt) is constant, Var(xt) is constant, and for any t, h![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_eb2c_bf83_3b54b8e19a47_TB8272_11.jpg) 1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
D)E(xt) is constant, Var(xt) is constant, and for any t, h![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_eb2d_bf83_1b1dcecac957_TB8272_11.jpg) 1, Cov(xt, xt+h) depends only on 't' and not on 'h'.
1, Cov(xt, xt+h) depends only on 't' and not on 'h'.
![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_9d09_bf83_7b7fec60869d_TB8272_11.jpg) ] is covariance stationary if:
] is covariance stationary if:A)E(xt) is variable, Var(xt) is variable, and for any t, h
![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_c41a_bf83_636ba60c025e_TB8272_11.jpg) 1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
1, Cov(xt, xt+h) depends only on 'h' and not on 't'.B)E(xt) is variable, Var(xt) is variable, and for any t, h
![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_c41b_bf83_b76ad0b9a8ee_TB8272_11.jpg) 1, Cov(xt, xt+h) depends only on 't' and not on h.
1, Cov(xt, xt+h) depends only on 't' and not on h.C)E(xt) is constant, Var(xt) is constant, and for any t, h
![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_eb2c_bf83_3b54b8e19a47_TB8272_11.jpg) 1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
1, Cov(xt, xt+h) depends only on 'h' and not on 't'.D)E(xt) is constant, Var(xt) is constant, and for any t, h
![<strong>A stochastic process {x<sub>t</sub>: t = 1,2,….} with a finite second moment [E(x<sub>t</sub><sup>2</sup>) < ] is covariance stationary if:</strong> A)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. B)E(x<sub>t</sub>) is variable, Var(x<sub>t</sub>) is variable, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on h. C)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 'h' and not on 't'. D)E(x<sub>t</sub>) is constant, Var(x<sub>t</sub>) is constant, and for any t, h 1, Cov(x<sub>t</sub>, x<sub>t+h</sub>) depends only on 't' and not on 'h'.](https://d2lvgg3v3hfg70.cloudfront.net/TB8272/11eb6b8a_02a7_eb2d_bf83_1b1dcecac957_TB8272_11.jpg) 1, Cov(xt, xt+h) depends only on 't' and not on 'h'.
1, Cov(xt, xt+h) depends only on 't' and not on 'h'.C
4
A process is stationary if:
A)any collection of random variables in a sequence is taken and shifted ahead by h time periods; the joint probability distribution changes.
B)any collection of random variables in a sequence is taken and shifted ahead by h time periods, the joint probability distribution remains unchanged.
C)there is serial correlation between the error terms of successive time periods and the explanatory variables and the error terms have positive covariance.
D)there is no serial correlation between the error terms of successive time periods and the explanatory variables and the error terms have positive covariance.
A)any collection of random variables in a sequence is taken and shifted ahead by h time periods; the joint probability distribution changes.
B)any collection of random variables in a sequence is taken and shifted ahead by h time periods, the joint probability distribution remains unchanged.
C)there is serial correlation between the error terms of successive time periods and the explanatory variables and the error terms have positive covariance.
D)there is no serial correlation between the error terms of successive time periods and the explanatory variables and the error terms have positive covariance.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the model: yt = 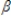 0 +
0 + 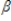 1zt1 +
1zt1 +  2zt2 + ut. Under weak dependence, the condition sufficient for consistency of OLS is:
2zt2 + ut. Under weak dependence, the condition sufficient for consistency of OLS is:
A)E(zt1|zt2) = 0.
B)E(yt |zt1, zt2) = 0.
C)E(ut |zt1, zt2) = 0.
D)E(ut |zt1, zt2) = .
.
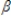 0 +
0 + 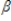 1zt1 +
1zt1 +  2zt2 + ut. Under weak dependence, the condition sufficient for consistency of OLS is:
2zt2 + ut. Under weak dependence, the condition sufficient for consistency of OLS is:A)E(zt1|zt2) = 0.
B)E(yt |zt1, zt2) = 0.
C)E(ut |zt1, zt2) = 0.
D)E(ut |zt1, zt2) =
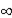 .
.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following statements is true of dynamically complete models?
A)There is scope of adding more lags to the model to better forecast the dependent variable.
B)The problem of serial correlation does not exist in dynamically complete models.
C)All econometric models are dynamically complete.
D)Sequential endogeneity is implied by dynamic completeness..
A)There is scope of adding more lags to the model to better forecast the dependent variable.
B)The problem of serial correlation does not exist in dynamically complete models.
C)All econometric models are dynamically complete.
D)Sequential endogeneity is implied by dynamic completeness..

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
7
Covariance stationarity focuses only on the first two moments of a stochastic process.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
8
In the model yt = 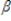 0 +
0 + 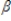 1xt1 +
1xt1 + 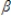 2xt2 + ….. +
2xt2 + ….. + 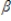 kxtk + ut, the explanatory variables, xt = (xt1, xt2 …., xtk), are sequentially exogenous if:
kxtk + ut, the explanatory variables, xt = (xt1, xt2 …., xtk), are sequentially exogenous if:
A)E(ut|xt , xt-1, ……) = E(ut) = 0, t = 1,2, ….
B)E(ut|xt , xt-1, ……)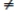 E(ut) = 0, t = 1,2, ….
E(ut) = 0, t = 1,2, ….
C)E(ut|xt , xt-1, ……) = E(ut) > 0, t = 1,2, ….
D)E(ut|xt , xt-1, ……) = E(ut) = 1, t = 1,2, ….
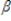 0 +
0 + 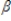 1xt1 +
1xt1 + 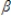 2xt2 + ….. +
2xt2 + ….. + 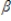 kxtk + ut, the explanatory variables, xt = (xt1, xt2 …., xtk), are sequentially exogenous if:
kxtk + ut, the explanatory variables, xt = (xt1, xt2 …., xtk), are sequentially exogenous if:A)E(ut|xt , xt-1, ……) = E(ut) = 0, t = 1,2, ….
B)E(ut|xt , xt-1, ……)
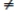 E(ut) = 0, t = 1,2, ….
E(ut) = 0, t = 1,2, ….C)E(ut|xt , xt-1, ……) = E(ut) > 0, t = 1,2, ….
D)E(ut|xt , xt-1, ……) = E(ut) = 1, t = 1,2, ….

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
9
The model yt = yt - 1 + et, t = 1, 2, … represents a:
A)AR(2) process.
B)MA(1) process.
C)random walk process.
D)random walk with a drift process.
A)AR(2) process.
B)MA(1) process.
C)random walk process.
D)random walk with a drift process.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following statements is true?
A)A model with a lagged dependent variable cannot satisfy the strict exogeneity assumption.
B)Stationarity is critical for OLS to have its standard asymptotic properties.
C)Efficient static models can be estimated for nonstationary time series.
D)In an autoregressive model, the dependent variable in the current time period varies with the error term of previous time periods.
A)A model with a lagged dependent variable cannot satisfy the strict exogeneity assumption.
B)Stationarity is critical for OLS to have its standard asymptotic properties.
C)Efficient static models can be estimated for nonstationary time series.
D)In an autoregressive model, the dependent variable in the current time period varies with the error term of previous time periods.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose ut is the error term for time period 't' in a time series regression model the explanatory variables are xt = (xt1, xt2 …., xtk). The assumption that the errors are contemporaneously homoskedastic implies that:
A)Var(ut|xt) =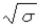 .
.
B)Var(ut|xt) = .
.
C)Var(ut|xt) = 2.
2.
D)Var(ut|xt) = .
.
A)Var(ut|xt) =
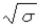 .
.B)Var(ut|xt) =
 .
.C)Var(ut|xt) =
 2.
2.D)Var(ut|xt) =
 .
.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
12
Weakly dependent processes are said to be integrated of order zero.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following statements is true?
A)A random walk process is stationary.
B)The variance of a random walk process increases as a linear function of time.
C)Adding a drift term to a random walk process makes it stationary.
D)The variance of a random walk process with a drift decreases as an exponential function of time.
A)A random walk process is stationary.
B)The variance of a random walk process increases as a linear function of time.
C)Adding a drift term to a random walk process makes it stationary.
D)The variance of a random walk process with a drift decreases as an exponential function of time.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
14
The model xt =  1xt - 1 + et, t =1,2,…. , where et is an i.i.d. sequence with zero mean and variance
1xt - 1 + et, t =1,2,…. , where et is an i.i.d. sequence with zero mean and variance  2e represents a(n):
2e represents a(n):
A)moving average process of order one.
B)moving average process of order two.
C)autoregressive process of order one.
D)autoregressive process of order two.
 1xt - 1 + et, t =1,2,…. , where et is an i.i.d. sequence with zero mean and variance
1xt - 1 + et, t =1,2,…. , where et is an i.i.d. sequence with zero mean and variance  2e represents a(n):
2e represents a(n):A)moving average process of order one.
B)moving average process of order two.
C)autoregressive process of order one.
D)autoregressive process of order two.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
15
Unit root processes, such as a random walk (with or without drift), are said to be:
A)integrated of order one.
B)integrated of order two.
C)sequentially exogenous.
D)asymptotically uncorrelated.
A)integrated of order one.
B)integrated of order two.
C)sequentially exogenous.
D)asymptotically uncorrelated.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
16
Covariance stationary sequences where Corr(xt + xt+h)  0 as
0 as 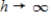 are said to be:
are said to be:
A)unit root processes.
B)trend-stationary processes.
C)serially uncorrelated.
D)asymptotically uncorrelated.
 0 as
0 as 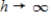 are said to be:
are said to be:A)unit root processes.
B)trend-stationary processes.
C)serially uncorrelated.
D)asymptotically uncorrelated.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
17
If ut refers to the error term at time 't' and yt - 1 refers to the dependent variable at time 't - 1', for an AR(1) process to be homoskedastic, it is required that:
A)Var(ut|yt - 1) > Var(yt|yt-1) = 2.
2.
B)Var(ut|yt - 1) = Var(yt|yt-1) > 2.
2.
C)Var(ut|yt - 1) < Var(yt|yt-1) = 2.
2.
D)Var(ut|yt - 1) = Var(yt|yt-1) = 2.
2.
A)Var(ut|yt - 1) > Var(yt|yt-1) =
 2.
2.B)Var(ut|yt - 1) = Var(yt|yt-1) >
 2.
2.C)Var(ut|yt - 1) < Var(yt|yt-1) =
 2.
2.D)Var(ut|yt - 1) = Var(yt|yt-1) =
 2.
2.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is assumed in time series regression?
A)There is no perfect collinearity between the explanatory variables.
B)The explanatory variables are contemporaneously endogenous.
C)The error terms are contemporaneously heteroskedastic.
D)The explanatory variables cannot have temporal ordering.
A)There is no perfect collinearity between the explanatory variables.
B)The explanatory variables are contemporaneously endogenous.
C)The error terms are contemporaneously heteroskedastic.
D)The explanatory variables cannot have temporal ordering.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
19
The model yt = et +  1et - 1 +
1et - 1 +  2et - 2 , t = 1, 2, ….. , where et is an i.i.d. sequence with zero mean and variance
2et - 2 , t = 1, 2, ….. , where et is an i.i.d. sequence with zero mean and variance  2e represents a(n):
2e represents a(n):
A)static model.
B)moving average process of order one.
C)moving average process of order two.
D)autoregressive process of order two.
 1et - 1 +
1et - 1 +  2et - 2 , t = 1, 2, ….. , where et is an i.i.d. sequence with zero mean and variance
2et - 2 , t = 1, 2, ….. , where et is an i.i.d. sequence with zero mean and variance  2e represents a(n):
2e represents a(n):A)static model.
B)moving average process of order one.
C)moving average process of order two.
D)autoregressive process of order two.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
20
A covariance stationary time series is weakly dependent if:
A)the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to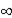 as h
as h 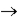 0.
0.
B)the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h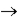
 .
.
C)the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h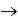
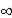 .
.
D)the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to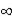 as h
as h 
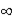 .
.
A)the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to
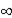 as h
as h  0.
0.B)the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h
 .
.C)the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h
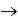
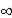 .
.D)the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to
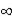 as h
as h 
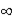 .
.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
21
The homoskedasticity assumption in time series regression suggests that the variance of the error term cannot be a function of time.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
22
If a process is a covariance stationary process, then it will have a finite second moment.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
23
Which of the following is true if yt = 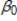 +
+ 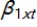 +
+  +
+  + ut is a dynamically complete model?
+ ut is a dynamically complete model?
A)E(yt| xt , yt -1, xt -1) = E(yt| xt , yt -1, xt -1,……)
B)E(yt| xt , yt -1, xt -1) = 0
C)E(yt| xt , yt -1, xt -1) = E(yt -1) + E(xt) + E(xt -1)
D)E(yt| xt , yt -1, xt -1) = E(yt)
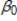 +
+ 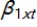 +
+  +
+  + ut is a dynamically complete model?
+ ut is a dynamically complete model?A)E(yt| xt , yt -1, xt -1) = E(yt| xt , yt -1, xt -1,……)
B)E(yt| xt , yt -1, xt -1) = 0
C)E(yt| xt , yt -1, xt -1) = E(yt -1) + E(xt) + E(xt -1)
D)E(yt| xt , yt -1, xt -1) = E(yt)

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
24
Under adaptive expectations, the expected current value of a variable does not depend on a recently observed value of the variable.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
25
The first difference of an I(1) time series is weakly dependent.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
26
The variance of a random walk process decreases as a linear function of time.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
27
If adding one more lag of the dependent variable would explain the dependent variable better, then the model is not dynamically complete.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
28
Sequential exogeneity is implied by dynamic completeness.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck



