Deck 13: The Laplace Transform
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/90
Play
Full screen (f)
Deck 13: The Laplace Transform
1
Find F ( s ) if
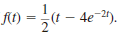
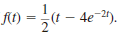
Consider the function.
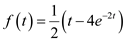 Consider the formula for Laplace transform.
Consider the formula for Laplace transform.
 Substitute
Substitute
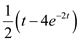 for
for
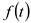 .
.


 Therefore, the Laplace transform of the function
Therefore, the Laplace transform of the function
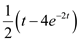 is
is
 .
.
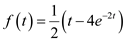 Consider the formula for Laplace transform.
Consider the formula for Laplace transform. Substitute
Substitute 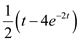 for
for 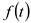 .
.

 Therefore, the Laplace transform of the function
Therefore, the Laplace transform of the function 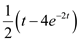 is
is  .
. 2
Find the Laplace transform of the function f ( t ) = te at sin ( t ) ( t 4).
Write the expression of the Laplace transform of
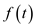 .
.
 Substitute
Substitute
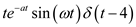 for
for
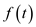 .
.
 Simplify further.
Simplify further.
 Thus, the Laplace transform of
Thus, the Laplace transform of
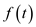 is
is
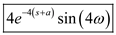 .
.
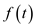 .
. Substitute
Substitute 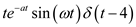 for
for 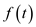 .
. Simplify further.
Simplify further. Thus, the Laplace transform of
Thus, the Laplace transform of 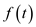 is
is 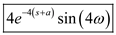 .
. 3
Given the following functions F ( s ), find the inverse Laplace transform of each function.
(a)
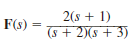
(b)
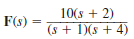
(c)
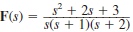
(a)
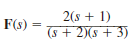
(b)
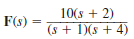
(c)
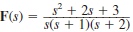
(a)
Consider the following function:
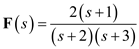 The function
The function
 is
is
 Express
Express
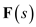 in a partial fraction expansion.
in a partial fraction expansion.
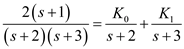 Calculate the value of
Calculate the value of
 .
.
 Calculate the value of
Calculate the value of
 .
.
 The partial fraction expansion of
The partial fraction expansion of
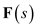 is,
is,
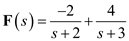 Now apply inverse Laplace transforms on both sides.
Now apply inverse Laplace transforms on both sides.
 Therefore, the function
Therefore, the function
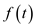 is,
is,
 (b)
(b)
Consider the following function:
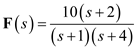 The function
The function
 is
is
 Express
Express
 in a partial fraction expansion.
in a partial fraction expansion.
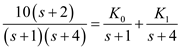 Calculate the value of
Calculate the value of
 .
.
 Calculate the value of
Calculate the value of
 .
.
 The partial fraction expansion of
The partial fraction expansion of
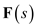 is,
is,
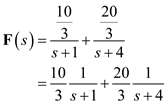 Now apply inverse Laplace transforms on both sides.
Now apply inverse Laplace transforms on both sides.
 Therefore, the function
Therefore, the function
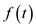 is,
is,
 (c)
(c)
Consider the following function:
 The function
The function
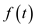 is
is
 Express
Express
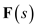 in a partial fraction expansion.
in a partial fraction expansion.
 Calculate the value of
Calculate the value of
 .
.
 Calculate the value of
Calculate the value of
 .
.
 Calculate the value of
Calculate the value of
 .
.
 The partial fraction expansion of
The partial fraction expansion of
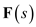 is,
is,
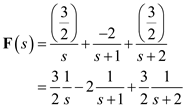 Now apply inverse Laplace transforms on both sides.
Now apply inverse Laplace transforms on both sides.
 Therefore, the function
Therefore, the function
 is,
is,

Consider the following function:
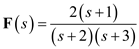 The function
The function  is
is Express
Express 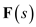 in a partial fraction expansion.
in a partial fraction expansion.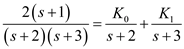 Calculate the value of
Calculate the value of  .
. Calculate the value of
Calculate the value of  .
. The partial fraction expansion of
The partial fraction expansion of 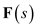 is,
is,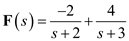 Now apply inverse Laplace transforms on both sides.
Now apply inverse Laplace transforms on both sides. Therefore, the function
Therefore, the function 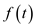 is,
is, (b)
(b)Consider the following function:
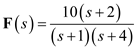 The function
The function  is
is Express
Express  in a partial fraction expansion.
in a partial fraction expansion.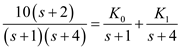 Calculate the value of
Calculate the value of  .
. Calculate the value of
Calculate the value of  .
. The partial fraction expansion of
The partial fraction expansion of 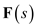 is,
is,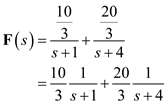 Now apply inverse Laplace transforms on both sides.
Now apply inverse Laplace transforms on both sides.  Therefore, the function
Therefore, the function 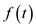 is,
is, (c)
(c)Consider the following function:
 The function
The function 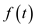 is
is Express
Express 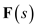 in a partial fraction expansion.
in a partial fraction expansion. Calculate the value of
Calculate the value of  .
. Calculate the value of
Calculate the value of  .
. Calculate the value of
Calculate the value of  .
. The partial fraction expansion of
The partial fraction expansion of 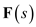 is,
is,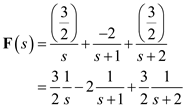 Now apply inverse Laplace transforms on both sides.
Now apply inverse Laplace transforms on both sides. Therefore, the function
Therefore, the function  is,
is,
4
Given the following functions F ( s ), find f ( t ).
(a)
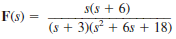
(b)
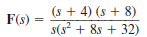
(a)
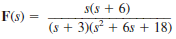
(b)
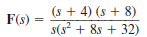

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
5
Find the inverse Laplace transform of the function F ( s ) using the convolution integral.
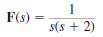
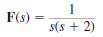

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
6
The switch in the circuit in Fig. P13.63 has been closed for a long time and is opened at t = 0. Find i ( t ) for t 0, using Laplace transforms.
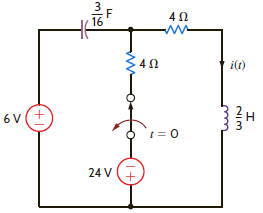
Figure P13.63

Figure P13.63

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
7
The Laplace transform function for the output voltage of a network is expressed in the following form:
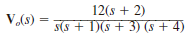
Determine the value of this voltage; that is, v o ( t ) at t
a. 6 V
b. 2 V
c. 12 V
d. 4 V
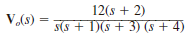
Determine the value of this voltage; that is, v o ( t ) at t
a. 6 V
b. 2 V
c. 12 V
d. 4 V

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
8
Given
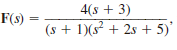 find f ( t ).
find f ( t ).
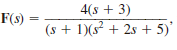 find f ( t ).
find f ( t ).
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
9
In the circuit in Fig. E3.18, the switch opens at t = 0. Use Laplace transforms to find v o ( t ) for t 0.
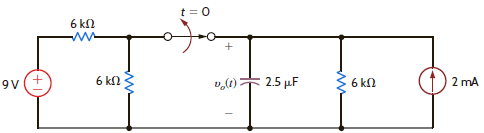
Figure E3.18

Figure E3.18

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
10
Given the following functions F ( s ), find f ( t ).
(a)
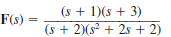
(b)
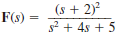
(a)
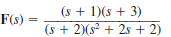
(b)
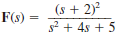

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
11
Find f ( t ) using the convolution integral if
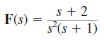
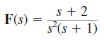

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
12
The switch in the circuit in Fig. P13.64 has been closed for a long time and is opened at t = 0. Find i ( t ) for t 0 using Laplace transforms.
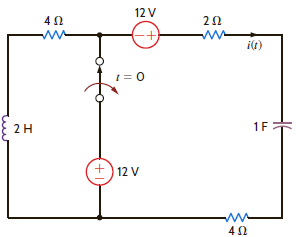
Figure P13.64

Figure P13.64

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
13
Use the time-shifting theorem to determine [ f ( t )], where f ( t ) = [e ( t 2) e 2( t 2) ] u ( t 2).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
14
Find F ( s ) if f ( t ) = e at sin t u(t 1).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
15
Given the following functions F ( s ), find f ( t ).
(a)
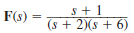
(b)
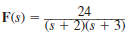
(c)

(d)
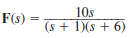
(a)
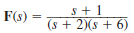
(b)
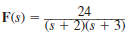
(c)

(d)
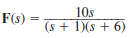

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
16
Given the following functions F ( s ), find f ( t ).
(a)
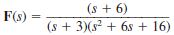
(b)

(a)
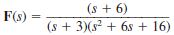
(b)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
17
Find f ( t ) using convolution if F ( s ) is
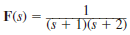
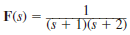

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
18
The switch in the circuit in Fig. P13.65 has been closed for a long time and is opened at t = 0. Find i ( t ) for t 0 using Laplace transforms.
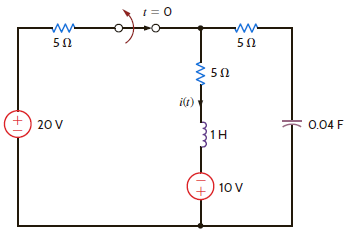
Figure P13.65

Figure P13.65

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
19
If f ( t ) = te ( t 1) u ( t 1) e ( t 1) u ( t 1), determine F ( s ) using the time-shifting theorem.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
20
Determine f ( t ) if F ( s ) = s /( s + 1) 2.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
21
In the circuit in Fig. E3.19, the switch opens at t = 0. Use Laplace transforms to find i ( t ) for t 0.

Figure E3.19

Figure E3.19

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
22
Given the following functions F ( s ), find f ( t ).
(a)
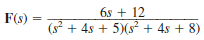
(b)

(a)
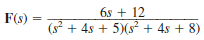
(b)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
23
Find f ( t ) using convolution if F ( s ) is
(a)
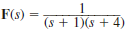
(b)
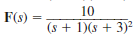
(a)
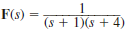
(b)
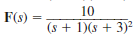

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
24
In the circuit shown in Fig. P13.66, switch action occurs at t = 0. Determine the voltage u 0 (t), t 0 using Laplace transforms.
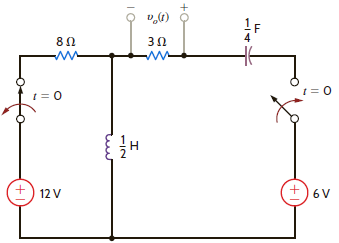
Figure P13.66

Figure P13.66

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
25
The output of a network is expressed as
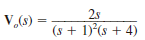
Determine the output as a function of time.
a.
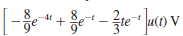
b.
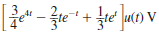
c.
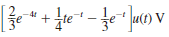
d.

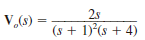
Determine the output as a function of time.
a.
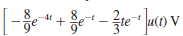
b.
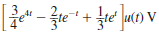
c.
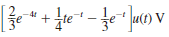
d.


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
26
Find F ( s ) if f ( t ) = te at u ( t 4).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
27
Given the following functions F ( s ), find f ( t ).
(a)
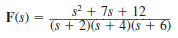
(b)
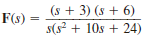
(c)
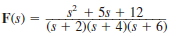
(d)
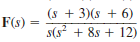
(a)
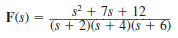
(b)
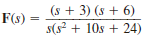
(c)
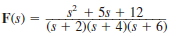
(d)
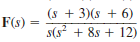

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
28
Find the inverse Laplace transform of the following functions.
(a)
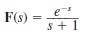
(b)
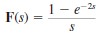
(c)
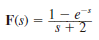
(a)
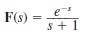
(b)
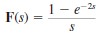
(c)
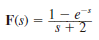

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
29
Find the initial and final values of f ( t ) if F ( s ) is given as
(a)
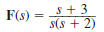
(b)
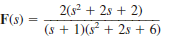
(c)

(a)
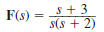
(b)
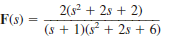
(c)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
30
Use property number 7 to find [ f ( t )] if f ( t ) = t e at u ( t 1).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
31
If F ( s ) = ( s + 2)/ s 2 ( s + 1), find f ( t ).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
32
Given the following functions F ( s ), find f ( t ).
(a)
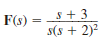
(b)
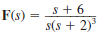
(a)
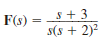
(b)
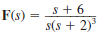

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
33
Find f ( t ) if F ( s ) is given by the following functions:
(a)
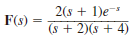
(b)
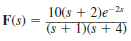
(c)

(a)
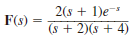
(b)
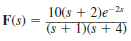
(c)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
34
Determine the initial and final values of f ( t ) if F ( s ) is given by the expressions
(a)
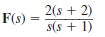
(b)
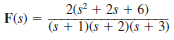
(c)
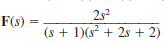
(a)
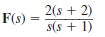
(b)
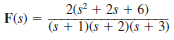
(c)
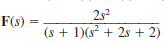

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
35
Find F ( s ) if f ( t ) = e 4 t ( t e t ).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
36
Use the results of property 3 and the fact that if f ( t ) = e t sin t , then F ( s ) = 1/( s + 1) 2 + 1 to find the Laplace transform of f ( t ) = e 2 t sin 2 t.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
37
Given the following functions F ( s ), find the inverse Laplace transform of each function.
(a)
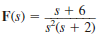
(b)
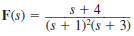
(a)
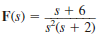
(b)
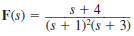

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
38
Find the inverse Laplace transform of the following functions.
(a)
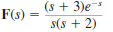
(b)
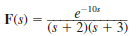
(c)
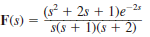
(d)
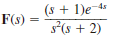
(a)
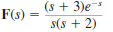
(b)
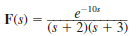
(c)
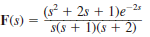
(d)
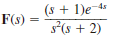

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
39
Find the final values of the time function f ( t ) given that
(a)
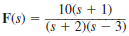
(b)
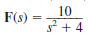
(a)
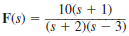
(b)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the following differential equation using Laplace transforms:
![Solve the following differential equation using Laplace transforms: a. [ 2 e 2 t + e 4 t 3e 3t ] u ( t ) b. [ 3 e 2t + e 4 t + e 3 t ] u ( t ) c. [ e 2t + e 4 t 2 e 3 t ] u ( t ) d. [ 4 e 2t e 4 2 e 3 t ] u ( t )](https://d2lvgg3v3hfg70.cloudfront.net/SM4993/11eb71f4_a2f5_5ce8_b53a_bbece4931638_SM4993_00.jpg)
a. [ 2 e 2 t + e 4 t 3e 3t ] u ( t )
b. [ 3 e 2t + e 4 t + e 3 t ] u ( t )
c. [ e 2t + e 4 t 2 e 3 t ] u ( t )
d. [ 4 e 2t e 4 2 e 3 t ] u ( t )
![Solve the following differential equation using Laplace transforms: a. [ 2 e 2 t + e 4 t 3e 3t ] u ( t ) b. [ 3 e 2t + e 4 t + e 3 t ] u ( t ) c. [ e 2t + e 4 t 2 e 3 t ] u ( t ) d. [ 4 e 2t e 4 2 e 3 t ] u ( t )](https://d2lvgg3v3hfg70.cloudfront.net/SM4993/11eb71f4_a2f5_5ce8_b53a_bbece4931638_SM4993_00.jpg)
a. [ 2 e 2 t + e 4 t 3e 3t ] u ( t )
b. [ 3 e 2t + e 4 t + e 3 t ] u ( t )
c. [ e 2t + e 4 t 2 e 3 t ] u ( t )
d. [ 4 e 2t e 4 2 e 3 t ] u ( t )

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
41
Given
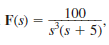 find f ( t ).
find f ( t ).
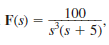 find f ( t ).
find f ( t ).
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
42
Given the following functions F ( s ), find f ( t ).
(a)
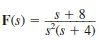
(b)
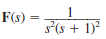
(a)
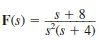
(b)
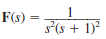

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
43
Find f ( t ) if F ( s ) is given by the following function:
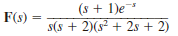 .
.
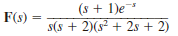 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
44
Find the final values of the time function f ( t ) given that
(a)
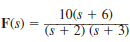
(b)
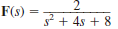
(a)
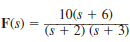
(b)
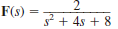

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
45
Use property number 5 to find [ f ( t )] if f ( t ) = e at u ( t 1).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
46
Find [ f ( t )] if f ( t ) = t 2 e at ( t 2).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
47
Find f ( t ) if F ( s ) is given by the expression.
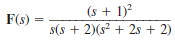 .
.
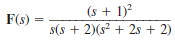 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
48
Find the inverse Laplace transform of the function
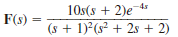 .
.
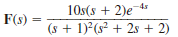 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
49
Find the initial and final values of the time function f ( t ) if F ( s ) is given as
(a)
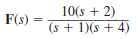
(b)
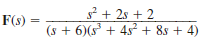
(c)
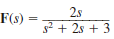
(a)
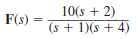
(b)
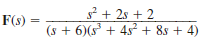
(c)
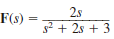

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
50
Find f ( t ) if F ( s ) = 10( s + 6)/ s ( s + 1)( s + 3).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
51
Find the initial and final values of the function f ( t ) if F ( s ) = is given by the expression
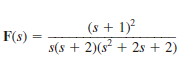
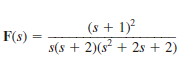

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
52
Find the inverse Laplace transform of F ( s ) where
 .
.
 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
53
Find f ( t ) if F ( s ) is given by the expression
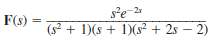 .
.
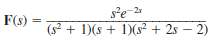 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
54
Find the initial and final values of f ( t ) if F ( s ) is given as
(a)
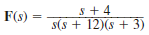
(b)
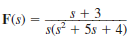
(c)

(a)
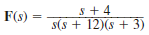
(b)
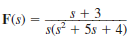
(c)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
55
If f ( t ) = e at , show that F ( s ) = 1/( s + a ).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
56
Find the Laplace transform of the function f ( t ) = e at ( t 1).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
57
If f ( t ) = t sin ( t ) u ( t 1), find F ( s ).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
58
Find the inverse Laplace transform of the function
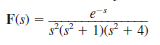 .
.
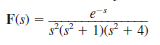 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
59
Use Laplace transforms to solve the following differential equations.
(a)
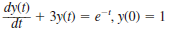
(b)
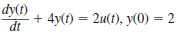
(a)
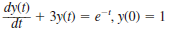
(b)
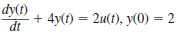

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
60
In the network in Fig. P13.57, the switch opens at t = 0. Use Laplace transforms to find v o ( t ) for t 0.
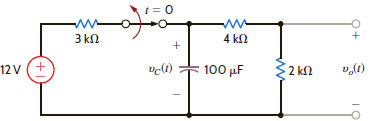
Figure P13.57

Figure P13.57

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
61
The output function of a network is expressed using Laplace transforms in the following form:
![The output function of a network is expressed using Laplace transforms in the following form: Find the output v o ( t ) as a function of time. a. [ 12 + 3 e 2 t + 4 e t ] u ( t ) V b. [ 2 + 4 e 2 t + 8 e t ] u ( t )V c. [ 6 + 6 e 2 t 12 e t ] u ( t ) V d. [ 3 + 2 e 2 t 6 e t ] u ( t )V](https://d2lvgg3v3hfg70.cloudfront.net/SM4993/11eb71f4_a2e0_eb12_b53a_73ca784f7a48_SM4993_00.jpg)
Find the output v o ( t ) as a function of time.
a. [ 12 + 3 e 2 t + 4 e t ] u ( t ) V
b. [ 2 + 4 e 2 t + 8 e t ] u ( t )V
c. [ 6 + 6 e 2 t 12 e t ] u ( t ) V
d. [ 3 + 2 e 2 t 6 e t ] u ( t )V
![The output function of a network is expressed using Laplace transforms in the following form: Find the output v o ( t ) as a function of time. a. [ 12 + 3 e 2 t + 4 e t ] u ( t ) V b. [ 2 + 4 e 2 t + 8 e t ] u ( t )V c. [ 6 + 6 e 2 t 12 e t ] u ( t ) V d. [ 3 + 2 e 2 t 6 e t ] u ( t )V](https://d2lvgg3v3hfg70.cloudfront.net/SM4993/11eb71f4_a2e0_eb12_b53a_73ca784f7a48_SM4993_00.jpg)
Find the output v o ( t ) as a function of time.
a. [ 12 + 3 e 2 t + 4 e t ] u ( t ) V
b. [ 2 + 4 e 2 t + 8 e t ] u ( t )V
c. [ 6 + 6 e 2 t 12 e t ] u ( t ) V
d. [ 3 + 2 e 2 t 6 e t ] u ( t )V

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
62
If F ( s ) = 12( s + 2)/ s ( s + 1), find f ( t ).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
63
Find the initial and final values of the time function f ( t ) if
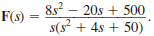
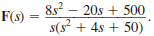

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
64
Given the following functions F ( s ), find f ( t ).
(a)
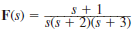
(b)
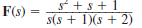
(a)
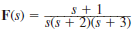
(b)
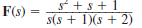

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the following integrodifferential equation using Laplace transforms.
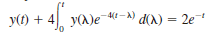 t 0
t 0
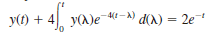 t 0
t 0
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
66
In the circuit in Fig. P13.58, the switch moves from position 1 to position 2 at t = 0. Use Laplace transforms to find v ( t ) for t 0.

Figure P13.58

Figure P13.58

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
67
Use the time-shifting theorem to determine [ f ( t )] where f ( t )=[ t 1 + e ( t 1) ] u ( t 1).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
68
If f ( t ) = e at sin t, show that
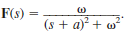
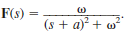

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
69
If F ( s ) = ( s + 1) 2 ( s + 3) 2 /( s + 2)( s + 4), find f ( t ).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
70
Given the following functions F ( s ), find f ( t ).
(a)
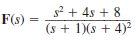
(b)
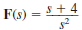
(a)
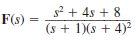
(b)
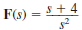

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the following integrodifferential equation using Laplace transforms.
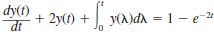 , y(0) = 0, t 0
, y(0) = 0, t 0
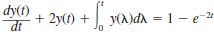 , y(0) = 0, t 0
, y(0) = 0, t 0
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
72
In the network in Fig. P13.59, the switch opens at t = 0. Use Laplace transforms to find i ( t) for t 0.
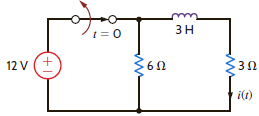
Figure P13.59

Figure P13.59

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
73
If f ( t ) = sin t, show that F ( s ) = /( s 2 + 2 ).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
74
Given
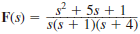 , find f ( t ).
, find f ( t ).
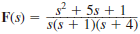 , find f ( t ).
, find f ( t ).
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
75
Use the Laplace transform to find y ( t ) if



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
76
Given the following functions F ( s ), find f ( t ).
(a)
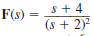
(b)
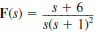
(a)
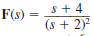
(b)
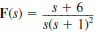

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the following differential equations using Laplace transforms.
(a)

(b)
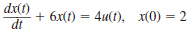
(a)

(b)
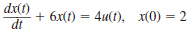

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
78
In the network in Fig. P13.60, the switch opens at t = 0. Use Laplace transforms to find i ( t ) for t 0.
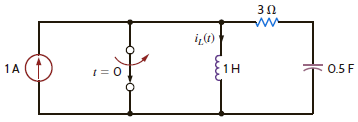
Figure P13.60

Figure P13.60

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
79
The Laplace transform function representing the output voltage of a network is expressed as

Determine the value of v o ( t ) at t = 100 ms.
a. 0.64 V
b. 0.45 V
c. 0.33 V
d. 0.24 V

Determine the value of v o ( t ) at t = 100 ms.
a. 0.64 V
b. 0.45 V
c. 0.33 V
d. 0.24 V

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
80
If f(t) = e at , show that F ( s ) =
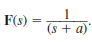
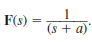

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck



