Deck 16: Capital and Time
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/12
Play
Full screen (f)
Deck 16: Capital and Time
1
An individual has a fixed wealth (W) to allocate between consumption in two periods ( c 1 and c 2 ). The individual's utility function is given by
 and the budget constraint is
and the budget constraint is

where r is the one-period interest rate.
a. Show that, in order to maximize utility given this budget constraint, the individual should choose c 1 and c 2 such that the MRS (of c 1 for c 2 ) is equal to 1 + r.
b. Show that
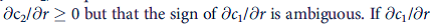 is negative, what can you conclude about the price elasticity of demand for c 2 ?
is negative, what can you conclude about the price elasticity of demand for c 2 ?
c. How would your conclusions from part (b) be amended if the individual received income in each period ( y 1 and y 2 ) such that the budget constraint is given by
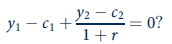
 and the budget constraint is
and the budget constraint is
where r is the one-period interest rate.
a. Show that, in order to maximize utility given this budget constraint, the individual should choose c 1 and c 2 such that the MRS (of c 1 for c 2 ) is equal to 1 + r.
b. Show that
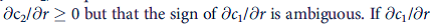 is negative, what can you conclude about the price elasticity of demand for c 2 ?
is negative, what can you conclude about the price elasticity of demand for c 2 ?c. How would your conclusions from part (b) be amended if the individual received income in each period ( y 1 and y 2 ) such that the budget constraint is given by
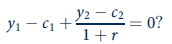
a) The utility function is
 The budget constraint is:
The budget constraint is:
 Setting the Lagrange
Setting the Lagrange
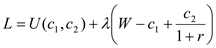 Yields the first order conditions
Yields the first order conditions
 ......(1)
......(1)
 ......(2)
......(2)
Dividing equation (1) by equation (2), we get
 Since MRS =
Since MRS =
 , hence MRS =
, hence MRS =
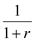 b)Consumption in period 2 is a normal good with price
b)Consumption in period 2 is a normal good with price
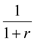 . Since the substitution effect is negative, this means and increase in
. Since the substitution effect is negative, this means and increase in
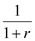 means a decrease in c 2. However, an increase in
means a decrease in c 2. However, an increase in
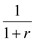 means that r must have decreased. Moreover the income effect is positive as it is a normal good. Hence there is a positive relation between c 2 and r i.e.
means that r must have decreased. Moreover the income effect is positive as it is a normal good. Hence there is a positive relation between c 2 and r i.e.
 .
.
 is ambiguous because the substitution effect predicts
is ambiguous because the substitution effect predicts
 but the income effect predicts
but the income effect predicts
 If
If
 this means that a fall in
this means that a fall in
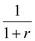 which is the price of c 2 raises total spending on c 2. Therefore, demand for c 2 is price elastic.
which is the price of c 2 raises total spending on c 2. Therefore, demand for c 2 is price elastic.
c) Old budget constraint:
 The new budget constraint is:
The new budget constraint is:
 Which can also be represented as
Which can also be represented as
 As can be seen, the new budget constraint has same slope as in part (a). It passes through
As can be seen, the new budget constraint has same slope as in part (a). It passes through
c 1 = y 1 and c 2 = y 2. If c 1 * y 1 , the individual borrows in period 1 and repays in period 2. If c 1 * y 1 individual saves in period 1 and uses savings in period 2.
 The budget constraint is:
The budget constraint is: Setting the Lagrange
Setting the Lagrange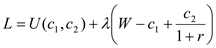 Yields the first order conditions
Yields the first order conditions ......(1)
......(1) ......(2)
......(2)Dividing equation (1) by equation (2), we get
 Since MRS =
Since MRS =  , hence MRS =
, hence MRS = 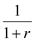 b)Consumption in period 2 is a normal good with price
b)Consumption in period 2 is a normal good with price 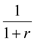 . Since the substitution effect is negative, this means and increase in
. Since the substitution effect is negative, this means and increase in 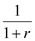 means a decrease in c 2. However, an increase in
means a decrease in c 2. However, an increase in 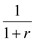 means that r must have decreased. Moreover the income effect is positive as it is a normal good. Hence there is a positive relation between c 2 and r i.e.
means that r must have decreased. Moreover the income effect is positive as it is a normal good. Hence there is a positive relation between c 2 and r i.e.  .
. is ambiguous because the substitution effect predicts
is ambiguous because the substitution effect predicts  but the income effect predicts
but the income effect predicts  If
If  this means that a fall in
this means that a fall in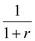 which is the price of c 2 raises total spending on c 2. Therefore, demand for c 2 is price elastic.
which is the price of c 2 raises total spending on c 2. Therefore, demand for c 2 is price elastic.c) Old budget constraint:
 The new budget constraint is:
The new budget constraint is: Which can also be represented as
Which can also be represented as As can be seen, the new budget constraint has same slope as in part (a). It passes through
As can be seen, the new budget constraint has same slope as in part (a). It passes through c 1 = y 1 and c 2 = y 2. If c 1 * y 1 , the individual borrows in period 1 and repays in period 2. If c 1 * y 1 individual saves in period 1 and uses savings in period 2.
2
Assume that an individual expects to work for 40 years and then retire with a life expectancy of an additional 20 years. Suppose also that the individual's earnings increase at a rate of 3 percent per year and that the interest rate is also 3 percent (the overall price level is constant in this problem). What (constant) fraction of income must the individual save in each working year to be able to finance a level of retirement income equal to 60 percent of earnings in the year just prior to retirement?
In this exercise we use continuous time for simplicity
As the individual's earnings increase at the rate of 3 percent per year,
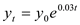 So income at the 40 th year will be given by
So income at the 40 th year will be given by
 Savings each year are given by
Savings each year are given by
 At the rate of interest of 3% per year, accumulated savings after 40 years are given by
At the rate of interest of 3% per year, accumulated savings after 40 years are given by
 At the rate of interest of 3% per year, the present value of spending in retirement (dissavings) is given by
At the rate of interest of 3% per year, the present value of spending in retirement (dissavings) is given by
 The accumulated savings should equal the present discounted value of dissavings. Hence,
The accumulated savings should equal the present discounted value of dissavings. Hence,
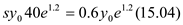 From the above condition we get the optimal amount of saving, which is equal to
From the above condition we get the optimal amount of saving, which is equal to
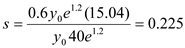 Hence, the individuals should save 22.5% of his income per year.
Hence, the individuals should save 22.5% of his income per year.
As the individual's earnings increase at the rate of 3 percent per year,
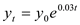 So income at the 40 th year will be given by
So income at the 40 th year will be given by Savings each year are given by
Savings each year are given by At the rate of interest of 3% per year, accumulated savings after 40 years are given by
At the rate of interest of 3% per year, accumulated savings after 40 years are given by At the rate of interest of 3% per year, the present value of spending in retirement (dissavings) is given by
At the rate of interest of 3% per year, the present value of spending in retirement (dissavings) is given by The accumulated savings should equal the present discounted value of dissavings. Hence,
The accumulated savings should equal the present discounted value of dissavings. Hence, 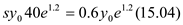 From the above condition we get the optimal amount of saving, which is equal to
From the above condition we get the optimal amount of saving, which is equal to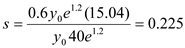 Hence, the individuals should save 22.5% of his income per year.
Hence, the individuals should save 22.5% of his income per year. 3
As scotch whiskey ages, its value increases. One dollar of scotch at year 0 is worth
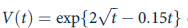 dollars at time t. If the interest rate is 5 percent, after how many years should a person sell scotch in order to maximize the PDV of this sale?
dollars at time t. If the interest rate is 5 percent, after how many years should a person sell scotch in order to maximize the PDV of this sale?
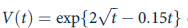 dollars at time t. If the interest rate is 5 percent, after how many years should a person sell scotch in order to maximize the PDV of this sale?
dollars at time t. If the interest rate is 5 percent, after how many years should a person sell scotch in order to maximize the PDV of this sale?The PDV is given by
PDV =
 The first order condition for the above function is given by
The first order condition for the above function is given by
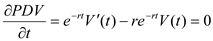 So for maximizing the present value,
So for maximizing the present value,
 So,
So,

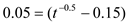 We get,
We get,
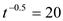 Which means that
Which means that
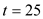
PDV =
 The first order condition for the above function is given by
The first order condition for the above function is given by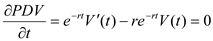 So for maximizing the present value,
So for maximizing the present value, So,
So,
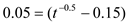 We get,
We get,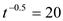 Which means that
Which means that 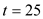
4
As in Example 17.3, suppose trees are produced by applying 1 unit of labor at time 0. The value of the wood contained in a tree is given at any time t by f (t). If the market wage rate is w and the real interest rate is r, what is the PDV of this production process, and how should t be chosen to maximize this PDV?
a. If the optimal value of t is denoted by t * , show that the ''no pure profit'' condition of perfect competition will necessitate that
![As in Example 17.3, suppose trees are produced by applying 1 unit of labor at time 0. The value of the wood contained in a tree is given at any time t by f (t). If the market wage rate is w and the real interest rate is r, what is the PDV of this production process, and how should t be chosen to maximize this PDV? a. If the optimal value of t is denoted by t * , show that the ''no pure profit'' condition of perfect competition will necessitate that Can you explain the meaning of this expression? b. A tree sold before t * will not be cut down immediately. Rather, it still will make sense for the new owner to let the tree continue to mature until t *. Show that the price of a u-year-old tree will be weru and that this price will exceed the value of the wood in the tree [ f (u)] for every value of u except u = t * (when these two values are equal). c. Suppose a landowner has a ''balanced'' woodlot with one tree of ''each'' age from 0 to t *. What is the value of this woodlot? Hint: It is the sum of the values of all trees in the lot. d. If the value of the woodlot is V, show that the instantaneous interest on V (that is, is equal to the ''profits'' earned at each instant by the landowner, where by profits we mean the difference between the revenue obtained from selling a fully matured tree [ f (t * )] and the cost of planting a new one (w). This result shows there is no pure profit in borrowing to buy a woodlot, because one would have to pay in interest at each instant exactly what would be earned from cutting a fully matured tree.](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c3_7fbc_adfc_c9d06cbdabcf_SM3017_11.jpg)
Can you explain the meaning of this expression?
b. A tree sold before t * will not be cut down immediately. Rather, it still will make sense for the new owner to let the tree continue to mature until t *. Show that the price of a u-year-old tree will be weru and that this price will exceed the value of the wood in the tree [ f (u)] for every value of u except u = t * (when these two values are equal).
c. Suppose a landowner has a ''balanced'' woodlot with one tree of ''each'' age from 0 to t *. What is the value of this woodlot? Hint: It is the sum of the values of all trees in the lot.
d. If the value of the woodlot is V, show that the instantaneous interest on V (that is,
![As in Example 17.3, suppose trees are produced by applying 1 unit of labor at time 0. The value of the wood contained in a tree is given at any time t by f (t). If the market wage rate is w and the real interest rate is r, what is the PDV of this production process, and how should t be chosen to maximize this PDV? a. If the optimal value of t is denoted by t * , show that the ''no pure profit'' condition of perfect competition will necessitate that Can you explain the meaning of this expression? b. A tree sold before t * will not be cut down immediately. Rather, it still will make sense for the new owner to let the tree continue to mature until t *. Show that the price of a u-year-old tree will be weru and that this price will exceed the value of the wood in the tree [ f (u)] for every value of u except u = t * (when these two values are equal). c. Suppose a landowner has a ''balanced'' woodlot with one tree of ''each'' age from 0 to t *. What is the value of this woodlot? Hint: It is the sum of the values of all trees in the lot. d. If the value of the woodlot is V, show that the instantaneous interest on V (that is, is equal to the ''profits'' earned at each instant by the landowner, where by profits we mean the difference between the revenue obtained from selling a fully matured tree [ f (t * )] and the cost of planting a new one (w). This result shows there is no pure profit in borrowing to buy a woodlot, because one would have to pay in interest at each instant exactly what would be earned from cutting a fully matured tree.](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c3_7fbd_adfc_2d5903314760_SM3017_11.jpg) is equal to the ''profits'' earned at each instant by the landowner, where by profits we mean the difference between the revenue obtained from selling a fully matured tree [ f (t * )] and the cost of planting a new one (w). This result shows there is no pure profit in borrowing to buy a woodlot, because one would have to pay in interest at each instant exactly what would be earned from cutting a fully matured tree.
is equal to the ''profits'' earned at each instant by the landowner, where by profits we mean the difference between the revenue obtained from selling a fully matured tree [ f (t * )] and the cost of planting a new one (w). This result shows there is no pure profit in borrowing to buy a woodlot, because one would have to pay in interest at each instant exactly what would be earned from cutting a fully matured tree.
a. If the optimal value of t is denoted by t * , show that the ''no pure profit'' condition of perfect competition will necessitate that
![As in Example 17.3, suppose trees are produced by applying 1 unit of labor at time 0. The value of the wood contained in a tree is given at any time t by f (t). If the market wage rate is w and the real interest rate is r, what is the PDV of this production process, and how should t be chosen to maximize this PDV? a. If the optimal value of t is denoted by t * , show that the ''no pure profit'' condition of perfect competition will necessitate that Can you explain the meaning of this expression? b. A tree sold before t * will not be cut down immediately. Rather, it still will make sense for the new owner to let the tree continue to mature until t *. Show that the price of a u-year-old tree will be weru and that this price will exceed the value of the wood in the tree [ f (u)] for every value of u except u = t * (when these two values are equal). c. Suppose a landowner has a ''balanced'' woodlot with one tree of ''each'' age from 0 to t *. What is the value of this woodlot? Hint: It is the sum of the values of all trees in the lot. d. If the value of the woodlot is V, show that the instantaneous interest on V (that is, is equal to the ''profits'' earned at each instant by the landowner, where by profits we mean the difference between the revenue obtained from selling a fully matured tree [ f (t * )] and the cost of planting a new one (w). This result shows there is no pure profit in borrowing to buy a woodlot, because one would have to pay in interest at each instant exactly what would be earned from cutting a fully matured tree.](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c3_7fbc_adfc_c9d06cbdabcf_SM3017_11.jpg)
Can you explain the meaning of this expression?
b. A tree sold before t * will not be cut down immediately. Rather, it still will make sense for the new owner to let the tree continue to mature until t *. Show that the price of a u-year-old tree will be weru and that this price will exceed the value of the wood in the tree [ f (u)] for every value of u except u = t * (when these two values are equal).
c. Suppose a landowner has a ''balanced'' woodlot with one tree of ''each'' age from 0 to t *. What is the value of this woodlot? Hint: It is the sum of the values of all trees in the lot.
d. If the value of the woodlot is V, show that the instantaneous interest on V (that is,
![As in Example 17.3, suppose trees are produced by applying 1 unit of labor at time 0. The value of the wood contained in a tree is given at any time t by f (t). If the market wage rate is w and the real interest rate is r, what is the PDV of this production process, and how should t be chosen to maximize this PDV? a. If the optimal value of t is denoted by t * , show that the ''no pure profit'' condition of perfect competition will necessitate that Can you explain the meaning of this expression? b. A tree sold before t * will not be cut down immediately. Rather, it still will make sense for the new owner to let the tree continue to mature until t *. Show that the price of a u-year-old tree will be weru and that this price will exceed the value of the wood in the tree [ f (u)] for every value of u except u = t * (when these two values are equal). c. Suppose a landowner has a ''balanced'' woodlot with one tree of ''each'' age from 0 to t *. What is the value of this woodlot? Hint: It is the sum of the values of all trees in the lot. d. If the value of the woodlot is V, show that the instantaneous interest on V (that is, is equal to the ''profits'' earned at each instant by the landowner, where by profits we mean the difference between the revenue obtained from selling a fully matured tree [ f (t * )] and the cost of planting a new one (w). This result shows there is no pure profit in borrowing to buy a woodlot, because one would have to pay in interest at each instant exactly what would be earned from cutting a fully matured tree.](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c3_7fbd_adfc_2d5903314760_SM3017_11.jpg) is equal to the ''profits'' earned at each instant by the landowner, where by profits we mean the difference between the revenue obtained from selling a fully matured tree [ f (t * )] and the cost of planting a new one (w). This result shows there is no pure profit in borrowing to buy a woodlot, because one would have to pay in interest at each instant exactly what would be earned from cutting a fully matured tree.
is equal to the ''profits'' earned at each instant by the landowner, where by profits we mean the difference between the revenue obtained from selling a fully matured tree [ f (t * )] and the cost of planting a new one (w). This result shows there is no pure profit in borrowing to buy a woodlot, because one would have to pay in interest at each instant exactly what would be earned from cutting a fully matured tree.
Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
5
This problem focuses on the interaction of the corporate profits tax with firms' investment decisions.
a. Suppose (contrary to fact) that profits were defined for tax purposes as what we have called pure economic profits. How would a tax on such profits affect investment decisions?
b. In fact, profits are defined for tax purposes as
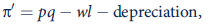
where depreciation is determined by governmental and industry guidelines that seek to allocate a machine's costs over its ''useful'' lifetime. If depreciation were equal to actual physical deterioration and if a firm were in long-run competitive equilibrium, how would a tax on
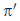 affect the firm's choice of capital inputs?
affect the firm's choice of capital inputs?
c. Given the conditions of part (b), describe how capital usage would be affected by adoption of ''accelerated depreciation'' policies, which specify depreciation rates in excess of physical deterioration early in a machine's life but much lower depreciation rates as the machine ages.
d. Under the conditions of part (c), how might a decrease in the corporate profits tax affect capital usage?
a. Suppose (contrary to fact) that profits were defined for tax purposes as what we have called pure economic profits. How would a tax on such profits affect investment decisions?
b. In fact, profits are defined for tax purposes as
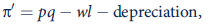
where depreciation is determined by governmental and industry guidelines that seek to allocate a machine's costs over its ''useful'' lifetime. If depreciation were equal to actual physical deterioration and if a firm were in long-run competitive equilibrium, how would a tax on
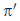 affect the firm's choice of capital inputs?
affect the firm's choice of capital inputs?c. Given the conditions of part (b), describe how capital usage would be affected by adoption of ''accelerated depreciation'' policies, which specify depreciation rates in excess of physical deterioration early in a machine's life but much lower depreciation rates as the machine ages.
d. Under the conditions of part (c), how might a decrease in the corporate profits tax affect capital usage?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
6
A high-pressure life insurance salesman was heard to make the following argument: ''At your age a $100,000 whole life policy is a much better buy than a similar term policy. Under a whole life policy you'll have to pay $2,000 per year for the first four years but nothing more for the rest of your life. A term policy will cost you $400 per year, essentially forever. If you live 35 years, you'll pay only $8,000 for the whole life policy, but $14,000 (¼ $400 Æ 35) for the term policy. Surely, the whole life is a better deal.'' Assuming the salesman's life expectancy assumption is correct, how would you evaluate this argument? Specifically, calculate the present discounted value of the premium costs of the two policies assuming the interest rate is 10 percent.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose that a perfect substitute for crude oil will be discovered in 15 years and that the price of this substitute will be the equivalent of an oil price of $125 per barrel. Suppose the current marginal extraction cost for oil is $7 per barrel. Assume also that the real interest rate is 5 percent and that real extraction costs decrease at a rate of 2 percent annually. If crude oil prices follow the path described in Equation 17.66, what should the current price of crude oil be? Does your answer shed any light on actual pricing in the crude oil market?
Reference: Equation 17.66

Reference: Equation 17.66


Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
8
Capital gains taxation
Suppose an individual has W dollars to allocate between consumption this period (c 0 ) and consumption next period (c 1 ) and that the interest rate is given by r.
a. Graph the individual's initial equilibrium and indicate the total value of current-period savings ( W - c 0 ).
b. Suppose that, after the individual makes his or her savings decision (by purchasing one-period bonds), the interest rate decreases to r '. How will this alter the individual's budget constraint? Show the new utility-maximizing position. Discuss how the individual's improved position can be interpreted as resulting from a ''capital gain'' on his or her initial bond purchases.
c. Suppose the tax authorities wish to impose an ''income'' tax based on the value of capital gains. If all such gains are valued in terms of c 0 as they are ''accrued,'' show how those gains should be measured. Call this value G 1.
d. Suppose instead that capital gains are measured as they are ''realized''-that is, capital gains are defined to include only that portion of bonds that is cashed in to buy additional c 0. Show how these realized gains can be measured. Call this amount G 2.
e. Develop a measure of the true increase in utility that results from the decrease in r, measured in terms of c 0. Call this ''true'' capital gain G 3. Show that G 3 G 2 G 1. What do you conclude about a tax policy that taxes only realized gains?
Note: This problem is adapted from J. Whalley, ''Capital Gains Taxation and Interest Rate Changes,'' National Tax Journal (March 1979): 87-91.
Suppose an individual has W dollars to allocate between consumption this period (c 0 ) and consumption next period (c 1 ) and that the interest rate is given by r.
a. Graph the individual's initial equilibrium and indicate the total value of current-period savings ( W - c 0 ).
b. Suppose that, after the individual makes his or her savings decision (by purchasing one-period bonds), the interest rate decreases to r '. How will this alter the individual's budget constraint? Show the new utility-maximizing position. Discuss how the individual's improved position can be interpreted as resulting from a ''capital gain'' on his or her initial bond purchases.
c. Suppose the tax authorities wish to impose an ''income'' tax based on the value of capital gains. If all such gains are valued in terms of c 0 as they are ''accrued,'' show how those gains should be measured. Call this value G 1.
d. Suppose instead that capital gains are measured as they are ''realized''-that is, capital gains are defined to include only that portion of bonds that is cashed in to buy additional c 0. Show how these realized gains can be measured. Call this amount G 2.
e. Develop a measure of the true increase in utility that results from the decrease in r, measured in terms of c 0. Call this ''true'' capital gain G 3. Show that G 3 G 2 G 1. What do you conclude about a tax policy that taxes only realized gains?
Note: This problem is adapted from J. Whalley, ''Capital Gains Taxation and Interest Rate Changes,'' National Tax Journal (March 1979): 87-91.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
9
Precautionary saving and prudence
The Query to Example 17.2 asks how uncertainty about the future might affect a person's savings decisions. In this problem we explore this question more fully. All of our analysis is based on the simple two-period model in Example 17.1.
a. To simplify matters, assume that
 in Equation 17.15. If consumption is certain, this implies that
in Equation 17.15. If consumption is certain, this implies that
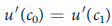 or
or
 . But suppose that consumption in period 1 will be subject to a zero-mean random shock, so that
. But suppose that consumption in period 1 will be subject to a zero-mean random shock, so that
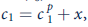 , where
, where
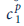 is planned period-1 consumption and x is a random variable with an expected value of 0. Describe why, in this context, utility maximization requires
is planned period-1 consumption and x is a random variable with an expected value of 0. Describe why, in this context, utility maximization requires
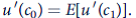
b. Use Jensen's inequality (see Chapters 2 and 7) to show that this person will opt for
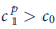 if and only if u' is convex-that is, if and only if u''' 0.
if and only if u' is convex-that is, if and only if u''' 0.
c. Kimball14 suggests using the term ''prudence'' to describe a person whose utility function is characterized by u''' 0.
Describe why the results from part (b) show that such a definition is consistent with everyday usage.
d. In Example 17.2 we showed that real interest rates in the U.S. economy seem too low to reconcile actual consumption growth rates with evidence on individuals' willingness to experience consumption fluctuations. If consumption growth rates were uncertain, would this explain or exacerbate the paradox?
The Query to Example 17.2 asks how uncertainty about the future might affect a person's savings decisions. In this problem we explore this question more fully. All of our analysis is based on the simple two-period model in Example 17.1.
a. To simplify matters, assume that
 in Equation 17.15. If consumption is certain, this implies that
in Equation 17.15. If consumption is certain, this implies that 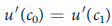 or
or  . But suppose that consumption in period 1 will be subject to a zero-mean random shock, so that
. But suppose that consumption in period 1 will be subject to a zero-mean random shock, so that 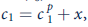 , where
, where 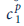 is planned period-1 consumption and x is a random variable with an expected value of 0. Describe why, in this context, utility maximization requires
is planned period-1 consumption and x is a random variable with an expected value of 0. Describe why, in this context, utility maximization requires 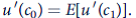
b. Use Jensen's inequality (see Chapters 2 and 7) to show that this person will opt for
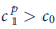 if and only if u' is convex-that is, if and only if u''' 0.
if and only if u' is convex-that is, if and only if u''' 0.c. Kimball14 suggests using the term ''prudence'' to describe a person whose utility function is characterized by u''' 0.
Describe why the results from part (b) show that such a definition is consistent with everyday usage.
d. In Example 17.2 we showed that real interest rates in the U.S. economy seem too low to reconcile actual consumption growth rates with evidence on individuals' willingness to experience consumption fluctuations. If consumption growth rates were uncertain, would this explain or exacerbate the paradox?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
10
Monopoly and natural resource prices
Suppose that a firm is the sole owner of a stock of a natural resource.
a. How should the analysis of the maximization of the discounted profits from selling this resource (Equation 17.58) be modified to take this fact into account?
b. Suppose that the demand for the resource in question had a constant elasticity form q(t) = a[p(t)] b. How would this change the price dynamics shown in Equation 17.62?
c. How would the answer to Problem 17.7 be changed if the entire crude oil supply were owned by a single firm?
Reference: Equation 17.58.17.62.17.7
![Monopoly and natural resource prices Suppose that a firm is the sole owner of a stock of a natural resource. a. How should the analysis of the maximization of the discounted profits from selling this resource (Equation 17.58) be modified to take this fact into account? b. Suppose that the demand for the resource in question had a constant elasticity form q(t) = a[p(t)] b. How would this change the price dynamics shown in Equation 17.62? c. How would the answer to Problem 17.7 be changed if the entire crude oil supply were owned by a single firm? Reference: Equation 17.58.17.62.17.7](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c8_d675_adfc_afd22fb12fb1_SM3017_11.jpg)
![Monopoly and natural resource prices Suppose that a firm is the sole owner of a stock of a natural resource. a. How should the analysis of the maximization of the discounted profits from selling this resource (Equation 17.58) be modified to take this fact into account? b. Suppose that the demand for the resource in question had a constant elasticity form q(t) = a[p(t)] b. How would this change the price dynamics shown in Equation 17.62? c. How would the answer to Problem 17.7 be changed if the entire crude oil supply were owned by a single firm? Reference: Equation 17.58.17.62.17.7](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c8_d676_adfc_195e9534df52_SM3017_11.jpg)
![Monopoly and natural resource prices Suppose that a firm is the sole owner of a stock of a natural resource. a. How should the analysis of the maximization of the discounted profits from selling this resource (Equation 17.58) be modified to take this fact into account? b. Suppose that the demand for the resource in question had a constant elasticity form q(t) = a[p(t)] b. How would this change the price dynamics shown in Equation 17.62? c. How would the answer to Problem 17.7 be changed if the entire crude oil supply were owned by a single firm? Reference: Equation 17.58.17.62.17.7](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c8_fd87_adfc_ef8b141c5047_SM3017_11.jpg)
Suppose that a firm is the sole owner of a stock of a natural resource.
a. How should the analysis of the maximization of the discounted profits from selling this resource (Equation 17.58) be modified to take this fact into account?
b. Suppose that the demand for the resource in question had a constant elasticity form q(t) = a[p(t)] b. How would this change the price dynamics shown in Equation 17.62?
c. How would the answer to Problem 17.7 be changed if the entire crude oil supply were owned by a single firm?
Reference: Equation 17.58.17.62.17.7
![Monopoly and natural resource prices Suppose that a firm is the sole owner of a stock of a natural resource. a. How should the analysis of the maximization of the discounted profits from selling this resource (Equation 17.58) be modified to take this fact into account? b. Suppose that the demand for the resource in question had a constant elasticity form q(t) = a[p(t)] b. How would this change the price dynamics shown in Equation 17.62? c. How would the answer to Problem 17.7 be changed if the entire crude oil supply were owned by a single firm? Reference: Equation 17.58.17.62.17.7](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c8_d675_adfc_afd22fb12fb1_SM3017_11.jpg)
![Monopoly and natural resource prices Suppose that a firm is the sole owner of a stock of a natural resource. a. How should the analysis of the maximization of the discounted profits from selling this resource (Equation 17.58) be modified to take this fact into account? b. Suppose that the demand for the resource in question had a constant elasticity form q(t) = a[p(t)] b. How would this change the price dynamics shown in Equation 17.62? c. How would the answer to Problem 17.7 be changed if the entire crude oil supply were owned by a single firm? Reference: Equation 17.58.17.62.17.7](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c8_d676_adfc_195e9534df52_SM3017_11.jpg)
![Monopoly and natural resource prices Suppose that a firm is the sole owner of a stock of a natural resource. a. How should the analysis of the maximization of the discounted profits from selling this resource (Equation 17.58) be modified to take this fact into account? b. Suppose that the demand for the resource in question had a constant elasticity form q(t) = a[p(t)] b. How would this change the price dynamics shown in Equation 17.62? c. How would the answer to Problem 17.7 be changed if the entire crude oil supply were owned by a single firm? Reference: Equation 17.58.17.62.17.7](https://d2lvgg3v3hfg70.cloudfront.net/SM3017/11eb773e_d1c8_fd87_adfc_ef8b141c5047_SM3017_11.jpg)

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
11
Renewable timber economics
The calculations in Problem 17.4 assume there is no difference between the decisions to cut a single tree and to manage a woodlot. But managing a woodlot also involves replanting, which should be explicitly modeled. To do so, assume a lot owner is considering planting a single tree at a cost w, harvesting the tree at t * , planting another, and so forth forever. The discounted stream of profits from this activity is then
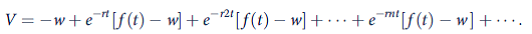
a. Show that the total value of this planned harvesting activity is given by

b. Find the value of t that maximizes V. Show that this value solves the equation
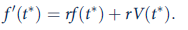
c. Interpret the results of part (b): How do they reflect optimal usage of the ''input'' time? Why is the value of t * specified in part (b) different from that in Example 17.2?
d. Suppose tree growth (measured in constant dollars) follows the logistic function

What is the maximum value of the timber available from this tree?
e. If tree growth is characterized by the equation given in part (d), what is the optimal rotation period if r = 0.05 and w = 0? Does this period produce a ''maximum sustainable'' yield?
f. How would the optimal period change if r decreased to 0.04?
Note: The equation derived in part (b) is known in forestry economics as Faustmann's equation.
The calculations in Problem 17.4 assume there is no difference between the decisions to cut a single tree and to manage a woodlot. But managing a woodlot also involves replanting, which should be explicitly modeled. To do so, assume a lot owner is considering planting a single tree at a cost w, harvesting the tree at t * , planting another, and so forth forever. The discounted stream of profits from this activity is then
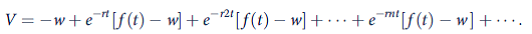
a. Show that the total value of this planned harvesting activity is given by

b. Find the value of t that maximizes V. Show that this value solves the equation
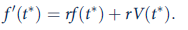
c. Interpret the results of part (b): How do they reflect optimal usage of the ''input'' time? Why is the value of t * specified in part (b) different from that in Example 17.2?
d. Suppose tree growth (measured in constant dollars) follows the logistic function

What is the maximum value of the timber available from this tree?
e. If tree growth is characterized by the equation given in part (d), what is the optimal rotation period if r = 0.05 and w = 0? Does this period produce a ''maximum sustainable'' yield?
f. How would the optimal period change if r decreased to 0.04?
Note: The equation derived in part (b) is known in forestry economics as Faustmann's equation.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
12
Hyperbolic discounting
The notion that people might be ''shortsighted'' was formalized by David Laibson in ''Golden Eggs and Hyperbolic Discounting'' (Quarterly Journal of Economics, May 1997, pp. 443-77). In this paper the author hypothesizes that individuals maximize an intertemporal utility function of the form
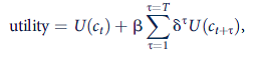
where
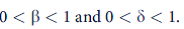 . The particular time pattern of these discount factors leads to the possibility of shortsightedness.
. The particular time pattern of these discount factors leads to the possibility of shortsightedness.
a. Laibson suggests hypothetical values of ? = 0.6 and ? = 0.99. Show that, for these values, the factors by which future consumption is discounted follow a general hyperbolic pattern. That is, show that the factors decrease significantly for period t + 1 and then follow a steady geometric rate of decrease for subsequent periods.
b. Describe intuitively why this pattern of discount rates might lead to shortsighted behavior.
c. More formally, calculate the MRS between c t + 1 and c t + 2 at time t. Compare this to the MRS between c t + 1 and c t + 2 at time t + 1. Explain why, with a constant real interest rate, this would imply ''dynamically inconsistent'' choices over time. Specifically, how would the relationship between optimal c t + 1 and c t + 2 differ from these two perspectives?
d. Laibson explains that the pattern described in part (c) will lead ''early selves'' to find ways to constrain ''future selves'' and so achieve full utility maximization. Explain why such constraints are necessary.
e. Describe a few of the ways in which people seek to constrain their future choices in the real world.
The notion that people might be ''shortsighted'' was formalized by David Laibson in ''Golden Eggs and Hyperbolic Discounting'' (Quarterly Journal of Economics, May 1997, pp. 443-77). In this paper the author hypothesizes that individuals maximize an intertemporal utility function of the form
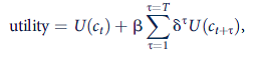
where
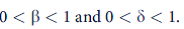 . The particular time pattern of these discount factors leads to the possibility of shortsightedness.
. The particular time pattern of these discount factors leads to the possibility of shortsightedness.a. Laibson suggests hypothetical values of ? = 0.6 and ? = 0.99. Show that, for these values, the factors by which future consumption is discounted follow a general hyperbolic pattern. That is, show that the factors decrease significantly for period t + 1 and then follow a steady geometric rate of decrease for subsequent periods.
b. Describe intuitively why this pattern of discount rates might lead to shortsighted behavior.
c. More formally, calculate the MRS between c t + 1 and c t + 2 at time t. Compare this to the MRS between c t + 1 and c t + 2 at time t + 1. Explain why, with a constant real interest rate, this would imply ''dynamically inconsistent'' choices over time. Specifically, how would the relationship between optimal c t + 1 and c t + 2 differ from these two perspectives?
d. Laibson explains that the pattern described in part (c) will lead ''early selves'' to find ways to constrain ''future selves'' and so achieve full utility maximization. Explain why such constraints are necessary.
e. Describe a few of the ways in which people seek to constrain their future choices in the real world.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck



