Deck 16: Ascii Character Set
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
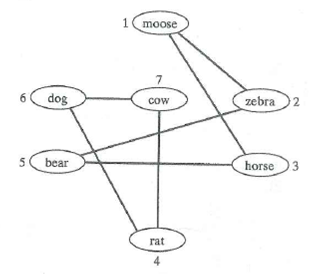
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/110
Play
Full screen (f)
Deck 16: Ascii Character Set
1
Write a program to test the breadth-first search function in Exercise 20.
Problem Plan:
• Include the necessary header files that are referred to as this program will use list, vector, queue, etc. data structures. Thus, at least C++11 is required for compilation of this program.
• Include only the required parts of the header file into the program (that is the provided "Digraph.h"). Thus this file must hold the required function definition of breadth-first search as this tester program will test that function in following programming exercise.
o Define the "main()" function as this is the sole of the required tester program.
o Define string variable "fileNameGraph" for file name.
o Prompt user to enter the file name that contains the graph details.
• Get the value for file name from the user.
o Use "ifstream" for input file with a relevant name say, "fileGraph".
• Exit the program on wrong data; mentioning the issue.
o Now a digraph can be initialized inside the program namely, graph.
• Populate the graph from the given file.
o Prompt user to enter the start vertex for the BFS of the given graph.
• Get the value for start vertex in a relevantly named variable say, "startsAt".
• Call the exact function on the digraph that was built earlier in Exercise 20 of 16.2.
Program:
/ *********************************************************** This tester program is intended to test the function * * that was derived in Exercise 20 of 16.2. In simpler * * words, this program will subject a given graph to * * breadth-first search from a given start vertex. In order* * to process the following vertices in that trace tree, it* * will simply print the data held by that vertex following* * the order it visits them. *
* *
* The graph, as usual, is taken from a file as input, * * thus, the input to this program are: *
* The name of file containing graph details *
* The start vertex (vertex labeling) for breadth-first * * search. *
********************************************************** /
/ / Header file for list handling
#include
/ / Header file for vector handling
#include
/ / Header file for queue handling
#include
/ * Header file for handling the standard functions related to i / o * /
#include
/ / Header file for file stream handling
#include
/ / the standard namespace to be used
using namespace std;
/ * Defining the Digraph class template * /
template
/ * Only the required function are added to test the mentioned function * /
class Digraph
{
/ * The function prototypes for the members that are defined here; They're all public * /
public:
/ * It reads from the input file stream to the program heap * /
void read(ifstream inFileStrm);
/ * It finds the BFS trace tree for a given start vertex, i.e. return a spanning tree if the graph is all connected from the given start vertex or return a forest with a single tree * /
void funBFS(int startVertex); / / The function prototype for breadth-first search
/ * The member variable to be declared here; They're all private * /
private:
class VertexInfo { / / The exact definition as was there
public:
DataType data; / / holds the data
list adjacencyList; / / shows the connected vertices' label
};
vector myAdjacencyLists; / / The array of vertices that further contains the lists of endpoints
}; / / Class definition ends here
/ / Function definition is given here for read()
template
void Digraph ::read(ifstream inFileStrm)
{
/ *reads from the input file stream* /
Digraph ::VertexInfo vi; / / variables to be used
int n, aVertex; / / for connections and vertices' label
myAdjacencyLists.push_back(vi); / / The exact way to maintain 1 indexing
for (;;) { / / Infinite loop using for
inFileStrm vi.data; / / feeding the data value
if (inFileStrm.eof()) break; / / The loop breaking condition; till the end of the file stream
inFileStrm n; / / # of connections from the vertex
list adjList;
for (int i = 1; i = n; i++) { / / For those connections the list is built
inFileStrm aVertex; / / The endpoints
adjList.push_back(aVertex); / / are fed to the list
}
vi.adjacencyList = adjList; / / The built adjacency list is assigned to proper vertex
myAdjacencyLists.push_back(vi); / / Then the vertex is pushed to the list of vertex
} / / End of for loop
} / / Ends here
/ *
* This algorithm is for a digraph to perform breadth search algorithm as mentioned
* It uses concept of queue for processing vertices in the graph.
* It starts with a given start vertex, hence that is fed as the only input.
* It either derives a forest with a single tree that starts from the mentioned start vertex or form a spanning tree of the given graph subject to connectivity of the vertices in the graph.
* The below function prototype must be mentioned inside the class template (public member) in Digraph.h file.
* /
template
void Digraph ::funBFS(int startVertex)
{ / / Function definition for breadth-first search
/ * Start by printing (i.e. processing) v[startVertex].data as it gets visited by default * /
cout myAdjacencyLists[startVertex].data endl;
/ * Initialize a queue with the start vertex * /
queue q;
q.push(myAdjacencyLists[startVertex]);
/ * Mark all vertices as unvisited by default * /
vector unVisitedVertex(myAdjacencyLists.size(), true);
/ * The start vertex must be marked as visited at the very start * /
unVisitedVertex[startVertex] = false;
/ * Unless the queue becomes empty repeat * /
while (!q.empty())
{
/ * Remove a vertex from queue-front and denote it by v * /
VertexInfo v = q.front();
q.pop();
/ * Go through its neighbors and process them as following instruction * /
for (list ::iterator neighbor = v.adjacencyList.begin(); neighbor != v.adjacencyList.end(); neighbor++) {
/ * Take following action if the neighbor is unvisited * /
if (unVisitedVertex[*neighbor]) {
/ * Print it (i.e. processing) and mark as unvisited * /
cout myAdjacencyLists [*neighbor].data endl;
unVisitedVertex[*neighbor] = false;
/ * Insert it to the queue-rear * /
q.push(myAdjacencyLists[*neighbor]);
} / / End of if
} / / End of for-loop
} / / End of while-loop
} / / End of function
/ * The main program starts here; It will test the above mentioned functions * /
int main()
{
/ * Required string variable for holding the filename is declared here* /
string fileNameGraph;
/ * Prompt user for input then, acquire them accordingly * /
cout "Enter name of the file that contains the graph details: ";
cin fileNameGraph;
/ * ifstream for the input file * /
ifstream fileGraph(fileNameGraph.data());
if (!fileGraph.is_open()) { / / If the mentioned file cannot be found / opened due to any reason
/ * Show error and then exit the program * /
cout "ERROR: " fileNameGraph " cannot be opened!\n";
exit(-1); / / '-1' to notify unsuccessful execution
}
/ * Required digraph variable is declared here, then populated from the file * /
Digraph graph;
graph.read(fileGraph);
/ * Prompt user for input then, acquire them accordingly * /
cout "Which vertex to start from: ";
/ * Required integer variable is declared here, to hold the label of start vertex * /
int startsAt;
cin startsAt;
/ * Call the required function * /
graph.funBFS(startsAt);
} / / Done
Sample Input:
Graph.txt
cat3 2 4 6zebra1 3horse1 2rat3 1 3 5bear2 2 3dog4 1 2 3 5
Sample Output (1):
Enter name of the file that contains the graph details: Graph.txt
Which vertex to start from: 1
cat
zebra
rat
dog
horse
bear
Sample Output (2):
Enter name of the file that contains the graph details: Graph.txt
Which vertex to start from: 2
zebra
horse
• Include the necessary header files that are referred to as this program will use list, vector, queue, etc. data structures. Thus, at least C++11 is required for compilation of this program.
• Include only the required parts of the header file into the program (that is the provided "Digraph.h"). Thus this file must hold the required function definition of breadth-first search as this tester program will test that function in following programming exercise.
o Define the "main()" function as this is the sole of the required tester program.
o Define string variable "fileNameGraph" for file name.
o Prompt user to enter the file name that contains the graph details.
• Get the value for file name from the user.
o Use "ifstream" for input file with a relevant name say, "fileGraph".
• Exit the program on wrong data; mentioning the issue.
o Now a digraph can be initialized inside the program namely, graph.
• Populate the graph from the given file.
o Prompt user to enter the start vertex for the BFS of the given graph.
• Get the value for start vertex in a relevantly named variable say, "startsAt".
• Call the exact function on the digraph that was built earlier in Exercise 20 of 16.2.
Program:
/ *********************************************************** This tester program is intended to test the function * * that was derived in Exercise 20 of 16.2. In simpler * * words, this program will subject a given graph to * * breadth-first search from a given start vertex. In order* * to process the following vertices in that trace tree, it* * will simply print the data held by that vertex following* * the order it visits them. *
* *
* The graph, as usual, is taken from a file as input, * * thus, the input to this program are: *
* The name of file containing graph details *
* The start vertex (vertex labeling) for breadth-first * * search. *
********************************************************** /
/ / Header file for list handling
#include
/ / Header file for vector handling
#include
/ / Header file for queue handling
#include
/ * Header file for handling the standard functions related to i / o * /
#include
/ / Header file for file stream handling
#include
/ / the standard namespace to be used
using namespace std;
/ * Defining the Digraph class template * /
template
/ * Only the required function are added to test the mentioned function * /
class Digraph
{
/ * The function prototypes for the members that are defined here; They're all public * /
public:
/ * It reads from the input file stream to the program heap * /
void read(ifstream inFileStrm);
/ * It finds the BFS trace tree for a given start vertex, i.e. return a spanning tree if the graph is all connected from the given start vertex or return a forest with a single tree * /
void funBFS(int startVertex); / / The function prototype for breadth-first search
/ * The member variable to be declared here; They're all private * /
private:
class VertexInfo { / / The exact definition as was there
public:
DataType data; / / holds the data
list adjacencyList; / / shows the connected vertices' label
};
vector myAdjacencyLists; / / The array of vertices that further contains the lists of endpoints
}; / / Class definition ends here
/ / Function definition is given here for read()
template
void Digraph ::read(ifstream inFileStrm)
{
/ *reads from the input file stream* /
Digraph ::VertexInfo vi; / / variables to be used
int n, aVertex; / / for connections and vertices' label
myAdjacencyLists.push_back(vi); / / The exact way to maintain 1 indexing
for (;;) { / / Infinite loop using for
inFileStrm vi.data; / / feeding the data value
if (inFileStrm.eof()) break; / / The loop breaking condition; till the end of the file stream
inFileStrm n; / / # of connections from the vertex
list adjList;
for (int i = 1; i = n; i++) { / / For those connections the list is built
inFileStrm aVertex; / / The endpoints
adjList.push_back(aVertex); / / are fed to the list
}
vi.adjacencyList = adjList; / / The built adjacency list is assigned to proper vertex
myAdjacencyLists.push_back(vi); / / Then the vertex is pushed to the list of vertex
} / / End of for loop
} / / Ends here
/ *
* This algorithm is for a digraph to perform breadth search algorithm as mentioned
* It uses concept of queue for processing vertices in the graph.
* It starts with a given start vertex, hence that is fed as the only input.
* It either derives a forest with a single tree that starts from the mentioned start vertex or form a spanning tree of the given graph subject to connectivity of the vertices in the graph.
* The below function prototype must be mentioned inside the class template (public member) in Digraph.h file.
* /
template
void Digraph ::funBFS(int startVertex)
{ / / Function definition for breadth-first search
/ * Start by printing (i.e. processing) v[startVertex].data as it gets visited by default * /
cout myAdjacencyLists[startVertex].data endl;
/ * Initialize a queue with the start vertex * /
queue q;
q.push(myAdjacencyLists[startVertex]);
/ * Mark all vertices as unvisited by default * /
vector unVisitedVertex(myAdjacencyLists.size(), true);
/ * The start vertex must be marked as visited at the very start * /
unVisitedVertex[startVertex] = false;
/ * Unless the queue becomes empty repeat * /
while (!q.empty())
{
/ * Remove a vertex from queue-front and denote it by v * /
VertexInfo v = q.front();
q.pop();
/ * Go through its neighbors and process them as following instruction * /
for (list ::iterator neighbor = v.adjacencyList.begin(); neighbor != v.adjacencyList.end(); neighbor++) {
/ * Take following action if the neighbor is unvisited * /
if (unVisitedVertex[*neighbor]) {
/ * Print it (i.e. processing) and mark as unvisited * /
cout myAdjacencyLists [*neighbor].data endl;
unVisitedVertex[*neighbor] = false;
/ * Insert it to the queue-rear * /
q.push(myAdjacencyLists[*neighbor]);
} / / End of if
} / / End of for-loop
} / / End of while-loop
} / / End of function
/ * The main program starts here; It will test the above mentioned functions * /
int main()
{
/ * Required string variable for holding the filename is declared here* /
string fileNameGraph;
/ * Prompt user for input then, acquire them accordingly * /
cout "Enter name of the file that contains the graph details: ";
cin fileNameGraph;
/ * ifstream for the input file * /
ifstream fileGraph(fileNameGraph.data());
if (!fileGraph.is_open()) { / / If the mentioned file cannot be found / opened due to any reason
/ * Show error and then exit the program * /
cout "ERROR: " fileNameGraph " cannot be opened!\n";
exit(-1); / / '-1' to notify unsuccessful execution
}
/ * Required digraph variable is declared here, then populated from the file * /
Digraph graph;
graph.read(fileGraph);
/ * Prompt user for input then, acquire them accordingly * /
cout "Which vertex to start from: ";
/ * Required integer variable is declared here, to hold the label of start vertex * /
int startsAt;
cin startsAt;
/ * Call the required function * /
graph.funBFS(startsAt);
} / / Done
Sample Input:
Graph.txt
cat3 2 4 6zebra1 3horse1 2rat3 1 3 5bear2 2 3dog4 1 2 3 5
Sample Output (1):
Enter name of the file that contains the graph details: Graph.txt
Which vertex to start from: 1
cat
zebra
rat
dog
horse
bear
Sample Output (2):
Enter name of the file that contains the graph details: Graph.txt
Which vertex to start from: 2
zebra
horse
2
Write a program to test the reachability-matrix function in Exercise 21.
Program Plan:
• Keep only the required header that is to be used (iostream for standard I / O operations). Then, use the standard namespace.
• Create a 2-D array of dimension equal to the digraph and populate it with the graph's adjacency details.
• Create another 2-D array of same dimension as above and set it to identity matrix (i.e. all diagonal set to 1 and zeroes off).
• Perform repeated addition and multiplication of the adjacency matrix to the identity matrix as created above. Then assign it to reachability matrix. This should be repeated the exact count as the vertices in the digraph.
Program:
/ * This program Finds the reachability matrix of given *
* digraph that is fed by its adjacency matrix of dimension*
* of the count of vertices in itself * /
/ / Inclusion of header for standard I / O operation
#include
/ / The standard namespace is being used
using namespace std;
int **addMatrix (int **firstMatrix, int **secondMatrix, int dimension)
{
/ * Used for adding two matrices of given dimension * /
int **sumMat = new int *[dimension]; / / defining the row count of matrix
/ / Read values of all the rows
for (int row = 0; row dimension; row++)
/ / Allocate memory for all entries in array
sumMat[row] = new int[dimension];
/ / Read values of all the rows
for (int row = 0; row dimension; row++)
/ / Read values of all the columns
for (int column = 0; column dimension; column++)
/ *Find the sum of corresponding locations in matrix * /
sumMat[row][column] = firstMatrix[row][column] + secondMatrix[row][column];
/ / return the sum of two matrices of given dimension
return sumMat;
}
int **multiplyMatrix(int **firstMatrix, int **secondMatrix, int dimension)
{
/ * Used for multiplying two matrices of given dimension and defining the row count of matrix * /
int **productMat = new int *[dimension];
/ / Read values of all the rows
for (int row = 0; row dimension; row++)
/ / Allocate memory for all entries in array
productMat[row] = new int[dimension];
/ / Read values of all the rows
for (int row = 0; row dimension; row++)
/ / Read values of all the columns
for (int column = 0; column dimension; column++)
{
/ / Each time need to be set to zero
int sum = 0;
for (int k = 0; k dimension; k++)
{
/ *Find the products of corresponding locations in matrices * /
sum += firstMatrix[row][k] * secondMatrix[k][column];
}
/ / The elements at the result matrix
productMat[row][column] = sum;
}
/ * The result of the multiplication of two matrices of given dimension * /
return productMat;
}
/ / Function declaration
int **reachabilityMatrix(int **adjMat, int dimension)
{
/ * Used for finding the reachability matrix of given dimension for a graph represented by the given adjacency matrix; The dimension here is actually the count of vertices thus the dimension of reachability matrix is as same as adjacency matrix * /
int **reachMat = new int *[dimension];
/ / to create an identity matrix
int **idMat = new int *[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
{
/ / Allocate memory for all entries in array
reachMat[row] = new int[dimension];
/ / Allocate memory for all entries in array
idMat[row] = new int[dimension];
/ / And creating an identity matrix
idMat[row][row] = 1;
}
/ / For all the vertices perform the following
for (int iterator = 0; iterator dimension; iterator++)
{
/ / addition of two matrices
reachMat = addMatrix(reachMat, idMat, dimension);
/ / multiplication of two matrices
idMat = multiplyMatrix(idMat, adjMat, dimension);
}
/ *The resultant matrix that represents the reachability matrix * /
return reachMat;
}
/ / Main function
int main()
{
/ / It holds the count of vertices in the graph
int countVertex;
/ / Prompt user for the count of vertices
cout "Enter the count of vertices: ";
/ / Holds the input for the count of vertices
cin countVertex;
/ *2-D matrices of dimension of count of vertices; represented by a pointer that will be passed on to functions * /
int **reachMatrix, **adjMatrix = new int *[countVertex];
/ / Initiate the adjacency matrix
for (int row = 0; row countVertex; row++)
/ * Making rooms for the entries in matrix by allocating space for an integer * /
adjMatrix[row] = new int[countVertex];
/ / Prompt to stdout for inputting the adjacency matrix
cout "Enter the adjacency matrix: " endl;
/ / For all the rows
for (int row = 0; row countVertex; row++)
/ / Then all the columns
for (int column = 0; column countVertex; column++)
/ *take input from the user to adjacency matrix * /
cin adjMatrix[row][column];
/ *Invoking the function for reachability matrix * /
reachMatrix = reachabilityMatrix(adjMatrix, countVertex);
/ / Notification for reachability matrix to stdout
cout "The corresponding reachability matrix: " endl;
/ / For all the rows
for (int row = 0; row countVertex; row++)
{
/ / Then all the columns
for (int column = 0; column countVertex; column++)
/ / Print the entry
cout reachMatrix[row][column] " ";
/ *At the end of a row, print a new line for a matrix like feeling * /
cout endl;
} / / End of for loop
return 0; / / For successful execution
} / / Ends here
Sample Output:
Enter the count of vertices: 5
Enter the adjacency matrix:
0 1 1 0 1
0 0 1 0 0
0 1 0 1 0
0 0 0 1 0
0 0 0 0 0
The corresponding reachability matrix:
1 4 4 6 1
0 3 2 4 0
0 2 3 6 0
0 0 0 5 0
0 0 0 0 1
• Keep only the required header that is to be used (iostream for standard I / O operations). Then, use the standard namespace.
• Create a 2-D array of dimension equal to the digraph and populate it with the graph's adjacency details.
• Create another 2-D array of same dimension as above and set it to identity matrix (i.e. all diagonal set to 1 and zeroes off).
• Perform repeated addition and multiplication of the adjacency matrix to the identity matrix as created above. Then assign it to reachability matrix. This should be repeated the exact count as the vertices in the digraph.
Program:
/ * This program Finds the reachability matrix of given *
* digraph that is fed by its adjacency matrix of dimension*
* of the count of vertices in itself * /
/ / Inclusion of header for standard I / O operation
#include
/ / The standard namespace is being used
using namespace std;
int **addMatrix (int **firstMatrix, int **secondMatrix, int dimension)
{
/ * Used for adding two matrices of given dimension * /
int **sumMat = new int *[dimension]; / / defining the row count of matrix
/ / Read values of all the rows
for (int row = 0; row dimension; row++)
/ / Allocate memory for all entries in array
sumMat[row] = new int[dimension];
/ / Read values of all the rows
for (int row = 0; row dimension; row++)
/ / Read values of all the columns
for (int column = 0; column dimension; column++)
/ *Find the sum of corresponding locations in matrix * /
sumMat[row][column] = firstMatrix[row][column] + secondMatrix[row][column];
/ / return the sum of two matrices of given dimension
return sumMat;
}
int **multiplyMatrix(int **firstMatrix, int **secondMatrix, int dimension)
{
/ * Used for multiplying two matrices of given dimension and defining the row count of matrix * /
int **productMat = new int *[dimension];
/ / Read values of all the rows
for (int row = 0; row dimension; row++)
/ / Allocate memory for all entries in array
productMat[row] = new int[dimension];
/ / Read values of all the rows
for (int row = 0; row dimension; row++)
/ / Read values of all the columns
for (int column = 0; column dimension; column++)
{
/ / Each time need to be set to zero
int sum = 0;
for (int k = 0; k dimension; k++)
{
/ *Find the products of corresponding locations in matrices * /
sum += firstMatrix[row][k] * secondMatrix[k][column];
}
/ / The elements at the result matrix
productMat[row][column] = sum;
}
/ * The result of the multiplication of two matrices of given dimension * /
return productMat;
}
/ / Function declaration
int **reachabilityMatrix(int **adjMat, int dimension)
{
/ * Used for finding the reachability matrix of given dimension for a graph represented by the given adjacency matrix; The dimension here is actually the count of vertices thus the dimension of reachability matrix is as same as adjacency matrix * /
int **reachMat = new int *[dimension];
/ / to create an identity matrix
int **idMat = new int *[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
{
/ / Allocate memory for all entries in array
reachMat[row] = new int[dimension];
/ / Allocate memory for all entries in array
idMat[row] = new int[dimension];
/ / And creating an identity matrix
idMat[row][row] = 1;
}
/ / For all the vertices perform the following
for (int iterator = 0; iterator dimension; iterator++)
{
/ / addition of two matrices
reachMat = addMatrix(reachMat, idMat, dimension);
/ / multiplication of two matrices
idMat = multiplyMatrix(idMat, adjMat, dimension);
}
/ *The resultant matrix that represents the reachability matrix * /
return reachMat;
}
/ / Main function
int main()
{
/ / It holds the count of vertices in the graph
int countVertex;
/ / Prompt user for the count of vertices
cout "Enter the count of vertices: ";
/ / Holds the input for the count of vertices
cin countVertex;
/ *2-D matrices of dimension of count of vertices; represented by a pointer that will be passed on to functions * /
int **reachMatrix, **adjMatrix = new int *[countVertex];
/ / Initiate the adjacency matrix
for (int row = 0; row countVertex; row++)
/ * Making rooms for the entries in matrix by allocating space for an integer * /
adjMatrix[row] = new int[countVertex];
/ / Prompt to stdout for inputting the adjacency matrix
cout "Enter the adjacency matrix: " endl;
/ / For all the rows
for (int row = 0; row countVertex; row++)
/ / Then all the columns
for (int column = 0; column countVertex; column++)
/ *take input from the user to adjacency matrix * /
cin adjMatrix[row][column];
/ *Invoking the function for reachability matrix * /
reachMatrix = reachabilityMatrix(adjMatrix, countVertex);
/ / Notification for reachability matrix to stdout
cout "The corresponding reachability matrix: " endl;
/ / For all the rows
for (int row = 0; row countVertex; row++)
{
/ / Then all the columns
for (int column = 0; column countVertex; column++)
/ / Print the entry
cout reachMatrix[row][column] " ";
/ *At the end of a row, print a new line for a matrix like feeling * /
cout endl;
} / / End of for loop
return 0; / / For successful execution
} / / Ends here
Sample Output:
Enter the count of vertices: 5
Enter the adjacency matrix:
0 1 1 0 1
0 0 1 0 0
0 1 0 1 0
0 0 0 1 0
0 0 0 0 0
The corresponding reachability matrix:
1 4 4 6 1
0 3 2 4 0
0 2 3 6 0
0 0 0 5 0
0 0 0 0 1
3
Write a program to test the boolean reachability-matrix function in Exercise 22.
Program Plan:
• Keep only the required header that is to be used (iostream for standard I / O operations). Then, use the standard namespace.
• Create a 2-D array of dimension equal to the digraph and populate it with the graph's adjacency details.
• Create another 2-D array of same dimension as above and set it to identity matrix (i.e. all diagonal set to 1 and zeroes off).
• Perform repeated addition and multiplication of the adjacency matrix to the identity matrix as created above. Then assign it to reachability matrix. This should be repeated the exact count as the vertices in the digraph.
• This multiplication is in terms of Boolean operation, i.e. OR represents the addition whereas AND operation represents the multiplication.
Program:
/ * This program finds the Boolean reachability matrix of *
* given digraph that is fed by its adjacency matrix of *
* dimension of the count of vertices in itself * /
/ / Inclusion of header for standard I / O operation
#include
/ / The standard namespace is being used
using namespace std;
int **addMatrixBoolean(int **firstMatrix, int **secondMatrix, int dimension)
{
/ * Used for adding two matrices of given dimension * /
int **sumMat = new int *[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
/ / making rooms for all entries in array
sumMat[row] = new int[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
/ / Then all the columns
for (int column = 0; column dimension; column++)
/ / Find the Boolean OR
sumMat[row][column] = firstMatrix[row][column] || secondMatrix[row][column];
/ * return the Boolean sum of two matrices of given dimension * /
return sumMat;
}
/ / Function definition
int **multiplyMatrixBoolean(int **firstMatrix, int **secondMatrix, int dimension)
{
/ * Used for multiplying two matrices of given dimension * /
int **productMat = new int *[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
/ / making rooms for all entries in array
productMat[row] = new int[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
/ / Then all the columns
for (int column = 0; column dimension; column++)
{
/ / Each time need to be set to zero
int sum = 0;
for (int k = 0; k dimension; k++)
{
/ / The Boolean OR, AND operation
sum |= firstMatrix[row][k] secondMatrix[k][column];
}
/ / The elements at the result matrix
productMat[row][column] = sum;
}
/ * The result of the multiplication of two matrices of given dimension * /
return productMat;
}
/ / Function definition
int **reachabilityMatrix(int **adjMat, int dimension)
{
/ * Used for finding the Boolean reachability matrix of given dimension for a graph represented by the given adjacency matrix; The dimension here is actually the count of vertices thus the dimension of reachability matrix is as same as adjacency matrix * /
int **reachMat = new int *[dimension];
/ / to create an identity matrix
int **idMat = new int *[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
{
/ / making rooms for all entries in array
reachMat[row] = new int[dimension];
/ / making rooms for all entries in array
idMat[row] = new int[dimension];
/ / And creating an identity matrix
idMat[row][row] = 1;
}
/ / For all the vertices perform the following
for (int iterator = 0; iterator dimension; iterator++)
{
/ / addition of two matrices
reachMat = addMatrixBoolean(reachMat, idMat, dimension);
/ / multiplication of two matrices
idMat = multiplyMatrixBoolean(idMat, adjMat, dimension);
}
/ * The resultant matrix that represents the reachability matrix * /
return reachMat;
}
/ / Main function
int main()
{
/ / It holds the count of vertices in the graph
int countVertex;
/ / Prompt user for the count of vertices
cout "Enter the count of vertices: ";
/ / Holds the input for the count of vertices
cin countVertex;
/ *2-D matrices of dimension of count of vertices; represented by a pointer that will be passed on to functions* /
int **reachMatrix, **adjMatrix = new int *[countVertex];
/ / Initiate the adjacency matrix
for (int row = 0; row countVertex; row++)
/ * Making rooms for the entries in matrix by allocating space for an integer * /
adjMatrix[row] = new int[countVertex];
/ / Prompt to stdout for inputting the adjacency matrix
cout "Enter the adjacency matrix: " endl;
/ / For all the rows
for (int row = 0; row countVertex; row++)
/ / Then all the columns
for (int column = 0; column countVertex; column++)
/ *take input from the user to adjacency matrix * /
cin adjMatrix[row][column];
/ / Invoking the function for reachability matrix
reachMatrix = reachabilityMatrix(adjMatrix, countVertex);
/ / Notification for reachability matrix to stdout
cout "The corresponding reachability matrix: " endl;
/ / For all the rows
for (int row = 0; row countVertex; row++)
{
/ / Then all the columns
for (int column = 0; column countVertex; column++)
/ / Print the entry
cout reachMatrix[row][column] " ";
/ *At the end of a row, print a new line for a matrix like form * /
cout endl;
} / / End of for loop
return 0; / / For successful execution
} / / Ends here
Sample Output:
Enter the count of vertices: 5
Enter the adjacency matrix:
0 1 1 0 1
0 0 1 0 0
0 1 0 1 0
0 0 0 1 0
0 0 0 0 0
The corresponding reachability matrix:
1 1 1 1 1
0 1 1 1 0
0 1 1 1 0
0 0 0 1 0
0 0 0 0 1
• Keep only the required header that is to be used (iostream for standard I / O operations). Then, use the standard namespace.
• Create a 2-D array of dimension equal to the digraph and populate it with the graph's adjacency details.
• Create another 2-D array of same dimension as above and set it to identity matrix (i.e. all diagonal set to 1 and zeroes off).
• Perform repeated addition and multiplication of the adjacency matrix to the identity matrix as created above. Then assign it to reachability matrix. This should be repeated the exact count as the vertices in the digraph.
• This multiplication is in terms of Boolean operation, i.e. OR represents the addition whereas AND operation represents the multiplication.
Program:
/ * This program finds the Boolean reachability matrix of *
* given digraph that is fed by its adjacency matrix of *
* dimension of the count of vertices in itself * /
/ / Inclusion of header for standard I / O operation
#include
/ / The standard namespace is being used
using namespace std;
int **addMatrixBoolean(int **firstMatrix, int **secondMatrix, int dimension)
{
/ * Used for adding two matrices of given dimension * /
int **sumMat = new int *[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
/ / making rooms for all entries in array
sumMat[row] = new int[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
/ / Then all the columns
for (int column = 0; column dimension; column++)
/ / Find the Boolean OR
sumMat[row][column] = firstMatrix[row][column] || secondMatrix[row][column];
/ * return the Boolean sum of two matrices of given dimension * /
return sumMat;
}
/ / Function definition
int **multiplyMatrixBoolean(int **firstMatrix, int **secondMatrix, int dimension)
{
/ * Used for multiplying two matrices of given dimension * /
int **productMat = new int *[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
/ / making rooms for all entries in array
productMat[row] = new int[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
/ / Then all the columns
for (int column = 0; column dimension; column++)
{
/ / Each time need to be set to zero
int sum = 0;
for (int k = 0; k dimension; k++)
{
/ / The Boolean OR, AND operation
sum |= firstMatrix[row][k] secondMatrix[k][column];
}
/ / The elements at the result matrix
productMat[row][column] = sum;
}
/ * The result of the multiplication of two matrices of given dimension * /
return productMat;
}
/ / Function definition
int **reachabilityMatrix(int **adjMat, int dimension)
{
/ * Used for finding the Boolean reachability matrix of given dimension for a graph represented by the given adjacency matrix; The dimension here is actually the count of vertices thus the dimension of reachability matrix is as same as adjacency matrix * /
int **reachMat = new int *[dimension];
/ / to create an identity matrix
int **idMat = new int *[dimension];
/ / For all the rows
for (int row = 0; row dimension; row++)
{
/ / making rooms for all entries in array
reachMat[row] = new int[dimension];
/ / making rooms for all entries in array
idMat[row] = new int[dimension];
/ / And creating an identity matrix
idMat[row][row] = 1;
}
/ / For all the vertices perform the following
for (int iterator = 0; iterator dimension; iterator++)
{
/ / addition of two matrices
reachMat = addMatrixBoolean(reachMat, idMat, dimension);
/ / multiplication of two matrices
idMat = multiplyMatrixBoolean(idMat, adjMat, dimension);
}
/ * The resultant matrix that represents the reachability matrix * /
return reachMat;
}
/ / Main function
int main()
{
/ / It holds the count of vertices in the graph
int countVertex;
/ / Prompt user for the count of vertices
cout "Enter the count of vertices: ";
/ / Holds the input for the count of vertices
cin countVertex;
/ *2-D matrices of dimension of count of vertices; represented by a pointer that will be passed on to functions* /
int **reachMatrix, **adjMatrix = new int *[countVertex];
/ / Initiate the adjacency matrix
for (int row = 0; row countVertex; row++)
/ * Making rooms for the entries in matrix by allocating space for an integer * /
adjMatrix[row] = new int[countVertex];
/ / Prompt to stdout for inputting the adjacency matrix
cout "Enter the adjacency matrix: " endl;
/ / For all the rows
for (int row = 0; row countVertex; row++)
/ / Then all the columns
for (int column = 0; column countVertex; column++)
/ *take input from the user to adjacency matrix * /
cin adjMatrix[row][column];
/ / Invoking the function for reachability matrix
reachMatrix = reachabilityMatrix(adjMatrix, countVertex);
/ / Notification for reachability matrix to stdout
cout "The corresponding reachability matrix: " endl;
/ / For all the rows
for (int row = 0; row countVertex; row++)
{
/ / Then all the columns
for (int column = 0; column countVertex; column++)
/ / Print the entry
cout reachMatrix[row][column] " ";
/ *At the end of a row, print a new line for a matrix like form * /
cout endl;
} / / End of for loop
return 0; / / For successful execution
} / / Ends here
Sample Output:
Enter the count of vertices: 5
Enter the adjacency matrix:
0 1 1 0 1
0 0 1 0 0
0 1 0 1 0
0 0 0 1 0
0 0 0 0 0
The corresponding reachability matrix:
1 1 1 1 1
0 1 1 1 0
0 1 1 1 0
0 0 0 1 0
0 0 0 0 1
4
Write a program to test the reachability-matrix function in Exercise 24 that implements Warshall's algorithm.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
5
Modify the class template Digraph in Figure 16.1 to use the adjacency-matrix representation for the digraph.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
6
Modify the class template Digraph in Figure 16.1 to use the linked adjacency-list representation described in the paragraph preceding Exercise 17 of Section 16.1.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
7
Write and test a function for the vertex-insertion algorithm in Exercise 33.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
8
Write and test a function for the search-and-retrieve algorithm in Exercise 34.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
9
Write and test a function for the vertex-deletion algorithm in Exercise 35.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
10
Write and test a function for the adjacent-vertices algorithm in Exercise 36.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
11
Write and test a function for the cycle-detection algorithm in Exercise 37.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
12
Write and test a function for the spanning-tree algorithm in Exercise 38.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
13
Write and test a function for Kruskal's spanning-tree algorithm in Exercise 39.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
14
Revise the Graph class template in Figure 16.4 so that it uses an adjacency-matrix representation for the graph.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
15
Proceed as in Problem 14, but use the adjacency-list representation.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
16
Proceed as in Problem 14, but use the linked adjacency-list representation described in Exercises 13-16.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
17
Write a program that reads and stores the names of persons and the names of job positions in the vertices of a graph. Two vertices will be connected if one of them represents a person and the other a job position for which that person is qualified. The program should allow the user to specify one of the following options:
a. Insert (a) a new applicant or (b) a new job position into the graph.
b. Delete (a) an applicant or (b) a job position from the graph.
c. List all persons qualified for a specified job position.
d. List all job positions for which a specified person is qualified.
Use the functions developed in Problems 7-10 to implement these operations.
a. Insert (a) a new applicant or (b) a new job position into the graph.
b. Delete (a) an applicant or (b) a job position from the graph.
c. List all persons qualified for a specified job position.
d. List all job positions for which a specified person is qualified.
Use the functions developed in Problems 7-10 to implement these operations.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
18
For Exercises 1-4, find the adjacency matrix adj and the data matrix data for the given digraph.
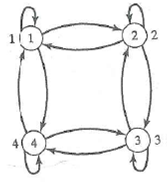


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
19
For Exercises 1-4, find the adjacency matrix adj and the data matrix data for the given digraph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
20
For Exercises 1-4, find the adjacency matrix adj and the data matrix data for the given digraph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
21
For Exercises 1-4, find the adjacency matrix adj and the data matrix data for the given digraph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
22
For Exercises 5-8, draw the directed graph represented by the given adjacency matrix adj and the data matrix data.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
23
For Exercises 5-8, draw the directed graph represented by the given adjacency matrix adj and the data matrix data.
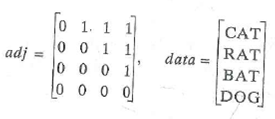


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
24
For Exercises 5-8, draw the directed graph represented by the given adjacency matrix adj and the data matrix data.
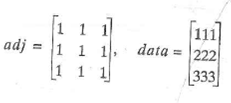
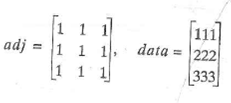

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
25
For Exercises 5-8, draw the directed graph represented by the given adjacency matrix adj and the data matrix data.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
26
Give the adjacency-list representation of the directed graphs in Exercises 1-4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
27
Give the adjacency-list representation of the directed graphs in Exercises 1-4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
28
Give the adjacency-list representation of the directed graphs in Exercises 1-4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
29
Give the adjacency-list representation of the directed graphs in Exercises 1-4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
30
Give the adjacency-list representation of the directed graphs in Exercises 5-8.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
31
Give the adjacency-list representation of the directed graphs in Exercises 5-8.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
32
Give the adjacency-list representation of the directed graphs in Exercises 5-8.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
33
Give the adjacency-list representation of the directed graphs in Exercises 5-8.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
34
An alternative to the adjacency-list representation for a directed graph is a linked adjacency-list representation that uses a linked list instead of an array or vector, one list node for each vertex in the digraph. A list node stores the data stored in a vertex together with a linked list of the numbers of all vertices adjacent to that vertex.
Give the linked adjacency-list representation of the directed graphs in Exercises 1-4.
Give the linked adjacency-list representation of the directed graphs in Exercises 1-4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
35
An alternative to the adjacency-list representation for a directed graph is a linked adjacency-list representation that uses a linked list instead of an array or vector, one list node for each vertex in the digraph. A list node stores the data stored in a vertex together with a linked list of the numbers of all vertices adjacent to that vertex.
Give the linked adjacency-list representation of the directed graphs in Exercises 1-4.
Give the linked adjacency-list representation of the directed graphs in Exercises 1-4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
36
An alternative to the adjacency-list representation for a directed graph is a linked adjacency-list representation that uses a linked list instead of an array or vector, one list node for each vertex in the digraph. A list node stores the data stored in a vertex together with a linked list of the numbers of all vertices adjacent to that vertex.
Give the linked adjacency-list representation of the directed graphs in Exercises 1-4.
Give the linked adjacency-list representation of the directed graphs in Exercises 1-4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
37
An alternative to the adjacency-list representation for a directed graph is a linked adjacency-list representation that uses a linked list instead of an array or vector, one list node for each vertex in the digraph. A list node stores the data stored in a vertex together with a linked list of the numbers of all vertices adjacent to that vertex.
Give the linked adjacency-list representation of the directed graphs in Exercises 1-4.
Give the linked adjacency-list representation of the directed graphs in Exercises 1-4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
38
An alternative to the adjacency-list representation for a directed graph is a linked adjacency-list representation that uses a linked list instead of an array or vector, one list node for each vertex in the digraph. A list node stores the data stored in a vertex together with a linked list of the numbers of all vertices adjacent to that vertex.
Give the linked adjacency-list representation of the directed graphs in Exercises 5-8.
Give the linked adjacency-list representation of the directed graphs in Exercises 5-8.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
39
An alternative to the adjacency-list representation for a directed graph is a linked adjacency-list representation that uses a linked list instead of an array or vector, one list node for each vertex in the digraph. A list node stores the data stored in a vertex together with a linked list of the numbers of all vertices adjacent to that vertex.
Give the linked adjacency-list representation of the directed graphs in Exercises 5-8.
Give the linked adjacency-list representation of the directed graphs in Exercises 5-8.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
40
An alternative to the adjacency-list representation for a directed graph is a linked adjacency-list representation that uses a linked list instead of an array or vector, one list node for each vertex in the digraph. A list node stores the data stored in a vertex together with a linked list of the numbers of all vertices adjacent to that vertex.
Give the linked adjacency-list representation of the directed graphs in Exercises 5-8.
Give the linked adjacency-list representation of the directed graphs in Exercises 5-8.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
41
An alternative to the adjacency-list representation for a directed graph is a linked adjacency-list representation that uses a linked list instead of an array or vector, one list node for each vertex in the digraph. A list node stores the data stored in a vertex together with a linked list of the numbers of all vertices adjacent to that vertex.
Give the linked adjacency-list representation of the directed graphs in Exercises 5-8.
Give the linked adjacency-list representation of the directed graphs in Exercises 5-8.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
42
In Exercises 25-30, draw the directed graph represented by the adjacency-list.
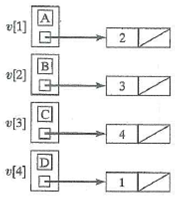


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
43
In Exercises 25-30, draw the directed graph represented by the adjacency-list.
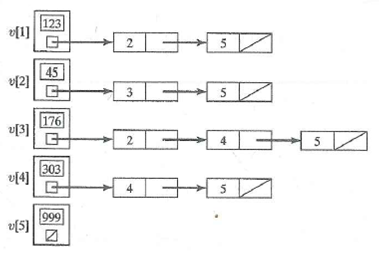


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
44
In Exercises 25-30, draw the directed graph represented by the adjacency-list.
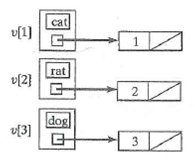


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
45
In Exercises 25-30, draw the directed graph represented by the adjacency-list.
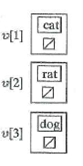


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
46
In Exercises 25-30, draw the directed graph represented by the adjacency-list.
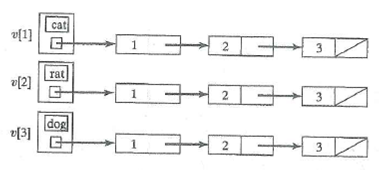


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
47
In Exercises 25-30, draw the directed graph represented by the adjacency-list.
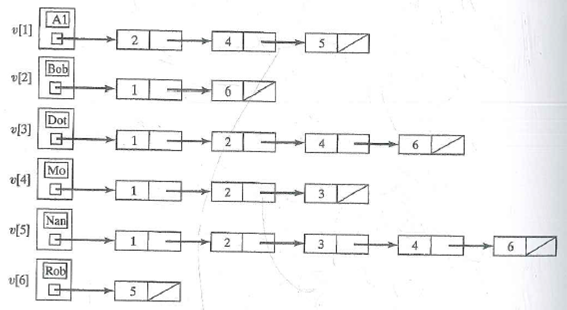


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
48
For Exercises 1-5, construct a trace table for the algorithm, using the digraph in Exercise 1 of Section 16.1. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex labeled with the smallest number.
Depth-first search starting at vertex 1.
Depth-first search starting at vertex 1.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
49
For Exercises 1-5, construct a trace table for the algorithm, using the digraph in Exercise 1 of Section 16.1. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex labeled with the smallest number.
Depth-first search starting at vertex 2.
Depth-first search starting at vertex 2.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
50
For Exercises 1-5, construct a trace table for the algorithm, using the digraph in Exercise 1 of Section 16.1. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex labeled with the smallest number.
Breadth-first search starting at vertex 1.
Breadth-first search starting at vertex 1.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
51
For Exercises 1-5, construct a trace table for the algorithm, using the digraph in Exercise 1 of Section 16.1. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex labeled with the smallest number.
Breadth-first search starting at vertex 2.
Breadth-first search starting at vertex 2.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
52
For Exercises 1-5, construct a trace table for the algorithm, using the digraph in Exercise 1 of Section 16.1. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex labeled with the smallest number.
Shortest path from vertex 2-to vertex 4.
Shortest path from vertex 2-to vertex 4.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
53
For Exercises 6-10, proceed as in Exercises 1-5, but use the digraph in Exercise 4 of Section 16.1.
Depth-first search starting at vertex 1.
Depth-first search starting at vertex 1.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
54
For Exercises 6-10, proceed as in Exercises 1-5, but use the digraph in Exercise 4 of Section 16.1.
Depth-first search starting at vertex 2.
Depth-first search starting at vertex 2.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
55
For Exercises 6-10, proceed as in Exercises 1-5, but use the digraph in Exercise 4 of Section 16.1.
Breadth-first search starting at vertex 1.
Breadth-first search starting at vertex 1.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
56
For Exercises 6-10, proceed as in Exercises 1-5, but use the digraph in Exercise 4 of Section 16.1.
Breadth-first search starting at vertex 2.
Breadth-first search starting at vertex 2.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
57
For Exercises 6-10, proceed as in Exercises 1-5, but use the digraph in Exercise 4 of Section 16.1.
Shortest path from vertex 4 to vertex 6.
Shortest path from vertex 4 to vertex 6.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
58
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
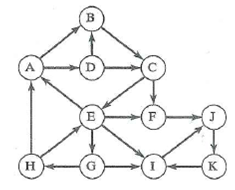
Depth-first search starting at vertex A.

Depth-first search starting at vertex A.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
59
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
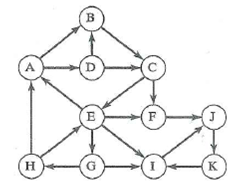
Depth-first search starting at vertex F.

Depth-first search starting at vertex F.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
60
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
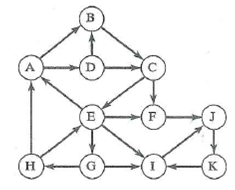
Breadth-first search starting at vertex A.

Breadth-first search starting at vertex A.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
61
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
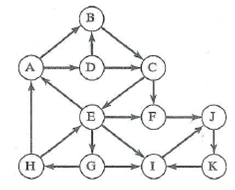
Breadth-first search starting at vertex F.

Breadth-first search starting at vertex F.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
62
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
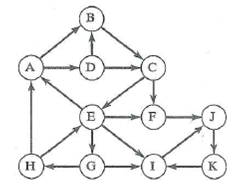
Shortest path from vertex A to vertex E.

Shortest path from vertex A to vertex E.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
63
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
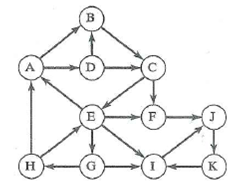
Shortest path from vertex A to vertex H.

Shortest path from vertex A to vertex H.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
64
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
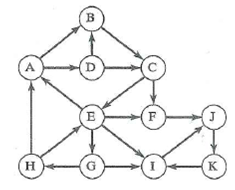
Shortest path from vertex G to vertex C.

Shortest path from vertex G to vertex C.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
65
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
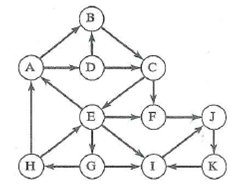
Shortest path from vertex J to vertex I.

Shortest path from vertex J to vertex I.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
66
For Exercises 11-19, proceed as in Exercises 1-5, but use the following digraph. Whenever a new vertex to visit must be selected and there is more than one possibility, use the vertex containing the letter that comes earliest in the alphabet.
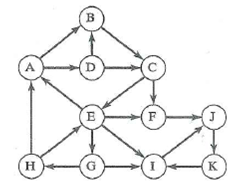
Shortest path from vertex J to vertex A.

Shortest path from vertex J to vertex A.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
67
The following exercises ask you to write functions. You should also write driver programs to test them, as instructed in Programming Problems 1-4 at the end of this chapter.
Add a function member to the Digraph class template for doing a breadth-first search from some start vertex.
Add a function member to the Digraph class template for doing a breadth-first search from some start vertex.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
68
The following exercises ask you to write functions. You should also write driver programs to test them, as instructed in Programming Problems 1-4 at the end of this chapter.
If A is an n × n adjacency matrix for a directed graph, then the entry in the i th row and j th column of A k is equal to the number of paths of length k from the i thvertex to the j th vertex in this digraph. The reachability matrix R of a digraph is the n × n matrix defined by
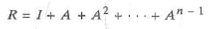
where I is the n × n identity matrix having ones on the diagonal (from upper left corner to lower right corner) and zeros off. In the digraph, there is a path from vertex i to vertex j if and only if the entry in row i and column j of R is nonzero. Write a function to find the reachability matrix for a directed graph.
If A is an n × n adjacency matrix for a directed graph, then the entry in the i th row and j th column of A k is equal to the number of paths of length k from the i thvertex to the j th vertex in this digraph. The reachability matrix R of a digraph is the n × n matrix defined by
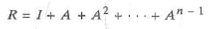
where I is the n × n identity matrix having ones on the diagonal (from upper left corner to lower right corner) and zeros off. In the digraph, there is a path from vertex i to vertex j if and only if the entry in row i and column j of R is nonzero. Write a function to find the reachability matrix for a directed graph.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
69
The following exercises ask you to write functions. You should also write driver programs to test them, as instructed in Programming Problems 1-4 at the end of this chapter.
An alternative to the method of Exercise 21 for determining reachability is to use "boolean multiplication and addition," that is, bitwise and ( ) and bitwise or (|) operations, in carrying out the matrix computations (0 = false , 1 = true ). Rewrite the function in Exercise 21 to find this form of the reachability matrix.
An alternative to the method of Exercise 21 for determining reachability is to use "boolean multiplication and addition," that is, bitwise and ( ) and bitwise or (|) operations, in carrying out the matrix computations (0 = false , 1 = true ). Rewrite the function in Exercise 21 to find this form of the reachability matrix.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
70
The following exercises ask you to write functions. You should also write driver programs to test them, as instructed in Programming Problems 1-4 at the end of this chapter.
Warshall's algorithm provides a more efficient method for calculating the boolean form of the reachability matrix described in Exercise 21:
a. Initialize R to A and k to 1.
b. While k ? n and R is not all ones do the following:
i. For i ranging from 1 to n with i ? k :
If the entry in the i th row and k th column of R is 1, then replace row i with (row i ) | (row k ).
ii. Increment k : by 1.
?End while.
Warshall's algorithm provides a more efficient method for calculating the boolean form of the reachability matrix described in Exercise 21:
a. Initialize R to A and k to 1.
b. While k ? n and R is not all ones do the following:
i. For i ranging from 1 to n with i ? k :
If the entry in the i th row and k th column of R is 1, then replace row i with (row i ) | (row k ).
ii. Increment k : by 1.
?End while.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
71
Use Warshall's algorithm to find the reachability matrix for the following digraph:
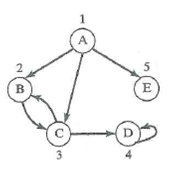
Write a function to find the reachability matrix of a digraph using Warshall's algorithm.

Write a function to find the reachability matrix of a digraph using Warshall's algorithm.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
72
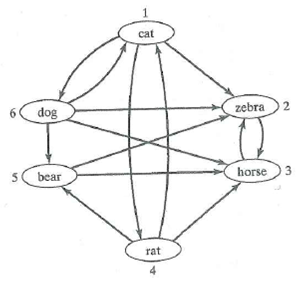
For Exercises 1-4, give the adjacency-matrix representation of the graph.
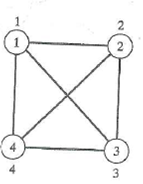


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
73
For Exercises 1-4, give the adjacency-matrix representation of the graph.
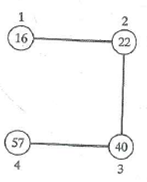


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
74
For Exercises 1-4, give the adjacency-matrix representation of the graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
75
For Exercises 1-4, give the adjacency-matrix representation of the graph.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
76
Proceed as in Exercises 1-4, but give the adjacency-list representation.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
77
Proceed as in Exercises 1-4, but give the adjacency-list representation.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
78
Proceed as in Exercises 1-4, but give the adjacency-list representation.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
79
Proceed as in Exercises 1-4, but give the adjacency-list representation.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
80
Proceed as in Exercises 1-4, but give the edge-list representation.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck



