Deck 10: Modeling Money
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/17
Play
Full screen (f)
Deck 10: Modeling Money
1
Suppose that the money-demand equation is :

Suppose initially that P = 1, Y = 7,000, and i = 5. If Y falls to 6,500 and the price level does not change, by how much should the Fed change the money supply if it wants to keep the nominal interest rate unchanged? Should the money supply rise or fall, and by how much? Use the liquidity-preference framework.

Suppose initially that P = 1, Y = 7,000, and i = 5. If Y falls to 6,500 and the price level does not change, by how much should the Fed change the money supply if it wants to keep the nominal interest rate unchanged? Should the money supply rise or fall, and by how much? Use the liquidity-preference framework.
Under the liquidity preference framework, the nominal interest rate (i) is determined at the point of intersection of money demand and money supply curves. It is shown in the figure below. It implies that the nominal rate of interest is that rate at which demand for money exactly equals the supply of money.
Money demand function is given by
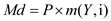 …… (1)
…… (1)
Where Md is the demand for money, Y is income and I is the nominal rate of interest.
In this problem it is given that the equation is
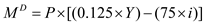 …… (2)
…… (2)
Here it is given that P = 1
Y = 7000
i = 5
Hence demand for money can be calculated using equation (2) as follows
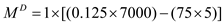
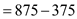
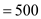 units
units
If Y falls to 6,500,


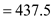 units
units
Thus if income (Y) falls to 6,500 from 7,000, the demand for money also falls to 437.5 units. That is a fall of 500 units in income causes a fall of 62.5 units in demand for money. Now if money supply remains the same the earlier equilibrium is disturbed. The nominal rate of interest must fall to make new demand for money equal the supply of money.
If the central bank wants to keep nominal rate of interest unchanged it must reduce money supply by exactly equal amount by which money demand has fallen. That is the central bank has to reduce money supply by 62.5 units.
Money demand function is given by
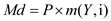 …… (1)
…… (1)Where Md is the demand for money, Y is income and I is the nominal rate of interest.
In this problem it is given that the equation is
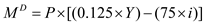 …… (2)
…… (2)Here it is given that P = 1
Y = 7000
i = 5
Hence demand for money can be calculated using equation (2) as follows
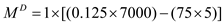
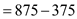
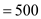 units
unitsIf Y falls to 6,500,


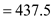 units
unitsThus if income (Y) falls to 6,500 from 7,000, the demand for money also falls to 437.5 units. That is a fall of 500 units in income causes a fall of 62.5 units in demand for money. Now if money supply remains the same the earlier equilibrium is disturbed. The nominal rate of interest must fall to make new demand for money equal the supply of money.
If the central bank wants to keep nominal rate of interest unchanged it must reduce money supply by exactly equal amount by which money demand has fallen. That is the central bank has to reduce money supply by 62.5 units.
2
In Equation , suppose that the coefficients
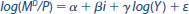
suppose that the coefficients are estimated as ? = 0, ? = -0.5, and ? = 1. If the nominal interest rate were to rise by 1 percentage point and income were to fall by 3 percent, by what percent would the quantity of real money demanded change? If prices were to fall 1 percent, by what percent would the quantity of nominal money demanded change?
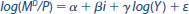
suppose that the coefficients are estimated as ? = 0, ? = -0.5, and ? = 1. If the nominal interest rate were to rise by 1 percentage point and income were to fall by 3 percent, by what percent would the quantity of real money demanded change? If prices were to fall 1 percent, by what percent would the quantity of nominal money demanded change?
 In the first case the calculation is as presented below-
In the first case the calculation is as presented below-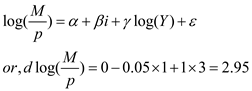 It implies that a change in real money demand is 2.95%.
It implies that a change in real money demand is 2.95%.Now in case prices also fall by 1% in that case also changes in nominal money demand remain 2.95%.
3
In the liquidity-preference framework, suppose that the Fed changes the money supply to keep the nominal interest rate unchanged whenever the demand for money shifts. Show what happens to the quantity of money and the nominal interest rate if the money-demand curve shifts to the right
Under the liquidity preference framework, the nominal interest rate (i) is determined at the point of intersection of money demand and money supply curves. It implies that the nominal rate of interest is that rate at which demand for money exactly equals the supply of money.
It is shown in the figure below. The equilibrium occurs at point 1 where money demand curve Md1 intersects money supply curve MS 1. The nominal rate of interest rate is r 1.
If for any reason money demand increases, the money demand curve shifts to the right and this equilibrium position is disturbed. The new equilibrium occurs at two, which is the point of intersection of the new money demand curve Md2 and the money supply curve MS 1. Money supply remaining the same, the nominal rate of interest will increase to r 2.
Thus, the equilibrium quantity of money remains the same since the money supply has not changed. Only the nominal rate of interest increases.
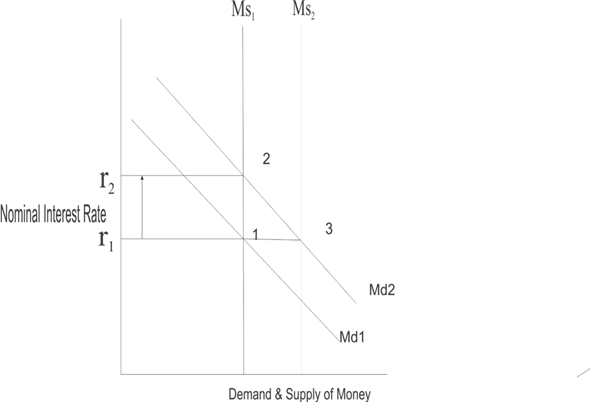 If the central bank wants to keep the nominal interest rate the same at r 1 , it should increase money supply to MS 2 (that is the amount equal to Md1-Md2). Then the equilibrium occurs at point 3 where MS2 and Md2 intersect.
If the central bank wants to keep the nominal interest rate the same at r 1 , it should increase money supply to MS 2 (that is the amount equal to Md1-Md2). Then the equilibrium occurs at point 3 where MS2 and Md2 intersect.
It is shown in the figure below. The equilibrium occurs at point 1 where money demand curve Md1 intersects money supply curve MS 1. The nominal rate of interest rate is r 1.
If for any reason money demand increases, the money demand curve shifts to the right and this equilibrium position is disturbed. The new equilibrium occurs at two, which is the point of intersection of the new money demand curve Md2 and the money supply curve MS 1. Money supply remaining the same, the nominal rate of interest will increase to r 2.
Thus, the equilibrium quantity of money remains the same since the money supply has not changed. Only the nominal rate of interest increases.
 If the central bank wants to keep the nominal interest rate the same at r 1 , it should increase money supply to MS 2 (that is the amount equal to Md1-Md2). Then the equilibrium occurs at point 3 where MS2 and Md2 intersect.
If the central bank wants to keep the nominal interest rate the same at r 1 , it should increase money supply to MS 2 (that is the amount equal to Md1-Md2). Then the equilibrium occurs at point 3 where MS2 and Md2 intersect. 4
Describe how a one-time decline in the money supply in a dynamic model affects the nominal interest rate over time

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
5
What is the difference between an exogenous variable and an endogenous variable?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose that the liquidity effect is small, people monitor changes in the money supply carefully, and prices and infl ation expectations adjust rapidly. In this situation, describe the movement of the nominal interest rate when there is a permanent decline in the growth rate of the money supply

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
7
Explain the difference between general-equilibrium models and partial-equilibrium models. How are the numbers of endogenous and exogenous variables related to whether a model is a partialequilibrium model or general-equilibrium model?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
8
What are the main factors that affect a person's decision about how often to go to an ATM?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
9
Describe the main factors at play in the liquiditypreference model. What variables does the model determine?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
10
What is the liquidity effect? Why does it occur in the liquidity-preference model?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
11
What is the main difference between a static model and a dynamic model?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
12
What is meant by the steady state in a dynamic model? Why is a steady state useful to analyze in a dynamic model?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
13
What is a shock in a dynamic model? What does a shock do in such a model?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
14
In U.S. data, how sensitive is the demand for money to changes in nominal interest rates?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
15
Is the demand-for-money function stable over time?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
16
Using a spreadsheet program or a calculator, solve Tracy's problem of how often to go to the ATM when the nominal interest rate on her bank account is 10 percent, she spends $30 each day, it costs her $0.50 each time she uses the ATM, and she thinks that there is a 15 percent chance that she will lose her cash or have it stolen. Under these conditions, how often does Tracy go to the ATM, and how much cash does she take out each time?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck
17
In the model of Tracy's decision about how often to go to the ATM in exercise 1, try to find a combination of parameters that would lead her to go to the ATM just once every 10 days. You can consider variations in Tracy's spending amount, her cost of using the ATM, the nominal interest rate, and the probability of having her cash lost or stolen. ( Hint: Use a spreadsheet program or use calculus.)
Exercise 1
Using a spreadsheet program or a calculator, solve Tracy's problem of how often to go to the ATM when the nominal interest rate on her bank account is 10 percent, she spends $30 each day, it costs her $0.50 each time she uses the ATM, and she thinks that there is a 15 percent chance that she will lose her cash or have it stolen. Under these conditions, how often does Tracy go to the ATM, and how much cash does she take out each time?
Exercise 1
Using a spreadsheet program or a calculator, solve Tracy's problem of how often to go to the ATM when the nominal interest rate on her bank account is 10 percent, she spends $30 each day, it costs her $0.50 each time she uses the ATM, and she thinks that there is a 15 percent chance that she will lose her cash or have it stolen. Under these conditions, how often does Tracy go to the ATM, and how much cash does she take out each time?

Unlock Deck
Unlock for access to all 17 flashcards in this deck.
Unlock Deck
k this deck



