Deck 5: A Closer Look at Instruction Set Architectures
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/64
Play
Full screen (f)
Deck 5: A Closer Look at Instruction Set Architectures
1
Fill in the following table to show how the given integers are represented, assuming that 16 bits are used to store values and the machine uses two's complement notation. 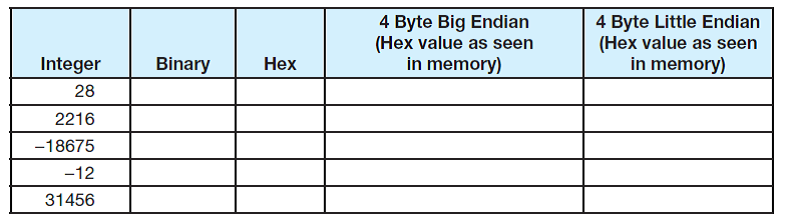

The term endian refers to a computer architecture's "byte order", or the way the computer stores the bytes of a multiple-byte data element.
• Big endian machines store information with the most significant byte first. Using big endian notation, the number is read from the higher order byte.
• Little endian machines store information with the least significant byte first. Using little endian notation, the number is read from the lower order byte.
BYTE ORDER
• Big endian machines store information with the most significant byte first. Using big endian notation, the number is read from the higher order byte.
• Little endian machines store information with the least significant byte first. Using little endian notation, the number is read from the lower order byte.
BYTE ORDER

2
How does an architecture based on zero operands ever get any data values from memory?
The use of a stack is necessary when machine instructions that do not allow for operands need to perform those that do. A stack-based architecture is preferred over the using general-purpose registers since it stores the operands on the top of a stack, which can be easily accessed by the CPU. The stack presents an efficient means of passing parameters during procedure calls. It also provides data storage capabilities, as well as the capacity to save local block structure and set variable and subroutine scope.
3
Convert the following expressions from reverse Polish notation to infix notation. 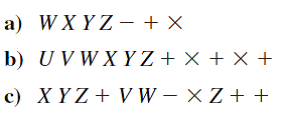
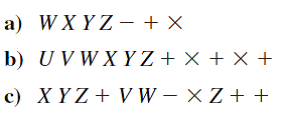
In order to convert a given reverser Polish (or Postfix) expression into the infix notation what we essentially do is start at the operators that are closest to the operands and then move the operator between the respective operands. In this case, precedence does not need to be separately considered as that aspect is also incorporated into the process.
a) W X Y Z - + In this case, the - operator is closest to the operands Y and Z and hence is accordingly moved between them:
In this case, the - operator is closest to the operands Y and Z and hence is accordingly moved between them:
W X (Y-Z) + Now we see that the + sign operates on the result of (Y-Z) and next operand, X:
Now we see that the + sign operates on the result of (Y-Z) and next operand, X:
W (X + (Y-Z)) Finally, the multiplication sign is moved to reflect the complete infix expression:
Finally, the multiplication sign is moved to reflect the complete infix expression:
W (X + (Y-Z))
(X + (Y-Z))
b) U V W X Y Z + +
+  +
+
In this case, the + operator is closest to the operands Y and Z and hence is accordingly moved between them:
U V W X (Y+Z) +
+  +
+
Now we see that the sign operates on the result of (Y+Z) and next operand, X:
sign operates on the result of (Y+Z) and next operand, X:
U V W (X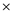 (Y+Z)) +
(Y+Z)) + 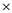 +
+
Similarly, the + sign operates on the result of (X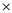 (Y+Z)) and next operand, W:
(Y+Z)) and next operand, W:
U V (W + (X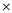 (Y+Z)))
(Y+Z)))  +
+
Similarly, first the sign and then the + sign are moved to operate on the operands as follows:
sign and then the + sign are moved to operate on the operands as follows:
(U+ (V (W + (X
(W + (X  (Y+Z)))))
(Y+Z)))))
c) X Y Z + V W -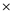 Z + +
Z + +
In this case, the + operator is closest to the operands Y and Z and similarly, - is closest to V and W and are hence moved accordingly between the operands:
X (Y+Z) (V-W)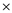 Z + +
Z + +
Next for evaluation is the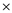 operator, which is closest to the result of (Y+Z) and (V-W) and hence is accordingly moved between them:
operator, which is closest to the result of (Y+Z) and (V-W) and hence is accordingly moved between them:
X ((Y+Z)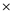 (V-W)) Z + +
(V-W)) Z + +
Next to be evaluated are the two + operators, which, are accordingly repositioned based on their proximity to the operands:
X + (((Y+Z) (V-W)) + Z)
(V-W)) + Z)
a) W X Y Z - +
 In this case, the - operator is closest to the operands Y and Z and hence is accordingly moved between them:
In this case, the - operator is closest to the operands Y and Z and hence is accordingly moved between them:W X (Y-Z) +
 Now we see that the + sign operates on the result of (Y-Z) and next operand, X:
Now we see that the + sign operates on the result of (Y-Z) and next operand, X:W (X + (Y-Z))
 Finally, the multiplication sign is moved to reflect the complete infix expression:
Finally, the multiplication sign is moved to reflect the complete infix expression:W
 (X + (Y-Z))
(X + (Y-Z)) b) U V W X Y Z +
 +
+  +
+ In this case, the + operator is closest to the operands Y and Z and hence is accordingly moved between them:
U V W X (Y+Z)
 +
+  +
+Now we see that the
 sign operates on the result of (Y+Z) and next operand, X:
sign operates on the result of (Y+Z) and next operand, X:U V W (X
 (Y+Z)) +
(Y+Z)) +  +
+Similarly, the + sign operates on the result of (X
 (Y+Z)) and next operand, W:
(Y+Z)) and next operand, W:U V (W + (X
 (Y+Z)))
(Y+Z)))  +
+Similarly, first the
 sign and then the + sign are moved to operate on the operands as follows:
sign and then the + sign are moved to operate on the operands as follows:(U+ (V
 (W + (X
(W + (X  (Y+Z)))))
(Y+Z))))) c) X Y Z + V W -
 Z + +
Z + + In this case, the + operator is closest to the operands Y and Z and similarly, - is closest to V and W and are hence moved accordingly between the operands:
X (Y+Z) (V-W)
 Z + +
Z + +Next for evaluation is the
 operator, which is closest to the result of (Y+Z) and (V-W) and hence is accordingly moved between them:
operator, which is closest to the result of (Y+Z) and (V-W) and hence is accordingly moved between them:X ((Y+Z)
 (V-W)) Z + +
(V-W)) Z + +Next to be evaluated are the two + operators, which, are accordingly repositioned based on their proximity to the operands:
X + (((Y+Z)
 (V-W)) + Z)
(V-W)) + Z) 4
A nonpipelined system takes 200ns to process a task. The same task can be processed in a five-segment pipeline with a clock cycle of 40ns. Determine the speedup ratio of the pipeline for 200 tasks. What is the maximum speedup that could be achieved with the pipeline unit over the nonpipelined unit?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
5
What is an expanding opcode?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
6
Expanding opcodes make instruction decoding much easier than when it is not used.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
7
What is an address mode?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
8
List several ways in which the Intel and MIPS ISAs differ. Name several ways in which they are the same.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
9
An instruction takes less time to execute on a processor using an instruction pipeline than on a processor without an instruction pipeline.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
10
There are reasons for machine designers to want all instructions to be the same length. Why is this not a good idea on a stack machine?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
11
Explain how a stack is used to evaluate the RPN expressions from exercise 13.
Reference of Exercise 13:
Convert the following expressions from reverse Polish notation to infix notation.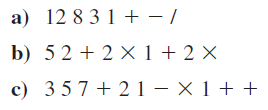
Reference of Exercise 13:
Convert the following expressions from reverse Polish notation to infix notation.
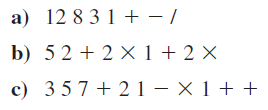

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
12
A nonpipelined system takes 100ns to process a task. The same task can be processed in a five-stage pipeline with a clock cycle of 20ns. Determine the speedup ratio of the pipeline for 100 tasks. What is the theoretical speedup that could be achieved with the pipeline system over a nonpipelined system?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
13
Assume a computer that has 32-bit integers. Show how each of the following values would be stored sequentially in memory, starting at address 0x100, assuming that each address holds 1 byte. Be sure to extend each value to the appropriate number of bits. You will need to add more rows (addresses) to store all given values. 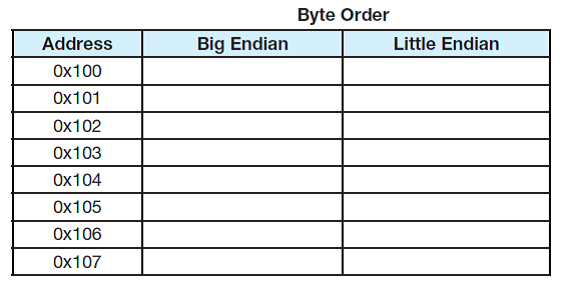
a) 0xAB123456
b) 0x2BF876
c) 0x8B0A1
d) 0x1
e) 0xFEDC1234

a) 0xAB123456
b) 0x2BF876
c) 0x8B0A1
d) 0x1
e) 0xFEDC1234

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
14
Which is likely to be longer (have more instructions): a program written for a zero address architecture, a program written for a one-address architecture, or a program written for a two-address architecture? Why?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
15
Give examples of immediate, direct, register, indirect, register indirect, and indexed addressing.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
16
Explain Java bytecodes.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
17
If a byte-addressable machine with 32-bit words stores the hex value 98765432, indicate how this value would be stored on a little endian machine and on a big endian machine. Why does "endian-ness" matter?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
18
Instruction set orthogonality refers to the characteristic in an instruction set architecture where each instruction has a "backup" instruction that performs the same operation.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
19
Write the following expression in postfix (reverse Polish) notation. Remember the rules of precedence for arithmetic operators! 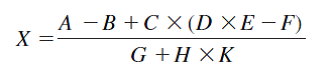
b) Write a program to evaluate the above arithmetic statement using a stack-organized computer with zero-address instructions (so only Pop and Push can access memory).
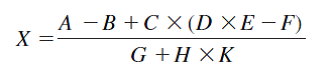
b) Write a program to evaluate the above arithmetic statement using a stack-organized computer with zero-address instructions (so only Pop and Push can access memory).

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
20
Assuming the same stages as in Example 5.12, explain the potential pipeline hazards (if any) in each of the following code segments. 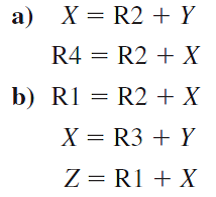
Reference of Example 5.12:
Suppose we have a 4-stage pipeline, where:
• S1 = fetch instruction
• S2 = decode and calculate effective address
• S3 = fetch operand
• S4 = execute instruction and store results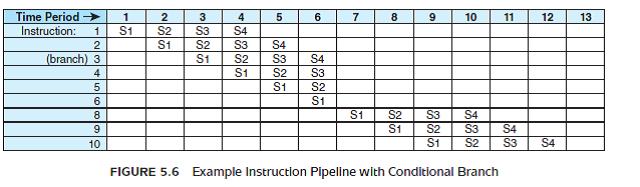
We must also assume that the architecture provides a means to fetch data and instructions in parallel. This can be done with separate instruction and data paths; however, most memory systems do not allow this. Instead, they provide the operand in cache, which, in most cases, allows the instruction and operand to be fetched simultaneously. Suppose, also, that instruction I3 is a conditional branch statement that alters the execution sequence (so that instead of I4 running next, it transfers control to I8). This results in the pipeline operation shown in Figure 5.6.
Note that I4, I5, and I6 are fetched and proceed through various stages, but after the execution of I3 (the branch), I4, I5, and I6 are no longer needed. Only after time period 6, when the branch has executed, can the next instruction to be executed (I8) be fetched, after which the pipe refills. From time periods 6 through 9, only one instruction has executed. In a perfect world, for each time period after the pipe originally fills, one instruction should flow out of the pipeline. However, we see in this example that this is not necessarily true.
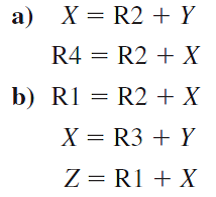
Reference of Example 5.12:
Suppose we have a 4-stage pipeline, where:
• S1 = fetch instruction
• S2 = decode and calculate effective address
• S3 = fetch operand
• S4 = execute instruction and store results

We must also assume that the architecture provides a means to fetch data and instructions in parallel. This can be done with separate instruction and data paths; however, most memory systems do not allow this. Instead, they provide the operand in cache, which, in most cases, allows the instruction and operand to be fetched simultaneously. Suppose, also, that instruction I3 is a conditional branch statement that alters the execution sequence (so that instead of I4 running next, it transfers control to I8). This results in the pipeline operation shown in Figure 5.6.
Note that I4, I5, and I6 are fetched and proceed through various stages, but after the execution of I3 (the branch), I4, I5, and I6 are no longer needed. Only after time period 6, when the branch has executed, can the next instruction to be executed (I8) be fetched, after which the pipe refills. From time periods 6 through 9, only one instruction has executed. In a perfect world, for each time period after the pipe originally fills, one instruction should flow out of the pipeline. However, we see in this example that this is not necessarily true.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
21
The term "endian" refers to an architecture's byte ordering.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
22
A computer has 32-bit instructions and 12-bit addresses. Suppose there are 250 two address instructions. How many one-address instructions can be formulated? Explain your answer.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
23
How does indexed addressing differ from based addressing?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
24
Give an example of a current stack-based architecture and a current GPR-based architecture. How do they differ?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
25
Consider a 32-bit hexadecimal number stored in memory as follows: 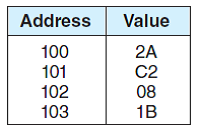
a) If the machine is big endian and uses two's complement representation for integers, write the 32-bit integer number stored at address 100 (you may write the number in hex).
b) If the machine is big endian and the number is an IEEE single-precision floating point value, is the number positive or negative?
c) If the machine is big endian and the number is an IEEE single-precision floating-point value, determine the decimal equivalent of the number stored at address 100 (you may leave your answer in scientific notation form, as a number times a power of two).
d) If the machine is little endian and uses two's complement representation for integers, write the 32-bit integer number stored at address 100 (you may write the number in hex).
e) If the machine is little endian and the number is an IEEE single-precision floating point value, is the number positive or negative?
f) If the machine is little endian and the number is an IEEE single-precision floating point value, determine the decimal equivalent of the number stored at address 100 (you may leave your answer in scientific notation form, as a number times a power of two).

a) If the machine is big endian and uses two's complement representation for integers, write the 32-bit integer number stored at address 100 (you may write the number in hex).
b) If the machine is big endian and the number is an IEEE single-precision floating point value, is the number positive or negative?
c) If the machine is big endian and the number is an IEEE single-precision floating-point value, determine the decimal equivalent of the number stored at address 100 (you may leave your answer in scientific notation form, as a number times a power of two).
d) If the machine is little endian and uses two's complement representation for integers, write the 32-bit integer number stored at address 100 (you may write the number in hex).
e) If the machine is little endian and the number is an IEEE single-precision floating point value, is the number positive or negative?
f) If the machine is little endian and the number is an IEEE single-precision floating point value, determine the decimal equivalent of the number stored at address 100 (you may leave your answer in scientific notation form, as a number times a power of two).

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
26
Why might stack architectures represent arithmetic expressions in reverse Polish notation?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
27
In a computer instruction format, the instruction length is 11 bits and the size of an address field is 4 bits. Is it possible to have
5 two-address instructions
45 one-address instructions
32 zero-address instructions
using the specified format? Justify your answer.
b) Assume that a computer architect has already designed 6 two-address and 24 zeroaddress instructions using the instruction format above. What is the maximum number of one-address instructions that can be added to the instruction set?
5 two-address instructions
45 one-address instructions
32 zero-address instructions
using the specified format? Justify your answer.
b) Assume that a computer architect has already designed 6 two-address and 24 zeroaddress instructions using the instruction format above. What is the maximum number of one-address instructions that can be added to the instruction set?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
28
Write code to implement the expression A = ( B + C ) × ( D + E ) on three-, two-, one-, and zero-address machines. In accordance with programming language practice, computing the expression should not change the values of its operands.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
29
We can design stack architectures, accumulator architectures, or general-purpose register architectures. Explain the differences between these choices and give some situations where one might be better than another.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
30
The effective address of an operand is the value of its actual address in memory.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
31
Why do we need so many different addressing modes?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
32
A digital computer has a memory unit with 24 bits per word. The instruction set consists of 150 different operations. All instructions have an operation code part (opcode) and an address part (allowing for only one address). Each instruction is stored in one word of memory.
a) How many bits are needed for the opcode?
b) How many bits are left for the address part of the instruction?
c) What is the maximum allowable size for memory?
d) What is the largest unsigned binary number that can be accommodated in one word of memory?
a) How many bits are needed for the opcode?
b) How many bits are left for the address part of the instruction?
c) What is the maximum allowable size for memory?
d) What is the largest unsigned binary number that can be accommodated in one word of memory?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
33
Stack architectures have good code density and a simple model for evaluation of expressions, but do not allow random access, which can cause a problem with the generation of efficient code.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
34
Convert the following expressions from infix to reverse Polish (postfix) notation. 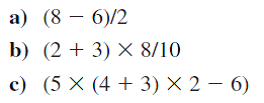
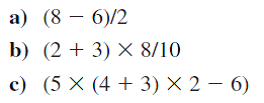

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose a computer has an instruction format with space for an opcode and either three register values or one register value and an address. What are the various instruction formats that could be used for an ADD instruction on this machine?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
36
The memory unit of a computer has 256K words of 32 bits each. The computer has an instruction format with four fields: an opcode field; a mode field to specify one of seven addressing modes; a register address field to specify one of 60 registers; and a memory address field. Assume an instruction is 32 bits long. Answer the following:
a) How large must the mode field be?
b) How large must the register field be?
c) How large must the address field be?
d) How large is the opcode field?
a) How large must the mode field be?
b) How large must the register field be?
c) How large must the address field be?
d) How large is the opcode field?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
37
The first two bytes of a 2M × 16 main memory have the following hex values:
• Byte 0 is FE
• Byte 1 is 01
If these bytes hold a 16-bit two's complement integer, what is its actual decimal value if:
a) memory is big endian?
b) memory is little endian?
• Byte 0 is FE
• Byte 1 is 01
If these bytes hold a 16-bit two's complement integer, what is its actual decimal value if:
a) memory is big endian?
b) memory is little endian?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
38
Name the seven types of data instructions and explain each.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
39
Explain the concept behind instruction pipelining.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose an instruction takes four cycles to execute in a nonpipelined CPU: one cycle to fetch the instruction, one cycle to decode the instruction, one cycle to perform the ALU operation, and one cycle to store the result. In a CPU with a four-stage pipeline, that instruction still takes four cycles to execute, so how can we say the pipeline speeds up the execution of the program?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
41
Assume you have a byte-addressable machine that uses 32-bit integers and you are storing the hex value 1234 at address 0:
a) Show how this is stored on a big endian machine.
b) Show how this is stored on a little endian machine.
c) If you wanted to increase the hex value to 123456, which byte assignment would be more efficient, big or little endian? Explain your answer.
a) Show how this is stored on a big endian machine.
b) Show how this is stored on a little endian machine.
c) If you wanted to increase the hex value to 123456, which byte assignment would be more efficient, big or little endian? Explain your answer.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
42
How do memory-memory, register-memory, and load-store architectures differ? How are they the same?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
43
Resource conflicts occur in a pipeline when there are multiple instructions that require the same resource.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
44
Given 16-bit instructions, is it possible to use expanding opcodes to allow the following to be encoded assuming we have a total of 32 registers? If so, show the encoding. If not, explain why is it not possible.
• 60 instructions with two register operands
• 30 instructions with one register operand
• 3 instructions with one 10-bit address
• 26 instructions with zero operands
• 60 instructions with two register operands
• 30 instructions with one register operand
• 3 instructions with one 10-bit address
• 26 instructions with zero operands

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
45
Explain the difference between register-to-register, register-to-memory, and memory-to- memory instructions.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
46
Most architectures today are accumulator based.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
47
Convert the following expressions from infix to reverse Polish (postfix) notation. 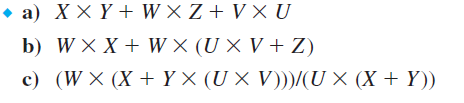
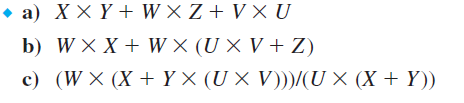

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
48
What is the theoretical speedup for a 4-stage pipeline with a 20ns clock cycle if it is processing 100 tasks?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
49
Most computers typically fall into one of three types of CPU organization: (1) general register organization; (2) single accumulator organization; or (3) stack organization.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
50
What kinds of problems do you think endian-ness can cause if you wished to transfer data from a big endian machine to a little endian machine? Explain.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
51
What is the difference between an arithmetic shift and a logical shift?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
52
What is the difference between using direct and indirect addressing? Give an example.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
53
Show how the following values would be stored by byte-addressable machines with 32-bit words, using little endian and then big endian format. Assume that each value starts at address 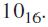 Draw a diagram of memory for each, placing the appropriate values in the correct (and labeled) memory locations.
Draw a diagram of memory for each, placing the appropriate values in the correct (and labeled) memory locations.
a) 0x456789A1
b) 0x0000058A
c) 0x14148888
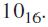 Draw a diagram of memory for each, placing the appropriate values in the correct (and labeled) memory locations.
Draw a diagram of memory for each, placing the appropriate values in the correct (and labeled) memory locations.a) 0x456789A1
b) 0x0000058A
c) 0x14148888

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
54
What are the pros and cons of fixed-length and variable-length instructions? Which is currently more popular?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
55
Data dependencies occur in a pipeline when multiple instructions need the CPU.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
56
What are the pipeline conflicts that can cause a slowdown in the pipeline?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
57
Several design decisions exist with regard to instruction sets. Name four and explain.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
58
Fixed-length instruction format typically results in better performance than variablelength instruction format.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
59
Convert the following expressions from reverse Polish notation to infix notation. 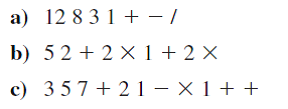
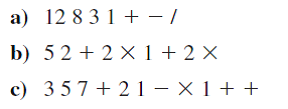

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
60
What are the two types of ILP, and how do they differ?

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
61
The advantage of zero-address instruction computers is that they have short programs; the disadvantage is that the instructions require many bits, making them very long.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
62
The Population Studies Institute monitors the population of the United States. In 2008, this institute wrote a program to create files of the numbers representing populations of the various states, as well as the total population of the United States. This program, which runs on a Motorola processor, projects the population based on various rules, such as the average numbers of births and deaths per year. The institute runs the program and then ships the output files to state agencies so the data values can be used as input into various applications. However, one Pennsylvania agency, running all Intel machines, encountered difficulties, as indicated by the following problem. When the 32-bit unsigned integer 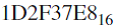 (representing the overall U.S. population prediction for 2013) is used as input, and the agency's program simply outputs this input value, the U.S. population forecast for 2014 is far too large. Can you help this Pennsylvania agency by explaining what might be going wrong? (Hint: They are run on different processors.)
(representing the overall U.S. population prediction for 2013) is used as input, and the agency's program simply outputs this input value, the U.S. population forecast for 2014 is far too large. Can you help this Pennsylvania agency by explaining what might be going wrong? (Hint: They are run on different processors.)
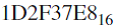 (representing the overall U.S. population prediction for 2013) is used as input, and the agency's program simply outputs this input value, the U.S. population forecast for 2014 is far too large. Can you help this Pennsylvania agency by explaining what might be going wrong? (Hint: They are run on different processors.)
(representing the overall U.S. population prediction for 2013) is used as input, and the agency's program simply outputs this input value, the U.S. population forecast for 2014 is far too large. Can you help this Pennsylvania agency by explaining what might be going wrong? (Hint: They are run on different processors.)
Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
63
Explain what it means for an instruction set to be orthogonal.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
64
Explain superscalar, superpipelining, and VLIW architectures.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck



