Deck 5: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/54
Play
Full screen (f)
Deck 5: Probability
1
S = {E1, E2, E3, E4, E5, E6}.A = {E1, E4}.What is A′?
A) {E1, E2, E3, E4, E5, E6}
B) {E1, E3, E4, E5, E6}
C) {E2, E3, E5}
D) {E2, E3, E5, E6}
A) {E1, E2, E3, E4, E5, E6}
B) {E1, E3, E4, E5, E6}
C) {E2, E3, E5}
D) {E2, E3, E5, E6}
{E2, E3, E5, E6}
2
For any two events A and B, if A∩B = { } (where { } is defined as the empty set), then A and B are said to be:
A) uncommon events.
B) unified events.
C) disjoint events.
D) disheveled events.
A) uncommon events.
B) unified events.
C) disjoint events.
D) disheveled events.
disjoint events.
3
For any two events denoted A and B, the event A∩B is best described as:
A) all outcomes in A or B or both.
B) all outcomes in both A and B.
C) all outcomes that are in neither A nor B.
D) all outcomes that are in A and not in B.
A) all outcomes in A or B or both.
B) all outcomes in both A and B.
C) all outcomes that are in neither A nor B.
D) all outcomes that are in A and not in B.
all outcomes in both A and B.
4
Sixty-five percent of the students who take introductory statistics start the semester with a poor opinion of statistics.If a randomly selected introductory statistics student has a poor opinion of statistics at the beginning of the semester, what is the probability that the person has had some negative experience with a previous math class?
A) 0.5844
B) 0.5005
C) 0.6923
D) 0.2925
A) 0.5844
B) 0.5005
C) 0.6923
D) 0.2925

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose we have a group of 5 children and wish to randomly select 2 from the group without replacement.How many possible unique samples of size 2 are possible if the order of selection does not matter?
A) 2
B) 5
C) 20
D) 10
A) 2
B) 5
C) 20
D) 10

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
6
A recent demographic study conducted in the U.S.South classified all surveyed participants into one of only five possible religious categories: Roman Catholic, Protestant, Islamic, Jewish, Other.The table summarizes the survey results. 
Find P(Roman Catholic′).
A) 0.13
B) 0.31
C) 0.57
D) 0.87

Find P(Roman Catholic′).
A) 0.13
B) 0.31
C) 0.57
D) 0.87

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose you roll a pair of dice.What is the probability that you roll the two dice so that they add up to 7 or 11?
A) 2/6
B) 4/36
C) 8/36
D) 9/36
A) 2/6
B) 4/36
C) 8/36
D) 9/36

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following is equal to 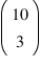 ?
?
A)
B) 10!
C) 10! / 3!
D) 210
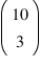 ?
?A)

B) 10!
C) 10! / 3!
D) 210

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
9
A tree diagram is:
A) similar to a Venn diagram and useful for visually depicting a data set.
B) a useful tool for graphically depicting a sample space.
C) vital for choosing the experimental outcome that is certain to occur in the next trial.
D) the only way to determine accurate probability estimates.
A) similar to a Venn diagram and useful for visually depicting a data set.
B) a useful tool for graphically depicting a sample space.
C) vital for choosing the experimental outcome that is certain to occur in the next trial.
D) the only way to determine accurate probability estimates.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
10
0! =
A) 1.
B) 0.
C) 2.
D) undefined.
A) 1.
B) 0.
C) 2.
D) undefined.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
11
Three factory workers work independently assembling office chairs for a local furniture wholesaler.Each worker completely assembles one chair per day.Worker number 1 has a defect rate of 0.01, worker number 2 has a defect rate of 0.15, and worker number 3 has a defect rate of 0.19 (workers 2 and 3 are very poor workers).What is the probability that on any given day, the workers produce three defective chairs?
A) 2.85 × 10-4
B) 0.35
C) 2.315 × 10-11
D) 0.2%
A) 2.85 × 10-4
B) 0.35
C) 2.315 × 10-11
D) 0.2%

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
12
How many two-digit numbers are there, with both digits odd?
A) 10
B) 25
C) 45
D) 90
A) 10
B) 25
C) 45
D) 90

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
13
If { } is defined as the empty set, then by definition P({ }) must be:
A) greater than 0.
B) equal to 0.
C) less than 0.
D) between 0 and 1, exclusive.
A) greater than 0.
B) equal to 0.
C) less than 0.
D) between 0 and 1, exclusive.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
14
If the outcome of one event has no bearing on the probability of another, the two events are said to be:
A) disjoint.
B) mutually exclusive.
C) independent.
D) conditional.
A) disjoint.
B) mutually exclusive.
C) independent.
D) conditional.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
15
Steve has 18 black socks and 12 blue socks.Every morning he pulls a sock at random from his drawer, then pulls a second sock at random, and wears both socks, regardless of their color.What is the probability he wears mismatched socks?
A) 0.248
B) 0.152
C) 0.352
D) 0.50
A) 0.248
B) 0.152
C) 0.352
D) 0.50

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
16
Suppose a population contains 1,000,000 people, 5000 of whom have a disease.The table shows the number of people who have the disease and test positive, etc. 
Based on the table, what is the probability that a person who tests positive actually has the disease?
A) 97.7%
B) 92.6%
C) 6.2%
D) 7.4%

Based on the table, what is the probability that a person who tests positive actually has the disease?
A) 97.7%
B) 92.6%
C) 6.2%
D) 7.4%

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
17
The California Lottery's Super Lotto Plus game involves picking five numbers between 1 and 47.There are 1,533,939 different ways that five numbers could be picked, and 571,341 different ways to pick at least one pair of consecutive numbers in this lottery game.What is the probability a person playing this game picks at least one pair of consecutive numbers?
A) 0.3725
B) 2.684564
C) 0.0213
D) 0.47
A) 0.3725
B) 2.684564
C) 0.0213
D) 0.47

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
18
An experiment consists of three tosses of a two-sided coin with the possible outcomes heads (H) or tails (T) from each toss.The outcome space is:
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
We define event A as "no heads are observed" and event B as "no tails are observed." What is AUB?
A) { } (the empty set)
B) {HHH}
C) {TTT, HHH}
D) {TTT}
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
We define event A as "no heads are observed" and event B as "no tails are observed." What is AUB?
A) { } (the empty set)
B) {HHH}
C) {TTT, HHH}
D) {TTT}

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
19
A wildlife biology crew is tagging deer in California for a census.If, on a statewide basis, 40% of deer are males (bucks), what is the probability that the crew will randomly and independently tag three females (does) in a row, assuming the area's deer population is representative of the entire state? (Assume an infinite population.)
A) 0.216
B) 1.2
C) 0.064
D) 0.180
A) 0.216
B) 1.2
C) 0.064
D) 0.180

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
20
The current form of the Milton Bradley board game Life includes a circular spinner that has 10 evenly spaced numbers around the edge, which specify the number of places a character will move.Assuming the spinner is balanced, the outcomes 1 through 10 inclusive are equally likely.On your next turn, you must move more than 4 spaces to be in the lead.However, in your current location on the game board, every other space (each odd space) gives you an undesirable result.What is the probability that on your next turn you will be in the lead and not have an undesirable result?
A) 0.2
B) 0.4
C) 0.3
D) 0.6
A) 0.2
B) 0.4
C) 0.3
D) 0.6

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following statements is true if and only if events A and B are independent?
A) P(A∪B) = P(A) + P(B)
B) P(A∩B) = P(A) ∙ P(B)
C) P(A∩B) = P(A) ∙ P
D)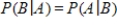
A) P(A∪B) = P(A) + P(B)
B) P(A∩B) = P(A) ∙ P(B)
C) P(A∩B) = P(A) ∙ P
D)
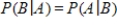

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
22
If a series of n events are known to be independent, the probability of the entire series of events occurring is:
A) the sum of the individual event probabilities minus the intersection probability.
B) the product of the individual event probabilities.
C) always 1.
D) never 0.
A) the sum of the individual event probabilities minus the intersection probability.
B) the product of the individual event probabilities.
C) always 1.
D) never 0.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
23
On a given day, 280 people jaywalk across a busy intersection.Of these people, 50% are male, 80% are university undergraduate students, and 40% are female university undergraduate students.A person is hit by a car while jaywalking across the intersection.We can see that the person is female.What is the probability that the victim is a university undergraduate student?
A) 0.40
B) 0.32
C) 0.10
D) 0.80
A) 0.40
B) 0.32
C) 0.10
D) 0.80

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
24
A recent demographic study conducted in the U.S.South classified all surveyed participants into one of only five possible religious categories: Roman Catholic, Protestant, Islamic, Jewish, Other.The table summarizes the survey results. 
If the researchers designate Roman Catholic as R and Protestant as event Pr, what is P(RUPr)?
A) 0.51
B) 0.06
C) 0.69
D) 0.57

If the researchers designate Roman Catholic as R and Protestant as event Pr, what is P(RUPr)?
A) 0.51
B) 0.06
C) 0.69
D) 0.57

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
25
The table shows the results of an experiment used to test whether Red Dye #2 causes cancer in laboratory rats. 
Based on the table, what is the probability that a rat that was given a high dose of the dye did not have a tumor?
A) 0.13
B) 0.30
C) 0.70
D) 0.43

Based on the table, what is the probability that a rat that was given a high dose of the dye did not have a tumor?
A) 0.13
B) 0.30
C) 0.70
D) 0.43

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose that an ice cream shop offers a special deal one day: The price of a small ice cream cone will be determined by rolling a pair of ordinary, six-sided dice.The price (in cents) will be the larger number followed by the smaller number.Let A be the event that the price of a cone costs more than 50 cents.What is the complementary event?
A) The price of an ice cream cone does not cost 50 cents.
B) The price of an ice cream cone costs less than 50 cents.
C) The price of an ice cream cone costs no more than 50 cents.
D) The price of an ice cream cone costs at least 50 cents.
A) The price of an ice cream cone does not cost 50 cents.
B) The price of an ice cream cone costs less than 50 cents.
C) The price of an ice cream cone costs no more than 50 cents.
D) The price of an ice cream cone costs at least 50 cents.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
27
If P(A) = 1, then we know that event A is:
A) highly unlikely to occur.
B) almost certain to occur.
C) absolutely certain to occur.
D) absolutely certain not to occur.
A) highly unlikely to occur.
B) almost certain to occur.
C) absolutely certain to occur.
D) absolutely certain not to occur.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
28
The sum of the probabilities of all possible outcomes in a sample space is:
A) always 0.
B) always between 0 and 1.
C) always 1.
D) always more than1.
A) always 0.
B) always between 0 and 1.
C) always 1.
D) always more than1.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
29
Which of the following statements is true in general (i.e., always true for all situations)?
A) P(A∪B)= P(A) + P(B)
B) P(A∩B) = P(A) · P(B)
C) P(B∩A) = P(A) · P(B|A)
D) P(B|A) = P(A|B)
A) P(A∪B)= P(A) + P(B)
B) P(A∩B) = P(A) · P(B)
C) P(B∩A) = P(A) · P(B|A)
D) P(B|A) = P(A|B)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
30
Twenty-eight percentof all people who take college statistics classes claim that they found a use for the class sometime during their college career.Of those who found a use for the class, 93% found gainful employment after graduation.Eighty-six percent of all people who take college statistics found gainful employment after graduation.What is the probability that a randomly selected student who took college statistics found a use for the class and found gainful employment after graduation?
A) 0.2604
B) 0.2408
C) 0.7998
D) 0.3500
A) 0.2604
B) 0.2408
C) 0.7998
D) 0.3500

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
31
Suppose you deal two cards from a standard deck of 52 cards.If you do not replace any cards between the deals, what is the probability you deal a king and then an even number (2, 4, 6, 8 or 10)?
A) 0.308
B) 0.384
C) 0.015
D) 0.030
A) 0.308
B) 0.384
C) 0.015
D) 0.030

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
32
Experts give a certain poorly performing professional sports team an 80% chance of winning at least one game during the upcoming regular season.Based on this prediction, what is the probability that the team will not win any games?
A) 4/5
B) 0.20
C) 0.19
D) 0.50
A) 4/5
B) 0.20
C) 0.19
D) 0.50

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
33
All event probabilities (defined as P here) must be:
A) P > 0.
B) P< 1.
C) 0 < P< 1.
D) 0 ≤ P ≤ 1.
A) P > 0.
B) P< 1.
C) 0 < P< 1.
D) 0 ≤ P ≤ 1.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
34
In a game of chance, two pyramid-shaped, four-sided dice (with sides 1, 2, 3, 4) are rolled and their individual totals are added.If the sum of the 2 four-sided dice exceeds 5 (result from die 1 + result from die 2 > 5), the roller wins.If the sum is 5 or less, the roller loses.What is the probability of winning on a single play?
A) 5/8
B) 3/16
C) 3/8
D) 1/2
A) 5/8
B) 3/16
C) 3/8
D) 1/2

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
35
All outcomes in the sample space that are not in event A can be described as:
A) event A corollary.
B) event A complement.
C) event A disjoint.
D) event A intersect.
A) event A corollary.
B) event A complement.
C) event A disjoint.
D) event A intersect.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
36
A computer security system requires a unique password for each user.The passwords use only letters of the English alphabet (26 possible letters) and cannot contain any repeats; that is, any given letter can be used only once in a password.If passwords have five letters each, how many passwords are available from which to choose?
A) 65,780
B) 11,881,376
C) 7,893,600
D) 130
A) 65,780
B) 11,881,376
C) 7,893,600
D) 130

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
37
What is the probability that you roll at least one six in four rolls of a die?
A) 5/6
B) 0.518
C) 0.482
D) 0.004
A) 5/6
B) 0.518
C) 0.482
D) 0.004

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
38
Two events that have no outcomes in common are said to be:
A) independent.
B) complementary events.
C) disjoint events.
D) intersecting events.
A) independent.
B) complementary events.
C) disjoint events.
D) intersecting events.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose that an ice cream shop offers a special deal one day: The price of a small ice cream cone will be determined by rolling a pair of ordinary, six-sided dice.The price (in cents) will be the larger number followed by the equal or smaller number.For example, if the first die shows a three and the second die a six, the piece of a cone will be 63 cents.If two fives are rolled, then the price is 55 cents. How many different prices are possible in the sample space for this situation?
A) 6
B) 21
C) 36
D) 50
A) 6
B) 21
C) 36
D) 50

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
40
A listing of all the possible outcomes from an experiment using set notation is called the:
A) experimental outcome list.
B) event.
C) sample space.
D) sample point.
A) experimental outcome list.
B) event.
C) sample space.
D) sample point.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
41
Suppose you have a group of 8 male and 4 female volunteers.How many ways are there to choose 6 of these volunteers for a treatment group?
A) 28
B) 32
C) 420
D) 924
A) 28
B) 32
C) 420
D) 924

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
42
Suppose a population contains 1,000,000 people, 5000 of whom have a disease.The table shows the number of people who have the disease and test positive, etc. 
Based on the table, what is the probability that a person who tests negative does not have the disease?
A) 99.99%
B) 97.7%
C) 92.6%
D) 6.2%

Based on the table, what is the probability that a person who tests negative does not have the disease?
A) 99.99%
B) 97.7%
C) 92.6%
D) 6.2%

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
43
If an ATM code consists of four numeric characters 0 to 9 inclusive, how many possible four-digit ATM codes are possible using the numbers 0 through 9?
A) 6561
B) 1,048,576
C) 100,000
D) 10,000
A) 6561
B) 1,048,576
C) 100,000
D) 10,000

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
44
Which of the following statements is true if and only if events A and B are disjoint?
A) P(A∪B) = P(A) + P(B)
B) P(A∩B) = P(A) ∙ P(B)
C)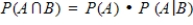
D)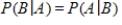
A) P(A∪B) = P(A) + P(B)
B) P(A∩B) = P(A) ∙ P(B)
C)
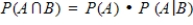
D)
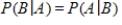

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose S = {E1, E2, E3, E4, E5, E6}.If we define set A (a subset of S) as A = {E1, E4}, then A can be best defined as:
A) an event.
B) a simple event.
C) the main event.
D) the sample space.
A) an event.
B) a simple event.
C) the main event.
D) the sample space.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
46
Which of the following is a reasonable estimate for the probability that Thanksgiving Day in the United States will be on a Thursday this year?
A) 0
B) 0.25
C) 0.5
D) 1
A) 0
B) 0.25
C) 0.5
D) 1

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
47
Suppose you deal two cards from a standard deck of 52 cards.If you replace the first card in the deck before you deal the second card, what is the probability you deal a face card (jack, queen, or king) and then an odd number (3, 5, 7 or 9)?
A) 0.071
B) 0.72
C) 0.75
D) 0.77
A) 0.071
B) 0.72
C) 0.75
D) 0.77

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
48
A simple event is:
A) something that simply happens.
B) an event consisting of exactly one outcome.
C) the most basic expression of the probabilistic process.
D) an event that has no complex outcomes.
A) something that simply happens.
B) an event consisting of exactly one outcome.
C) the most basic expression of the probabilistic process.
D) an event that has no complex outcomes.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
49
We know, based on past history, that 72% of all students who enter a particular university as freshmen will graduate in four years.If graduation rates and gender are independent, what proportion of female freshmen would we expect to graduate in four years?
A) More than 72%
B) Less than 72%
C) Roughly 72%
D) The percentage will depend on the proportion of female freshmen in the class.
A) More than 72%
B) Less than 72%
C) Roughly 72%
D) The percentage will depend on the proportion of female freshmen in the class.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
50
S = {E1, E2, E3, E4, E5, E6}.A = {E1, E4}.If S represents an equally likely outcome experiment, then what is P(A)?
A) 1/3
B) 2/3
C) 1/6
D) We need the individual simple event probabilities to solve the problem.
A) 1/3
B) 2/3
C) 1/6
D) We need the individual simple event probabilities to solve the problem.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
51
You wish to conduct a small survey to determine how fans feel about an upcoming ticket price increase to support an addition to the city's pro football stadium.Each person surveyed can make one of three responses: favor, oppose, or neutral.You survey three people independently.How many possible combined outcomes are there from this survey?
A) 6
B) 9
C) An infinite number of possibilities
D) 27
A) 6
B) 9
C) An infinite number of possibilities
D) 27

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
52
In an army platoon, a squad is being randomly chosen to go on patrol.The order of the selected participants matters, because it determines the positioning of each soldier; that is, the first chosen person will be the lead or the "point" man, with the second chosen following, and so on.If the source platoon consists of 16 soldiers and the squad being selected will have four soldiers, how many possible unique squads are there?
A) 43,680
B) 1820
C) 64
D) 65,536
A) 43,680
B) 1820
C) 64
D) 65,536

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
53
Suppose we know that for a particular population, the proportion of those age 65 and older who smoke is 0.21.We also know that the proportion of the same population who are younger than 65 and smoke is 0.10.What proportion of the population smokes?
A) 0.021
B) 0.31
C) 0.11
D) Need more information.
A) 0.021
B) 0.31
C) 0.11
D) Need more information.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
54
As used in the text, the term "experiment" is defined as:
A) an activity in which there is one outcome that is certain to occur.
B) an activity in which the uncertainty of the outcome is so great that we cannot hope to make reasonable predictions.
C) an activity in which there are at least two possible outcomes and the result of the activity cannot be predicted with absolute certainty.
D) an activity in which there are at most two possible outcomes and the result of the activity cannot be predicted with absolute certainty.
A) an activity in which there is one outcome that is certain to occur.
B) an activity in which the uncertainty of the outcome is so great that we cannot hope to make reasonable predictions.
C) an activity in which there are at least two possible outcomes and the result of the activity cannot be predicted with absolute certainty.
D) an activity in which there are at most two possible outcomes and the result of the activity cannot be predicted with absolute certainty.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck



