Deck 12: The Analysis of Variance

Question 1

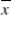is the:

A) second average of the ith sample.
B) average value of the second sample.
C) second population mean.
D) second weighted sample average.

Answer 1

average value of the second sample.

Question 2

Which of the following statements correctly describes the treatment sum of squares in one-way ANOVA?

A) It equals the number of columns (or rows) multiplied by the sum of the squared deviations of the row-block sample means from the grand mean.
B) It equals the number of rows (or columns) multiplied by the sum of the squared deviations of the column-block sample means from the grand mean.
C) It equals the sum of the square deviations between each block sample mean and the grand mean, multiplied by the number of observations made for each block, multiplied by the number of observations per cell.
D) It equals the sum of the squared deviations between each treatment sample mean and the grand mean, multiplied by the number of observations made for each treatment.

Answer 2

It equals the sum of the squared deviations between each treatment sample mean and the grand mean, multiplied by the number of observations made for each treatment.

Question 3

If interaction is present in the two-way ANOVA model and a test of factor A results in rejecting H₀, then:

A) the effect of factor A is not significant.
B) the effect of factor A is probably significant.
C) the effects of factor A and factor B are independent.
D) the effect of factor A is inconclusive.

Answer 3

the effect of factor A is probably significant.

Question 4

​ ​ What is the appropriate interpretation of this summary from a multiple comparison of means procedure?

A) None of the means appears to differ significantly.
B) Population B appears to have a larger mean than population A; and population C appears to have a larger mean than population A.
C) The mean of population B appears to be larger than the mean of population C, which appears to be larger than the mean of population D; and the mean of population D appears to be larger than the mean of population A.
D) The mean of population B appears to be larger than the mean of population A.

Question 5

A retailer is contemplating building a new store and has to choose between three general regions for construction (locations A, B, and C).To decide where to build, the retailer surveys five stores in each region and records the number of products sold over the same 3-day period at each of the 15 stores.The data appear below: (Given: MSE = 2740)
​ ​
Does there appear to be a difference in the mean number of products sold in at least two of the regions? Select the appropriate critical value (CV), test statistic (TS), and decision.(Use α = 0.05).

A) CV = 3.89; TS = 0.02611; fail to reject H₀
B) CV = 6.93; TS = 0.02611; fail to reject H₀
C) CV = 3.89; TS = 38.29; reject H₀
D) CV = 6.93; TS = 38.29; reject H₀

Question 6

In a one-way ANOVA, if the null hypothesis is H₀: μ1 = μ2 = μ3 = μ4, then the alternative hypothesis is:

A) Ha: μ1 ≠ μ2 ≠ μ3 ≠ μ4.
B) Ha: None of the population means differs.
C) Ha: At least two of the population means differ.
D) Ha: At least one of the population means differs.

Question 7

We wish to evaluate the effectiveness of a certain drug on humans.We create a two-way ANOVA design with factor A = gender, factor B = dosage, and response variable = health.If there is a significant dosage/gender interaction, which of the following statements accurately describes this relationship?

A) The relationship between dosage and health is the same for men and women.
B) The relationship between dosage and health differs for men and women.
C) There is most likely a relationship between health and gender.
D) There is most likely a relationship between health and dosage.

Question 8

MSA (mean square due to factor) is an unbiased estimator of the common variance σ2 if:

A) the population means are different.
B) H₀ is true in reality.
C) H₀ is rejected.
D) the assumption of normality is met.

Question 9

If interaction is present in the two-way ANOVA model and a test of factor A results in failing to reject H₀, then:

A) the effect of factor A is not significant.
B) the effect of factor A is probably significant.
C) the effects of factor A and factor B are independent.
D) the effect of factor A is inconclusive.

Question 10

In the one-way ANOVA, the total variability is expressed as a sum of variabilities about different mean values.These component variabilities are called:

A) SSA (sum of squares due to analysis) and SSE (sum of squares due to error).
B) SST (total sum of squares) and SSE (sum of squares due to error).
C) SSR (sum of squares due to regression) and SST (total sum of squares).
D) SSA (sum of squares due to factor) and SSE (sum of squares due to error).

Question 11

Why is it necessary to adjust the individual confidence level of each confidence interval for a multiple comparison of means procedure?

A) The total probability of the intervals being correct will always be less than the probability of any single confidence interval covering a single mean difference.
B) Each confidence interval is slightly biased and the correction will alleviate that bias.
C) The intervals will not be able to detect slight differences in means without a correction.
D) Confidence intervals are always estimates; so, when considering of them, an adjustment is needed to allow for valid inference.

Question 12

What are the correct assumptions for the two-way ANOVA procedure?

A) The sample sizes are large (n≥ 30), and all of the (a) × (b) populations under consideration are normal.
B) Samples are selected randomly and independently from (a) × (b) population distributions, which are all normal and have equal variance.
C) Samples are random, from normal populations, and large (n ≥ 30).
D) Population variances are known to be equal, samples are random, and sample size is sufficiently large such that the population distribution is of no consequence.