Deck 18: Introduction to Quantum Mechanics
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/43
Play
Full screen (f)
Deck 18: Introduction to Quantum Mechanics
1
A particle is in the first excited state of a one-dimensional box of length 1.0 m.What is the minimum value of its momentum (in kg . m/s)?
A)3.3 *10-34
B)6.6 * 10-34
C)9.9 * 10-34
D)13 * 10-34
E)22 *10-34
A)3.3 *10-34
B)6.6 * 10-34
C)9.9 * 10-34
D)13 * 10-34
E)22 *10-34
6.6 * 10-34
2
If the interaction of a particle with its environment restricts the particle to a finite region of space, the result is the quantisation of ____ of the particle.
A)the momentum
B)the energy
C)the velocity
D)all of the above properties
E)only properties (a) and (b)
A)the momentum
B)the energy
C)the velocity
D)all of the above properties
E)only properties (a) and (b)
all of the above properties
3
A particle is in the second excited state of a one-dimensional box of length 1.0 m.What is its momentum (in kg . m/s)?
A)6.6 *10-34
B)3.3 * 10-34
C)9.9 *10-34
D)13 * 10-34
E)cannot be solved unless mass of particle is known
A)6.6 *10-34
B)3.3 * 10-34
C)9.9 *10-34
D)13 * 10-34
E)cannot be solved unless mass of particle is known
9.9 *10-34
4
The wave function for a particle in a one-dimensional box is .Which statement is correct? 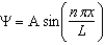
A)This wave function gives the probability of finding the particle at x.
B)| (x)|2 gives the probability of finding the particle at x.
C)| (x)|2 x gives the probability of finding the particle between x and x + x.
D)gives the probability of finding the particle at a particular value of x.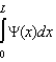
E)gives the probability of finding the particle between x and x + x.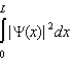
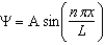
A)This wave function gives the probability of finding the particle at x.
B)| (x)|2 gives the probability of finding the particle at x.
C)| (x)|2 x gives the probability of finding the particle between x and x + x.
D)gives the probability of finding the particle at a particular value of x.
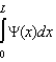
E)gives the probability of finding the particle between x and x + x.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
5
When the potential energy of a system is independent of time, the wave function of the system:
A)is a constant.
B)is directly proportional to the time.
C)cannot be normalised.
D)depends only on the centre of mass, , of the system.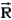
E)depends on the vector positions, i, of each particle in the system.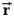
A)is a constant.
B)is directly proportional to the time.
C)cannot be normalised.
D)depends only on the centre of mass, , of the system.
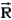
E)depends on the vector positions, i, of each particle in the system.
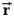

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
6
A particle is in the ground state of a one-dimensional box of length 1.0 m.What is the minimum value of its momentum (in kg .m/s)?
A)9.9 * 10-34
B)6.6 * 10-34
C)3.3 * 10-34
D)13 * 10-34
E)cannot be solved unless mass of particle is known.
A)9.9 * 10-34
B)6.6 * 10-34
C)3.3 * 10-34
D)13 * 10-34
E)cannot be solved unless mass of particle is known.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
7
The ground state energy of a harmonic oscillator is:
A)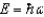
B)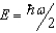
C)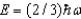
D)E = 0
E)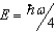
A)
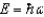
B)
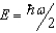
C)
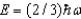
D)E = 0
E)
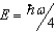

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
8
A 15-kg mass, attached to a massless spring whose force constant is 2500 N/m, has an amplitude of 4 cm.Assuming the energy is quantised, find the quantum number of the system, n, if En = nhf.
A)1.5 *1033
B)3.0 * 1033
C)4.5 * 1033
D)5.4 * 1033
E)1.0 * 1033
A)1.5 *1033
B)3.0 * 1033
C)4.5 * 1033
D)5.4 * 1033
E)1.0 * 1033

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
9
What is the quantum number n of a particle of mass m confined to a one-dimensional box of length L when its momentum is 4h/L?
A)1
B)4
C)2
D)8
E)16
A)1
B)4
C)2
D)8
E)16

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
10
Classically, the concept of 'tunneling' is impossible.Why?
A)The kinetic energy of the particle would be negative.
B)The velocity of the particle would be negative.
C)The total energy of a particle is equal to the kinetic and potential energies.
D)The kinetic energy must be equal to the potential energy.
E)The total energy for the particle would be negative.
A)The kinetic energy of the particle would be negative.
B)The velocity of the particle would be negative.
C)The total energy of a particle is equal to the kinetic and potential energies.
D)The kinetic energy must be equal to the potential energy.
E)The total energy for the particle would be negative.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
11
Find the kinetic energy (in terms of Planck's constant) of a football (m = 1 kg) confined to a one-dimensional box that is 25 cm wide if the baseball can be treated as a wave in the ground state.
A)3 h2
B)2 h2
C)h2
D)4h2
E)0.5 h2
A)3 h2
B)2 h2
C)h2
D)4h2
E)0.5 h2

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
12
The average position, or expectation value, of a particle whose wave function (x) depends only on the value of x, is given by < x > =
A)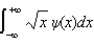
B)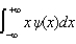
C)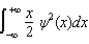
D)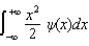
E)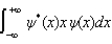
A)
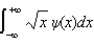
B)
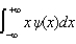
C)
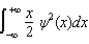
D)
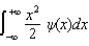
E)
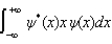

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
13
A physically reasonable wave function, (x), for a one-dimensional system must:
A)be defined at all points in space.
B)be continuous at all points in space.
C)be single-valued.
D)obey all the constraints listed above.
E)obey only (b) and (c) above.
A)be defined at all points in space.
B)be continuous at all points in space.
C)be single-valued.
D)obey all the constraints listed above.
E)obey only (b) and (c) above.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
14
What is the quantum number n of a particle of mass m confined to a one-dimensional box of length L when its energy is 2 h2/mL2?
A)2
B)8
C)4
D)1
E)16
A)2
B)8
C)4
D)1
E)16

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
15
The wave function for a particle confined to a one-dimensional box located between x = 0 and x = L is given by (x) = A sin (n x/L) + B cos (n x/L) .The constants A and B are determined to be:
A), 0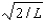
B),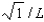
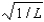
C)0,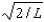
D),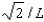
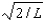
E)2/L, 0
A), 0
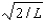
B),
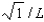
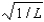
C)0,
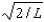
D),
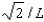
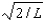
E)2/L, 0

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
16
The expectations value of a function f(x) of x when the wave function depends only on x is given by < f(x) > =
A)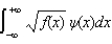
B)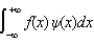
C)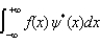
D)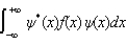
E)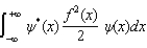
A)
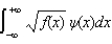
B)
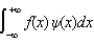
C)
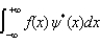
D)
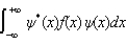
E)

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
17
Calculate the ground state energy (in eV) for an electron in a box (an infinite well) having a width of 0.050 nm.
A)10
B)75
C)24
D)150
E)54
A)10
B)75
C)24
D)150
E)54

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
18
When a particle approaching a potential step has a total energy that is greater than the potential step, what is the probability that the particle will be reflected?
A)P < 0.
B)P = 0.
C)P = 1.
D)P > 0.
E)P = .
A)P < 0.
B)P = 0.
C)P = 1.
D)P > 0.
E)P = .

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
19
The fact that we can only calculate probabilities for values of physical quantities in quantum measurements means that:
A)radiation and matter are not described by mathematical relations between measurements.
B)the probabilities cannot be calculated from mathematical relationships.
C)the results of physical measurements bear no relationship to theory.
D)the average values of a large number of measurements correspond to the calculated probabilities.
E)the average of the values calculated in a large number of different theories corresponds to the results of a measurement.
A)radiation and matter are not described by mathematical relations between measurements.
B)the probabilities cannot be calculated from mathematical relationships.
C)the results of physical measurements bear no relationship to theory.
D)the average values of a large number of measurements correspond to the calculated probabilities.
E)the average of the values calculated in a large number of different theories corresponds to the results of a measurement.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
20
A particle has a total energy that is less than that of a potential barrier.When the particle penetrates the barrier, its wave function is:
A)a positive constant.
B)exponentially increasing.
C)oscillatory.
D)exponentially decreasing.
E)none of the above.
A)a positive constant.
B)exponentially increasing.
C)oscillatory.
D)exponentially decreasing.
E)none of the above.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
21
When U(x) is infinitely large elsewhere, the wave function of a particle restricted to the region 0 < x < L where U(x) = 0, may have the form (x) =
A)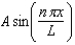
B)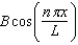
C)Aen x / L.
D)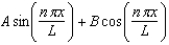
E)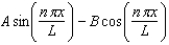
A)
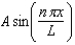
B)
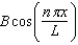
C)Aen x / L.
D)
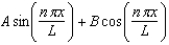
E)
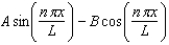

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
22
If the position of an electron (m = 9.11 *10-31 kg) could be measured to within 10-30 m, the uncertainty in the magnitude of its speed could be as much as
A)6 *10-34 m/s.
B)6 *1025 m/s.
C)6 * 1030 m/s.
D)1031 m/s.
E)1061 m/s.
A)6 *10-34 m/s.
B)6 *1025 m/s.
C)6 * 1030 m/s.
D)1031 m/s.
E)1061 m/s.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
23
The graph below represents a wave function (x) for a particle confined to -2.00 m x +2.00 m.The value of the normalisation constant A may be: 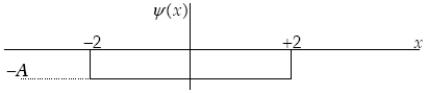
A)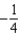
B)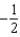
C)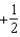
D)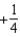
E)either or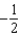
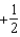

A)
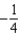
B)
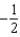
C)
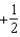
D)
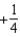
E)either or
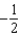
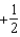

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
24
The wave function (x) of a particle confined to 0 x L is given by (x) = Ax. (x) = 0 for x < 0 and x > L.When the wave function is normalised, the probability density at coordinate x has the value:
A)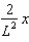
B)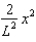
C)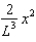
D)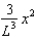
E)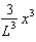
A)
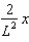
B)
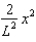
C)
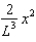
D)
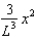
E)
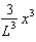

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
25
Frank says that quantum mechanics does not apply to cricket balls because they do not jump from quantum state to quantum state when being thrown.Francine agrees with him.She says that there is no uncertainty in a cricket ball's position or momentum.Are they correct, or not, and why?
A)They are correct because the first excited state of a cricket ball is at a higher energy that any cricket ball ever receives.Therefore we cannot determine whether or not there is uncertainty in its position or momentum.
B)They are correct because the first excited state of a cricket ball is at a higher energy that any cricket ball ever receives.Therefore its position and momentum are completely uncertain until it is caught.
C)They are wrong because the cricket ball goes through so many quantum states in being thrown that we cannot observe the transitions.The uncertainties in its position and momentum are too small to observe.
D)They are wrong because the cricket ball goes through so many quantum states in being thrown that we cannot observe the transitions.Because of the number of transitions its position and momentum are completely uncertain until it is caught.
E)Quantum mechanics states that they are correct as long as they do not make any observations, but wrong as soon as they begin to make observations.
A)They are correct because the first excited state of a cricket ball is at a higher energy that any cricket ball ever receives.Therefore we cannot determine whether or not there is uncertainty in its position or momentum.
B)They are correct because the first excited state of a cricket ball is at a higher energy that any cricket ball ever receives.Therefore its position and momentum are completely uncertain until it is caught.
C)They are wrong because the cricket ball goes through so many quantum states in being thrown that we cannot observe the transitions.The uncertainties in its position and momentum are too small to observe.
D)They are wrong because the cricket ball goes through so many quantum states in being thrown that we cannot observe the transitions.Because of the number of transitions its position and momentum are completely uncertain until it is caught.
E)Quantum mechanics states that they are correct as long as they do not make any observations, but wrong as soon as they begin to make observations.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
26
A particle in a finite potential well has energy E, as shown below. 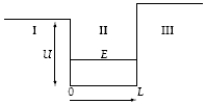 The wave function in region I where x < 0 has the form I =
The wave function in region I where x < 0 has the form I =
A)Ae-Cx.
B)AeCx.
C)F sin kx.
D)G cos kx.
E)F sin kx + G cos kx.
 The wave function in region I where x < 0 has the form I =
The wave function in region I where x < 0 has the form I =A)Ae-Cx.
B)AeCx.
C)F sin kx.
D)G cos kx.
E)F sin kx + G cos kx.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
27
An electron has been accelerated by a potential difference of 100 V.If its position is known to have an uncertainty of 1 nm, what is the percent uncertainty ( p/p *100) of the electron's momentum?
A)1%
B)2%
C)10%
D)>>10%
E)5%
A)1%
B)2%
C)10%
D)>>10%
E)5%

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
28
Assume we can determine the position of a particle within an uncertainty of 0.5 nm.What will be the resulting uncertainty in the particle's momentum (in kg . m/s)?
A)1.9 *10-25
B)4.2 *10-25
C)1.1 * 10-25
D)1.3 *10-24
E)6.6 *10-25
A)1.9 *10-25
B)4.2 *10-25
C)1.1 * 10-25
D)1.3 *10-24
E)6.6 *10-25

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
29
The graph below represents a wave function (x) for a particle confined to -4.00 m x +4.00 m.The magnitude of the normalisation constant A is: 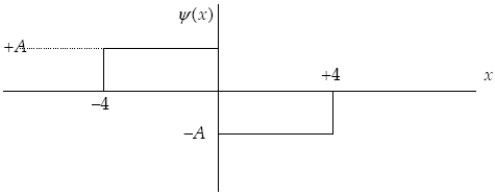
A)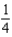
B)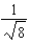
C)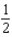
D)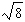
E)4.

A)
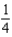
B)
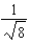
C)
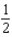
D)
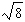
E)4.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
30
Because the factor h on the right side of the Heisenberg uncertainty principle has units of Joule-seconds, it suggests that the energy of a system also has uncertainty.The uncertainty in energy depends on the length of the time interval during which a system exists. E t h/4 .Suppose an unstable mass is produced during a high-energy collision such that the uncertainty in its mass is me/100.(me = 9.11*10-31 kg.) How long will this particle exist?
A)6.4 * 10-20 s
B)2.3 * 10-23 s
C)1.0 * 1015 s
D)1.2 *1013 s
E)8.1 * 10-19 s
A)6.4 * 10-20 s
B)2.3 * 10-23 s
C)1.0 * 1015 s
D)1.2 *1013 s
E)8.1 * 10-19 s

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
31
Find the uncertainty in the momentum (in kg .m/s) of an electron if the uncertainty in its position is equal to 3.4 * 10-10 m, the circumference of the first Bohr orbit.
A)6.2 * 10-25
B)1.6 * 10-25
C)15.5 * 10-25
D)19.4 * 10-25
E)2.0 * 10-24
A)6.2 * 10-25
B)1.6 * 10-25
C)15.5 * 10-25
D)19.4 * 10-25
E)2.0 * 10-24

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
32
The wave function for a particle in a box of length L is given by .If the box extends from x = 0 to x = L, What is the probability of finding the particle between x = 0.60 L and x = 0.70 L? 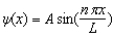
A)0.10
B)0.20
C)0.25
D)0.05
E)The probability is not given.
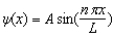
A)0.10
B)0.20
C)0.25
D)0.05
E)The probability is not given.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
33
Assume the Heisenberg uncertainty principle can take the form E t h/4.How accurate can the position of an electron be made if its speed is 5* 106 m/s and if the uncertainty in its energy is 10 eV?
A)7.7 *10-18 m
B)1.3 * 10-23 m
C)6.2 * 10-15 m
D)1.6 * 10-10 m
E)1.2 * 10-9 m
A)7.7 *10-18 m
B)1.3 * 10-23 m
C)6.2 * 10-15 m
D)1.6 * 10-10 m
E)1.2 * 10-9 m

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
34
A particle in a finite potential well has energy E, as shown below. 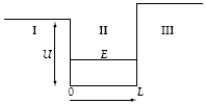 The wave function in region II where x > 0 has the form II =
The wave function in region II where x > 0 has the form II =
A)Ae-Cx.
B)AeCx.
C)F sin kx.
D)G cos kx.
E)F sin kx + G cos kx.
 The wave function in region II where x > 0 has the form II =
The wave function in region II where x > 0 has the form II =A)Ae-Cx.
B)AeCx.
C)F sin kx.
D)G cos kx.
E)F sin kx + G cos kx.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
35
The wave function for a particle in a box of length L is given by .If the box extends from x = 0 to x = L, at which of the following positions is the highest probability for finding the particle? 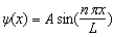
A)x = 0.33 L
B)x = 0.04 L
C)x = 0.60 L
D)Both (a) and (b).
E)Both (b) and (c).
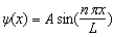
A)x = 0.33 L
B)x = 0.04 L
C)x = 0.60 L
D)Both (a) and (b).
E)Both (b) and (c).

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
36
A baseball (1 kg) has an energy of 100 joules.If its uncertainty in position is 1 m, what is the percentage uncertainty ( p/p * 100) in the momentum of the baseball?
A)<<1%
B)1%
C)2%
D)5%
E)10%
A)<<1%
B)1%
C)2%
D)5%
E)10%

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
37
The graph below shows the value of the probability density (x)|2 in the region-3.00 m x +3.00 m.The value of the constant A is: 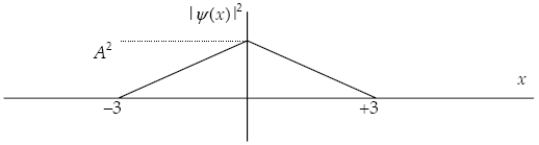
A)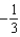
B)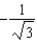
C)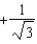
D)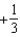
E)either or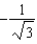
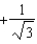

A)
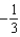
B)
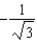
C)
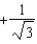
D)
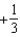
E)either or
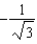
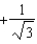

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
38
Quantum tunnelling occurs in:
A)nuclear fusion.
B)radioactive decay by emission of alpha particles.
C)the scanning tunnelling microscope.
D)nuclear fusion, radioactive decay and in the scanning tunnelling microscope.
E)radioactive decay and the scanning tunnelling microscope only.
A)nuclear fusion.
B)radioactive decay by emission of alpha particles.
C)the scanning tunnelling microscope.
D)nuclear fusion, radioactive decay and in the scanning tunnelling microscope.
E)radioactive decay and the scanning tunnelling microscope only.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
39
A particle in a finite potential well has energy E, as shown below. 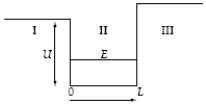 The wave function in region III where x > L has the form III =
The wave function in region III where x > L has the form III =
A)Ae-Cx.
B)AeCx.
C)F sin kx.
D)G cos kx.
E)F sin kx + G cos kx.
 The wave function in region III where x > L has the form III =
The wave function in region III where x > L has the form III =A)Ae-Cx.
B)AeCx.
C)F sin kx.
D)G cos kx.
E)F sin kx + G cos kx.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
40
The graph below represents a wave function (x) for a particle confined to -2.00 m x +2.00 m.The value of the normalisation constant A may be: 
A)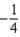
B)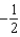
C)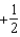
D)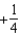
E)either or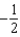
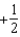

A)
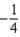
B)
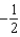
C)
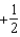
D)
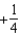
E)either or
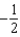
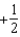

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
41
Because of Heisenberg's Uncertainty Principle, the velocity of a particle is known least precisely when the length of the wave packet representing the particle is:
A)< 10-15 m.
B)< 10-10 m.
C)of the order of 1.00 m.
D)>10 m.
E)the length of a plane wave (infinite)
A)< 10-15 m.
B)< 10-10 m.
C)of the order of 1.00 m.
D)>10 m.
E)the length of a plane wave (infinite)

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
42
Suppose we use optical radiation ( = 500 nm) to determine the position of the electron to within the wavelength of the light.What will be the resulting uncertainty in the electron's velocity?

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
43
An electron is sitting on a pinpoint having a diameter of 2.5 m.What is the minimum uncertainty in the speed of the electron?

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck



