Deck 2: Vector Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/57
Play
Full screen (f)
Deck 2: Vector Analysis
1
Three vectors A, B, and C, drawn in a head-to-tail fashion, form three sides of a triangle. What is A + B + C What is A + B C
Draw vector diagram using three vectors
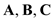 in a head to tail fashion:
in a head to tail fashion:
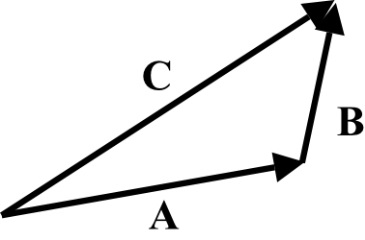 Figure 1
Figure 1
In Head-to-tail rule, the value of sum of two vectors
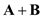 is
is
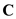 . But when we draw the three vectors
. But when we draw the three vectors
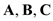 in head-to-tail rule forms the three sides of a triangle is shown in Figure 1. When
in head-to-tail rule forms the three sides of a triangle is shown in Figure 1. When
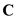 is in opposite direction. The value of sum of two vectors
is in opposite direction. The value of sum of two vectors
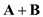 is
is
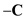 .
.
Calculate the value of sum of vectors,
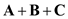 .
.
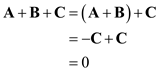 Therefore, the value of vector
Therefore, the value of vector
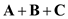 is
is
 .
.
Calculate the value of sum of vectors,
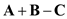 .
.
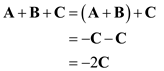 Therefore, the value of vector
Therefore, the value of vector
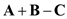 is
is
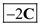 .
.
 in a head to tail fashion:
in a head to tail fashion: Figure 1
Figure 1In Head-to-tail rule, the value of sum of two vectors
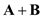 is
is 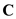 . But when we draw the three vectors
. But when we draw the three vectors 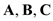 in head-to-tail rule forms the three sides of a triangle is shown in Figure 1. When
in head-to-tail rule forms the three sides of a triangle is shown in Figure 1. When 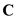 is in opposite direction. The value of sum of two vectors
is in opposite direction. The value of sum of two vectors 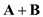 is
is 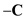 .
.Calculate the value of sum of vectors,
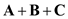 .
.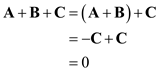 Therefore, the value of vector
Therefore, the value of vector 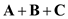 is
is  .
.Calculate the value of sum of vectors,
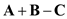 .
.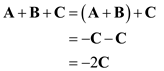 Therefore, the value of vector
Therefore, the value of vector 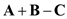 is
is 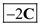 .
. 2
Given two points P 1 ( 2, 0, 3) and P 2 (0, 4, 1), find
a) the length of the line joining P 1 and P 2 , and
b) the perpendicular distance from the point P 3 (3, 1, 3) to the line.
a) the length of the line joining P 1 and P 2 , and
b) the perpendicular distance from the point P 3 (3, 1, 3) to the line.
(a)
Consider the points
 as
as
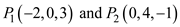 .
.
Write the expression for the vector,
 .
.
 Write the expression for the vector,
Write the expression for the vector,
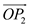 .
.
 Calculate the vector,
Calculate the vector,
 .
.
 Calculate the magnitude of the vector,
Calculate the magnitude of the vector,
 .
.
 Therefore, the length of the line joining
Therefore, the length of the line joining
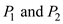 ,
,
 is
is
 .
.
(b)
Consider a point
 as shown in Figure 1 and draw a perpendicular from this point to line
as shown in Figure 1 and draw a perpendicular from this point to line
 which meets at point
which meets at point
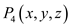 .
.
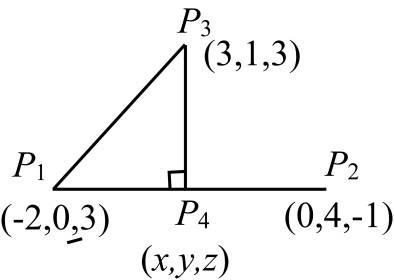 Figure 1
Figure 1
The perpendicular distance from the point
 to the line is
to the line is
 , which equals
, which equals
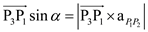 .
.
Therefore,
 …… (1)
…… (1)
Write the expression for the vector,
 .
.
 Calculate the vector,
Calculate the vector,
 .
.
 Substitute the known values in equation (1).
Substitute the known values in equation (1).

 Therefore, the perpendicular distance from
Therefore, the perpendicular distance from
 to the line,
to the line,
 is
is
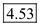 .
.
Consider the points
 as
as 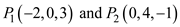 .
.Write the expression for the vector,
 .
. Write the expression for the vector,
Write the expression for the vector, 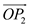 .
. Calculate the vector,
Calculate the vector,  .
. Calculate the magnitude of the vector,
Calculate the magnitude of the vector,  .
. Therefore, the length of the line joining
Therefore, the length of the line joining 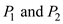 ,
,  is
is  .
.(b)
Consider a point
 as shown in Figure 1 and draw a perpendicular from this point to line
as shown in Figure 1 and draw a perpendicular from this point to line which meets at point
which meets at point 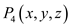 .
. Figure 1
Figure 1The perpendicular distance from the point
 to the line is
to the line is  , which equals
, which equals 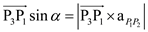 .
.Therefore,
 …… (1)
…… (1)Write the expression for the vector,
 .
. Calculate the vector,
Calculate the vector,  .
. Substitute the known values in equation (1).
Substitute the known values in equation (1).
 Therefore, the perpendicular distance from
Therefore, the perpendicular distance from  to the line,
to the line,  is
is 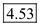 .
. 3
What are the expressions for A · B and A × B in Cartesian coordinates
Write expressions for vectors
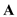 and
and
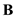 in Cartesian coordinates.
in Cartesian coordinates.
 Calculate the expression for
Calculate the expression for
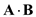 in Cartesian coordinates.
in Cartesian coordinates.
 Therefore, the expression for
Therefore, the expression for
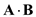 in Cartesian coordinates is
in Cartesian coordinates is
 .
.
Calculate the expression for
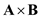 in Cartesian coordinates.
in Cartesian coordinates.
 Therefore, the expression for
Therefore, the expression for
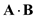 in Cartesian coordinates is
in Cartesian coordinates is
 .
.
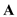 and
and 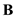 in Cartesian coordinates.
in Cartesian coordinates. Calculate the expression for
Calculate the expression for 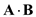 in Cartesian coordinates.
in Cartesian coordinates. Therefore, the expression for
Therefore, the expression for 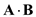 in Cartesian coordinates is
in Cartesian coordinates is  .
.Calculate the expression for
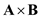 in Cartesian coordinates.
in Cartesian coordinates. Therefore, the expression for
Therefore, the expression for 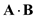 in Cartesian coordinates is
in Cartesian coordinates is  .
. 4
State the divergence theorem in words.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
5
A rhombus is an equilateral parallelogram. Denote two neighboring sides of a rhombus by vectors A and B.
a) Verify that the two diagonals are A + B and A B.
b) Prove that the diagonals are perpendicular to each other.
a) Verify that the two diagonals are A + B and A B.
b) Prove that the diagonals are perpendicular to each other.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
6
Does A × B = A × C imply B = C Explain.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
7
Given a vector field A = a r r + a z z ,
a) find the total outward flux over a circular cylinder around the z-axis with a radius 2 and a height 4 centered at origin.
b) Repeat (a) for the same cylinder with its base coinciding with the xy -plane.
c) Find · A and verify the divergence theorem.
a) find the total outward flux over a circular cylinder around the z-axis with a radius 2 and a height 4 centered at origin.
b) Repeat (a) for the same cylinder with its base coinciding with the xy -plane.
c) Find · A and verify the divergence theorem.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
8
What is the physical definition of the curl of a vector field

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
9
Under what conditions can the dot product of two vectors be negative

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
10
The cylindrical coordinates of two points P 1 and P 2 are: P 1 (4, 60°, 1) and P 2 (3, 180°, 1). Determine the distance between these two points.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
11
Find the results of the following products of unit vectors:
a) a , · a x ,
b) a R · a y ,
c) a z · a R ,
d) a × a x ,
e) a r × a R ,
f) a × a z.
a) a , · a x ,
b) a R · a y ,
c) a z · a R ,
d) a × a x ,
e) a r × a R ,
f) a × a z.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
12
State Stokes's theorem in words.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
13
Compare the values of the following scalar triple products of vectors:
(a) (A × C)·B ,
(b) A·(C × B) ,
(c) (A × B)·C , and
(d) B·(a A × A).
(a) (A × C)·B ,
(b) A·(C × B) ,
(c) (A × B)·C , and
(d) B·(a A × A).

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
14
Given vector A = a x 5 a y 2 + a z , find the expression of
a) a unit vector a B such that a B || A, and
b) a unit vector a C in the xy -plane such that a C A.
a) a unit vector a B such that a B || A, and
b) a unit vector a C in the xy -plane such that a C A.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
15
What is the difference between a scalar quantity and a scalar field Between a vector quantity and a vector field

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
16
Find the divergence of the following radial vector fields:
a) f 1 ( R ) = a R R n ,
b)
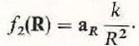
a) f 1 ( R ) = a R R n ,
b)
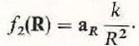

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
17
If the three sides of an arbitrary triangle are denoted by vectors A, B, and C in a clockwise or counterclockwise direction, then the equation A + B + C = 0 holds. Prove the law of sines.
HINT: Cross multiply the equation separately by A and by B , and examine the magnitude relations of the products.
HINT: Cross multiply the equation separately by A and by B , and examine the magnitude relations of the products.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
18
What makes a coordinate system (a) orthogonal and (b) right-handed

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
19
Find the clockwise circulation of the vector field F given in Example 2-14 around a square path in the xy -plane centered at the origin and having four units on each side ( 2 x 2 and 2 y 2).
Example

Example


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
20
What is the difference between an irrotational field and a solenoidal field

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
21
Write down the results of A · B and A × B if (a) A || B , and (b) A B.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
22
Transform Cartesian coordinates (4, 6, 12) into spherical coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
23
Express the r-component, A r , of a vector A at ( r 1 1 , z 1 )
a) in terms of A x and A y in Cartesian coordinates, and
b) in terms of A R and A in spherical coordinates.
a) in terms of A x and A y in Cartesian coordinates, and
b) in terms of A R and A in spherical coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
24
State Helmholtz's theorem in words.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
25
Which of the following expressions do not make sense
(a) A × B/|B| ,
(b) C · D/(A × B) ,
(c) AB/CD ,
(d) A × B/(C · D) ,
(e) ABC,
(f) A × B × C.
(a) A × B/|B| ,
(b) C · D/(A × B) ,
(c) AB/CD ,
(d) A × B/(C · D) ,
(e) ABC,
(f) A × B × C.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
26
Decompose vector A = a x 2 a y 5+ a z 3 into two components, A 1 and A 2 , that are, respectively, perpendicular and parallel to another vector B = a x + a y 4.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
27
What is the physical definition of the gradient of a scalar field

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
28
For vector function A = a r r 2 + a z 2 z , verify the divergence theorem for the circular cylindrical region enclosed by r = 5, z = 0, and z = 4.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
29
Given three vectors A, B, and C as follows:
A = a x 6 + a y 2 a z 3,
B = a x 4 a y 6 + a z 12,
C = a x 5 a z 2,
find
a) a B ,
b) |B A|,
c) the component of A in the direction of B ,
d) B · A,
e) the component of B in the direction of A ,
f) AB ,
g) A × C, and
h) A · (B × C) and (A × B) · C.
A = a x 6 + a y 2 a z 3,
B = a x 4 a y 6 + a z 12,
C = a x 5 a z 2,
find
a) a B ,
b) |B A|,
c) the component of A in the direction of B ,
d) B · A,
e) the component of B in the direction of A ,
f) AB ,
g) A × C, and
h) A · (B × C) and (A × B) · C.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
30
What are metric coefficients

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
31
Given F = a r sin + a 3 cos and the quarter-circular region shown in Fig. 2-22,
a) determine
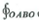 F · d , and
F · d , and
b) find × F , and verify Stokes's theorem.
Fig Path for line integral (Example 2-14 and 2-16)
 Example 1
Example 1
 Example 2
Example 2

a) determine
 F · d , and
F · d , andb) find × F , and verify Stokes's theorem.
Fig Path for line integral (Example 2-14 and 2-16)
 Example 1
Example 1  Example 2
Example 2 

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
32
A vector field D = a R (cos 2 )/ R 3 exists in the region between two spherical shells defined by R = 1 and R = 2. Evaluate
a)
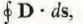
b) • D d v.
a)
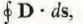
b) • D d v.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
33
Is (A · B)C equal to A(B · C) Explain.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
34
Derive the formula for the surface of a sphere with a radius R 0 by integrating the differential surface area in spherical coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
35
Express the -component, E , of a vector E at ( R 1 , l , l )
a) in terms of E x , E y , and E z in Cartesian coordinates, and
b) In terms of E r and E z in cylindrical coordinates.
a) in terms of E x , E y , and E z in Cartesian coordinates, and
b) In terms of E r and E z in cylindrical coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
36
For a scalar function f and a vector function A, prove that
• ( f A ) = f • A + A • f
in Cartesian coordinates.
• ( f A ) = f • A + A • f
in Cartesian coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
37
Given a vector B = a x 2 a y 6 + a z 3, find
a) the magnitude of B ,
b) the expression for a B ,
c) the angles that B makes with the x, y , and z axes.
a) the magnitude of B ,
b) the expression for a B ,
c) the angles that B makes with the x, y , and z axes.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
38
Equation (2-15) in Example 2-2 describes the scalar triple products of three vectors A, B, and C. There is another important type of product of three vectors. It is a vector triple product, A × (B × C). Prove the following relation by expansion in Cartesian coordinates:
A × (B × C) = B(A · C)-C(A · B). (2-113)
Equation (2-113) is known as the "BAC-CAB" rule.
A × (B × C) = B(A · C)-C(A · B). (2-113)
Equation (2-113) is known as the "BAC-CAB" rule.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
39
Express the space rate of change of a scalar in a given direction in terms of its gradient.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
40
Let unit vectors a A and a B denote the directions of vectors A and B in the xy -plane that make angles and , respectively, with the x -axis.
a) Obtain a formula for the expansion of the cosine of the difference of two angles, cos ( ), by taking the scalar product a A · a B.
b) Obtain a formula for sin ( ) by taking the vector product a B × a A.
a) Obtain a formula for the expansion of the cosine of the difference of two angles, cos ( ), by taking the scalar product a A · a B.
b) Obtain a formula for sin ( ) by taking the vector product a B × a A.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
41
Write d and dv (a) in Cartesian coordinates, (b) in cylindrical coordinates, and (c) in spherical coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
42
Prove the identity in Eq.(2-105) in Cartesian coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
43
Given two vectors A and B , how do you find (a) the component of A in the direction of B , and (b) the component of B in the direction of A

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
44
Assuming V = xy 2 yz, find, at point P (2, 3, 6),
a) the direction and the magnitude of the maximum increase of V, and
b) the space rate of decrease of V in the direction toward the origin.
a) the direction and the magnitude of the maximum increase of V, and
b) the space rate of decrease of V in the direction toward the origin.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
45
Given a vector field in spherical coordinates F = a R (12/ R 2 ).

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
46
Given two points P 1 (l, 2, 0) and P 2 ( 3, 4, 0) in Cartesian coordinates with origin O , find
a) the length of the projection of
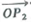 on
on
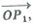 and
and
b) the area of the triangle OP 1 P 2.
a) the length of the projection of
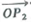 on
on 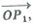 and
andb) the area of the triangle OP 1 P 2.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
47
Find the component of the vector A = a x z a z x at the point P 1 ,( 1, 0, 2) that is directed toward the point
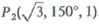 .
.
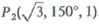 .
.
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
48
What is the expression for the del operator, , in Cartesian coordinates

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
49
The three corners of a right triangle are at P 1 (1, 0, 2), P 2 ( 3, 1, 5), and P 3 (3, 4, 6).
a) Determine which corner is a right angle.
b) Find the area of the triangle.
a) Determine which corner is a right angle.
b) Find the area of the triangle.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
50
10 Given two points P 1 (l, 2, 3) and P 2 ( 1, 0, 2) in Cartesian coordinates, write the expressions of the vectors
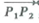 and
and
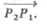
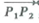 and
and 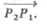

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
51
Prove the identity in Eq. (2-109) in Cartesian coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
52
Does A · B = A · C imply B = C Explain.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
53
Solve Example 2-10 in cylindrical coordinates.
Example 2-10

Example 2-10


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
54
What is the physical definition of the divergence of a vector field

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
55
Express the position vector
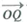 from the origin O to the point Q (3, 4, 5) in cylindrical coordinates.
from the origin O to the point Q (3, 4, 5) in cylindrical coordinates.
 from the origin O to the point Q (3, 4, 5) in cylindrical coordinates.
from the origin O to the point Q (3, 4, 5) in cylindrical coordinates.
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
56
The position of a point in cylindrical coordinates is given by (3, 4 /3, 4). Specify the location of the point
a) in Cartesian coordinates, and
b) in spherical coordinates.
a) in Cartesian coordinates, and
b) in spherical coordinates.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
57
Determine wether the following vector fields are irrotational, solenoidal, both, or neither:
a) A = a x xy a y y 2 + a z xz,
b) B = r ( a r sin + a 2 cos ) ,
c) C = a x x a y 2 y + a z z,
d) D = a R k/R.
a) A = a x xy a y y 2 + a z xz,
b) B = r ( a r sin + a 2 cos ) ,
c) C = a x x a y 2 y + a z z,
d) D = a R k/R.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck



