Deck 14: Sorting and Searching

Question 1

Which of the following completes the selection sort method minimumPosition()?
A.if (a[i] > a[minPos]) { minPos = i; }
B.if (a[i] < a[j]) { minPos = i; }
C.if (a[i] < a[minPos]) { minPos = i; }
D.if (a[i] < a[minPos]) { i = minPos; }

Answer 1

if (a[i] < a[minPos]) { minPos = i; }

Question 2

In each iteration, selection sort places which element in the correct location?
A.The smallest in the array.
B.The largest element in the array.
C.A random element.
D.The smallest element not yet placed in prior iterations.

Answer 2

The smallest element not yet placed in prior iterations.

Question 3

Consider the sort method shown below for selection sort: Suppose we modify the loop condition to read i < a.length.What would be the result?
A.The sort would work exactly the same as before the code modification.
B.The sort would work, but run one more iteration.
C.The sort would work but with one less iteration.
D.An exception would occur.

Answer 3

The sort would work, but run one more iteration.

Question 4

The largestPosition method below returns the index of the largest element in the tail range of an array of integers.Select the expression that would be needed to complete the selectionSort method below, so that it sorts the elements in descending order.
A.(int i = 0; i < a.length - 1; i++)
B.(int i = a.length - 1; i > 0; i--)
C.(int i = a.length; i > 0; i--)
D.(int i = 0; i < a.length; i++)

Question 5

Consider the sort method shown below for selection sort: Suppose we modify the call to the swap method call to read swap(i, minPos).What would be the result?
A.An exception would occur.
B.The sort would produce incorrect results.
C.The sort would produce correct results.
D.The sort would work, but sort backwards.

Question 6

The code segment below is designed to add the elements in an array of integers.Select the expression needed to complete the code segment so that it calculates the elapsed running time.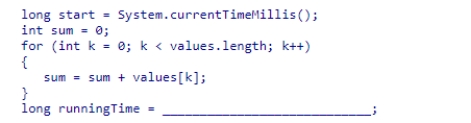
A.System.currentTimeMillis() - start
B.System.currentTimeMillis() + start
C.System.currentTimeMillis()
D.runningTime + start - System.currentTimeMillis()

Question 7

Consider the minimumPosition method from the SelectionSorter class.Complete the code to write a maximumPosition method that returns the index of the largest element in the range from index from to the end of the array.
A.if(a[i] == a[maxPos]) { maxPos = i; }
B.if(a[i] <= a[maxPos]) { maxPos = i; }
C.if(a[i] > a[maxPos]) { maxPos = i; }
D.if(a[i] < a[maxPos]) { maxPos = i; }

Question 8

The performance of an algorithm is most closely related to what?
A.The type of elements
B.The total number of elements
C.The total number of element visits
D.The number of lines of code in the method

Question 9

Consider the sort method for selection sort shown below: 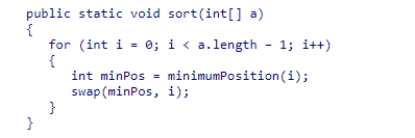Suppose we modify the loop control to read int i = 1; i < a.length - 1; i++.What would be the result?
A.The sort would still work correctly.
B.The sort would not consider the first array element.
C.An exception would occur
D.The sort would not consider the last array element.

Question 10

Consider the swap method shown below from the SelectionSorter class.If we modified it as shown in the swap2 method shown below, what would be the effect on the sort method?
A.Some array elements would be overwritten.
B.It would sort the array in reverse order.
C.It would still be correct, but run a little faster.
D.There would be no effect.

Question 11

What type of algorithm places elements in order?
A.deletion
B.searching
C.sorting
D.insertion

Question 12

What is the smallest value of n for which n2> 3n + 4?
A.6
B.5
C.4
D.3

Question 13

Suppose an algorithm requires a total of 3n3 + 2n2 - 3n + 4 visits.In big-Oh notation, the total number of visits is of what order?
A.n2 * n2
B.n2
C.n3
D.n6

Question 14

How large does n need to be so 0.3n2 is greater than 2.5n - 3?
A.9
B.5
C.7
D.3

Question 15

If you increase the size of a dataset fivefold, how much longer does it take to sort it with the selection sort algorithm?
A.Approximately 100 times longer
B.Approximately 5 times longer
C.Approximately 20 times longer
D.Approximately 25 times longer

Question 16

In big-Oh notation, suppose an algorithm requires an order of n3 element visits.How does doubling the number of elements affect the number of visits?
A.It number of visits goes up by a factor of eight.
B.It triples the number of visits.
C.It quadruples the number of visits.
D.It doubles the number of visits.

Question 17

Consider an array with n elements.If we visit each element n times, how many total visits will there be?
A.nn
B.n
C.2n
D.n2

Question 18

In big-Oh notation, when we consider the order of the number of visits an algorithm makes, what do we ignore?
I power of two terms
II the coefficients of the terms
III all lower order terms
A.II and III only
B.II only
C.I and II only
D.I only

Question 19

After 9 iterations of selection sort working on an array of 10 elements, what must hold true?
A.The largest element is correctly placed by default.
B.The largest element is incorrectly placed.
C.One more iteration is needed to complete the sort.
D.The smallest element is incorrectly placed.

Question 20

Suppose an array has n elements.We visit element #1 one time, element #2 two times, element #3 three times, and so forth.How many total visits will there be?
A.n2
B.n3
C.n(n+1)/2
D.2n

Question 21

How many comparisons does selection sort make when sorting an array of length n?
A.log(2n)
B.n
C.n( n + 1) / 2
D.n

Question 22

When the size of an array increases by a factor of 100, the time required by selection sort increases by a factor of ____.
A.5,000
B.10,000
C.12,000
D.2,000

Question 23

Merge sort is a(n) ____ algorithm.
A.O(log n)
B.O(n log(n))
C.O(n2)
D.O(n)

Question 24

In Big-Oh notation, selection sort is a(n) ____ algorithm.
A.O(1)
B.O(n2)
C.O(log n2)
D.log n

Question 25

The number of element visits for merge sort totals n + 5n log2 n.Which of the following is the appropriate big-Oh notation for merge sort?
A.n log2 n
B.n+ log2 n
C.n+ 5n
D.5n log2 n

Question 26

Consider the following code snippet: What sort algorithm is used in this code?
A.quicksort
B.insertion sort
C.merge sort
D.selection sort

Question 27

What is the worst-case performance of insertion sort?
A.O(log (n))
B.O(n2)
C.O(n)
D.O(n log (n))

Question 28

The merge sort algorithm presented in section 14.4, which sorts an array of integers in ascending order, uses the merge method which is partially shown below.Select the condition that would be needed to complete the method so that the elements are sorted in descending order.
A.first[iFirst] > second[iSecond]
B.first[iFirst] < second[iSecond]
C.iFirst > iSecond
D.iFirst < iSecond

Question 29

Which function has a faster growth rate: θ(n1/2) or θ(log(n))?
A.θ(n1/2)
B.θ(log(n))
C.They can't be compared.
D.They are the same.

Question 30

Find the simplest order of growth of the following expression: (n3 + n + 3)2.
A.θ(2n)
B.θ(n9)
C.θ(n5)
D.θ(n6)

Question 31

Which sort algorithm starts with an initial sequence of size 1, which is assumed to be sorted, and increases the size of the sorted sequence in the array in each iteration?
A.selection sort
B.quicksort
C.merge sort
D.insertion sort

Question 32

Choose the order of the following growth rates, from slowest to fastest: θ(n3), θ(nlog(n)), θ(n3/2), θ(2n).
A.θ(n log(n)), θ(n3/2), θ(n3), θ(2n)
B.θ(n3), θ(n log(n)), θ(n3/2), θ(2n)
C.θ(n3/2), θ(n log(n)), θ(n3), θ(2n)
D.θ(2n), θ(n3), θ(n3/2), θ(n log(n))

Question 33

Which sort algorithm starts by cutting the array in half and then recursively sorts each half?
A.insertion sort
B.quicksort
C.merge sort
D.selection sort

Question 34

Selection sort has O(n2) complexity.If a computer can sort 1,000 elements in 4 seconds, approximately how many seconds will it take the computer to sort 1,000 times that many, or 1,000,000 elements?
A.4,000,000
B.1,000,000
C.1,000
D.16

Question 35

If the array is already sorted, what is the performance of insertion sort?
A.O(log n)
B.O(n2)
C.O(n log n)
D.O(n)

Question 36

How many times can an array with 4,096 elements be cut into two equal pieces?
A.10
B.8
C.16
D.12

Question 37

Which notation, big-Oh, theta, or omega describes the growth rate of a function?
I big-Oh
II theta
III omega
A.II and III only
B.I only
C.I and II only
D.I, II, and III

Question 38

Find the simplest order of growth of the following expression: n3 + log(n5).
A.θ(log(n5))
B.θ(n3+ log(n))
C.θ(n+ log(n))
D.θ(n3)

Question 39

In general, the expression ____ means that f grows no faster than g.
A.f(n) = log g
B.f(n) = log g2
C.g(n) = O(f(n))
D.f(n) = O(g(n))

Question 40

Merge sort has a O(n log2(n)) complexity.If a computer can sort 1,024 elements in an amount of time x, approximately how long will it take the computer to sort 1,024 times that many, or 1,048,576 elements?
A.8,192x
B.1,024x
C.2,048x
D.1,048,576x

Question 41

Which sort algorithm is used in the sort method in the Java Arrays class when the array length is less than 7?
A.merge sort
B.quicksort
C.selection sort
D.insertion sort

Question 42

In the worst case, a linear search locates a value in an array of length n in ____ steps.
A.O(log n2)
B.O(n)
C.O(log n)
D.O(n2)

Question 43

Assume we are using quicksort to sort an array in ascending order.Into which array location does quicksort's strategy place a pivot element after partitioning?
A.closer to its correct final location
B.lowest index in array still available
C.its final correct location
D.highest index in array still available

Question 44

Given an ordered array with 15 elements, how many elements must be visited in the worst case of binary search?
A.2
B.8
C.4
D.3

Question 45

Given an ordered array with 31 elements, how many elements must be visited in the worst case of binary search?
A.16
B.8
C.5
D.4

Question 46

Which sort algorithm starts by partitioning the array and selecting a pivot element?
A.insertion sort
B.quicksort
C.merge sort
D.selection sort

Question 47

The following code is an example of a ___ search.
A.binary
B.sorted
C.linear
D.random

Question 48

If an element is present in an array of length n, how many element visits, on average, are necessary to find it using a linear search?
A.n / 2
B.2n
C.n
D.n2

Question 49

Assume we are using quicksort to sort an array in ascending order.What can we conclude about the elements to the left of the currently placed pivot element?
A.They are all less than or equal to the pivot element.
B.They are all greater than or equal to the pivot element.
C.They are all sorted.
D.None can equal the pivot element.

Question 50

The analysis for the number of visits in a binary search begins with the equation,
T(n) = T(n / 2) + 1.What does the number 1 represent in this equation?
A.The fact that the number of elements is odd.
B.The total number of recursions required.
C.The fact that we search either the left half or the right half, but not both.
D.One element visit before a recursive call on one half of the array.

Question 51

Which of the sorts in the textbook can be characterized by the fact that even in the worst case the running time will be O(n log(n)))?
I quicksort
II selection sort
III merge sort
A.I and III only
B.I only
C.II only
D.III only

Question 52

Suppose we are using binary search on an array with approximately 1,000,000 elements.How many visits should we expect to make in the worst case?
A.16
B.30
C.20
D.1

Question 53

Another name for linear search is ____ search.
A.random
B.sequential
C.sorted
D.binary

Question 54

Which of the sorts in the textbook are based on the strategy of divide and conquer?
I quicksort
II mergesort
III insertion sort
A.III only
B.I and II only
C.II only
D.I only

Question 55

Binary search is an ____ algorithm.
A.O(log n)
B.O(n2)
C.O(n log n)
D.O(n)

Question 56

When does quicksort's worst-case run-time behavior occur?
I when the data is randomly initialized in the array
II when the data is in ascending order
III when the data is in descending order
A.III only
B.I only
C.II only
D.II and III only

Question 57

If an element is present in an array of length n, how many element visits, in the worst case, are necessary to find it using a linear search?
A.n
B.2n
C.n / 2
D.n2

Question 58

Which of the sorts in the textbook can be characterized by the fact that the best case will have a running time of θ(n) if the data is already sorted?
I quicksort
II selection sort
III insertion sort
A.III only
B.II only
C.I only
D.I and III only

Question 59

In the worst case, quicksort is a(n) ____ algorithm.
A.O(log(n))
B.O(n2)
C.O(n log n)
D.O(n)

Question 60

A version of which sort algorithm is used in the sort method in the Java Arrays class?
A.merge sort
B.insertion sort
C.quicksort
D.selection sort

Question 61

The sort method of the Arrays class sorts arrays containing objects of classes that implement the ____ interface.
A.Ordered
B.Sortable
C.Array
D.Comparable

Question 62

The code segment below displays a pattern of asterisks.Select an expression to complete the code segment so that the resulting algorithm has O(n) running time.
A.(int j = n; j > 0; j = j / 2)
B.(int j = 1; j <= 10; j++)
C.(int j = 1; j < k; j++)
D.(int j = n; j > 0; j--)

Question 63

Assume that names is an array of String objects that has been initialized with a large number of elements.Select the statement that would sort the elements in names in ascending alphabetic order.
A.Collections.sort(names);
B.Arrays.sort(names, 0, names.length - 1);
C.Arrays.sort(names);
D.Collections.sort(names, 0, names.length - 1);

Question 64

An algorithm that cuts the work in half in each step is an ____ algorithm.
A.O(log (n))
B.O(n log (n))
C.O(n2)
D.O(n)

Question 65

A portion of your program implements a loop over n elements in which each step contains a fixed number of actions.What can you conclude about the running time of this section of code?
A.Its running time will be O(n2).
B.Its running time will be O(log (n)).
C.Its running time will be O(n log (n)).
D.Its running time will be O(n).

Question 66

A portion of your program includes the method shown in the code snippet below to examine the elements of an array arr: 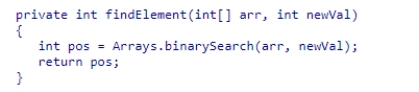What can you conclude about the running time of this section of code?
A.Its running time will be O(log (n)).
B.Its running time will be O(n).
C.Its running time will be O(n log (n)).
D.Its running time will be O(n2).

Question 67

The partial binary search method below is designed to search an array of String objects sorted in ascending order.Select the expression that would be needed to complete the method.
A.a[low].compareTo(item)
B.item.compareTo(a[mid])
C.item.equals(a[mid])
D.a[mid].compareTo(item)

Question 68

Can you search the following array using binary search?
int[] A = {6, 5, 4, 2, 0, 1, -1, -17};
A.No, negative numbers are not allowed because they indicate that a value is not present.
B.Yes.Binary search can be applied to any array.
C.No.Binary search can be applied to a sorted array only.
D.Yes, but the algorithm runs slower because the array is in descending order.

Question 69

Assume that bands is an ArrayList of String objects, which contains a number of elements in ascending order.Select a statement to complete the code segment below, which invokes the Java library binarySearch method to search for the string "Beatles".If the list does not already contain the string, it should be inserted in an appropriate location so that the list remains sorted.
A.bands.add(-1 * index, "Beatles");
B.bands.add(-1 - index, "Beatles");
C.bands.add(-1 * index + 1, "Beatles");
D.bands.add(index + 1, "Beatles");

Question 70

Which of the following statements about running times of algorithms is correct?
A.When determining the running time, lower-order terms must be taken into consideration.
B.When determining the running time, constants are not taken into consideration.
C.An algorithm that is O(1) means that only one comparison takes place.
D.An algorithm that is O(n) means that the number of comparisons does not grow as the size of the array increases.

Question 71

A portion of your program includes the loop shown in the code snippet below to examine the elements of an array arr: What can you conclude about the running time of this section of code?
A.Its running time will be O(n log (n)).
B.Its running time will be O(n2).
C.Its running time will be O(n).
D.Its running time will be O(log (n)).

Question 72

The partial linear search method below is designed to search an array of String objects.Select the expression that would be needed to complete the method.
A.a[i] == item
B.a[i].compareTo(item)
C.a[i].equals(item)
D.a[i].indexOf(item)

Question 73

A binary search is generally ____ a linear search.
A.faster than
B.less efficient than
C.slower than
D.equal to

Question 74

The method checkArray examines an array arr: What can you conclude about the running time of this section of code?
A.Its running time will be O(1).
B.Its running time will be O(n).
C.Its running time will be O(log (n)).
D.Its running time will be O(n2).

Question 75

A search technique where, in each step, you split the size of the search in half is called a____ search.
A.random
B.merging
C.linear
D.binary

Question 76

The code segment below prints some of the elements in an array with size n.Select an expression to complete the code segment so that the resulting algorithm has O(log n) running time.
A.(int j = 0; j < array.length; j = j + 2)
B.(int j = 0; j < array.length / 2; j++)
C.(int j = 1; j < array.length; j = j * 2)
D.(int j = 0; j < array.length; j++)

Question 77

An algorithm that tests whether the first array element is equal to any of the other array elements would be an ____ algorithm.
A.O(n log (n))
B.O(log (n))
C.O(1)
D.O(n)

Question 78

A portion of your program includes the loops shown in the code snippet below to examine the elements of two arrays, arr1 and arr2, both of length n: What can you conclude about the running time of this section of code?
A.Its running time will be O(log (n)).
B.Its running time will be O(n).
C.Its running time will be O(n log (n)).
D.Its running time will be O(n2).

Question 79

The code segment below displays a table of numbers.Select an expression to complete the code segment, so that the resulting algorithm has O(n2) running time.
A.(int j = 1; j <= 200; j++)
B.(int j = 1; j < k; j = j * 2)
C.(int j = 0; j < k; j++)
D.(int j = n; j > 0; j = j / 2)

Question 80

The method findLargest examines the elements of an array arr which contains non-negative values What can you conclude about the running time of this section of code?
A.Its running time will be O(n2).
B.Its running time will be O(n).
C.Its running time will be O(log (n)).
D.Its running time will be O(n log (n)).