Deck 15: Estimation of Dynamic Causal Effects
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/16
Play
Full screen (f)
Deck 15: Estimation of Dynamic Causal Effects
1
Suppose that a distributed lag regression is estimated, where the dependent variable is Y t instead of Y t. Explain how you would compute the dynamic multipliers of X t on Y t..
If a regression is run for 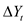 then the coefficients on independent variables X are multipliers of Y t. The cumulative dynamic multiplier is just the sum of the coefficients on X and the lagged terms of X.
then the coefficients on independent variables X are multipliers of Y t. The cumulative dynamic multiplier is just the sum of the coefficients on X and the lagged terms of X.
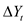 then the coefficients on independent variables X are multipliers of Y t. The cumulative dynamic multiplier is just the sum of the coefficients on X and the lagged terms of X.
then the coefficients on independent variables X are multipliers of Y t. The cumulative dynamic multiplier is just the sum of the coefficients on X and the lagged terms of X. 2
Suppose that oil prices are strictly exogenous. Discuss how you could improve on the estimates of the dynamic multipliers in Exercise 15.1.
Exercise
Increases in oil prices have been blamed for several recessions in developed countries. To quantify the effect of oil prices on real economic activity, researchers have done regressions like those discussed in this chapter. Let GDP t denote the value of quarterly gross domestic product in the United States and let Y t =(Q\n(GDP t / GDP t-1 ) be the quarterly percentage change in GDP. James Hamilton, an econometrician and macroeconomist, has suggested that oil prices adversely affect that economy only when they jump above their values in the recent past. Specifically, let O, equal the greater of zero or the percentage point difference between oil prices at date t and their maximum value during the past year. A distributed lag regression relating Y t and O t estimated over 1955:1-2000:IV, is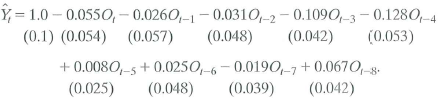
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+1 = O t+2 = … = 0). What is the predicted effect on output growth for each quarter over the next 2 years
b. Construct a 95% confidence interval for your answers in (a)..
c. What is the predicted cumulative change in GDP growth over eight quarters .
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 3.49. Are the coefficients significantly different from zero
Exercise
Increases in oil prices have been blamed for several recessions in developed countries. To quantify the effect of oil prices on real economic activity, researchers have done regressions like those discussed in this chapter. Let GDP t denote the value of quarterly gross domestic product in the United States and let Y t =(Q\n(GDP t / GDP t-1 ) be the quarterly percentage change in GDP. James Hamilton, an econometrician and macroeconomist, has suggested that oil prices adversely affect that economy only when they jump above their values in the recent past. Specifically, let O, equal the greater of zero or the percentage point difference between oil prices at date t and their maximum value during the past year. A distributed lag regression relating Y t and O t estimated over 1955:1-2000:IV, is
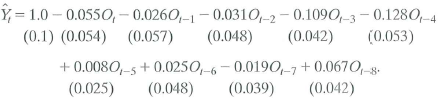
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+1 = O t+2 = … = 0). What is the predicted effect on output growth for each quarter over the next 2 years
b. Construct a 95% confidence interval for your answers in (a)..
c. What is the predicted cumulative change in GDP growth over eight quarters .
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 3.49. Are the coefficients significantly different from zero
If the independent variables are exogenous then OLS or GLS estimation can be applied for distributed lag models. GLS estimation is more efficient for large time observations.
3
Suppose that you added FDD t+1 as an additional regressor in Equation (15.2). If FDD is strictly exogenous, would you expect the coefficient on FDD t+1 to be zero or nonzero Would your answer change if FDD is exogenous but ilot strictly exogenous 

If the independent variable is strictly exogenous then a future outcome X t+1 will not have any effect on current error term u t this means that a distributed lag equation will have not X t+1 as a variable. In fact, it won't have any future outcomes as a variable.
If the independent variable is not strictly exogenous, then current error term may be explained by future X variables. Hence it may have non-zero coefficient for X t+1.
If the independent variable is not strictly exogenous, then current error term may be explained by future X variables. Hence it may have non-zero coefficient for X t+1.
4
Derive Equation (15.7) from Equation (15.4) and show that 0 = 0 , 1 = 1 , 2 = 1 + , 3 = 1 + 1 + 3 (etc.). 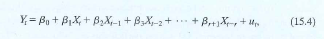
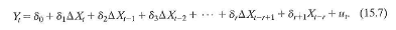
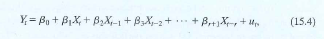
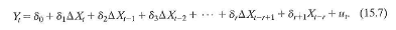

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the regression model Y t = 0 + 1 X t + u t where u, follows the stationary AR(1) mode with 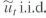 . with mean 0 and variance and |
. with mean 0 and variance and |
1 | 1, the regressor X t follows the stationary AR(1) mode with e t i.i.d. with mean 0 and variance and | 1 | 1, and e t is independent of for all t and i.
a. Show that var and var( X t ) = .
.
b. Show that cov and cov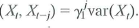 .
.
c. Show that corr and corr .
.
d. Consider the terms and f T in Equation (15.14).
i. Show that where is the variance of X and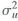 , is the variance of u.
, is the variance of u.
ii. Derive an expression for f
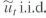 . with mean 0 and variance and |
. with mean 0 and variance and |1 | 1, the regressor X t follows the stationary AR(1) mode with e t i.i.d. with mean 0 and variance and | 1 | 1, and e t is independent of for all t and i.
a. Show that var and var( X t ) =
 .
.b. Show that cov and cov
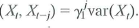 .
.c. Show that corr and corr
 .
.d. Consider the terms and f T in Equation (15.14).
i. Show that where is the variance of X and
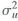 , is the variance of u.
, is the variance of u. ii. Derive an expression for f

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the regression model where u t follows the stationary AR(1) model 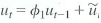 , with
, with  , i.i.d. with mean 0 and variance
, i.i.d. with mean 0 and variance 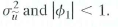
a. Suppose that X t is independent of for all t and j. Is X t exogenous (past and present) Is X t strictly exogenous (past, present, and future) .
b. Suppose that Is X t exogenous Is X t strictly exogenous
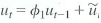 , with
, with  , i.i.d. with mean 0 and variance
, i.i.d. with mean 0 and variance 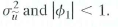
a. Suppose that X t is independent of for all t and j. Is X t exogenous (past and present) Is X t strictly exogenous (past, present, and future) .
b. Suppose that Is X t exogenous Is X t strictly exogenous

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the model in Exercise 15.7 with 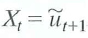
a. Is the OLS estimator of 1 consistent Explain..
b. Explain why the GLS estimator of 1 is not consistent..
c. Show that the infeasible GLS estimator
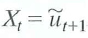
a. Is the OLS estimator of 1 consistent Explain..
b. Explain why the GLS estimator of 1 is not consistent..
c. Show that the infeasible GLS estimator

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the "constant-term-only" regression model Y₁ = 0 + u 1 where u follows the stationary AR(1) model 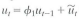 0 and variance
0 and variance  .
.
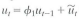 0 and variance
0 and variance  .
.
Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the ADL model is strictly exogenous.
a. Derive the impact effect of X on Y.
b. Derive the first five dynamic multipliers..
c. Derive the first five cumulative multipliers..
d. Derive the long-run cumulative dynamic multiplier.
a. Derive the impact effect of X on Y.
b. Derive the first five dynamic multipliers..
c. Derive the first five cumulative multipliers..
d. Derive the long-run cumulative dynamic multiplier.

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
10
Increases in oil prices have been blamed for several recessions in developed countries. To quantify the effect of oil prices on real economic activity, researchers have done regressions like those discussed in this chapter. Let GDP t denote the value of quarterly gross domestic product in the United States and let Y t =(Q\n(GDP t / GDP t-1 ) be the quarterly percentage change in GDP. James Hamilton, an econometrician and macroeconomist, has suggested that oil prices adversely affect that economy only when they jump above their values in the recent past. Specifically, let O, equal the greater of zero or the percentage point difference between oil prices at date t and their maximum value during the past year. A distributed lag regression relating Y t and O t estimated over 1955:1-2000:IV, is 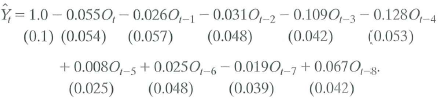
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+1 = O t+2 = … = 0). What is the predicted effect on output growth for each quarter over the next 2 years
b. Construct a 95% confidence interval for your answers in (a).
c. What is the predicted cumulative change in GDP growth over eight quarters
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 3.49. Are the coefficients significantly different from zero
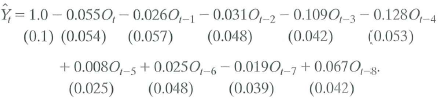
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+1 = O t+2 = … = 0). What is the predicted effect on output growth for each quarter over the next 2 years
b. Construct a 95% confidence interval for your answers in (a).
c. What is the predicted cumulative change in GDP growth over eight quarters
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 3.49. Are the coefficients significantly different from zero

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
11
In this exercise you will estimate the effect of oil prices on macroeconomic activity using monthly data on the Index of Industrial Production (IP) and the monthly measure of O, described in Exercise 15.1. The data can be found on the textbook Web site www.pearsonhighered.com/stock_watson in the file USMacroJVlonthly.
a. Compute the monthly growth rate in IP expressed in percentage points, What are the mean and standard deviation of ip_growth over the 1952:1-2009:12 sample period
b. Plot the value of O t Why are so many values of O t equal to zero Why aren't some values of O t negative
c. Estimate a distributed lag model of ip_growth onto current and 18 lagged values of O r What value of the HAC standard truncation parameter m did you choose Why
d. Taken as a group, are the coefficients on O t statistically significantly different from zero
e. Construct graphs like those in Figure 15.2 showing the estimated dynamic multipliers, cumulative multipliers, and 95% confidence intervals. Comment on the real-world size of the multipliers.
f. Suppose that high demand in the United States (evidenced by large values of ip_growth) leads to increases in oil prices. Is O i exogenous Are the estimated multipliers shown in the graphs in (e) reliable Explain.
Exercise
Increases in oil prices have been blamed for several recessions in developed countries. To quantify the effect of oil prices on real economic activity, researchers have done regressions like those discussed in this chapter. Let GDP t denote the value of quarterly gross domestic product in the United States and let Y t =(Q\n(GDP t / GDP t-1 ) be the quarterly percentage change in GDP. James Hamilton, an econometrician and macroeconomist, has suggested that oil prices adversely affect that economy only when they jump above their values in the recent past. Specifically, let O, equal the greater of zero or the percentage point difference between oil prices at date t and their maximum value during the past year. A distributed lag regression relating Y t and O t estimated over 1955:1-2000:IV, is
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+1 = O t+2 = … = 0). What is the predicted effect on output growth for each quarter over the next 2 years
b. Construct a 95% confidence interval for your answers in (a).
c. What is the predicted cumulative change in GDP growth over eight quarters
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 3.49. Are the coefficients significantly different from zero
a. Compute the monthly growth rate in IP expressed in percentage points, What are the mean and standard deviation of ip_growth over the 1952:1-2009:12 sample period
b. Plot the value of O t Why are so many values of O t equal to zero Why aren't some values of O t negative
c. Estimate a distributed lag model of ip_growth onto current and 18 lagged values of O r What value of the HAC standard truncation parameter m did you choose Why
d. Taken as a group, are the coefficients on O t statistically significantly different from zero
e. Construct graphs like those in Figure 15.2 showing the estimated dynamic multipliers, cumulative multipliers, and 95% confidence intervals. Comment on the real-world size of the multipliers.
f. Suppose that high demand in the United States (evidenced by large values of ip_growth) leads to increases in oil prices. Is O i exogenous Are the estimated multipliers shown in the graphs in (e) reliable Explain.
Exercise
Increases in oil prices have been blamed for several recessions in developed countries. To quantify the effect of oil prices on real economic activity, researchers have done regressions like those discussed in this chapter. Let GDP t denote the value of quarterly gross domestic product in the United States and let Y t =(Q\n(GDP t / GDP t-1 ) be the quarterly percentage change in GDP. James Hamilton, an econometrician and macroeconomist, has suggested that oil prices adversely affect that economy only when they jump above their values in the recent past. Specifically, let O, equal the greater of zero or the percentage point difference between oil prices at date t and their maximum value during the past year. A distributed lag regression relating Y t and O t estimated over 1955:1-2000:IV, is

a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+1 = O t+2 = … = 0). What is the predicted effect on output growth for each quarter over the next 2 years
b. Construct a 95% confidence interval for your answers in (a).
c. What is the predicted cumulative change in GDP growth over eight quarters
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 3.49. Are the coefficients significantly different from zero


Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
12
In the 1970s a common practice was to estimate a distributed lag model relating changes in nominal gross domestic product ( Y ) to current and past changes in the money supply ( X ). Under what assumptions will this regression estimate the causal effects of money on nominal GDP Are these assumptions likely to be satisfied in a modern economy like that of the United States

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
13
Macroeconomists have also noticed that interest rates change following oil price jumps. Let R t denote the interest rate on 3-month Treasury bills (in percentage points at an annual rate). The distributed lag regression relating the change in R t ( R t ) to O t estimated over 1955:1-2000:IV is 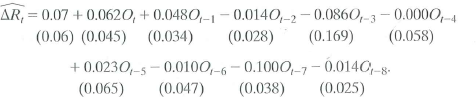
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+l = O t +2 = … = 0). What is the predicted change in interest rates for each quarter over the next 2 years
b. Construct 95% confidence intervals for your answers to (a).
c. What is the effect of this change in oil prices on the level of interest rates in period t + 8 How is your answer related to the cumulative multiplier
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 4.25. Are the coefficients significantly different from zero
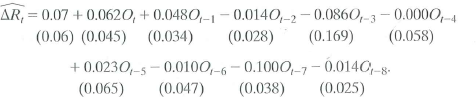
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+l = O t +2 = … = 0). What is the predicted change in interest rates for each quarter over the next 2 years
b. Construct 95% confidence intervals for your answers to (a).
c. What is the effect of this change in oil prices on the level of interest rates in period t + 8 How is your answer related to the cumulative multiplier
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 4.25. Are the coefficients significantly different from zero

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
14
In the data file USMacro_Monthly, you will find data on two aggregate price series for the United States: the Consumer Price Index (CPI) and the Personal Consumption Expenditures Deflator (PCED). These series are alternative measures of consumer prices in the United States. The CPI prices a basket of goods whose composition is updated every 5-10 years. The PCED uses chain-weighting to price a basket of goods whose composition changes from month to month. Economists have argued that the CPI will overstate inflation because it does not take into account the substitution that occurs when relative prices change. If this substitution bias is important, then average CPI inflation should be systematically higher than PCED inflation. Let 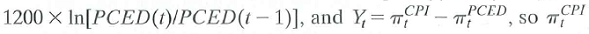 , is the monthly rate of price inflation (measured in percentage points at an annual rate) based on the CPI, is the monthly rate of price inflation from the PCED, and Y i is the difference. Using data from 1970:1 through 2009:12, carry out the following exercises.
, is the monthly rate of price inflation (measured in percentage points at an annual rate) based on the CPI, is the monthly rate of price inflation from the PCED, and Y i is the difference. Using data from 1970:1 through 2009:12, carry out the following exercises.
a. Compute the sample means of Are these point estimates consistent with the presence of economically significant substitution bias in the CPI
b. Compute the sample mean of Y t. Explain why it is numerically equal to the difference in the means computed in (a).
c. Show that the population mean of Y is equal to the difference of the population means of the two inflation rates.
d. Consider the "constant-term-only" regression: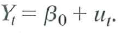 . Show that
. Show that  . Do you think that u, is serially correlated Explain.
. Do you think that u, is serially correlated Explain.
e. Construct a 95% confidence interval for 0. What value of the HAC standard truncation parameter m did you choose Why
f. Is there statistically significant evidence that the mean inflation rate for the CPI is greater than the rate for the PCED
g. Is there evidence of instability in 0 Carry out a QLR test.
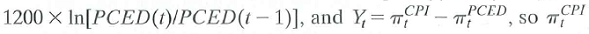 , is the monthly rate of price inflation (measured in percentage points at an annual rate) based on the CPI, is the monthly rate of price inflation from the PCED, and Y i is the difference. Using data from 1970:1 through 2009:12, carry out the following exercises.
, is the monthly rate of price inflation (measured in percentage points at an annual rate) based on the CPI, is the monthly rate of price inflation from the PCED, and Y i is the difference. Using data from 1970:1 through 2009:12, carry out the following exercises.a. Compute the sample means of Are these point estimates consistent with the presence of economically significant substitution bias in the CPI
b. Compute the sample mean of Y t. Explain why it is numerically equal to the difference in the means computed in (a).
c. Show that the population mean of Y is equal to the difference of the population means of the two inflation rates.
d. Consider the "constant-term-only" regression:
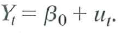 . Show that
. Show that  . Do you think that u, is serially correlated Explain.
. Do you think that u, is serially correlated Explain. e. Construct a 95% confidence interval for 0. What value of the HAC standard truncation parameter m did you choose Why
f. Is there statistically significant evidence that the mean inflation rate for the CPI is greater than the rate for the PCED
g. Is there evidence of instability in 0 Carry out a QLR test.

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose that X is strictly exogenous. A researcher estimates an ADL(1,1) model, calculates the regression residual, and finds the residual to be highly serially correlated. Should the researcher estimate a new ADL model with additional lags or simply use HAC standard errors for the ADL(1,1) estimated coefficients

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck
16
Consider two different randomized experiments. In experiment A, oil prices are set randomly and the central bank reacts according to its usual policy rules in response to economic conditions, including changes in the oil price. In experiment B, oil prices are set randomly and the central bank holds interest rates constant and in particular does not respond to the oil price changes. In both, GDP growth is observed. Now suppose that oil prices are exogenous in the regression in Exercise 15.1. To which experiment, A or B, does the dynamic causal effect estimated in Exercise 15.1 correspond
Exercise
Increases in oil prices have been blamed for several recessions in developed countries. To quantify the effect of oil prices on real economic activity, researchers have done regressions like those discussed in this chapter. Let GDP t denote the value of quarterly gross domestic product in the United States and let Y t =(Q\n(GDP t / GDP t-1 ) be the quarterly percentage change in GDP. James Hamilton, an econometrician and macroeconomist, has suggested that oil prices adversely affect that economy only when they jump above their values in the recent past. Specifically, let O, equal the greater of zero or the percentage point difference between oil prices at date t and their maximum value during the past year. A distributed lag regression relating Y t and O t estimated over 1955:1-2000:IV, is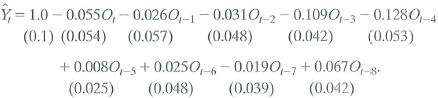
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+l = O t +2 = … = 0). What is the predicted change in interest rates for each quarter over the next 2 years
b. Construct 95% confidence intervals for your answers to (a).
c. What is the effect of this change in oil prices on the level of interest rates in period t + 8 How is your answer related to the cumulative multiplier
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 4.25. Are the coefficients significantly different from zero
Exercise
Increases in oil prices have been blamed for several recessions in developed countries. To quantify the effect of oil prices on real economic activity, researchers have done regressions like those discussed in this chapter. Let GDP t denote the value of quarterly gross domestic product in the United States and let Y t =(Q\n(GDP t / GDP t-1 ) be the quarterly percentage change in GDP. James Hamilton, an econometrician and macroeconomist, has suggested that oil prices adversely affect that economy only when they jump above their values in the recent past. Specifically, let O, equal the greater of zero or the percentage point difference between oil prices at date t and their maximum value during the past year. A distributed lag regression relating Y t and O t estimated over 1955:1-2000:IV, is
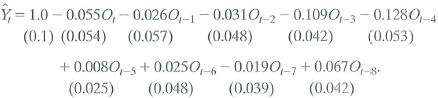
a. Suppose that oil prices jump 25% above their previous peak value and stay at this new higher level (so that O t = 25 and O t+l = O t +2 = … = 0). What is the predicted change in interest rates for each quarter over the next 2 years
b. Construct 95% confidence intervals for your answers to (a).
c. What is the effect of this change in oil prices on the level of interest rates in period t + 8 How is your answer related to the cumulative multiplier
d. The HAC F-statistic testing whether the coefficients on O t and its lags are zero is 4.25. Are the coefficients significantly different from zero

Unlock Deck
Unlock for access to all 16 flashcards in this deck.
Unlock Deck
k this deck



