Deck 10: Taylor Polynomials and Infinite Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/48
Play
Full screen (f)
Deck 10: Taylor Polynomials and Infinite Series
1
Find the nth-degree Taylor polynomial at the indicated value of a. Write the answer in expanded notation.
f(x) = e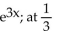
A)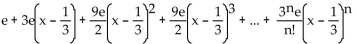
B)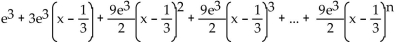
C)
D)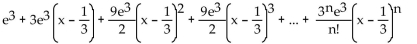
f(x) = e
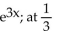
A)
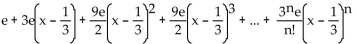
B)
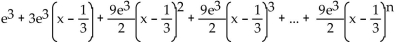
C)

D)
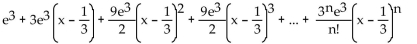
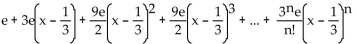
2
Solve the problem.
Over a portion of a battery's charge, the voltage delivered drops as the battery is discharged, according to the following equation: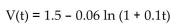 where t is the time in hours that the battery is being discharged. Use the second-degree Taylor polynomial for V(t) to
where t is the time in hours that the battery is being discharged. Use the second-degree Taylor polynomial for V(t) to
Find the average voltage over the first 5 hours.
A)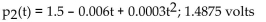
B)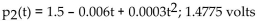
C)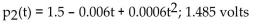
D)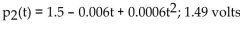
Over a portion of a battery's charge, the voltage delivered drops as the battery is discharged, according to the following equation:
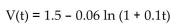 where t is the time in hours that the battery is being discharged. Use the second-degree Taylor polynomial for V(t) to
where t is the time in hours that the battery is being discharged. Use the second-degree Taylor polynomial for V(t) toFind the average voltage over the first 5 hours.
A)
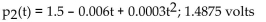
B)
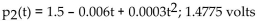
C)
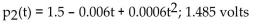
D)
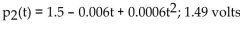
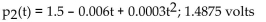
3
Find the indicated Taylor polynomial at 0.
 )
)
A)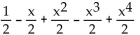
B)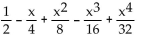
C)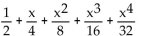
D)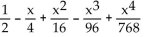
 )
)A)
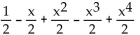
B)
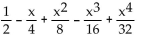
C)
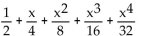
D)
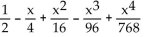
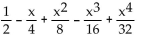
4
Find the nth-degree Taylor polynomial at 0 for f, find the Taylor series at 0 for f, and determine the values of x for which 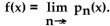
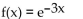
A)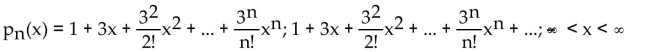
B)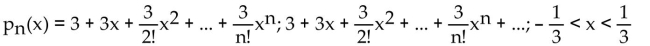
C)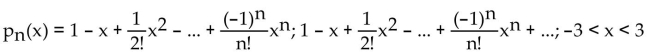
D)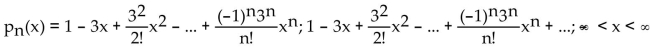
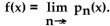
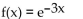
A)
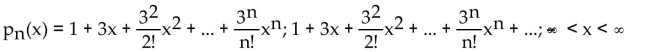
B)
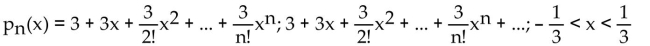
C)
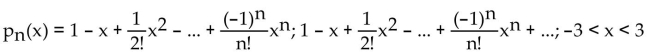
D)
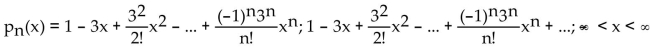

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
5
Use a Taylor polynomial of the indicated degree to approximate the function at the given value of x. Round to seven
decimal places.
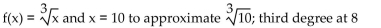
A)
B)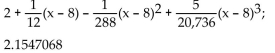
C)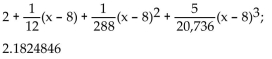
D)
decimal places.
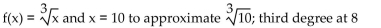
A)

B)
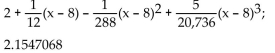
C)
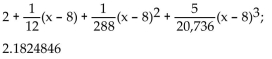
D)


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
6
Find f(4)(x).
f(x) = sin (x + 2)
A) 16 cos x
B) cos (x + 2)
C) 16 sin x
D) sin (x + 2)
f(x) = sin (x + 2)
A) 16 cos x
B) cos (x + 2)
C) 16 sin x
D) sin (x + 2)

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
7
Find the interval of convergence of the given Taylor series representation.
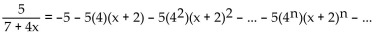
A)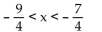
B)
C)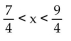
D) -3 < x < -1
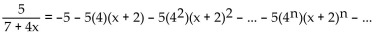
A)
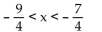
B)

C)
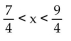
D) -3 < x < -1

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
8
Find f(n)(x).
f(x) =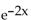
A)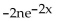
B)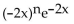
C)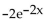
D)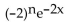
f(x) =
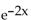
A)
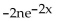
B)
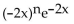
C)
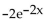
D)
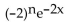

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
9
Find the nth-degree Taylor polynomial at 0. Write the answer in expanded notation.
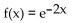
A)
B)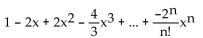
C)
D)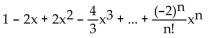
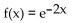
A)

B)
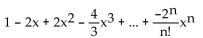
C)

D)

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
10
Find the nth-degree Taylor polynomial at 0 for f, find the Taylor series at 0 for f, and determine the values of x for which 
A)
B)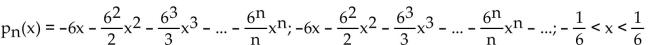
C)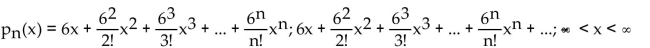
D)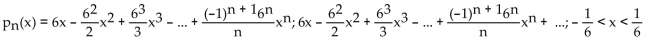
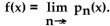
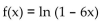
A)
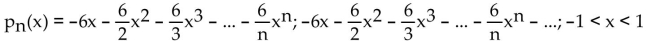
B)
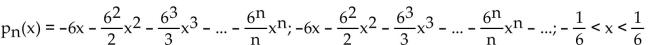
C)
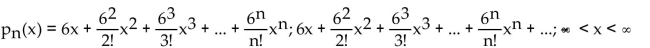
D)
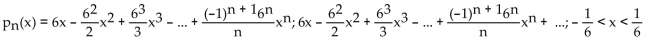

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the problem.
The downward velocity of a skydiver approaches a maximum value because of air resistance. The skydiver's velocity (in meters per second) can be modeled by the function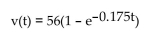 where t is the time seconds after jumping. Use the second-degree Taylor polynomial for v(t) at t = 0 to approximate
where t is the time seconds after jumping. Use the second-degree Taylor polynomial for v(t) at t = 0 to approximate
The distance fallen after 5 seconds.
A)
B)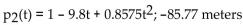
C)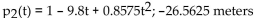
D)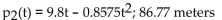
The downward velocity of a skydiver approaches a maximum value because of air resistance. The skydiver's velocity (in meters per second) can be modeled by the function
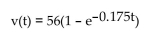 where t is the time seconds after jumping. Use the second-degree Taylor polynomial for v(t) at t = 0 to approximate
where t is the time seconds after jumping. Use the second-degree Taylor polynomial for v(t) at t = 0 to approximateThe distance fallen after 5 seconds.
A)

B)
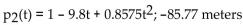
C)
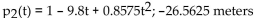
D)
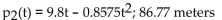

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
12
Find the indicated Taylor polynomial at 0.
f(x) =
A)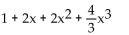
B)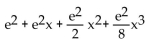
C)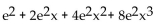
D)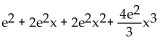
f(x) =

A)
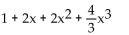
B)
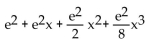
C)
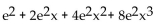
D)
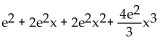

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
13
Find the interval of convergence of the given Taylor series representation.
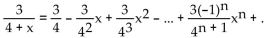 ..
..
A) -4 < x < 4
B) -3 < x < 3
C)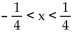
D) -1 < x < 1
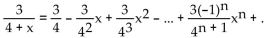 ..
..A) -4 < x < 4
B) -3 < x < 3
C)
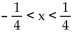
D) -1 < x < 1

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
14
Find the indicated Taylor polynomial at the given value of a.
sin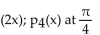
A)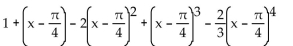
B)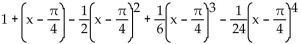
C)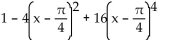
D)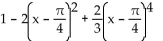
sin
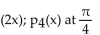
A)
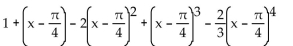
B)
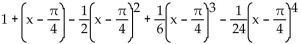
C)
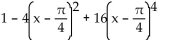
D)
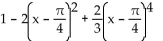

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
15
Find the nth-degree Taylor polynomial at the indicated value of a. Write the answer in expanded notation.
f(x) =
A)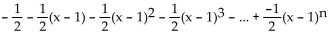
B)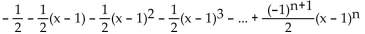
C)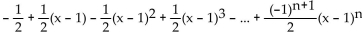
D)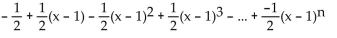
f(x) =

A)
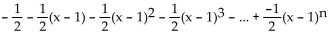
B)
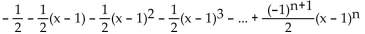
C)
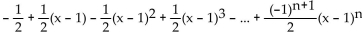
D)
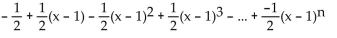

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
16
Use a Taylor polynomial of the indicated degree to approximate the function at the given value of x. Round to seven
decimal places.
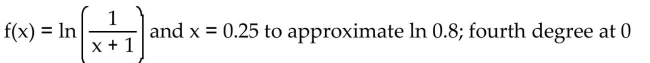
A)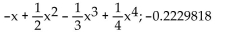
B)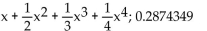
C)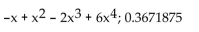
D)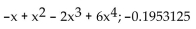
decimal places.
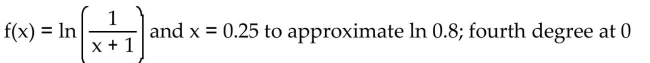
A)
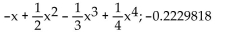
B)
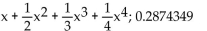
C)
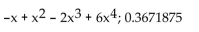
D)
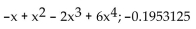

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
17
Find the indicated Taylor polynomial at the given value of a.
f(x) =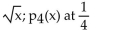
A)
B)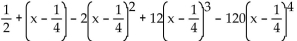
C)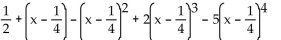
D)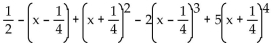
f(x) =
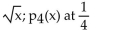
A)

B)
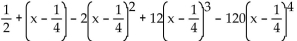
C)
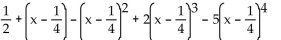
D)
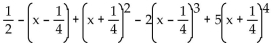

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
18
Find the nth-degree Taylor polynomial at 0. Write the answer in expanded notation.
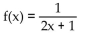
A)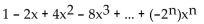
B)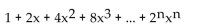
C)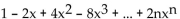
D)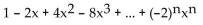
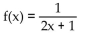
A)
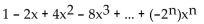
B)
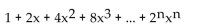
C)
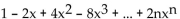
D)
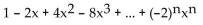

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the problem.
A train traveling over a hill whose height (in feet) above sea level is modeled by the equation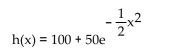 where x is the distance (in miles) from the center of the hill. Use the second-degree Taylor polynomial at x = 0 for h(x) to find the average height of the train as it crosses over the hill from 1 mile out to 1 mile past the center.
where x is the distance (in miles) from the center of the hill. Use the second-degree Taylor polynomial at x = 0 for h(x) to find the average height of the train as it crosses over the hill from 1 mile out to 1 mile past the center.
A)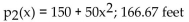
B)
C)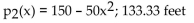
D)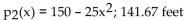
A train traveling over a hill whose height (in feet) above sea level is modeled by the equation
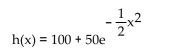 where x is the distance (in miles) from the center of the hill. Use the second-degree Taylor polynomial at x = 0 for h(x) to find the average height of the train as it crosses over the hill from 1 mile out to 1 mile past the center.
where x is the distance (in miles) from the center of the hill. Use the second-degree Taylor polynomial at x = 0 for h(x) to find the average height of the train as it crosses over the hill from 1 mile out to 1 mile past the center.A)
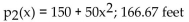
B)

C)
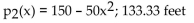
D)
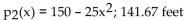

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
20
Find f(3)(x).
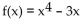
A) 4x
B) 24x
C) 4x - 3
D)
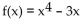
A) 4x
B) 24x
C) 4x - 3
D)


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
21
Find the Taylor series at 0. State the interval of convergence for the series.
ln (1 - x) + ln (1 + x)
A)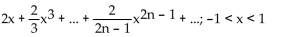
B)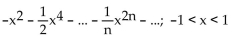
C)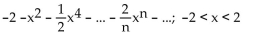
D)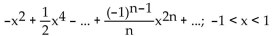
ln (1 - x) + ln (1 + x)
A)
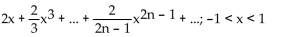
B)
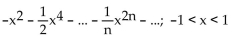
C)
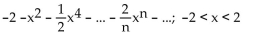
D)
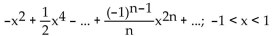

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
22
Use the substitution t = x - a to find the Taylor series at the indicated value of a. State the interval of convergence for the
series.
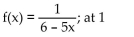
A)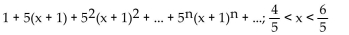
B)
C)
D)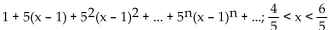
series.
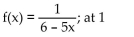
A)
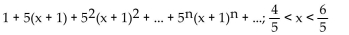
B)

C)

D)
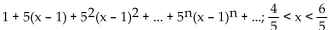

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the problem.
Find the Taylor polynomial of degree 2n at 0 for g(x) = cos x.
A)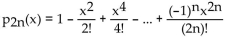
B)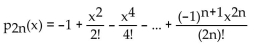
C)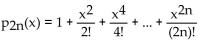
D)
Find the Taylor polynomial of degree 2n at 0 for g(x) = cos x.
A)
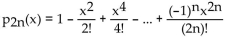
B)
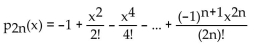
C)
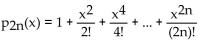
D)


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
24
Find the Taylor series at 0. State the interval of convergence for the series.
The Taylor series at 0 for the sine and cosine functions are given below. F(x) satisfies
F(x) satisfies 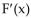 = sin x and F(0) = -3
= sin x and F(0) = -3
A)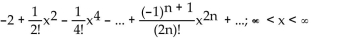
B)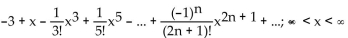
C)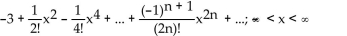
D)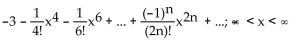
The Taylor series at 0 for the sine and cosine functions are given below.
 F(x) satisfies
F(x) satisfies 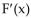 = sin x and F(0) = -3
= sin x and F(0) = -3A)
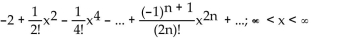
B)
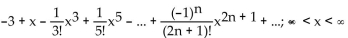
C)
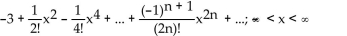
D)
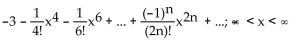

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
25
Find the nth-degree Taylor polynomial at the indicated value of a for f, find the Taylor series at a for f and determine the
values of x for which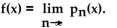
f(x) =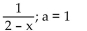
A)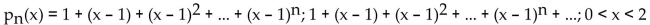
B)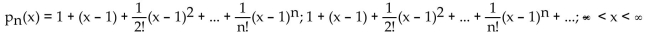
C)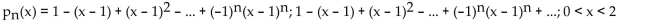
D)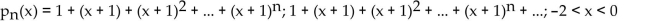
values of x for which
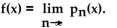
f(x) =
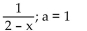
A)
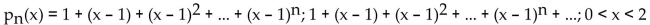
B)
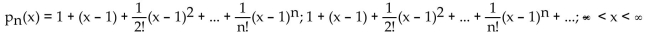
C)
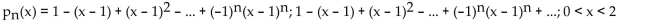
D)
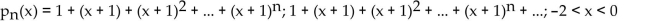

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
26
Find the Taylor series at 0. State the interval of convergence for the series.
f(x) satisfies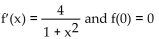
A)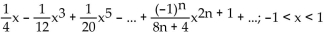
B)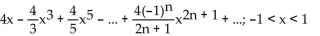
C)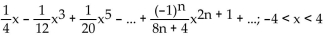
D)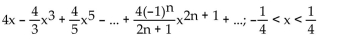
f(x) satisfies
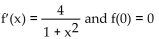
A)
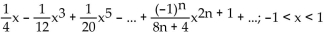
B)
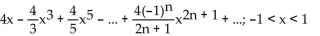
C)
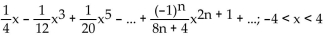
D)
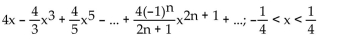

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
27
Use a Taylor polynomial at 0 to approximate the expression with an error of no more than 0.000005. Select the polynomial
of lowest degree that can be used to obtain this accuracy and state the degree of this polynomial. Round to six decimal
places.
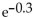
A) 0.740818; n = 6
B) 0.740838; n = 5
C) 0.740817; n = 4
D) 0.740817; n = 5
of lowest degree that can be used to obtain this accuracy and state the degree of this polynomial. Round to six decimal
places.
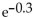
A) 0.740818; n = 6
B) 0.740838; n = 5
C) 0.740817; n = 4
D) 0.740817; n = 5

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
28
Find the Taylor series at 0. State the interval of convergence for the series.
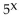
A)
B)
C)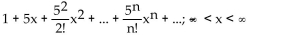
D)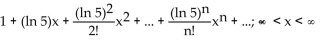
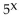
A)

B)

C)
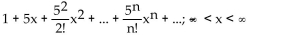
D)
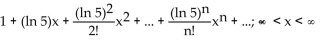

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
29
Find the Taylor series at 0. State the interval of convergence for the series.
f(x) satisfies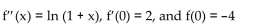
A)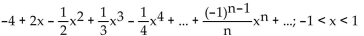
B)
C)
D)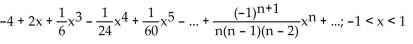
f(x) satisfies
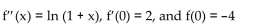
A)
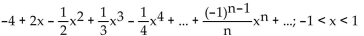
B)

C)

D)
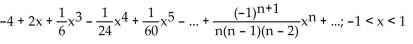

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
30
Find the Taylor series at 0. State the interval of convergence for the series.
 The Taylor series at 0 for the sine and cosine functions are given below.
The Taylor series at 0 for the sine and cosine functions are given below. 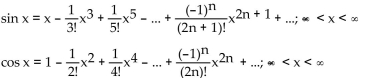
A)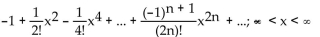
B)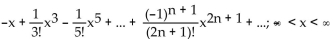
C)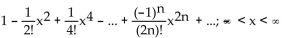
D)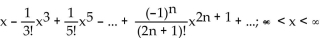
 The Taylor series at 0 for the sine and cosine functions are given below.
The Taylor series at 0 for the sine and cosine functions are given below. 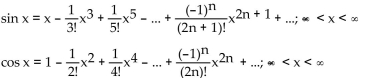
A)
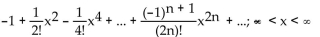
B)
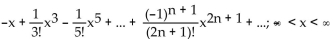
C)
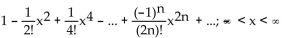
D)
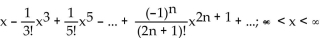

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.
Evaluating the Taylor series at 0 for f(x) = ln (1 + x) at x = 0.6 produces the following series. Use four terms in this series to approximate ln 1.6, and then estimate the error in this approximation.
Use four terms in this series to approximate ln 1.6, and then estimate the error in this approximation.
A)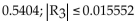
B)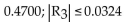
C)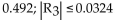
D)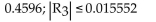
Evaluating the Taylor series at 0 for f(x) = ln (1 + x) at x = 0.6 produces the following series.
 Use four terms in this series to approximate ln 1.6, and then estimate the error in this approximation.
Use four terms in this series to approximate ln 1.6, and then estimate the error in this approximation.A)
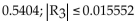
B)
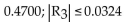
C)
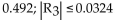
D)
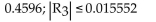

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
32
Use the substitution t = x - a to find the Taylor series at the indicated value of a. State the interval of convergence for the
series.
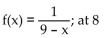
A)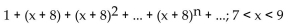
B)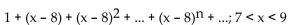
C)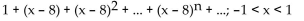
D)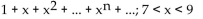
series.
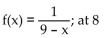
A)
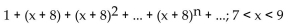
B)
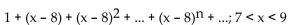
C)
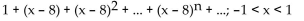
D)
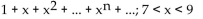

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
33
Find the nth-degree Taylor polynomial at the indicated value of a for f, find the Taylor series at a for f and determine the
values of x for which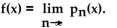
f(x) = ln (5 - x); a = 4
A)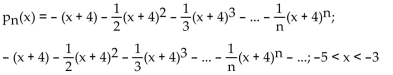
B)
C)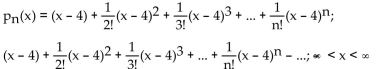
D)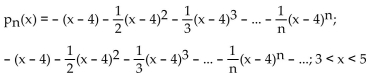
values of x for which
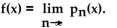
f(x) = ln (5 - x); a = 4
A)
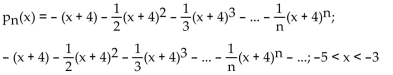
B)

C)
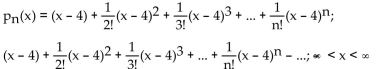
D)
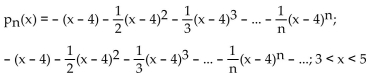

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
34
Use the third-degree Taylor polynomial at 0 for the given function to approximate the expression, and then estimate the
error in the approximation. Round to six decimal places as needed.
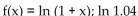
A)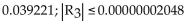
B)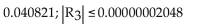
C)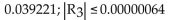
D)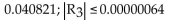
error in the approximation. Round to six decimal places as needed.
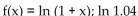
A)
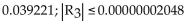
B)
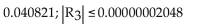
C)
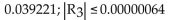
D)
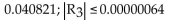

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
35
Use the third-degree Taylor polynomial at 0 for the given function to approximate the expression, and then estimate the
error in the approximation. Round to six decimal places as needed.
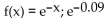
A)
B)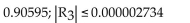
C)
D)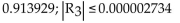
error in the approximation. Round to six decimal places as needed.
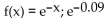
A)

B)
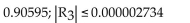
C)

D)

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
36
Find the Taylor series at 0. State the interval of convergence for the series.
 use the Taylor series at 0 for
use the Taylor series at 0 for 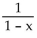 and repeated applications of the differentiation property of Taylor series
and repeated applications of the differentiation property of Taylor series
A)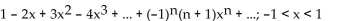
B)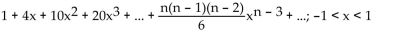
C)
D)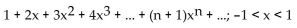
 use the Taylor series at 0 for
use the Taylor series at 0 for 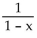 and repeated applications of the differentiation property of Taylor series
and repeated applications of the differentiation property of Taylor seriesA)
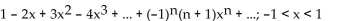
B)
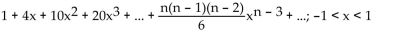
C)

D)
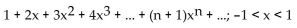

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the problem.
Evaluating the Taylor series at 0 for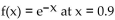 produces the following series.
produces the following series. 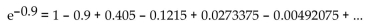 Use three terms in this series to approximate
Use three terms in this series to approximate 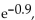 and then estimate the error in this approximation.
and then estimate the error in this approximation.
A)
B)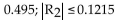
C)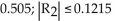
D)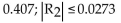
Evaluating the Taylor series at 0 for
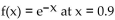 produces the following series.
produces the following series. 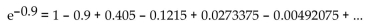 Use three terms in this series to approximate
Use three terms in this series to approximate 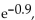 and then estimate the error in this approximation.
and then estimate the error in this approximation.A)

B)
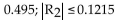
C)
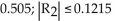
D)
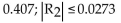

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
38
Find the Taylor series at 0. State the interval of convergence for the series.
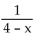
A)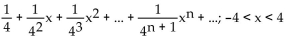
B)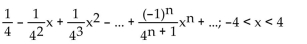
C)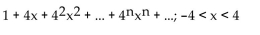
D)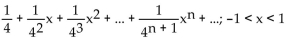
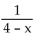
A)
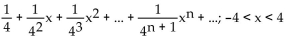
B)
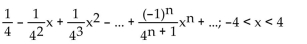
C)
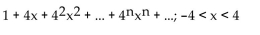
D)
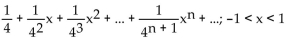

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the problem.
Find the Taylor series at 0 for g(x) = cos x (while evaluating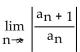 cannot be directly applied, other techniques can be used to show that the Taylor series at 0 for g(x) = cos x converges for all values of x).
cannot be directly applied, other techniques can be used to show that the Taylor series at 0 for g(x) = cos x converges for all values of x).
A)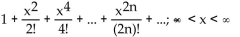
B)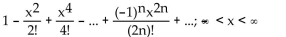
C)
D)
Find the Taylor series at 0 for g(x) = cos x (while evaluating
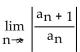 cannot be directly applied, other techniques can be used to show that the Taylor series at 0 for g(x) = cos x converges for all values of x).
cannot be directly applied, other techniques can be used to show that the Taylor series at 0 for g(x) = cos x converges for all values of x).A)
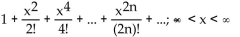
B)
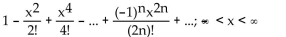
C)

D)


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
40
Find the Taylor series at 0. State the interval of convergence for the series.
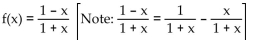
A)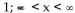
B)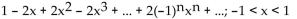
C)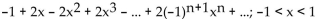
D)
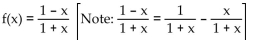
A)
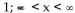
B)
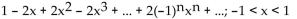
C)
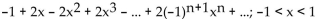
D)


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
Assume that f(x) is a function such that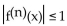 for all n and all x and let
for all n and all x and let 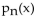 be the nth-degree Taylor polynomial for f at 0. Use Taylor's formula for the remainder to find the smallest value of n such that the error
be the nth-degree Taylor polynomial for f at 0. Use Taylor's formula for the remainder to find the smallest value of n such that the error
In the approximation of f(6) by pn(6) is guaranteed to be less than 0.001.
A) n = 20
B) n = 25
C) n = 6
D) n = 13
Assume that f(x) is a function such that
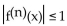 for all n and all x and let
for all n and all x and let 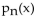 be the nth-degree Taylor polynomial for f at 0. Use Taylor's formula for the remainder to find the smallest value of n such that the error
be the nth-degree Taylor polynomial for f at 0. Use Taylor's formula for the remainder to find the smallest value of n such that the errorIn the approximation of f(6) by pn(6) is guaranteed to be less than 0.001.
A) n = 20
B) n = 25
C) n = 6
D) n = 13

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the problem. Use the theorem for error estimation for alternating series to perform the indicated error estimation.
Given the demand equation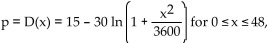 approximate the average price (in dollars) over the demand interval 0, 20 to within ± 0.005.
approximate the average price (in dollars) over the demand interval 0, 20 to within ± 0.005.
A) $13.924
B) $9.284
C) $0.716
D) $13.926
Given the demand equation
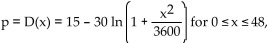 approximate the average price (in dollars) over the demand interval 0, 20 to within ± 0.005.
approximate the average price (in dollars) over the demand interval 0, 20 to within ± 0.005.A) $13.924
B) $9.284
C) $0.716
D) $13.926

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem. Use the theorem for error estimation for alternating series to perform the indicated error estimation.
The rate of healing for a skin wound (in square centimeters per day) is given by A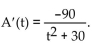 The initial wound has an area of 12 square centimeters. Use the second-degree Taylor polynomial at 0 for A‛(t) to
The initial wound has an area of 12 square centimeters. Use the second-degree Taylor polynomial at 0 for A‛(t) to
Approximate the area of the would after 3 days, and estimate the error in this approximation.
A)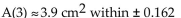
B)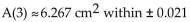
C)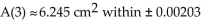
D)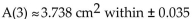
The rate of healing for a skin wound (in square centimeters per day) is given by A
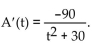 The initial wound has an area of 12 square centimeters. Use the second-degree Taylor polynomial at 0 for A‛(t) to
The initial wound has an area of 12 square centimeters. Use the second-degree Taylor polynomial at 0 for A‛(t) toApproximate the area of the would after 3 days, and estimate the error in this approximation.
A)
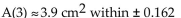
B)
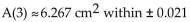
C)
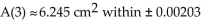
D)
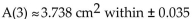

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem. Use the theorem for error estimation for alternating series to perform the indicated error estimation.
The income distribution for a certain country is represented by the Lorenz curve with the equation f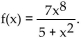 Approximate the index of income concentration to within ± 0.005.
Approximate the index of income concentration to within ± 0.005.
A) 0.740
B) 0.731
C) 0.733
D) 0.833
The income distribution for a certain country is represented by the Lorenz curve with the equation f
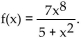 Approximate the index of income concentration to within ± 0.005.
Approximate the index of income concentration to within ± 0.005.A) 0.740
B) 0.731
C) 0.733
D) 0.833

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
45
Use a Taylor series at 0 to approximate the integral with an error of no more than 0.0005.
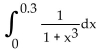
A) 0.2980
B) 0.3
C) 0.0020
D) 0.2979
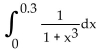
A) 0.2980
B) 0.3
C) 0.0020
D) 0.2979

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
46
Use a Taylor polynomial at 0 to approximate the expression with an error of no more than 0.000005. Select the polynomial
of lowest degree that can be used to obtain this accuracy and state the degree of this polynomial. Round to six decimal
places.
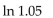
A) 0.048792; n = 3
B) 0.04875; n = 2
C) 0.048790; n = 3
D) 0.048790; n = 4
of lowest degree that can be used to obtain this accuracy and state the degree of this polynomial. Round to six decimal
places.
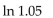
A) 0.048792; n = 3
B) 0.04875; n = 2
C) 0.048790; n = 3
D) 0.048790; n = 4

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
Use the second-degree Taylor polynomial at 0 for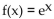 to approximate e0.04. Use Taylor's formula for the remainder to estimate the error in the approximation.
to approximate e0.04. Use Taylor's formula for the remainder to estimate the error in the approximation.
A)
B)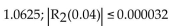
C)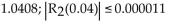
D)
Use the second-degree Taylor polynomial at 0 for
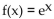 to approximate e0.04. Use Taylor's formula for the remainder to estimate the error in the approximation.
to approximate e0.04. Use Taylor's formula for the remainder to estimate the error in the approximation.A)

B)
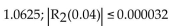
C)
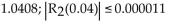
D)


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
48
Use a Taylor series at 0 to approximate the integral with an error of no more than 0.0005.
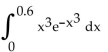
A) 0.0284
B) 0.0286
C) 0.0287
D) 0.0324
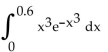
A) 0.0284
B) 0.0286
C) 0.0287
D) 0.0324

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck



