Deck 7: Basic Concepts of Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/61
Play
Full screen (f)
Deck 7: Basic Concepts of Probability
1
Once again using the example about supermarket fliers, we would have evidence that the "don't litter" message on the flier was effective if we found that
A) the probability of finding a flier with the message in the trash can was substantially higher than the probability calculated on the assumption that the two events were independent.
B) the probability of finding a flier with the message in the trash can was substantially lower than the probability calculated on the assumption that the two events were independent.
C) the probability of finding a flier with the message in the trash can was the same as the probability calculated on the assumption that the two events were independent.
D) We can't tell from the information available.
A) the probability of finding a flier with the message in the trash can was substantially higher than the probability calculated on the assumption that the two events were independent.
B) the probability of finding a flier with the message in the trash can was substantially lower than the probability calculated on the assumption that the two events were independent.
C) the probability of finding a flier with the message in the trash can was the same as the probability calculated on the assumption that the two events were independent.
D) We can't tell from the information available.
the probability of finding a flier with the message in the trash can was substantially higher than the probability calculated on the assumption that the two events were independent.
2
To estimate that probability that the next vehicle to leave the parking lot will be a silver pickup, we first need to
A) assume that the color and the type of vehicle are mutually exclusive.
B) assume that the color and the type of vehicle are independent.
C) assume that the color and the type of vehicle are exhaustive.
D) simply multiply the two probabilities.
A) assume that the color and the type of vehicle are mutually exclusive.
B) assume that the color and the type of vehicle are independent.
C) assume that the color and the type of vehicle are exhaustive.
D) simply multiply the two probabilities.
assume that the color and the type of vehicle are independent.
3
A frequentistic approach to probability is likely to be invoked
A) in predicting the weather.
B) in calculating the chances of winning in craps.
C) in estimating the probability that a sharpshooter will score a bull's eye.
D) in blackjack.
A) in predicting the weather.
B) in calculating the chances of winning in craps.
C) in estimating the probability that a sharpshooter will score a bull's eye.
D) in blackjack.
in estimating the probability that a sharpshooter will score a bull's eye.
4
Using the example from the text about the supermarket fliers, when we calculate the probability that a flier will be left either among the canned goods or in the bottom of the shopping cart, we need to invoke
A) the additive rule.
B) the superlative rule.
C) the dependence rule.
D) the multiplicative rule.
A) the additive rule.
B) the superlative rule.
C) the dependence rule.
D) the multiplicative rule.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
5
Last year there were 300 new Ph.D.s in chemistry looking for academic jobs. Of those, 100 were women and 200 were men. Nationwide last year there were 75 new hirings in chemistry departments. How many of those new hires would be expected to be women if there was no gender discrimination?
A) 15
B) 20
C) 25
D) 50
A) 15
B) 20
C) 25
D) 50

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
6
Out of a pool of 40 men and 10 women, all of whom are equally qualified for one position as an instructor in chemistry, the person hired was a male. The probability that this would happen if the department ignored gender as a variable in selection is
A) .40
B) .80
C) .50
D) .63
A) .40
B) .80
C) .50
D) .63

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
7
In the parking lot below me, 40% of the vehicles are silver, and about 25% of the vehicles are pickup trucks. The probability that the next vehicle to leave the parking lot will be a silver pickup is
A) .40
B) .65
C) .10
D) It can't be estimated without knowing that color and type of vehicle are independent.
A) .40
B) .65
C) .10
D) It can't be estimated without knowing that color and type of vehicle are independent.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
8
Two events are mutually exclusive when
A) the occurrence of one event is independent of the occurrence of the other.
B) the occurrence of one event precludes the occurrence of the other.
C) both events are equally likely.
D) the first event precedes the second event.
A) the occurrence of one event is independent of the occurrence of the other.
B) the occurrence of one event precludes the occurrence of the other.
C) both events are equally likely.
D) the first event precedes the second event.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
9
An exhaustive set of events is one which
A) we can never estimate.
B) contains all possible outcomes.
C) contains only independent events.
D) comes from running a very long series of sampling studies.
A) we can never estimate.
B) contains all possible outcomes.
C) contains only independent events.
D) comes from running a very long series of sampling studies.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
10
I am looking down on a parking lot, and can see that about 10% of the cars are red and about 15% of the cars are blue. To estimate the probability that the next car to leave the lot will be red or blue, I would
A) add those two percentages.
B) multiply those two percentages.
C) count the number of green cars.
D) It can't be estimated from the information provided.
A) add those two percentages.
B) multiply those two percentages.
C) count the number of green cars.
D) It can't be estimated from the information provided.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
11
If I am interested in the probability that you will be depressed if you have experienced a great deal of stress in the past month, I am talking about
A) independence.
B) a joint probability.
C) a conditional probability.
D) an additive probability.
A) independence.
B) a joint probability.
C) a conditional probability.
D) an additive probability.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
12
If I am interested in the probability that you will be depressed and that you will have experienced a great deal of stress in the past month, I am talking about
A) independence.
B) a joint probability.
C) a conditional probability.
D) an additive probability.
A) independence.
B) a joint probability.
C) a conditional probability.
D) an additive probability.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
13
When we want to calculate the probability of the joint occurrence of two or more independent events, we invoke
A) the multiplicative rule.
B) the additive rule.
C) the sum of independent probabilities.
D) Bernoulli's rule.
A) the multiplicative rule.
B) the additive rule.
C) the sum of independent probabilities.
D) Bernoulli's rule.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
14
Using an example from the text, when we calculate the probability that a supermarket flier will be left among the canned goods if it contains a notice not to litter, we will be dealing with
A) the additive rule.
B) the superlative rule.
C) the dependence rule.
D) conditional probabilities.
A) the additive rule.
B) the superlative rule.
C) the dependence rule.
D) conditional probabilities.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
15
Which of the following is NOT a way of setting probabilities?
A) the analytic view
B) the frequentistic view
C) the subjective view
D) the correlational view
A) the analytic view
B) the frequentistic view
C) the subjective view
D) the correlational view

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
16
One difference between the additive and the multiplicative rules that helps us remember when to use which is
A) with the additive rule we are talking about the occurrence of one of several outcomes.
B) with the multiplicative rule we are talking about the occurrence of more than one kind of outcome.
C) the two rules are interchangeable.
D) both a and b
A) with the additive rule we are talking about the occurrence of one of several outcomes.
B) with the multiplicative rule we are talking about the occurrence of more than one kind of outcome.
C) the two rules are interchangeable.
D) both a and b

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
17
Where is "subjective probability" most likely to be invoked?
A) in setting the point spread in football
B) in deciding if tomorrow will be a good day
C) in calculating your best strategy in poker
D) in playing Russian roulette
A) in setting the point spread in football
B) in deciding if tomorrow will be a good day
C) in calculating your best strategy in poker
D) in playing Russian roulette

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is NOT an appropriate use of probability?
A) estimating the likelihood that a particular event will occur
B) calculating your chances of winning the lottery
C) placing bets at the track
D) knowing what event will happen next
A) estimating the likelihood that a particular event will occur
B) calculating your chances of winning the lottery
C) placing bets at the track
D) knowing what event will happen next

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
19
Of 50 women treated for breast cancer in the local cancer unit, 35 of them survived for at least 5 years. For a woman who has just been diagnosed with breast cancer, our best guess is that the probability that she will survive for 5 years is
A) 35/50 = .70
B) 15/35= .43
C) 35/100 = .35
D) we don't have enough information.
A) 35/50 = .70
B) 15/35= .43
C) 35/100 = .35
D) we don't have enough information.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
20
Following up on the preceding question, suppose that you found that 27 of the new hires were women. You would probably be justified in concluding that
A) there was discrimination against men.
B) there was discrimination against women.
C) there was no discrimination on the basis of gender.
D) we don't have enough information to even start to answer the question.
A) there was discrimination against men.
B) there was discrimination against women.
C) there was no discrimination on the basis of gender.
D) we don't have enough information to even start to answer the question.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
21
With continuous variables we
A) cannot estimate probabilities because they are undefined.
B) need to speak about the probability of falling within a defined interval.
C) can only speak about probabilities as subjective probabilities.
D) can only calculate probabilities in whole units.
A) cannot estimate probabilities because they are undefined.
B) need to speak about the probability of falling within a defined interval.
C) can only speak about probabilities as subjective probabilities.
D) can only calculate probabilities in whole units.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following is most likely to be a discrete variable?
A) the temperature outside your window
B) the number of courses you will take in college
C) the length of time you can hold your breath
D) the speed with which you can perform a task
A) the temperature outside your window
B) the number of courses you will take in college
C) the length of time you can hold your breath
D) the speed with which you can perform a task

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
23
If a set of events contains all of the possible outcomes, it is said to be
A) mutually exclusive.
B) independent.
C) dependent.
D) exhaustive.
A) mutually exclusive.
B) independent.
C) dependent.
D) exhaustive.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
24
Two events are said to be independent if
A) the occurrence of one precludes the occurrence of the other.
B) the occurrence of both is impossible.
C) both events happen simultaneously.
D) the occurrence of one has no effect on the probability of the occurrence of the other.
A) the occurrence of one precludes the occurrence of the other.
B) the occurrence of both is impossible.
C) both events happen simultaneously.
D) the occurrence of one has no effect on the probability of the occurrence of the other.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
25
Which of the following events are most likely to be independent?
A) your score on your biology midterm and your score on the biology final
B) your mother's attitudes about religion and your father's attitudes about religion
C) the sex of your cousin's first child and the sex of your cousin's second child
D) your philosophy professor's opinion on the meaning of life and your subsequent opinion on the meaning of life
A) your score on your biology midterm and your score on the biology final
B) your mother's attitudes about religion and your father's attitudes about religion
C) the sex of your cousin's first child and the sex of your cousin's second child
D) your philosophy professor's opinion on the meaning of life and your subsequent opinion on the meaning of life

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
26
p(getting a job | knowing the manager) is the notation for the probability of
A) getting a job or knowing the manager.
B) getting a job and knowing the manager.
C) getting a job given that you know the manager.
D) getting a job and not knowing what to give the manager.
A) getting a job or knowing the manager.
B) getting a job and knowing the manager.
C) getting a job given that you know the manager.
D) getting a job and not knowing what to give the manager.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
27
A continuous variable is one that
A) can take on any value between two specified limits.
B) we cannot estimate.
C) can take on a limited number of possible values.
D) can take on any value between - ∞ and + ∞ .
A) can take on any value between two specified limits.
B) we cannot estimate.
C) can take on a limited number of possible values.
D) can take on any value between - ∞ and + ∞ .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
28
We might find that 65% of women report themselves to be politically liberal, while only 52% of men report that they are liberal. The proportions would be described as
A) erroneous.
B) biased.
C) conditional on gender.
D) independent.
A) erroneous.
B) biased.
C) conditional on gender.
D) independent.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
29
Which of the following is NOT a joint probability?
A) the probability that you will have a hyperactive child who is a boy
B) the probability that you will have a hyperactive child who is a girl
C) the probability that your child will be hyperactive given that she is a girl
D) the probability that you live near the ocean and that you enjoy sailing
A) the probability that you will have a hyperactive child who is a boy
B) the probability that you will have a hyperactive child who is a girl
C) the probability that your child will be hyperactive given that she is a girl
D) the probability that you live near the ocean and that you enjoy sailing

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
30
The events most likely to be mutually exclusive are
A) ages.
B) club memberships.
C) your sex and the sex of your siblings.
D) none of the above
A) ages.
B) club memberships.
C) your sex and the sex of your siblings.
D) none of the above

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
31
A discrete variable is one that
A) is kept a secret.
B) we cannot estimate.
C) can take on a limited number of possible values.
D) can take on any value between - ∞ and + ∞ .
A) is kept a secret.
B) we cannot estimate.
C) can take on a limited number of possible values.
D) can take on any value between - ∞ and + ∞ .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
32
Given a normal distribution of intelligence test scores (mean=100, s.d.=15), what is the probability that someone will score between 100 and 115?
A) cannot be determined
B) .15
C) .68
D) .34
A) cannot be determined
B) .15
C) .68
D) .34

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
33
If I am drawing observations out of a hat while sampling with replacement, the probability of drawing a certain outcome
A) remains constant across all draws.
B) changes as I continue drawing objects.
C) decreases as I continue to draw objects.
D) none of the above
A) remains constant across all draws.
B) changes as I continue drawing objects.
C) decreases as I continue to draw objects.
D) none of the above

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
34
When two teams compete against each other, the result for Team A can be win, draw, or lose. These events are
A) independent.
B) exhaustive.
C) joint.
D) conditional.
A) independent.
B) exhaustive.
C) joint.
D) conditional.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
35
The vertical bar "|" is read as _______ when we are talking about probabilities.
A) "absolute"
B) "not"
C) "divide"
D) "given"
A) "absolute"
B) "not"
C) "divide"
D) "given"

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
36
I would like to calculate the probability that you will do well in this course if you are a member of a group of students who study together. The most important word in that last sentence is
A) "if."
B) "calculate."
C) "I."
D) "study."
A) "if."
B) "calculate."
C) "I."
D) "study."

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
37
If Brian has a 50% chance of getting a job, and that job would either be at IBM or AT&T, what is the probability that he will soon be working at IBM?
A) .50 ÷ 2 = .25
B) .50 - p(AT&T)
C) .50 - p(IBM)
D) .50 ÷ p(AT&T)
A) .50 ÷ 2 = .25
B) .50 - p(AT&T)
C) .50 - p(IBM)
D) .50 ÷ p(AT&T)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
38
For which kind of variable is the ordinate of a graph labeled as "density?"
A) a discrete variable
B) a positively skewed variable
C) a continuous variable
D) an independent variable
A) a discrete variable
B) a positively skewed variable
C) a continuous variable
D) an independent variable

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
39
When we sample with replacement we
A) only use subjects who have been selected on two separate occasions.
B) put the outcome back in the pool before sampling again.
C) hold all outcomes out of the pool once they have been drawn.
D) have probabilities that change after each draw.
A) only use subjects who have been selected on two separate occasions.
B) put the outcome back in the pool before sampling again.
C) hold all outcomes out of the pool once they have been drawn.
D) have probabilities that change after each draw.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
40
When we are talking about joint probabilities we are likely to invoke
A) the multiplicative rule.
B) the additive rule.
C) the subjective probability rule.
D) the law of joint probabilities.
A) the multiplicative rule.
B) the additive rule.
C) the subjective probability rule.
D) the law of joint probabilities.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
41
A bag of 100 hard candies included 30 butterscotch, 40 peppermint, 15 strawberry, 10 orange, and 5 banana. The probability that the first candy pulled out of the bag will be butterscotch or strawberry is .45.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
42
Your friend plays the lottery every day. Since he has never won, he is convinced that the odds that he will win next time are even better. From a probability perspective, what is wrong with your friend's logic?

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
43
The probability of rolling a 6 on the first roll with a standard die is independent of the probability of rolling a 6 on the second roll.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
44
A safety agency was interested in whether penalties for talking on a cell phone while driving reduce the probability that individuals will DO SO. They randomly contacted 100 cell phone users. Fifty were from a state that had a law prohibiting this behavior, and 50 were from a state that had no such law. The data follow:
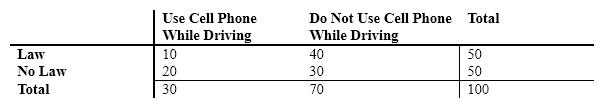
a. Calculate the simple probability that someone uses a cell phone while driving.
b. Calculate the joint probability that someone is in a state without the law and uses their cell phone while driving.
c. Calculate the probability that someone will use their cell phone while driving given they live in state with the law.
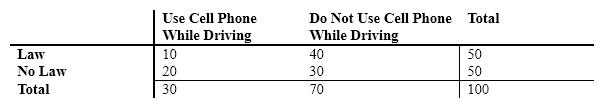
a. Calculate the simple probability that someone uses a cell phone while driving.
b. Calculate the joint probability that someone is in a state without the law and uses their cell phone while driving.
c. Calculate the probability that someone will use their cell phone while driving given they live in state with the law.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
45
A local private school is selling raffle tickets for a new sports car. They plan to sell 10,000 tickets.
a. What is the probability that you will win if you bought 1 ticket?
b. How many tickets are needed to have a .25 probability of winning?
a. What is the probability that you will win if you bought 1 ticket?
b. How many tickets are needed to have a .25 probability of winning?

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
46
Imagine the same bag of marbles, but this time, marbles are NOT returned to the bag after each draw.
a. What is the probability of drawing 3 clear marbles in 3 draws?
b. What is the probability of drawing a clear marble, then a green, and then a clear?
c. What is the probability of not selecting any clear marbles in three draws?
a. What is the probability of drawing 3 clear marbles in 3 draws?
b. What is the probability of drawing a clear marble, then a green, and then a clear?
c. What is the probability of not selecting any clear marbles in three draws?

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
47
If the probability is .90 that a student taking this class is a Psychology major, and the probability that a student in this class has red hair is .05, then the joint probability of being a Psychology major and a red head in this class is .95.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
48
Explain why it is important to know if someone is sampling with or without replacement when calculating the probability of multiple events.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
49
A kindergarten teacher assigns chores to her students on a weekly basis. One student works on each task, and each student is assigned only one task a week. During the first week of school, there were 20 students and 7 tasks. Also, 4 of the students had brown hair.
a. What is the probability that a student would not be assigned a chore?
b. What is the probability that a student had brown hair?
c. What is the probability that a student had brown hair or had a chore?
d. What is the probability that a student had brown hair and a chore?
a. What is the probability that a student would not be assigned a chore?
b. What is the probability that a student had brown hair?
c. What is the probability that a student had brown hair or had a chore?
d. What is the probability that a student had brown hair and a chore?

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
50
When observing a continuous variable, you can calculate the probability that an event falls in a certain interval; and when observing a discrete variable, you can calculate the probability of a specific outcome.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
51
A bag of 100 marbles contains 30 blue marbles, 25 green marbles, 25 mixed green/blue marbles, and 20 clear marbles. Marbles are returned to the bag after every draw.
a. What is the probability of selecting a blue marble?
b. What is the probability of selecting a blue or green marble?
c. What is the probability of selecting a marble that is not clear?
d. What is the probability of selecting a blue marble on the first draw and then a clear marble on the second draw?
a. What is the probability of selecting a blue marble?
b. What is the probability of selecting a blue or green marble?
c. What is the probability of selecting a marble that is not clear?
d. What is the probability of selecting a blue marble on the first draw and then a clear marble on the second draw?

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
52
Two events are mutually exclusive if
A) they cannot both happen at the same time.
B) they cover all possibilities.
C) one of them must happen.
D) none of the above
A) they cannot both happen at the same time.
B) they cover all possibilities.
C) one of them must happen.
D) none of the above

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
53
If the average score on the Graduate Record Exam was 500 and the standard deviation was 100, what is the probability that a random student would score between 400 and 600?

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
54
I have a hunch that tomorrow is going to be a bad day. This is an example of the subjective probability.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
55
Predicting the political party of the next president based on previous election patterns is an example of the relative frequency view of probability.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
56
Dealing 5 cards from a standard deck is an example of sampling with replacement.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
57
Identify each of the following examples as the analytic, relative frequency, or subjective view of probability based on the example of a brother and sister playing scrabble:
a. If the brother and sister are equally matched, there is a .50 probability that each will win the game.
b. If the sister won 3 of the last 4 games, the probability that she will win this one is .75.
c. The brother believes there is an 80% chance that he will beat his sister this time.
a. If the brother and sister are equally matched, there is a .50 probability that each will win the game.
b. If the sister won 3 of the last 4 games, the probability that she will win this one is .75.
c. The brother believes there is an 80% chance that he will beat his sister this time.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
58
The probability that a student is a Psychology major given that she is female is an example of joint probability.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
59
The probability of getting heads twice when flipping a coin 2 times is .50.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
60
The probability that an event will occur ranges from -1 to 1.

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
61
A professor rated how frequently students actively participated in class and then calculated the probability of getting various grades broken down by participation. The data follow:

a. What is the simple probability of getting an A?
b. What is the probability of getting an A given the student participated frequently?
c. What is the simple probability of failing?
d. What is the probability of failing given the student participated rarely/never?

a. What is the simple probability of getting an A?
b. What is the probability of getting an A given the student participated frequently?
c. What is the simple probability of failing?
d. What is the probability of failing given the student participated rarely/never?

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck



