Deck 10: Conics
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/89
Play
Full screen (f)
Deck 10: Conics
1
Write the standard form of the equation of the parabola with focus (4,5) and its vertex at (9,5).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Write the standard form of the equation of the circle with the center at (0,0) that has a radius of 6.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Write the standard form of the equation of the circle with the center at (4,2) that has radius 4.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Graph the equation .
A)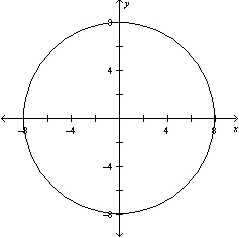
B)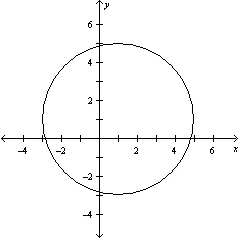
C)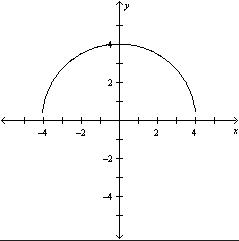
D)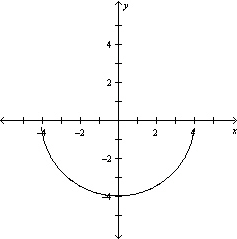
E)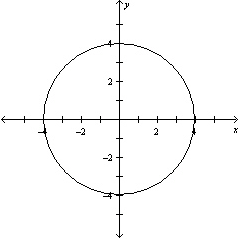
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
5
Graph the equation .
A)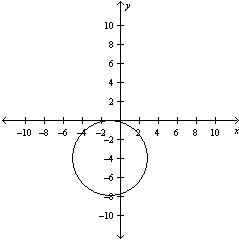
B)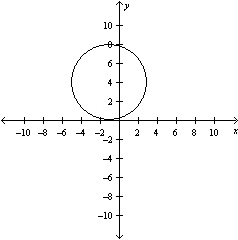
C)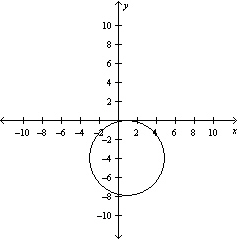
D)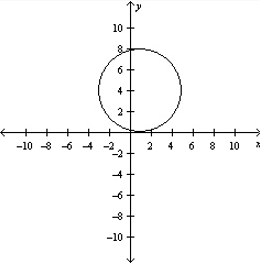
E)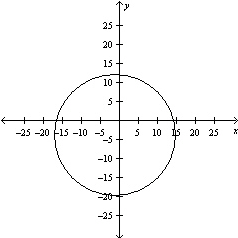
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
6
Graph the equation .
A)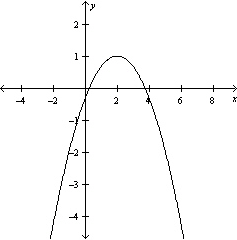
B)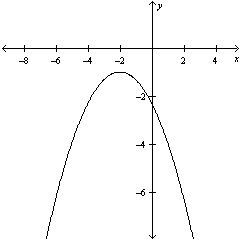
C)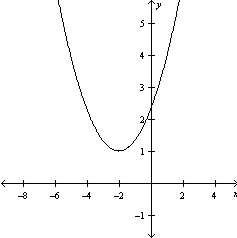
D)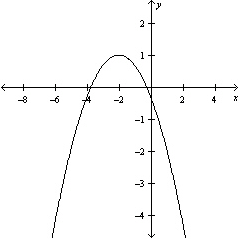
E)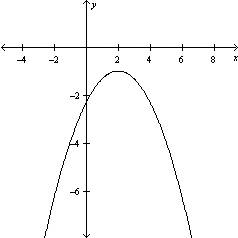
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
7
Write the standard form of the equation of the circle with the center at (0,0) that passes through the point (6,2) .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
8
Identify the center and radius of the circle .
A)center: (12,6) radius: 216
B)center: (-6,-3) radius: 9
C)center: (6,3) radius: 36
D)center: (6,3) radius: 9
E)center: (12,6) radius: 36
A)center: (12,6) radius: 216
B)center: (-6,-3) radius: 9
C)center: (6,3) radius: 36
D)center: (6,3) radius: 9
E)center: (12,6) radius: 36

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
9
Graph the equation .
A)
B)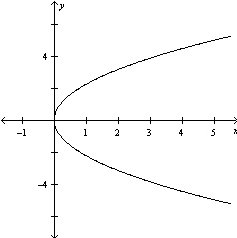
C)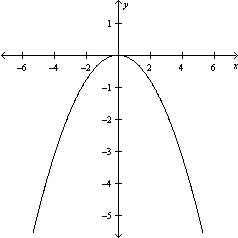
D)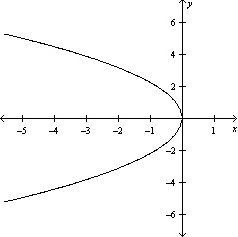
E)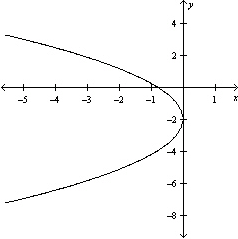
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
10
Identify the center and radius of the circle .
A)center: (1,1) radius: 25
B)center: (5,5) radius: 5
C)center: (0,0) radius: 5
D)center: (5,5) radius: 1
E)center: (0,0) radius: 25
A)center: (1,1) radius: 25
B)center: (5,5) radius: 5
C)center: (0,0) radius: 5
D)center: (5,5) radius: 1
E)center: (0,0) radius: 25

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
11
Identify the center and radius of the circle .
A)center: (-7,-2) radius: 9
B)center: (2,7) radius: 9
C)center: (2,7) radius: 81
D)center: (-2,-7) radius: 9
E)center: (7,2) radius: 81
A)center: (-7,-2) radius: 9
B)center: (2,7) radius: 9
C)center: (2,7) radius: 81
D)center: (-2,-7) radius: 9
E)center: (7,2) radius: 81

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
12
Graph the equation .
A)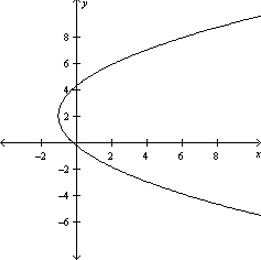
B)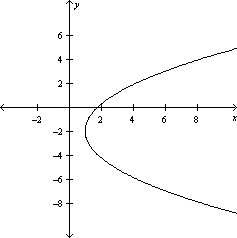
C)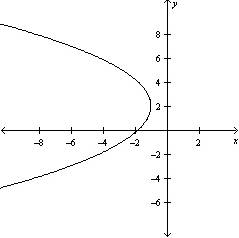
D)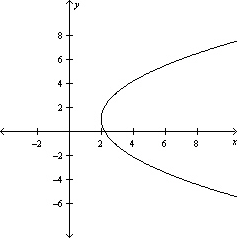
E)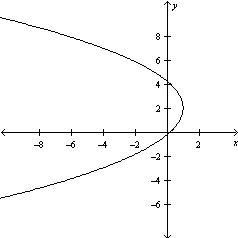
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
13
Write the standard form of the equation of the circle with the center at (0,2) that passes through the point (7,3) .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
14
Graph the equation .
A)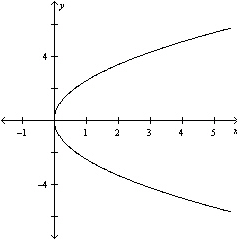
B)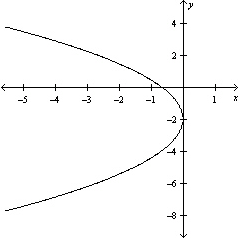
C)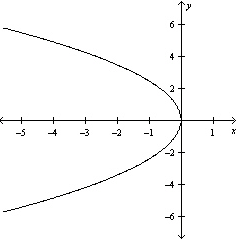
D)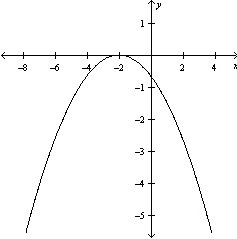
E)
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
15
Identify the center and radius of the circle .
A)center: (3,3) radius: 4
B)center: (0,0) radius:
C)center: (0,0) radius:
D)center: (0,4) radius:
E)center: (0,4) radius:
A)center: (3,3) radius: 4
B)center: (0,0) radius:
C)center: (0,0) radius:
D)center: (0,4) radius:
E)center: (0,4) radius:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
16
Identify the center and radius of the circle .
A)center: radius: 535
B)center: radius: 45
C)center: radius: 10
D)center: radius: 45
E)center: radius: 10
A)center: radius: 535
B)center: radius: 45
C)center: radius: 10
D)center: radius: 45
E)center: radius: 10

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
17
Identify the center and radius of the circle .
A)center: (0,0) radius:
B)center: (1,1) radius: 4
C)center: (1,1) radius: 2
D)center: (2,2) radius: 1
E)center: (0,0) radius:
A)center: (0,0) radius:
B)center: (1,1) radius: 4
C)center: (1,1) radius: 2
D)center: (2,2) radius: 1
E)center: (0,0) radius:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
18
Write the standard form of the equation of the parabola with focus (0,-2) and its vertex at the origin.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
19
Write the standard form of the equation of the parabola with focus (-9,0) and its vertex at the origin.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
20
Write the standard form of the equation of the parabola with focus (-5,5) and its vertex at (-5,8) .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
21
Write the standard form of the equation of the ellipse centered at the origin. Vertices: Co-vertices:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
22
Write the standard form of the equation of the ellipse. 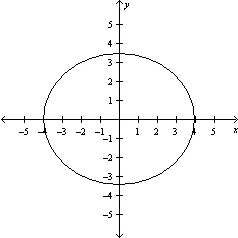
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
23
Write the standard form of the equation of the ellipse. 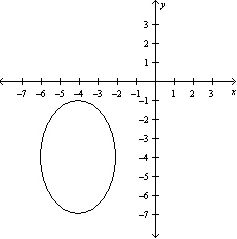
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
24
Write the standard form of the equation of the ellipse. 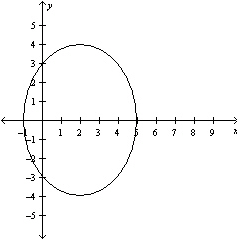
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
25
Identify the vertices and co-vertices of the ellipse .
A)vertices: co-vertices:
B)vertices: co-vertices:
C)vertices: co-vertices:
D)vertices: co-vertices:
E)vertices: co-vertices:
A)vertices: co-vertices:
B)vertices: co-vertices:
C)vertices: co-vertices:
D)vertices: co-vertices:
E)vertices: co-vertices:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
26
Identify the vertex and focus of the parabola .
A)vertex: focus:
B)vertex: focus:
C)vertex: focus:
D)vertex: focus:
E)vertex: focus:
A)vertex: focus:
B)vertex: focus:
C)vertex: focus:
D)vertex: focus:
E)vertex: focus:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
27
Identify the vertex and focus of the parabola .
A)vertex: (0,0) focus:
B)vertex: (0,0) focus:
C)vertex: (0,0) focus: (-7,0)
D)vertex: (0,0) focus:
E)vertex: (0,0) focus:
A)vertex: (0,0) focus:
B)vertex: (0,0) focus:
C)vertex: (0,0) focus: (-7,0)
D)vertex: (0,0) focus:
E)vertex: (0,0) focus:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
28
Graph the function .
A)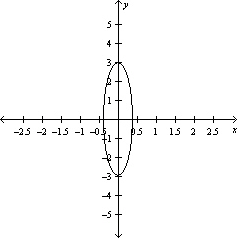
B)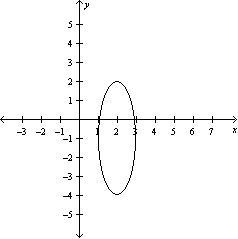
C)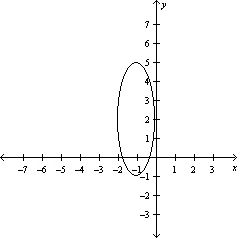
D)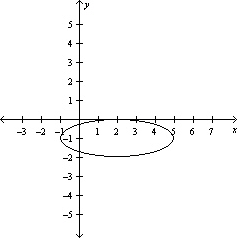
E)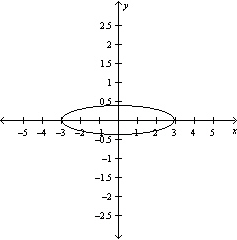
A)
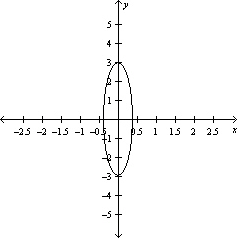
B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
29
Graph the function .
A)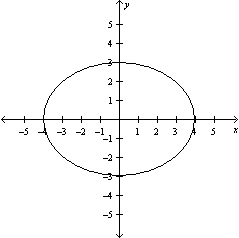
B)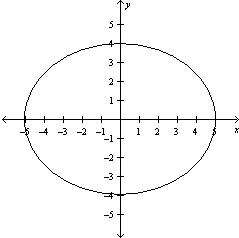
C)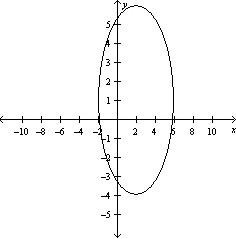
D)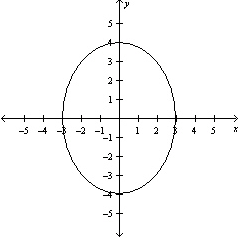
E)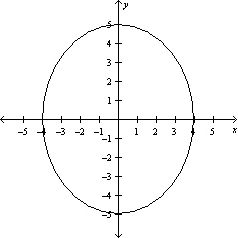
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
30
Identify the vertices and center of the ellipse .
A)vertices: center: (5,2)
B)vertices: center: (5,2)
C)vertices: center: (-5,-2)
D)vertices: center: (-5,-2)
E)vertices: center: (5,2)
A)vertices: center: (5,2)
B)vertices: center: (5,2)
C)vertices: center: (-5,-2)
D)vertices: center: (-5,-2)
E)vertices: center: (5,2)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
31
Write the standard form of the equation of the ellipse. 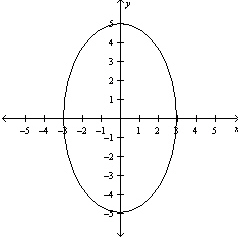
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
32
Identify the vertex and focus of the parabola .
A)vertex: focus:
B)vertex: focus:
C)vertex: focus:
D)vertex: focus:
E)vertex: focus:
A)vertex: focus:
B)vertex: focus:
C)vertex: focus:
D)vertex: focus:
E)vertex: focus:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
33
A semicircular arch for a tunnel under a river has a diameter of 80 feet (see figure). Determine the height of the arch 4 feet from the edge of the tunnel. 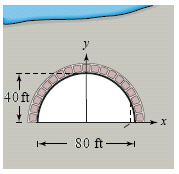
A)36 feet
B) feet
C) feet
D) feet
E) feet

A)36 feet
B) feet
C) feet
D) feet
E) feet

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
34
Identify the vertex and focus of the parabola .
A)vertex: (0,0) focus:
B)vertex: (0,0) focus:
C)vertex: (0,0) focus:
D)vertex: (0,0) focus:
E)vertex: (0,0) focus:
A)vertex: (0,0) focus:
B)vertex: (0,0) focus:
C)vertex: (0,0) focus:
D)vertex: (0,0) focus:
E)vertex: (0,0) focus:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
35
Write the standard form of the equation of the ellipse centered at the origin, having a horizontal major axis of 6 units and a minor axis of 4 units.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
36
Identify the vertices and co-vertices of the ellipse .
A)vertices: co-vertices:
B)vertices: co-vertices:
C)vertices: co-vertices:
D)vertices: co-vertices:
E)vertices: co-vertices:
A)vertices: co-vertices:
B)vertices: co-vertices:
C)vertices: co-vertices:
D)vertices: co-vertices:
E)vertices: co-vertices:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
37
Identify the vertices and co-vertices of the ellipse .
A)vertices: co-vertices:
B)vertices: co-vertices:
C)vertices: co-vertices:
D)vertices: co-vertices:
E)vertices: co-vertices:
A)vertices: co-vertices:
B)vertices: co-vertices:
C)vertices: co-vertices:
D)vertices: co-vertices:
E)vertices: co-vertices:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
38
Write the standard form of the equation of the ellipse centered at the origin, having a vertical 20 units and a minor axis of 10 units.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
39
Graph the function .
A)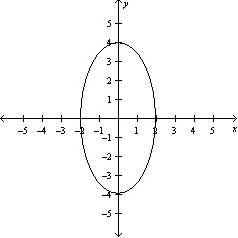
B)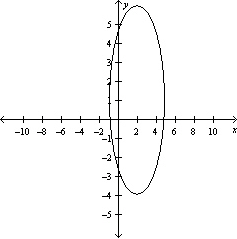
C)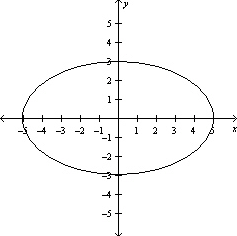
D)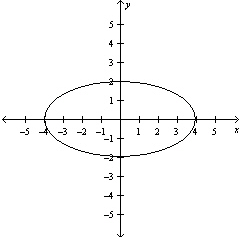
E)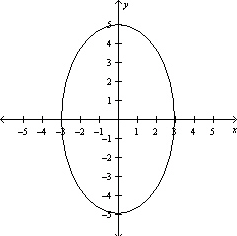
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
40
Graph the function .
A)
B)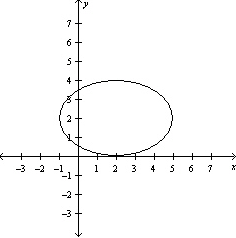
C)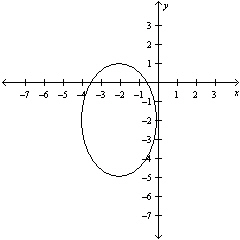
D)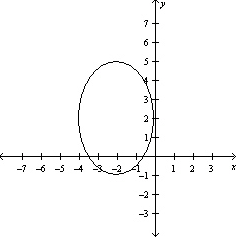
E)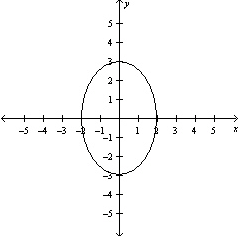
A)

B)
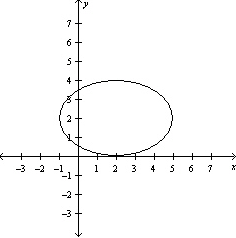
C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
41
Write the standard form of the equation of the hyperbola centered at the origin. Vertices: Asymptotes:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
42
Identify the vertices and asymptotes of the hyperbola.
A)vertices: asymptotes:
B)vertices: asymptotes:
C)vertices: asymptotes:
D)vertices: asymptotes:
E)vertices: asymptotes:
A)vertices: asymptotes:
B)vertices: asymptotes:
C)vertices: asymptotes:
D)vertices: asymptotes:
E)vertices: asymptotes:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
43
Identify the vertices and asymptotes of the hyperbola.
A)vertices: asymptotes:
B)vertices: asymptotes:
C)vertices: asymptotes:
D)vertices: asymptotes:
E)vertices: asymptotes:
A)vertices: asymptotes:
B)vertices: asymptotes:
C)vertices: asymptotes:
D)vertices: asymptotes:
E)vertices: asymptotes:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
44
Graph the hyperbola.
A)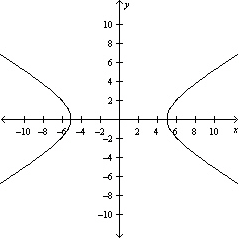
B)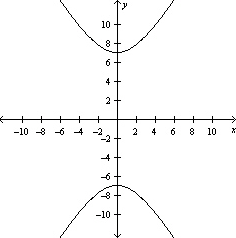
C)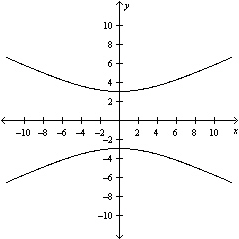
D)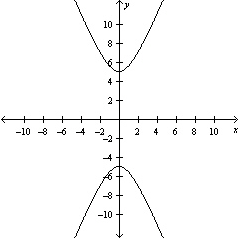
E)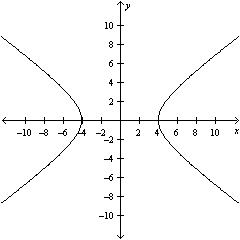
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
45
Write the standard form of the equation of the hyperbola centered at the origin. Vertices: Asymptotes:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
46
Identify the vertices and asymptotes of the hyperbola.
A)vertices: asymptotes:
B)vertices: asymptotes:
C)vertices: asymptotes:
D)vertices: asymptotes:
E)vertices: asymptotes:
A)vertices: asymptotes:
B)vertices: asymptotes:
C)vertices: asymptotes:
D)vertices: asymptotes:
E)vertices: asymptotes:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
47
Graph the hyperbola.
A)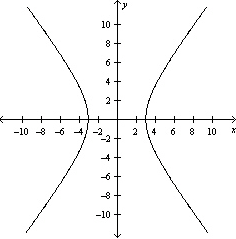
B)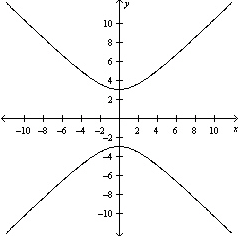
C)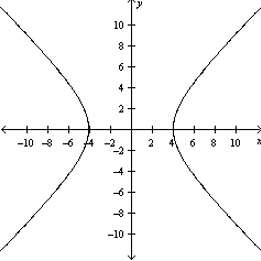
D)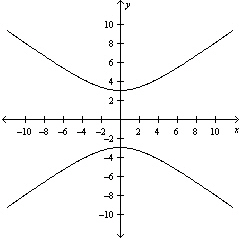
E)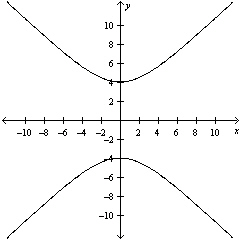
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
48
Identify the vertices and asymptotes of the hyperbola.
A)vertices: asymptotes:
B)vertices: asymptotes:
C)vertices: asymptotes:
D)vertices: asymptotes:
E)vertices: asymptotes:
A)vertices: asymptotes:
B)vertices: asymptotes:
C)vertices: asymptotes:
D)vertices: asymptotes:
E)vertices: asymptotes:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
49
Identify the vertices and center of the ellipse.
A)vertices: center: (-1,4)
B)vertices: center: (-1,4)
C)vertices: center: (-1,4)
D)vertices: center: (1,-4)
E)vertices: center: (1,-4)
A)vertices: center: (-1,4)
B)vertices: center: (-1,4)
C)vertices: center: (-1,4)
D)vertices: center: (1,-4)
E)vertices: center: (1,-4)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
50
Graph the hyperbola.
A)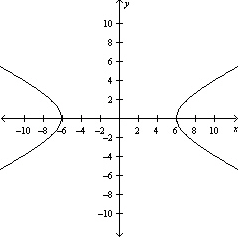
B)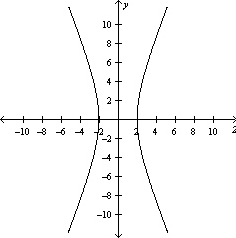
C)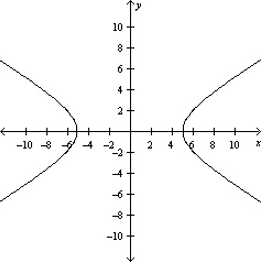
D)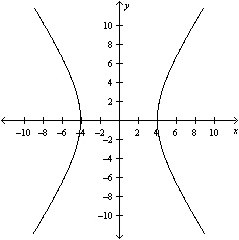
E)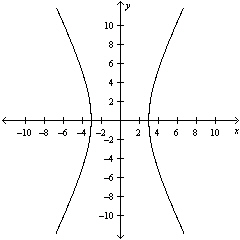
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
51
A semielliptical arch for a tunnel under a river has a width of 80 feet and a height of 30 feet (see figure). Determine the height of the arch 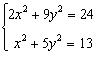 feet from the edge of the tunnel. Round your answer to one decimal place.
feet from the edge of the tunnel. Round your answer to one decimal place. 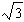
A)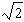 feet
feet
B)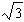 feet
feet
C)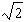 feet
feet
D)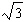 feet
feet
E)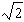 feet
feet
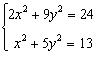 feet from the edge of the tunnel. Round your answer to one decimal place.
feet from the edge of the tunnel. Round your answer to one decimal place. 
A)
 feet
feetB)
 feet
feetC)
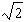 feet
feetD)
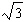 feet
feetE)
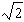 feet
feet
Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
52
Write the standard form of the equation of the hyperbola centered at the origin. Vertices: Asymptotes:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
53
Graph the hyperbola.
A)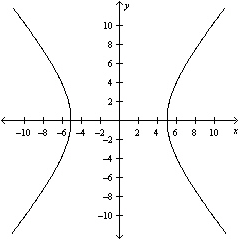
B)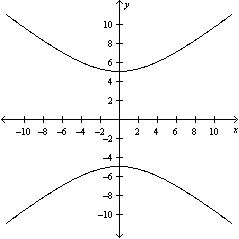
C)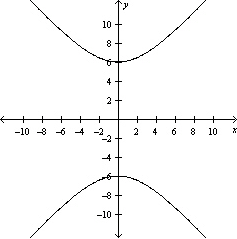
D)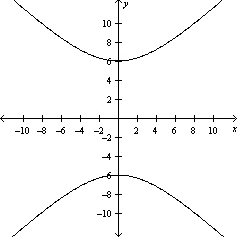
E)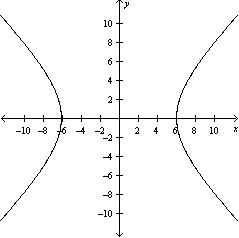
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
54
Identify the vertices and center of the ellipse.
A)vertices: center: (2,-6)
B)vertices: center: (2,-6)
C)vertices: center: (-2,6)
D)vertices: center: (2,-6)
E)vertices: center: (-2,6)
A)vertices: center: (2,-6)
B)vertices: center: (2,-6)
C)vertices: center: (-2,6)
D)vertices: center: (2,-6)
E)vertices: center: (-2,6)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
55
Sketch the graph of the equation.
A)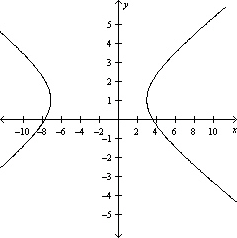
B)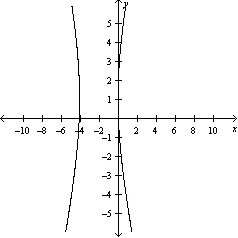
C)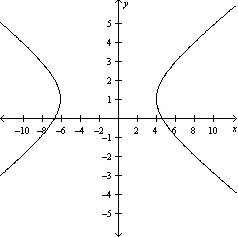
D)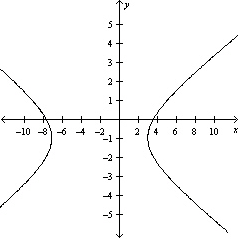
E)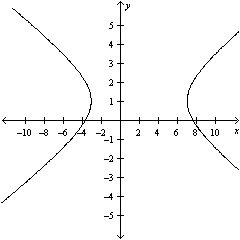
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
56
Sketch the graph of the equation.
A)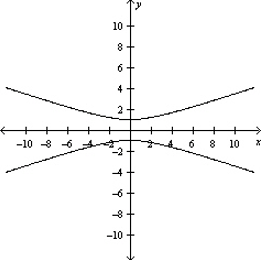
B)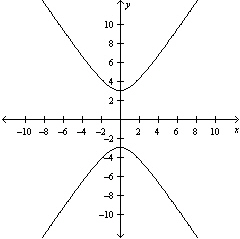
C)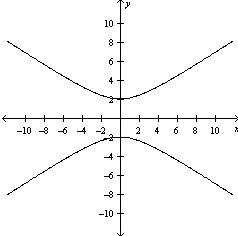
D)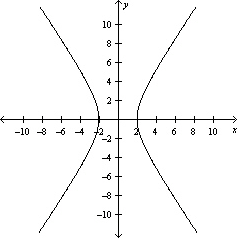
E)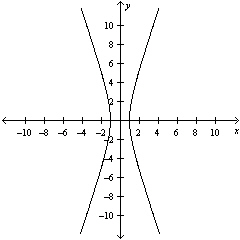
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
57
Identify the center and vertices of the hyperbola.
A)center: vertices:
B)center: vertices:
C)center: vertices:
D)center: vertices:
E)center: vertices:
A)center: vertices:
B)center: vertices:
C)center: vertices:
D)center: vertices:
E)center: vertices:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
58
Sketch the graph of the equation.
A)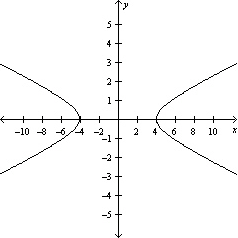
B)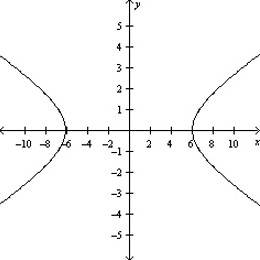
C)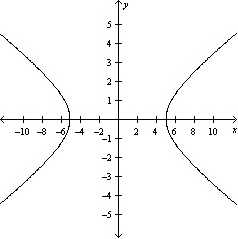
D)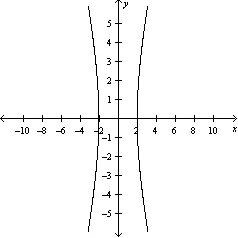
E)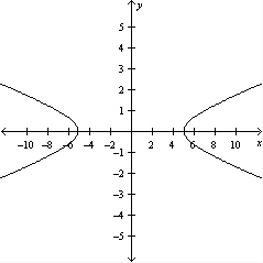
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
59
Identify the vertices and center of the ellipse.
A)vertices: center: (-4,-1)
B)vertices: center: (4,1)
C)vertices: center:
D)vertices: center:
E)vertices: center:
A)vertices: center: (-4,-1)
B)vertices: center: (4,1)
C)vertices: center:
D)vertices: center:
E)vertices: center:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
60
Identify the vertices and center of the ellipse.
A)vertices: center: (-2,3)
B)vertices: center: (2,3)
C)vertices: center: (2,-3)
D)vertices: center: (-2,-3)
E)vertices: center: (-2,3)
A)vertices: center: (-2,3)
B)vertices: center: (2,3)
C)vertices: center: (2,-3)
D)vertices: center: (-2,-3)
E)vertices: center: (-2,3)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the system by the method of substitution.
A)
B)
C)
D)
E)no solution exist
A)
B)
C)
D)
E)no solution exist

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
62
Write the standard form of the equation of the hyperbola. 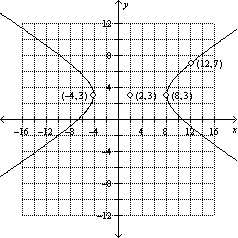
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
63
Sketch the graph of the equation.
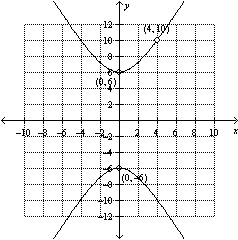
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
64
Use a graphing calculator to graph the equations and find the solutions of the system.
A)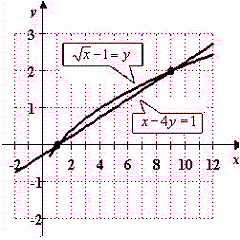
B)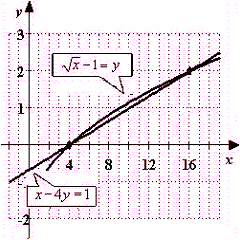
C)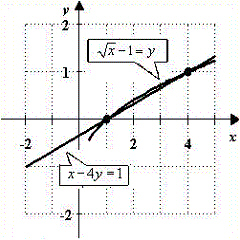
D)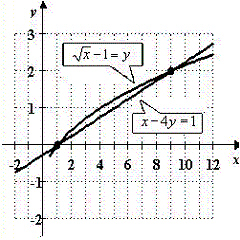
E)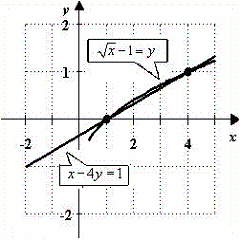
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
65
Graph the equations to determine whether the system has any solutions. Find any solutions that exist.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
66
Graph the equations to determine whether the system has any solutions. Find any solutions that exist.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
67
Sketch the graph of the equation.
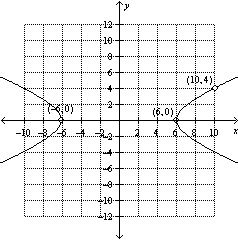
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the system by the method of substitution.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the system by the method of substitution.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
70
Identify the center and vertices of the hyperbola.
A)center: (2,-6) vertices:
B)center: (2,-6) vertices:
C)center: (-2,6) vertices:
D)center: (2,-6) vertices:
E)center: vertices:
A)center: (2,-6) vertices:
B)center: (2,-6) vertices:
C)center: (-2,6) vertices:
D)center: (2,-6) vertices:
E)center: vertices:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
71
Graph the equations to determine whether the system has any solutions. Find any solutions that exist.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
72
Identify the center and vertices of the hyperbola.
A)center: (0,5) vertices:
B)center: (0,-5) vertices:
C)center: vertices:
D)center: vertices:
E)center: vertices:
A)center: (0,5) vertices:
B)center: (0,-5) vertices:
C)center: vertices:
D)center: vertices:
E)center: vertices:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
73
Graph the equations to determine whether the system has any solutions. Find any solutions that exist.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
74
Graph the equations to determine whether the system has any solutions. Find any solutions that exist.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
75
Write the standard form of the equation of the hyperbola. 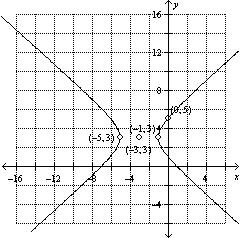
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the system by the method of substitution.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the system by the method of substitution.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the system by the method of substitution.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
79
Identify the center and vertices of the hyperbola.
A)center: (5,-3) vertices:
B)center: (-5,3) vertices:
C)center: vertices:
D)center: vertices:
E)center: vertices:
A)center: (5,-3) vertices:
B)center: (-5,3) vertices:
C)center: vertices:
D)center: vertices:
E)center: vertices:

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the system by the method of substitution.
A)
B)
C)
D)
E)no solution exists
A)
B)
C)
D)
E)no solution exists

Unlock Deck
Unlock for access to all 89 flashcards in this deck.
Unlock Deck
k this deck



