Deck 19: Logistic Regression
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/15
Play
Full screen (f)
Deck 19: Logistic Regression
1
Complete the missing information for this table (Y is a dichotomous variable).
P(Y = 0) = 1 -P(Y = 1). Odds(Y = 1) = P(Y = 1)/P(Y = 0)
The complete table can be obtained as follows.
The complete table can be obtained as follows.
2
You are given the following data, where X1 (high school cumulative GPA) and X2 (having repeated grade; 0 = never repeated any grade and 1 = have repeated at least one grade; use 0 as the reference category) are used to predict Y (dropping out of high school, "1," vs. graduating high school, "0").
( = .05)
Determine the following values based on simultaneous entry of the independent variables: -2LL, constant, b1, b2, se(b1), se(b2), odds ratios, Wald1, Wald2.
( = .05)
Determine the following values based on simultaneous entry of the independent variables: -2LL, constant, b1, b2, se(b1), se(b2), odds ratios, Wald1, Wald2.
-2LL = 5.048;
b1(GPA) = ?6.617, b2(Repeat) = 3.204, bconstant = 14.123;
se(b1(GPA)) = 4.308, se(b2(Repeat)) = 3.387;
odds ratio1(GPA) = .001, odds ratio2(Repeat) = 24.631;
Wald1(GPA) = 2.359, Wald2(Athletics) = .895.
Procedure:
Create a data set with three variables: GPA (X1), Repeat (X2), and Dropout (Y). The data set should have 10 cases.
Step 1: Go to Analyze Regression Binary Logistic.
Step 2: Select Dropout to the Dependent box. Select GPA and Repeat to the Covariate(s) list.
Step 3: Click Categorical. Move Repeat into the Categorical Covariates box. Select Reference Category: First. Click Change. Click Continue.
Step 4: Click Save. Check Probabilities and Group membership under Predicted Values. Check Standardized under Residuals. Check Cook's, Leverage values, and DfBeta(s) under Influences. Click Continue.
Step 5: Click Options. Check Classification plots, Hosmer-Lemeshow goodness-of -fit, Casewise listing of residuals, and CI for exp(B) under Statistics and Plots. Click Continue. Click OK.
Selected SPSS output:
b1(GPA) = ?6.617, b2(Repeat) = 3.204, bconstant = 14.123;
se(b1(GPA)) = 4.308, se(b2(Repeat)) = 3.387;
odds ratio1(GPA) = .001, odds ratio2(Repeat) = 24.631;
Wald1(GPA) = 2.359, Wald2(Athletics) = .895.
Procedure:
Create a data set with three variables: GPA (X1), Repeat (X2), and Dropout (Y). The data set should have 10 cases.
Step 1: Go to Analyze Regression Binary Logistic.
Step 2: Select Dropout to the Dependent box. Select GPA and Repeat to the Covariate(s) list.
Step 3: Click Categorical. Move Repeat into the Categorical Covariates box. Select Reference Category: First. Click Change. Click Continue.
Step 4: Click Save. Check Probabilities and Group membership under Predicted Values. Check Standardized under Residuals. Check Cook's, Leverage values, and DfBeta(s) under Influences. Click Continue.
Step 5: Click Options. Check Classification plots, Hosmer-Lemeshow goodness-of -fit, Casewise listing of residuals, and CI for exp(B) under Statistics and Plots. Click Continue. Click OK.
Selected SPSS output:
3
Complete the missing information for Table 1, using 0.50 as the cut value. Then complete the classification table (Table 2). Compute sensitivity, specificity, false positive rate, and false negative rate.
Assuming 0.5 is the cut value, cases with predicted probabilities at .5 or above are predicted as 1 and predicted probabilities below .5 are predicted as 0. There are four cases with observed value 1 and predicted value 1. There are three cases with observed value 0 and predicted value 0. There is one case with observed value 0 yet predicted value 1 (false positive).
There are two cases with observed value 1 yet predicted value 0 (false negative).
Sensitivity = 4/(2+4) = 0.67 = 67%
Specificity = 3/(3+1) = 0.75 = 75%
False positive rate = 1/(3+1) = 0.25 -25%
False negative rate = 2/(2+4) = 0.33 = 33%
There are two cases with observed value 1 yet predicted value 0 (false negative).
Sensitivity = 4/(2+4) = 0.67 = 67%
Specificity = 3/(3+1) = 0.75 = 75%
False positive rate = 1/(3+1) = 0.25 -25%
False negative rate = 2/(2+4) = 0.33 = 33%
4
You are given the following data, where X1 (sex; male = 0, female =1; use 0 as the reference category) and X2 (having at least one immediate family member who smokes; yes = 1, no = 0; use 0 as the reference category) are used to predict Y (being a smoker = 1 vs. being a nonsmoker = 0).
( = .05)
Determine the following values based on simultaneous entry of independent variables: -2LL, constant, b1, b2, se(b1), se(b2), odds ratios, Wald1, Wald2.
( = .05)
Determine the following values based on simultaneous entry of independent variables: -2LL, constant, b1, b2, se(b1), se(b2), odds ratios, Wald1, Wald2.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
5
Professor Pruefung wanted to examine if performance in quizzes can predict whether a student will pass or fail the final exam. The independent variables are scores in two pop quizzes (Quiz1, Quiz2), and the dependent variable is a dichotomous variable (pass = 1 vs. fail = 0). Below is part of the output of the analysis.
a. Professor Pruefung assumed that the better a student performed in the quizzes (a higher score indicates better performance), the higher the odds that he/she will pass the final exam. If that is the case, what are the expected signs for b1 and b2? Do the results confirm the expectation?
b. Based on the tables, is there any indication of assumptions violation? If so, which assumption(s) has (have) been violated?
c. What are the possible consequences of the assumption violation?
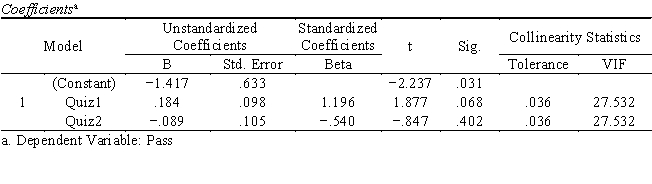
a. Professor Pruefung assumed that the better a student performed in the quizzes (a higher score indicates better performance), the higher the odds that he/she will pass the final exam. If that is the case, what are the expected signs for b1 and b2? Do the results confirm the expectation?
b. Based on the tables, is there any indication of assumptions violation? If so, which assumption(s) has (have) been violated?
c. What are the possible consequences of the assumption violation?


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
6
Which one of the following can be used as an appropriate dependent variable for binary logistic regression?
A) Dichotomous variable
B) Multinomial variable
C) Continuous variable
D) None of the above
E) All of the above
A) Dichotomous variable
B) Multinomial variable
C) Continuous variable
D) None of the above
E) All of the above

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
7
A study was conducted to investigate variables associated with dropping out of high school.
The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1 = dropped out of high school; 0 = did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-What is being predicted in this model?
A) The mean difference in cumulative GPA between students who dropped out of high school and those who finished high school.
B) The percentage of students who will drop out before graduating high school.
C) The odds that a student will drop out of high school.
D) The odds that a student had been retained in at least one grade if he dropped out of high school.
The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1 = dropped out of high school; 0 = did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-What is being predicted in this model?
A) The mean difference in cumulative GPA between students who dropped out of high school and those who finished high school.
B) The percentage of students who will drop out before graduating high school.
C) The odds that a student will drop out of high school.
D) The odds that a student had been retained in at least one grade if he dropped out of high school.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
8
A study was conducted to investigate variables associated with dropping out of high school.
The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1 = dropped out of high school; 0 = did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-Based on logistic regression, if a student has been retained in at least one grade, the chance that he/she will drop out of high school
A) increases.
B) decreases.
C) stays the same.
D) is uncertain.
The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1 = dropped out of high school; 0 = did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-Based on logistic regression, if a student has been retained in at least one grade, the chance that he/she will drop out of high school
A) increases.
B) decreases.
C) stays the same.
D) is uncertain.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
9
A study was conducted to investigate variables associated with dropping out of high school.
The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1 = dropped out of high school; 0 = did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-If Mindy has a high school GPA of 3, and has never repeated a grade, which of the following predictions can be derived from the model?
A) Mindy has more than 50% probability of dropping out of high school.
B) Mindy has less than 50% probability of dropping out of high school.
C) Mindy has exactly 50% probability of dropping out of high school.
D) Mindy will drop out of high school.
E) Mindy will not drop out of high school.
The following logistic regression model was obtained:
Logit(Yi) = 3.5 - 1.3X1 + 2.3X2.
Y: 1 = dropped out of high school; 0 = did not drop out of high school;
X1: cumulative high school GPA obtained;
X2: 1 = retained in at least one grade; 0 = never retained in any grade.
-If Mindy has a high school GPA of 3, and has never repeated a grade, which of the following predictions can be derived from the model?
A) Mindy has more than 50% probability of dropping out of high school.
B) Mindy has less than 50% probability of dropping out of high school.
C) Mindy has exactly 50% probability of dropping out of high school.
D) Mindy will drop out of high school.
E) Mindy will not drop out of high school.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
10
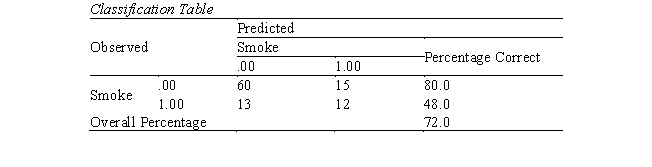
-Aaron is studying smoking behavior and has coded "smoker" as "1" and "nonsmoker" as "0." The predictor is the number of family members who smoke. Which of the following is a correct interpretation of an odds ratio of +2?
A) For every additional family member who smokes, the odds of being a smoker increase by 100%.
B) For every additional family member who smokes, the odds of being a smoker decrease by 100%.
C) For every one-unit increase in being a smoker, the odds of having a family member who smoke increase by 100%.
D) For every one-unit increase in being a smoker, the odds of having a family member who smoke decrease by 100%.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
11

-What is the false positive rate?
A) 20%
B) 28%
C) 48%
D) 52%

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
12

-What is the false negative rate?
A) 20%
B) 28%
C) 48%
D) 52%

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
13
If a person is predicted to be a smoker, we would expect that
A) the person has a good chance of actually being a smoker, because the model has an adequate overall predictive accuracy.
B) the person has a good chance of actually being a smoker, because the model has high specificity.
C) the person may or may not be a smoker, because the model has low sensitivity.
D) the person may or may not be a smoker, because the false positive rate is high.
A) the person has a good chance of actually being a smoker, because the model has an adequate overall predictive accuracy.
B) the person has a good chance of actually being a smoker, because the model has high specificity.
C) the person may or may not be a smoker, because the model has low sensitivity.
D) the person may or may not be a smoker, because the false positive rate is high.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
14
The odds ratio is computed by which of the following?
A) bᵉ
B) b⁻¹/²
C) eᵇᵏ
D) eʳᵇ
A) bᵉ
B) b⁻¹/²
C) eᵇᵏ
D) eʳᵇ

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
15
Which one of the following can occur when the number of variables equals, or nearly equals, the number of cases in the data?
A) Extremely small regression coefficients and standard errors.
B) The dependent variable is perfectly predicted.
C) The maximum likelihood estimator reduces to zero.
D) The outcome is constant for one or more categories of a nominal independent variable.
A) Extremely small regression coefficients and standard errors.
B) The dependent variable is perfectly predicted.
C) The maximum likelihood estimator reduces to zero.
D) The outcome is constant for one or more categories of a nominal independent variable.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck



