Deck 6: Eis Other Physical Phenomena
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/34
Play
Full screen (f)
Deck 6: Eis Other Physical Phenomena
1
For a simple electron transfer reaction, the coupling of mass transfer and kinetics at the electrode surface is described by
A) relating the species flux and the current
B) equating the species concentration with the bulk concentration
C) Fick's second law
D) none of the above
A) relating the species flux and the current
B) equating the species concentration with the bulk concentration
C) Fick's second law
D) none of the above
A
2
In case of a rotating disc electrode (RDE), as per Levich equation, the diffusion layer thickness depends on kinematic viscosity ( ) as
A)
B)
C)
D)
A)
B)
C)
D)
3
In the derivation of the Warburg impedance equation, it is assumed that the following effects can be neglected
A) diffusion
B) convection
C) electromigration
D) none of the above
A) diffusion
B) convection
C) electromigration
D) none of the above
B,C
4
Consider the following reaction
. The concentration of A and B in bulk solution are equal. When a positive dc bias is applied (vs. OCP), under steady-state conditions, on the surface,
A) CA > CB
B) CA < CB
C) CA = CB
D) it could be any of the above depending on kinetic parameter values.
. The concentration of A and B in bulk solution are equal. When a positive dc bias is applied (vs. OCP), under steady-state conditions, on the surface,
A) CA > CB
B) CA < CB
C) CA = CB
D) it could be any of the above depending on kinetic parameter values.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
5
For a simple electron transfer reaction, with finite diffusion layer thickness (bounded Warburg impedance) the charge transfer resistance
A) increases with dc bias is increased from OCP
B) increases when dc bias is decreased from OCP
C) decreases when dc bias is increased from OCP
D) decreases when dc bias is decreased from OCP
A) increases with dc bias is increased from OCP
B) increases when dc bias is decreased from OCP
C) decreases when dc bias is increased from OCP
D) decreases when dc bias is decreased from OCP

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
6
The equation that describes Bounded Warburg impedance is
A)
B)
C)
D) none of the above
A)
B)
C)
D) none of the above

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
7
Under semi-infinite boundary conditions, for a simple electron transfer reaction, the concentration oscillations and current oscillations have a phase offset (in radians) of
A)
B) 0
C)
D)
A)
B) 0
C)
D)

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
8
CPE behavior may be expected when the electrode has
A) 2D heterogeneity only
B) 3D heterogeneity only
C) both 2D and 3D heterogeneity
D) none of the above
A) 2D heterogeneity only
B) 3D heterogeneity only
C) both 2D and 3D heterogeneity
D) none of the above

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
9
If CPE exponent is -1, the element is
A) inductor,
B) capacitor,
C) resistance
D) Warburg impedance
A) inductor,
B) capacitor,
C) resistance
D) Warburg impedance

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
10
Consider a porous electrode. Edc = 0 V vs. OCP, and there is no reaction. When an ac potential is applied, at the pore end (x = l),
A) potential gradient is zero
B) potential amplitude is zero
C) potential amplitude is Eac0
D) none of the above
A) potential gradient is zero
B) potential amplitude is zero
C) potential amplitude is Eac0
D) none of the above

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
11
Consider a system which exhibits CPE behavior. Given Rsol = 100 cm2, Rt = Rp = 200 cm2, and CPE parameters Y0 = 5×10-5 (rad s-1)1-n, n =0.8 , the equivalent capacitance as per Brug's formula is __________ F cm2 and as per Hsu & Mansfeld formula is _________ F cm2

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
12
According to empirical studies, when the CPE parameter Y0 increases, the value of n
A) increases
B) decreases
C) does not change
D) can either increase or decrease but will not remain the same.
A) increases
B) decreases
C) does not change
D) can either increase or decrease but will not remain the same.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
13
If a porous insulating film is present on an electrode surface, the film component may be modeled with a
A) capacitor in parallel with a resistor
B) simple resistor
C) capacitor in parallel with a series combination of resistor and Warburg impedance
D) a simple capacitor
A) capacitor in parallel with a resistor
B) simple resistor
C) capacitor in parallel with a series combination of resistor and Warburg impedance
D) a simple capacitor

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
14
In a film, two types of defects that are considered in point defect model are ________ (one word) and interstitial

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
15
As per PDM, cation interstitials are consumed at
A) metal-film interface
B) film-solution interface
C) both of the above
D) none of the above
A) metal-film interface
B) film-solution interface
C) both of the above
D) none of the above

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
16
During anion vacancy creation, the film thickness remains constant

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
17
PDM employs the following equation to describe mass transfer in the film
A) Fick's second law in one dimension
B) Fick's second law in two dimensions
C) Nernst Planck equation
D) Fromhold-Cook equation
A) Fick's second law in one dimension
B) Fick's second law in two dimensions
C) Nernst Planck equation
D) Fromhold-Cook equation

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
18
CPE can arise from the following distribution of time constants
A) normal
B) logarithmic
C) random
D) normal distribution of logarithmic
A) normal
B) logarithmic
C) random
D) normal distribution of logarithmic

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
19
If CPE exponent is 0, then the element is
A) inductor,
B) capacitor,
C) resistor
D) Warburg
A) inductor,
B) capacitor,
C) resistor
D) Warburg

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
20
A Temkin isotherm model will reduce to Langmuir isotherm when parameter "g" is _____

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
21
Levich equation can be used to estimate
A) diffusion layer thickness in an RDE
B) fluid boundary layer thickness in RDE
C) temperature boundary layer thickness in RDE
D) diffusivity of a reacting species
A) diffusion layer thickness in an RDE
B) fluid boundary layer thickness in RDE
C) temperature boundary layer thickness in RDE
D) diffusivity of a reacting species

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
22
For a simple electron transfer reaction, with finite diffusion layer thickness (bounded Warburg impedance) the polarization resistance
A) increases with dc bias is increased from OCP
B) increases when dc bias is decreased from OCP
C) decreases when dc bias is increased from OCP
D) decreases when dc bias is decreased from OCP
A) increases with dc bias is increased from OCP
B) increases when dc bias is decreased from OCP
C) decreases when dc bias is increased from OCP
D) decreases when dc bias is decreased from OCP

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
23
A simple electron transfer reaction, 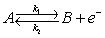 is conducted on a RDE.
is conducted on a RDE.
-Given that DA = DB, and CA-bulk = CB-bulk = 50 mM, if the concentration of A on the surface, CA-s = 20 mM at a given dc potential, then CB-s = _______ mM
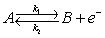 is conducted on a RDE.
is conducted on a RDE.-Given that DA = DB, and CA-bulk = CB-bulk = 50 mM, if the concentration of A on the surface, CA-s = 20 mM at a given dc potential, then CB-s = _______ mM

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
24
A simple electron transfer reaction, 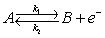 is conducted on a RDE.
is conducted on a RDE.
-In the above equation, if k1dc = 10-2 cm/s and k-1dc = 10-5 cm/s, then the net faradaic current is ______________ mA/cm2 . Remember that 1 M = 1 mol/lit = 10-3 mol/ cm3.
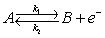 is conducted on a RDE.
is conducted on a RDE.-In the above equation, if k1dc = 10-2 cm/s and k-1dc = 10-5 cm/s, then the net faradaic current is ______________ mA/cm2 . Remember that 1 M = 1 mol/lit = 10-3 mol/ cm3.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
25
A simple electron transfer reaction with semi-infinite boundary conditions is analyzed using EIS. The polarization resistance of this system is
A) zero
B) infinity
C) finite positive value
D) finite negative value
A) zero
B) infinity
C) finite positive value
D) finite negative value

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
26
The complex plane plot of a simple electron transfer reaction acquired at multiple dc bias values is given below.
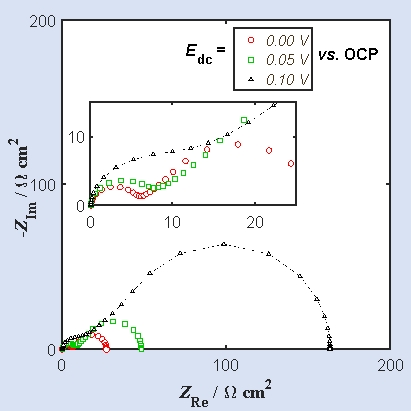 The low-frequency data shows the signature of
The low-frequency data shows the signature of
A) kinetic limited regime
B) semi-infinite Warburg
C) Bounded Warburg
D) constant phase element
 The low-frequency data shows the signature of
The low-frequency data shows the signature ofA) kinetic limited regime
B) semi-infinite Warburg
C) Bounded Warburg
D) constant phase element

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
27
Under semi-infinite boundary conditions, for a simple electron transfer reaction, the concentration oscillations and potential oscillations have a phase offset (in radians) of
A)
B)
C) 0
D)
A)
B)
C) 0
D)

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the following reaction
. The concentration of A and B in bulk solution are equal. When a negative dc bias is applied (vs. OCP), under steady-state conditions, on the surface,
A) CA > CB,
B) CA < CB
C) CA = CB
D) it could be any of the above depending on kinetic parameter values.
. The concentration of A and B in bulk solution are equal. When a negative dc bias is applied (vs. OCP), under steady-state conditions, on the surface,
A) CA > CB,
B) CA < CB
C) CA = CB
D) it could be any of the above depending on kinetic parameter values.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
29
A perfectly insulating film on an electrode surface is best modeled as a ________ (one word)

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
30
In the usual notation, the expression
is used to calculate
A) semi-infinite Warburg impedance
B) Bounded Warburg impedance
C) CPE impedance
D) porous electrode impedance
is used to calculate
A) semi-infinite Warburg impedance
B) Bounded Warburg impedance
C) CPE impedance
D) porous electrode impedance

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
31
PDM describes various processes that can occur in a film on the electrode surface. As per PDM, anion vacancies are produced at
A) metal-film interface
B) film-solution interface
C) both of the above
D) none of the above
A) metal-film interface
B) film-solution interface
C) both of the above
D) none of the above

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
32
As per PDM, the potential drop across metal-film interface depends on
A) film thickness
B) solution pH
C) both of the above
D) none of the above
A) film thickness
B) solution pH
C) both of the above
D) none of the above

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
33
PDM employs the following assumption to describe mass transfer within the film.
A) the film is a continuous medium
B) film is a lattice
C) film is porous
D) film has an accumulation of ions near interfaces.
A) the film is a continuous medium
B) film is a lattice
C) film is porous
D) film has an accumulation of ions near interfaces.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
34
When a film is present on an electrode surface, sometimes, an inductive loop at mid frequencies is seen in the complex plane plot of EIS data. This can be described using
A) PDM
B) SCA
C) AIC
D) all of the above
A) PDM
B) SCA
C) AIC
D) all of the above

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck



