Deck 10: Coordination Problems

Question 1

Consider the minimum effort coordination game, where players choose effort levels of 1 through 7 with everyone choosing 7 being the payoff dominant outcome and everyone choosing 1 being the secure outcome. Suppose the cost of effort increases from 0.25 to 0.75. We would expect:

A) a. More players to choose 1 (or lower numbers in general).
B) More players to choose 7 (or higher numbers in general).
C) More coordination to the payoff-dominant outcome.
D) More groups to coordinate to outcomes in the middle such as 3, 4 or 5.

Answer 1

a. More players to choose 1 (or lower numbers in general).

Question 2

A key difference between the stag-hunt game and the battle-of-the-sexes game is that:

A) the stag-hunt game has one payoff-dominant equilibrium and one risk-dominant equilibrium; the battle-of-the-sexes game has two equilibria, neither of which is either payoff or risk-dominant.
B) the battle-of-the-sexes game has one payoff-dominant equilibrium and one risk-dominant equilibrium; the stag-hunt game has two equilibria, none of which are either payoff or risk-dominant.
C) the battle-of-the-sexes game has one dominant strategy Nash equilibrium; the stag-hunt game has two equilibria, none of which are either payoff or risk-dominant.
D) the battle-of-the-sexes game has one payoff-dominant equilibrium and one risk-dominant equilibrium; the stag-hunt game has one dominant strategy Nash equilibrium.

Answer 2

the stag-hunt game has one payoff-dominant equilibrium and one risk-dominant equilibrium; the battle-of-the-sexes game has two equilibria, neither of which is either payoff or risk-dominant.

Question 3

Consider the following two player game. In this game:

A) There are two Nash equilibria: {Top, Left} and {Bottom, Right}.
B) There are two Nash equilibria: {Top, Right} and {Bottom, Left}.
C) There is a single dominant strategy Nash equilibrium: {Top, Left}
D) There is a single dominant strategy Nash Equilibrium: {Bottom, Right}

Answer 3

There are two Nash equilibria: {Top, Left} and {Bottom, Right}.

Question 4

Consider the following two player game. In this game:

A) {Top, Left} is the payoff dominant Nash equilibrium.
B) {Bottom, Right} is the payoff dominant Nash equilibrium.
C) There is a single dominant strategy Nash equilibrium: {Top, Left}
D) There is a single dominant strategy Nash Equilibrium: {Bottom, Right}

Question 5

The difference between a coordination problem and a prisoner's dilemma is that:

A) coordination problems have multiple equilibria while prisoner's dilemma games have one unique dominant strategy equilibrium.
B) prisoner's dilemma games have multiple equilibria while coordination problems game have one unique dominant strategy equilibrium.
C) coordination problems have multiple equilibria, one of which is payoff dominant, while prisoner's dilemma games have multiple equilibria which need not be payoff ranked.
D) prisoner's dilemma games have multiple equilibria, one of which is payoff dominant, while coordination problems have multiple equilibria which need not be payoff ranked.

Question 6

Consider the following two player game. In this game:

A) There are two Nash equilibria: {1, 1} and {2, 2}.
B) There are three Nash equilibria: {1, 1}, {2, 2} and (3, 3}.
C) There is a single dominant strategy Nash equilibrium: {3, 3}
D) There is a single dominant strategy Nash Equilibriu.: {2, 2}

Question 7

Consider the following two player game. In this game: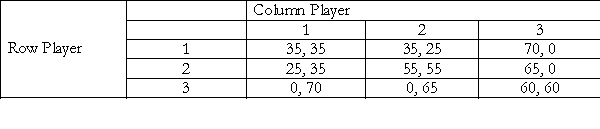

A) Strategy 3 is strictly dominated by both strategies 1, 2.
B) Strategy 3 is strictly dominated by strategy 1 but not by strategy 2.
C) Strategy 3 is strictly dominated by strategy 2 but not by strategy 1.
D) Strategy 3 is a strictly dominant strategy.

Question 8

In the Van Huyck et al. (1990) minimum effort game:

A) the payoff to a particular player is determined by his/her own effort and the minimum effort exerted by someone in the group.
B) the payoff to a particular player is determined by his/her own effort and the average effort exerted in the group.
C) groups typically find it quite easy to coordinate to the payoff dominant outcome.
D) the minimum is usually above 1 for much of the time.

Question 9

A key factor in coordinating to the payoff dominant outcome in minimum effort coordination games is:

A) the creation of optimistic beliefs about the effort choices of one's peers; even small degrees of uncertainty can lead to large coordination failures.
B) the presence of a strictly dominant strategy.
C) the presence of multiple dominated strategies.
D) that interactions must be anonymous and occur without any possibility of pre-play communication.

Question 10

Consider the following two player game. In this game: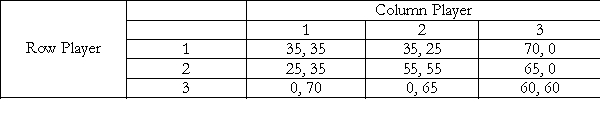

A) a. {2, 2} is the payoff dominant Nash equilibrium.
B) {1, 1} is the payoff dominant Nash equilibrium.
C) {3, 3} is the payoff dominant Nash equilibrium.
D) There is no payoff dominant strategy.

Question 11

Consider the following two player game. In this game:

A) {Top, Left} is the risk dominant outcome while {Bottom, Right} is the payoff dominant outcome.
B) {Top, Left} is the payoff dominant outcome while {Bottom, Right} is the risk dominant outcome.
C) There is a single dominant strategy Nash equilibrium: {Top, Left}
D) There is a single dominant strategy Nash Equilibrium: {Bottom, Right}

Question 12

Van Huyck et al. (1990) argue that the failure of many groups to coordinate to the payoff dominant equilibrium of everyone choosing "7" is caused by "strategic uncertainty". By this they mean that participants:

A) Are reluctant to choose high numbers because they are not absolutely convinced that everyone else in the group will do the same.
B) Are not certain that everyone else understands that the game has a dominant strategy, which is to always choose 1.
C) Are not certain that everyone else understood the payoff matrix.
D) Are not certain that everyone knows which strategy to choose in order to coordinate to the secure equilibrium.

Question 13

Brandts and Cooper, in their studies of the Corporate Turnaround Game, report that:

A) The degree of coordination success depends crucially on the amount of performance bonus for coordination; the larger the bonus the greater the coordination success.
B) The degree of coordination success depends on the payment of a performance bonus for coordination; but the actual magnitude of the bonus is immaterial. A small bonus has the same impact on coordination success as a large one.
C) Even the payment of a performance bonus does not manage to get all workers to consistently choose that strategy that leads to the payoff dominant equilibrium.
D) Once provided the explicit context of turning around a struggling company, workers easily coordinate to the payoff dominant equilibrium and there is no need for a performance bonus to improve coordination.

Question 14

Which of the following is an accurate summary of the results reported by Van Huyck et al. (1990)?

A) Most groups manage to coordinate to the payoff dominant equilibrium especially if they were given the opportunity to send messages to one another.
B) Most groups manage to coordinate to the payoff dominant equilibrium of everyone choosing "7" for some of the rounds but fail to sustain the coordination success for the entire session of 10 rounds.
C) Most groups manage to coordinate to the payoff dominant equilibrium of everyone choosing "7" for when given the opportunity to communicate but not in the absence of any communication among group members.
D) The highest minimum achieved by any group is "4" and the minimum never stayed above "1" for more than 3 rounds.

Question 15

In Cooper et al.'s study of the role of communication in the battle of the sexes game, the authors report that participants:

A) Never manage to achieve successful coordination with a very large proportion of disequilibrium outcomes.
B) Manage to achieve successful coordination to one of the two available equilibria as long as only one player made an announcement but failed to successfully coordinate when both players make an announcement; primarily because often the two players fail to announce a common strategy.
C) Manage to achieve successful coordination to one of the two available equilibria when both players have an opportunity to make an announcement but fail to achieve coordination when only one player makes an announcement.
D) Manage to achieve successful coordination when players are allowed to move in sequence with one following the other.

Question 16

Existing evidence suggests that coordination to the payoff dominant equilibrium is easier to achieve when:

A) participant groups are randomly re-matched from one round to the next rather than when group composition remains unchanged over time.
B) participant group composition remains unchanged over time as opposed to when groups are randomly re-matched from one round to the next.
C) Groups are larger rather than smaller.
D) participants are not allowed to communicate as opposed when communication is allowed.

Question 17

Evidence suggests that ___________ require _______________ in order to coordinate successfully, while __________ can achieve successful coordination even on the basis of ____________.

A) randomly re-matched groups; exhortative messages; fixed groups; financial incentives.
B) randomly re-matched groups; financial incentives; fixed groups; exhortative messages.
C) randomly re-matched groups; communication; fixed groups; no communication.
D) randomly re-matched groups; exhortative messages; fixed groups; no communication.

Question 18

Roberto Weber's study of intra-organization coordination suggests that it is possible to sustain coordination in large groups:

A) By allowing groups to grow slowly, typically by adding one member at a time and exposing new members to the prior history of interactions thereby acculturating them in the shared norms.
B) By adding multiple new group members at a time as long as there is a financial incentive in the form of a performance bonus for successful coordination.
C) By allowing groups to grow slowly, typically by adding one member at a time as long as there is a financial incentive in the form of a performance bonus for successful coordination.
D) By adding multiple new groups members at a time as long as the older group members are allowed to advise the new arrivals.

Question 19

In the study by Chaudhuri, Schotter and Sopher, a key component of successful coordination to the payoff dominant equilibrium is:

A) The availability of large financial incentives in the form of performance bonuses.
B) To allow groups to grow slowly by one member at a time.
C) The ability of participants to send private text messages to future generations of players.
D) The ability of participants to write advice for future generations of players and for this advice to be common knowledge among the recipients.

Question 20

The Chaudhuri, Schotter and Sopher results suggest that in order to successfully coordinate to the payoff dominant equilibrium:

A) All participants must be convinced that every other participant will choose "7"; even small amounts of doubt can lead to large-scale coordination failures.
B) All participants must be convinced that at least one other participant will chose "7".
C) All participants must first coordinate on sending the message that every person will choose "7" and then each participant must follow up by actually choosing "7".
D) All participants must first successfully eliminate all dominated strategies.

Question 21

Consider the following payoff matrix for a 2-player game where the payoffs have the usual connotation. The first number in each cell represents the payoff to Player #1 and the second number the payoff to Player #2.
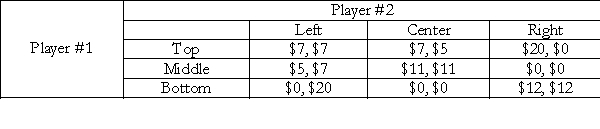(a) What is/are the Nash equilibrium/equilibria of this game? (b) Explain your answer very briefly. (c) Suppose the two players have each bought a ticket worth $8 to play this game. Both players know that the other player has paid $8.00 to play the game. How do you think the payment of this fee may change the equilibrium outcome of the game from one where no such fee is paid?

Question 22

(a) What do economists mean by "forward induction"? (b) Now consider the following minimum effort game from Van Huyck, Battalio and Beil (1990).
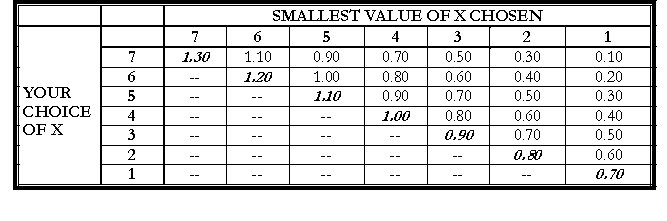(i) What typically happens to the minimum number chosen in the group when groups of subjects are asked to play this game? Why is the usual outcome surprising? (ii) Discuss, with an example (i.e. using numbers relevant to this payoff table), as to how a forward induction argument might help in solving the coordination problem in games like the one presented above.

Question 23

Consider the following two player game, where "a" through "h" are all greater than zero:

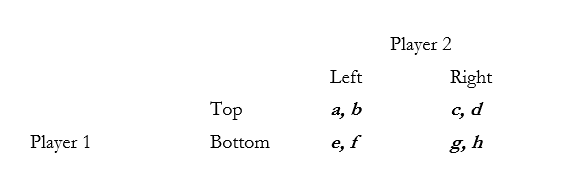
(a) What conditions must we impose on the values of a through h to make both {Top, Left} and {Bottom, Right} Nash equilibria of this game? (b) What additional conditions must we impose on the values of a through h to make {Top, Left} a payoff dominant Nash equilibrium?

Question 24

Explain clearly - using a numerical example in each case - the difference between (1) a prisoner's dilemma game; (2) a stag-hunt type coordination game and (3) a pure coordination game such as the battle-of-the-sexes. If your numerical examples are correct then that should provide most of the answer. I want you to briefly elaborate on how the equilibrium/equilibria in these games might differ and in what sense.

Question 25

Consider the following two games taken from Cooper, DeJong, Forsyth and Ross's paper. In each game the two players have three strategies - 1, 2 and 3.

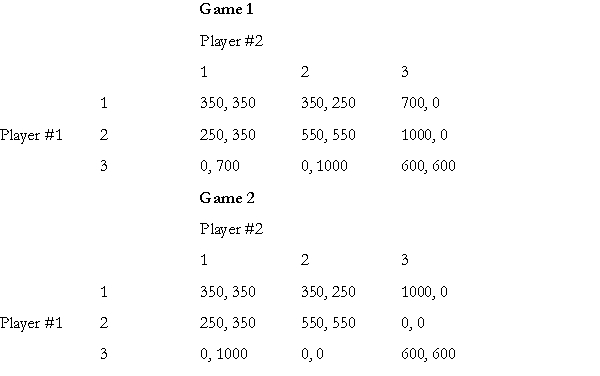
(a) What is (are) the Nash equilibrium/equilibria in Game 1 and Game 2? (b) Would you expect the outcomes in the two games to be similar or different? If different, then explain briefly, how they are different? (c) In discussing the outcomes of the two games, clearly relate your answer to the (i) concept of payoff dominance and (ii) the role of dominated strategies.

Question 26

Clearly identify the two components that are crucial to successful intra-organization coordination as groups grow larger over time in the study undertaken by Roberto Weber.