Deck 8: Torque and Angular Momentum
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/61
Play
Full screen (f)
Deck 8: Torque and Angular Momentum
1
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the Z-axis, perpendicular to the X-Y plane, is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .
.
2
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the -axis, perpendicular to the Z-Y plane, is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .
.
3
What is the rotational inertia of a solid iron disk of mass with a thickness of and radius of , about an axis perpendicular to the disk and passing through its center?
A)
B)
C)
D)
A)
B)
C)
D)
4
A mass is located at and a mass is located at ). The rotational inertia of this system of masses about the X-axis, perpendicular to the Z-Y plane, is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
5
A mass is located at and a mass is located at ). The rotational inertia of this system of masses about the Y-axis, perpendicular to the X-Z plane, is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
6
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the Z-axis, perpendicular to the plane, is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
7
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the X-axis, perpendicular to the Z-Y plane, is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
8
A mass is located at and a mass is located at , ). The rotational inertia of this system of masses about the Y-axis, perpendicular to the Z-X plane, is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
9
The rotational inertia of a thin rod about one end is . What is the rotational inertia of the same rod about a point located from the end?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
10
The rotational inertia of a thin rod about one end is . What is the rotational inertia of the same rod about a point located from the end?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
11
A wrench is used to generate a torque at a bolt. A force of is applied perpendicularly at the end of the wrench. The torque generated at the bolt is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
12
A wrench is used to generate a torque at a bolt. A force of is applied at the end of the wrench at an angle of 70.0 degrees. The torque generated at the bolt is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
13
A torque of is applied to a bolt. The bolt rotates through an angle of 180 degrees. The work done in turning the bolt is
A) .
B) .
C) .
D) .
E)
A) .
B) .
C) .
D) .
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
14
A torque of is applied to a bolt. The bolt rotates through an angle of 360 degrees. The work done in turning the bolt is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
15
A mass is located at and a mass is located at , ). The center of gravity of the system of masses is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
16
A mass is located at and a mass is located at , ). The center of gravity of the system of masses is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
17
A mass is located at ( and a mass is located at , ). The center of gravity of the system of masses is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
18
A mass is located at , a mass is located at , and a mass is located at . The center of gravity of the system of masses is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
19
A mass is located at , a mass is located at , and a mass is located at . The center of gravity of the system of masses is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
20
A long uniform beam of mass is supported by a wire as shown in the figure. The beam makes an angle of 10.00 degrees with the horizontal and the wire makes an angle of 30.00 degrees with the beam. A mass, , is attached to the end of the beam. What is the tension in the wire?
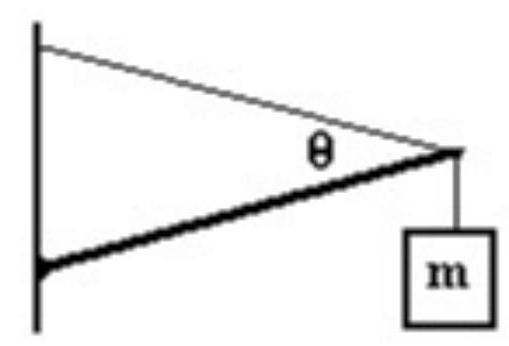
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
21
A long uniform beam of mass is supported by a wire as shown in the figure. The beam makes an angle of 10.00 degrees with the horizontal and the wire makes an angle of 30.00 degrees with the beam. A mass, , is attached to the end of the beam. What are the vertical and horizontal components of the force of the wall on the beam at the hinge?
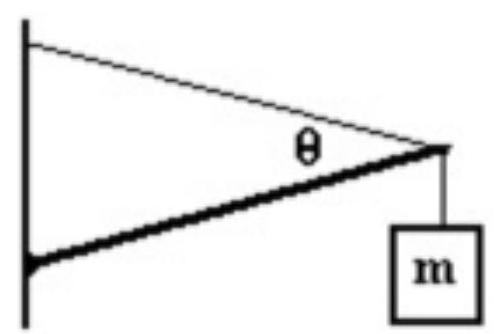
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
22
A ladder that is long is placed against a wall at an angle theta. The center of gravity of the ladder is at a point from the base of the ladder. The coefficient of static friction at the base of the ladder is 0.800 . There is no friction between the wall and the ladder. What is the vertical force of the ground on the ladder?
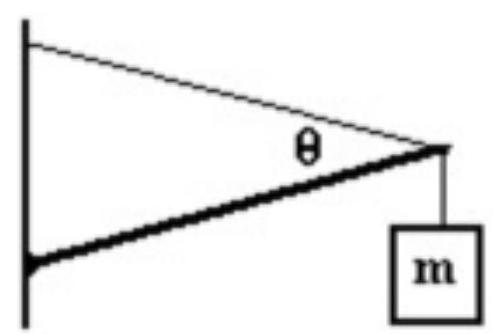
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
23
A ladder that is long is placed against a wall at an angle theta. The center of gravity of the ladder is at a point from the base of the ladder. The coefficient of static friction at the base of the ladder is 0.800 . There is no friction between the wall and the ladder. What is the minimum angle the ladder must make with the horizontal for the ladder not to slip and fall?
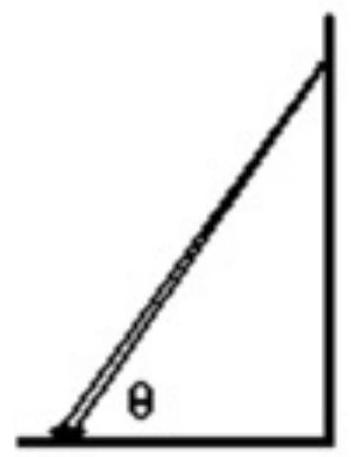
A) 40.55 degrees
B) 30.34 degrees
C) 26.57 degrees
D) 36.35 degrees
E) 46.52 degrees

A) 40.55 degrees
B) 30.34 degrees
C) 26.57 degrees
D) 36.35 degrees
E) 46.52 degrees

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
24
A ladder that is long is placed against a wall at an angle theta. The center of gravity of the ladder is at a point from the base of the ladder. The coefficient of static friction at the base of the ladder is 0.400 . There is no friction between the wall and the ladder. What is the minimum angle the ladder must make with the horizontal for the ladder not to slip and fall?
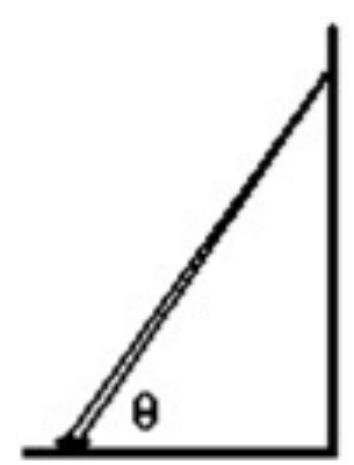
A) 35 degrees
B) 53 degrees
C) 45 degrees
D) 60 degrees
E) 65 degrees

A) 35 degrees
B) 53 degrees
C) 45 degrees
D) 60 degrees
E) 65 degrees

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
25
A object has a moment of inertia of . If a torque of is applied to the object, the angular acceleration is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
26
A object has a moment of inertia of . What torque is needed to give the object an angular acceleration of ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
27
A sphere with a radius has a moment of inertia of . If a torque of is applied to the object, the angular acceleration is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
28
An object has a moment of inertia of . If a torque of is applied to the object, the angular acceleration is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
29
A object has a moment of inertia of . What torque is needed to give the object an angular acceleration of ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
30
A solid cylinder with a radius has a moment of inertia of . If a torque of is applied to the object, the angular acceleration is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
31
A torque of is applied to a object to give it an angular acceleration. If the angular acceleration is , then the moment of inertia is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
32
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the downward acceleration of ?
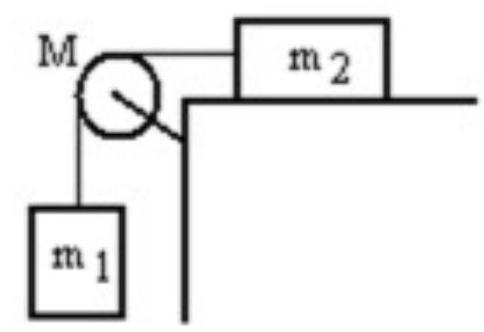
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
33
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the tension in the string attached to ?
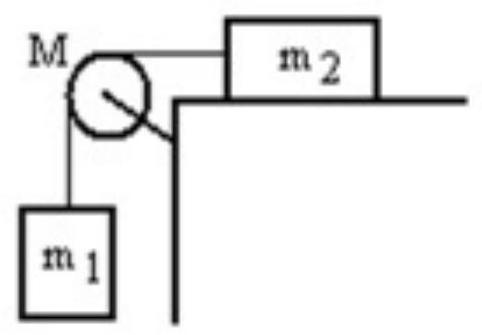
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
34
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the tension in the string attached to ?
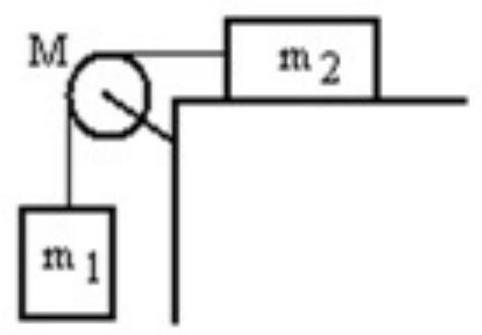
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
35
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and is , then what is the downward acceleration of ?
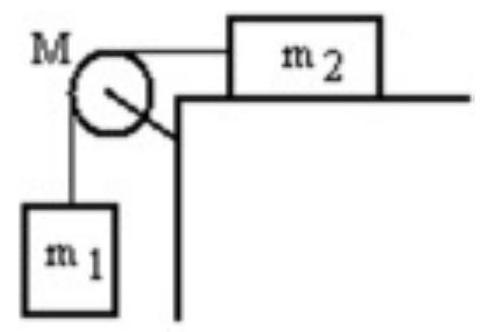
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
36
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and is , then what is the downward acceleration of ?
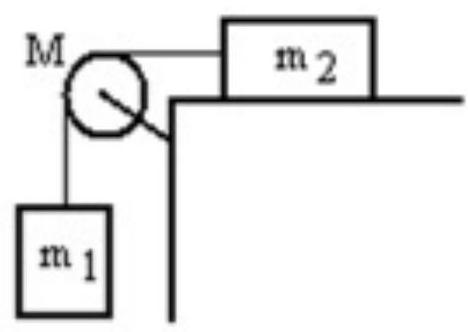
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
37
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the tension in the string attached to ?
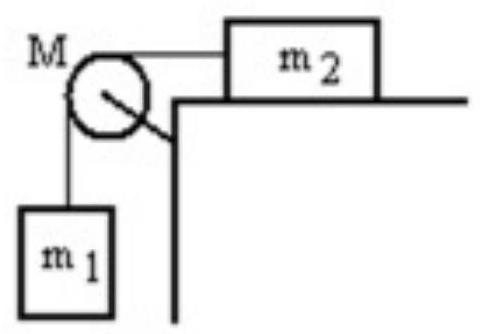
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
38
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless horizontal surface as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is , and M is , then what is the tension in the string attached to ?
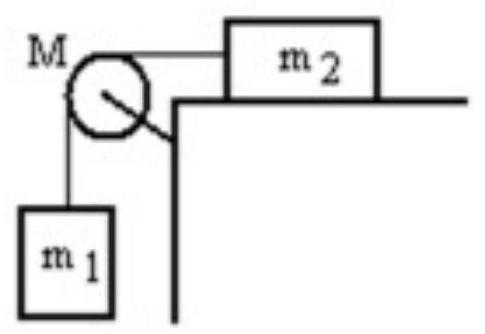
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
39
A mass is connected by a light string that passes over a pulley of mass to a mass as shown in the figure. Both masses move vertically and there is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is and is , then what is the magnitude of the acceleration of the masses?
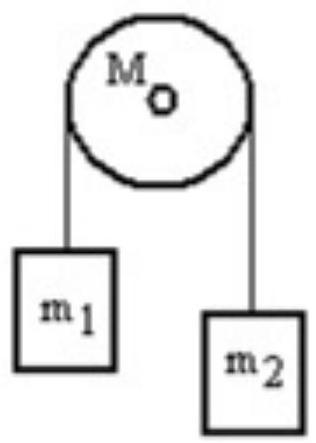
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
40
A mass is connected by a light string that passes over a pulley of mass to a mass as shown in the figure. Both masses move vertically and there is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is and is , then what is the tension in the string that is attached to ?
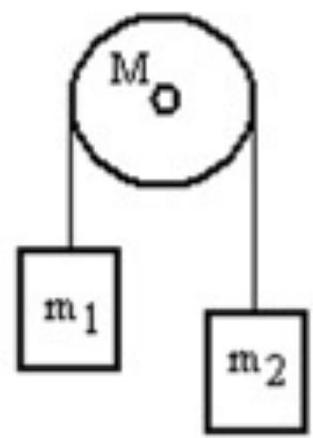
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
41
A mass is connected by a light string that passes over a pulley of mass to a mass as shown in the figure. Both masses move vertically and there is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is and is , then what is the tension in the string that is attached to ?
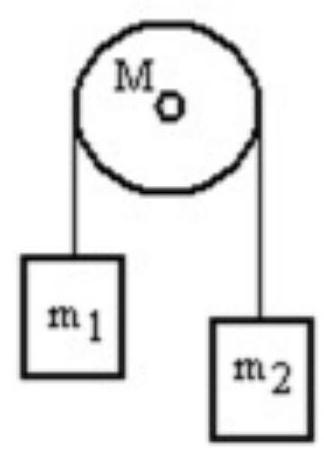
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
42
A mass is connected by a light string that passes over a pulley of mass to a mass as shown in the figure. Both masses move vertically and there is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is and is , then what is the magnitude of the acceleration of the masses?
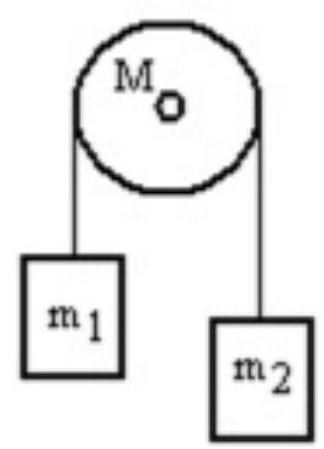
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
43
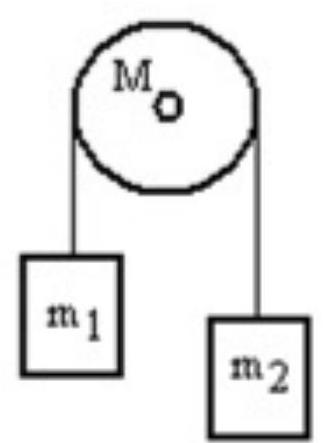
A mass is connected by a light string that passes over a pulley of mass to a mass as shown in the figure. Both masses move vertically and there is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is and is , then what is the tension in the string that is attached to mass ?
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
44
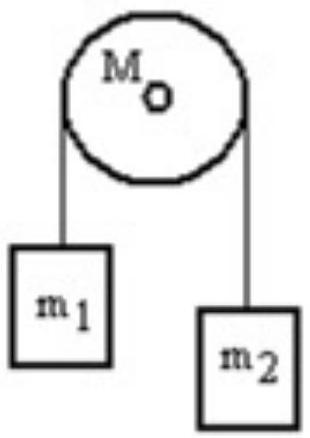
A mass is connected by a light string that passes over a pulley of mass to a mass as shown in the figure. Both masses move vertically and there is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is and is , then what is the tension in the string that is attached to mass ?
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
45
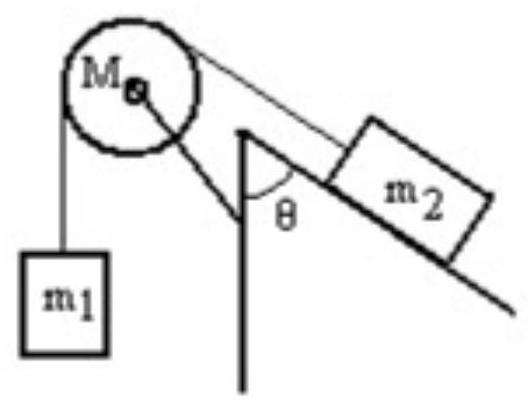
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless incline as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is is , and the angle is 60.0 degrees, then what is the acceleration of ?
A) down
B) down
C) down
D) down
E) down

A) down
B) down
C) down
D) down
E) down

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
46
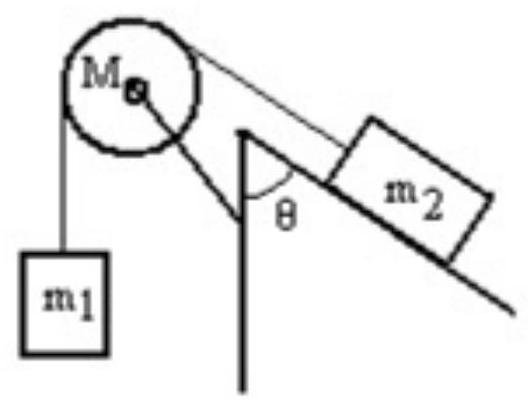
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless incline as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is is , and the angle is 60.0 degrees, then what is the acceleration of ?
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
47
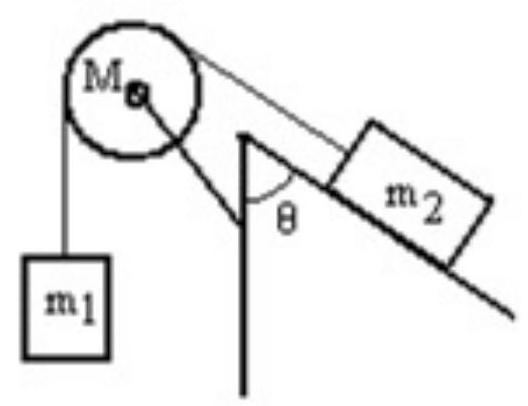
A mass is connected by a light string that passes over a pulley of mass to a mass sliding on a frictionless incline as shown in the figure. There is no slippage between the string and the pulley. The pulley has a radius of and a moment of inertia of . If is is is , and the angle is 70.0 degrees, then what is the acceleration of ?
A) down
B) down
C) down
D) down
E) down

A) down
B) down
C) down
D) down
E) down

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
48
A solid sphere ( is spinning with an angular velocity of . The diameter of the sphere is . The rotational kinetic energy of the spinning sphere is
A) .
B) .
C) .
D) .
E)
A) .
B) .
C) .
D) .
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
49
A hollow cylinder has a diameter of . The cylinder is rolling down a hill with a velocity of . The rotational kinetic energy of the rolling cylinder is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
50
A hollow sphere is spinning with an angular velocity of . The diameter of the sphere is . The rotational kinetic energy of the spinning sphere is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
51
A hollow sphere of radius starts from rest and rolls without slipping down a 30.0 degree incline. The acceleration of the center of mass of the hollow sphere is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
52
A hollow cylinder of radius starts from rest and rolls without slipping down a 30.0 degree incline. The acceleration of the center of mass of the cylinder is
A) .
B) .
C)
D) .
E) .
A) .
B) .
C)
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
53
A hollow cylinder of radius starts from rest and rolls without slipping down a 30.0 degree incline. If the length of the incline is , then the velocity of the center of mass of the cylinder at the bottom of the incline is
A) .
B) .
C) .
D) .
E)
A) .
B) .
C) .
D) .
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
54
A solid sphere of radius starts from rest and rolls without slipping down a 30.0 degree incline. The acceleration of the center of mass of the solid sphere is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
55
A solid sphere with a diameter of is rotating at an angular velocity of 5.0 . The angular momentum of the rotating sphere is
A) .
B) .
C) .
D) .
E) .
A) .
B) .
C) .
D) .
E) .

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
56
A grinding wheel has a mass of and moment of inertia of . A torque of is applied to the grinding wheel. If the wheel starts from rest, what is the angular momentum of the wheel after 5.0 seconds?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
57
A 1.5m long dowel (a cylindrical rod) is pivoted about the end so that it is a pendulum of sorts - it can freely swing in a vertical plane. The dowel has a diameter of , and its density is . When it is positioned in its swing such that its angle with the vertical is 22.5 degrees, what is the torque on the rod about the pivot due to its weight?
A)
B)
C)
D)
E)
F)
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
58
A long, dowel is pivoted about the end so that it is a pendulum of sorts - it can freely swing in a vertical plane. At the other end of the dowel is a brass weight having mass . (The center of the brass weight is from the pivot point.) When the rod is positioned in its swing such that its angle with the vertical is 22.5 degrees, what is the net torque on the rod about the pivot?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
59
A girl swings on a swing, whose seat is attached to the pivot by long rigid rods (considered to be massless in this problem). As she swings, she rises to a maximum height such that the angle of the rods with respect to the vertical is 32 degrees. What is the maximum torque on the rods due to her weight, as she moves during one cycle of her swinging from the bottom of her swing path to the highest point?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
60
A solid disk spins at . A torque of is applied for to bring it to rest. What is the disk's radius?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck
61
A person rides a bicycle along a straight road. From the point of view of the rider, what's the direction of the angular momentum vector of the front wheel?
A) left
B) up
C) down
D) backward
E) forward
F) right
A) left
B) up
C) down
D) backward
E) forward
F) right

Unlock Deck
Unlock for access to all 61 flashcards in this deck.
Unlock Deck
k this deck



