Deck 6: Frequency Response

Question 1

A common-source amplifier is fed from a signal source having a resistance $R_{\mathrm{sig}}=100 \mathrm{k} \Omega$ and has a load resistance $R_{L}=100 \mathrm{k} \Omega$ . The MOSFET has $C_{g s}=0.1 \mathrm{pF}, C_{g d}=50 \mathrm{fF}, g_{m}=1 \mathrm{~mA} / \mathrm{V}$ , and $r_{o}=$ $100 \mathrm{k} \Omega$ . The total capacitance between the output node and ground is $C_{L}=0.1 \mathrm{pF}$ .
(a) Find the midband gain.
(b) Use the method of open-circuit time constants to obtain an estimate of the upper 3-dB frequency, $f_{H}$ .

Answer 1

Refer to Figure 10.1.1


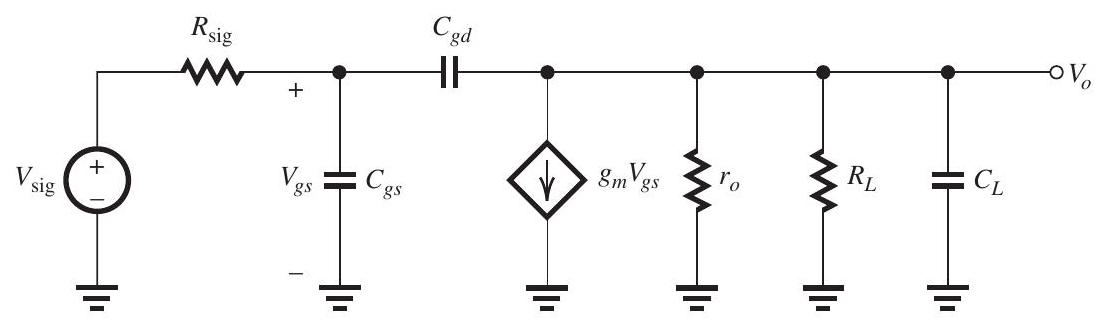
Figure 10.1.1
(a) At midband frequencies,
$$\begin{aligned}\frac{V_{o}}{V_{\text {sig }}} & =-g_{m}\left(r_{o} \| R_{L}\right) \\& =-1 \times(100 \| 100) \\& =-50 \mathrm{~V} / \mathrm{V}\end{aligned}$$
(b) Capacitor $C_{g s}$ sees a resistance
$$R_{g_{s}}=R_{\mathrm{sig}}=100 \mathrm{k} \Omega$$
Thus,
$$\begin{aligned}\tau_{g s} & =C_{g s} R_{g s} \\& =0.1 \times 10^{-12} \times 100 \times 10^{3} \\& =10 \mathrm{~ns}\end{aligned}$$
Capacitor $C_{g d}$ sees a resistance
$$R_{g d}=R_{L}^{\prime}+R_{\text {sig }}\left(1+g_{m} R_{L}^{\prime}\right)$$
where
$$R_{L}^{\prime}=r_{o}\left\|R_{L}=100\right\| 100=50 \mathrm{k} \Omega$$
Thus,
$$\begin{aligned}R_{g d} & =50+100 \times(1+1 \times 50) \\& =5150 \mathrm{k} \Omega\end{aligned}$$
and
$$\begin{aligned}\tau_{g d} & =C_{g d} R_{g d} \\& =50 \times 10^{-15} \times 5150 \times 10^{3} \\& =257.5 \mathrm{~ns}\end{aligned}$$
Capacitor $C_{L}$ sees a resistance
$$R_{C L}=R_{L}\left\|r_{O}=100\right\| 100=50 \mathrm{k} \Omega$$
Thus,
$$\begin{aligned}\tau_{C L} & =C_{L} R_{C L} \\& =0.1 \times 10^{-12} \times 50 \times 10^{3} \\& =5 \mathrm{~ns}\end{aligned}$$
Finally,
$$\begin{aligned}\tau_{H} & =\tau_{g s}+\tau_{g d}+\tau_{C L} \\& =10+257.5+5 \\& =272.5 \mathrm{~ns}\end{aligned}$$
and
$$\begin{aligned}f_{H} & =\frac{1}{2 \pi \tau_{H}}=\frac{1}{2 \pi \times 272.5 \times 10^{-9}} \\& =584 \mathrm{kHz}\end{aligned}$$

Question 2

(a) Sketch the high-frequency equivalent circuit of a common-emitter amplifier that is fed with a voltage signal source $V_{\text {sig }}$ having a resistance $R_{\text {sig }}$ and that is loaded with a resistance $R_{L}$ . In addition to the internal capacitances of the BJT, $C_{\pi}$ and $C_{\mu}$ , there is a capacitance $C_{L}$ between the output node and ground.
(b) If the transistor is biased at $I_{C}=0.1 \mathrm{~mA}$ and has $\beta=100, V_{A}=40 \mathrm{~V}, f_{T}=500 \mathrm{MHz}$ , and $C_{\mu}=$ $0.27 \mathrm{pF}$ , find the values of $g_{m}, r_{\pi}, r_{o}$ , and $C_{\pi}$ .
(c) Use the method of open-circuit time-constants to obtain an estimate for the upper 3-dB frequency, $f_{H}$ , for the case $R_{\text {sig }}=25 \mathrm{k} \Omega, R_{L}=25 \mathrm{k} \Omega$ , and $C_{L}=0.5 \mathrm{pF}$ . Also, find the midband gain.

Answer 2

(a) The high-frequency equivalent circuit is shown in Fig. 10.2.1 below.


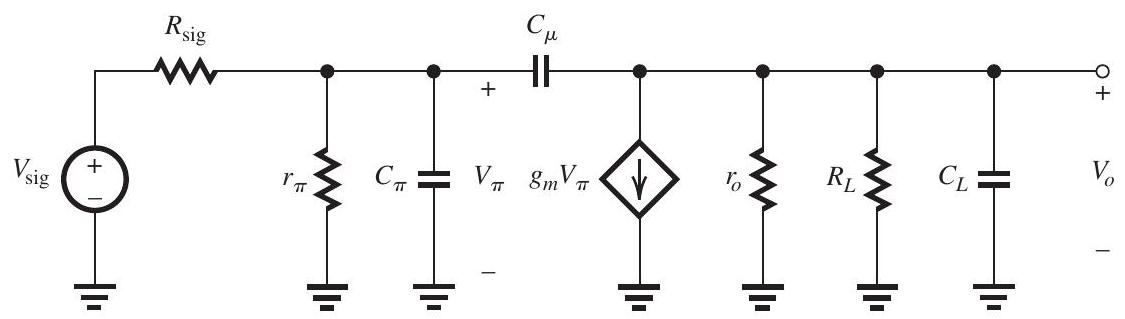
Figure 10.2.1
(b)
$$\begin{aligned}I_{C} & =0.1 \mathrm{~mA}, \quad \beta=100, \quad V_{A}=40 \mathrm{~V} \\f_{T} & =500 \mathrm{MHz}, \quad C_{\mu}=0.27 \mathrm{pF} \\g_{m} & =\frac{I_{C}}{V_{T}}=\frac{0.1}{0.025}=4 \mathrm{~mA} / \mathrm{V} \\r_{\pi} & =\frac{\beta}{g_{m}}=\frac{100}{4}=25 \mathrm{k} \Omega \\r_{o} & =\frac{V_{A}}{I_{C}}=\frac{40}{0.1}=400 \mathrm{k} \Omega \\C_{\pi}+C_{\mu} & =\frac{g_{m}}{\omega_{T}}=\frac{4 \times 10^{-3}}{2 \pi \times 500 \times 10^{6}}=1.27 \mathrm{pF} \\\Rightarrow C_{\pi} & =1 \mathrm{pF}\end{aligned}$$
(c) Capacitor $C_{\pi}$ sees a resistance $R_{\pi}$
$$\begin{aligned}R_{\pi} & =r_{\pi} \| R_{\text {sig }} \\& =25 \| 25 \\& =12.5 \mathrm{k} \Omega\end{aligned}$$
Capacitor $C_{\mu}$ sees a resistance $R_{\mu}$ ,
$$R_{\mu}=R_{L}^{\prime}+R_{\text {sig }}^{\prime}\left(1+g_{m} R_{L}^{\prime}\right)$$
where
$$\begin{aligned}R_{L}^{\prime} & =R_{L}\left\|r_{o}=25\right\| 400=23.5 \mathrm{k} \Omega \\R_{\text {sig }}^{\prime} & =R_{\text {sig }} \| r_{\pi} \\& =25 \| 25=12.5 \mathrm{k} \Omega\end{aligned}$$
Thus,
$$\begin{aligned}R_{\mu} & =23.5+12.5(1+4 \times 23.5) \\& =1211 \mathrm{k} \Omega\end{aligned}$$
Capacitor $C_{L}$ sees a resistance $R_{L}^{\prime}$ ,
$$R_{L}^{\prime}=R_{L}\left\|r_{O}=25\right\| 400=23.5 \mathrm{k} \Omega$$
Now,
$$\begin{aligned}\tau_{H}= & C_{\pi} R_{\pi}+C_{\mu} R_{\mu}+C_{L} R_{L}^{\prime} \\= & 1 \times 10^{-12} \times 12.5 \times 10^{3}+0.27 \times 10^{-12} \\& \times 1211 \times 10^{3}+0.5 \times 10^{-12} \times 23.5 \times 10^{3} \\= & 12.5 \times 10^{-9}+327 \times 10^{-9}+11.75 \times 10^{-9} \\= & 351.2 \mathrm{~ns} \\f_{H}= & \frac{1}{2 \pi \tau_{H}}=\frac{1}{2 \pi \times 351.2 \times 10^{-9}} \\= & 453 \mathrm{kHz} \\A_{M}= & \frac{V_{o}}{V_{\text {sig }}}=\frac{r_{\pi}}{r_{\pi}+R_{\text {sig }}} \times-g_{m} R_{L}^{\prime} \\= & \frac{25}{25+25} \times-4 \times 23.5 \\= & -47 \mathrm{~V} / \mathrm{V}\end{aligned}$$

Question 3

(a) An NMOS common-source amplifier with a simple PMOS current-source load has a total capacitance at the output node of $C_{L}=10 \mathrm{pF}$ . If the resistance of the signal source is very small, find the dc gain, the 3-dB frequency, and the gainbandwidth product, provided that $g_{m}=1 \mathrm{~mA} / \mathrm{V}$ and $r_{O}=20 \mathrm{k} \Omega$ for each of the two transistors.
(b) If, in the circuit in (a), a cascode transistor is added to both the amplifier and the current-source load, find the new values of the $\mathrm{dc}$ gain, $f_{3 \mathrm{~dB}}$ , and the gain-bandwidth product. Assume that all transistors have the same $g_{m}$ and $r_{o}$ as in (a) and that the total capacitance at the output node remains unchanged.

Answer 3

(a)


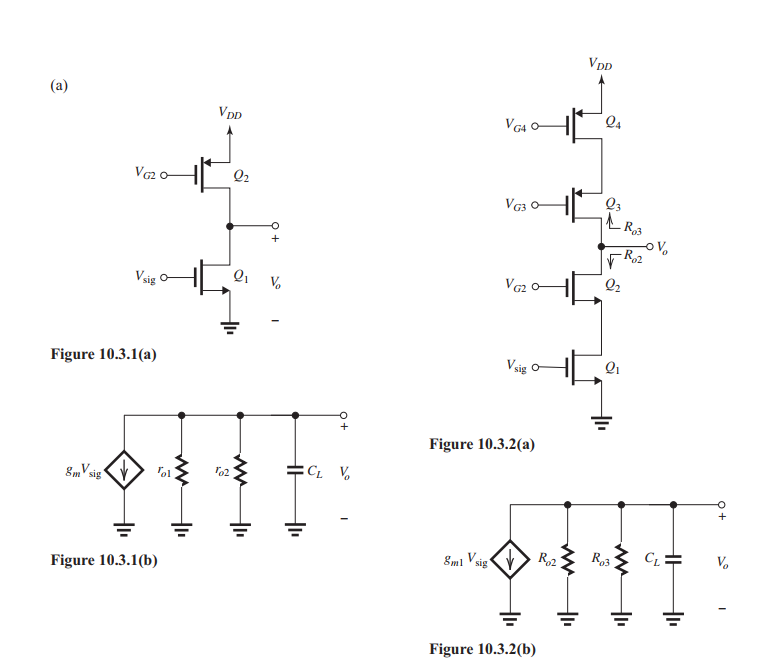
Figure 10.3.1 shows the amplifier together with its output equivalent circuit. The dc gain is given by
$$\begin{aligned}\frac{V_{o}}{V_{\text {sig }}} & =-g_{m}\left(r_{o 1} \| r_{o 2}\right) \\& =-g_{m}\left(r_{o} \| r_{o}\right)=-\frac{1}{2} g_{m} r_{o} \\& =-\frac{1}{2} \times 1 \times 20=-10 \mathrm{~V} / \mathrm{V}\end{aligned}$$
The 3-dB frequency is determined from the equivalent circuit as
$$\begin{aligned}f_{3 d B} & =\frac{1}{2 \pi C_{L}\left(r_{O 1} \| r_{O 2}\right)} \\& =\frac{1}{2 \pi C_{L} \times \frac{1}{2} \times r_{O}} \\& =\frac{1}{\pi \times 10 \times 10^{-12} \times 20 \times 10^{3}} \\& =1.6 \mathrm{MHz} \\\mathrm{GB} & =10 \times 1.6=16 \mathrm{MHz}\end{aligned}$$
(b)
Figure 10.3.2 shows the cascode amplifier together with its output equivalent circuit. The dc gain is given by
$$\frac{V_{o}}{V_{\text {sig }}}=-g_{m 1}\left(R_{o 2} \| R_{o 3}\right)$$
where
$$\begin{aligned}& g_{m 1}=g_{m}=1 \mathrm{~mA} / \mathrm{V} \\& R_{o 2}=R_{o 3}=\left(g_{m} r_{o}\right) r_{o}=(1 \times 20) \times 20=400 \mathrm{k} \Omega\end{aligned}$$
Thus,
$$\frac{V_{o}}{V_{\text {sig }}}=-1 \times(400 \| 400)=-200 \mathrm{~V} / \mathrm{V}$$
The 3-dB frequency is determined from the equivalent circuit as
$$\begin{aligned}f_{3 d B} & =\frac{1}{2 \pi C_{L}\left(R_{O 2} \|\left(R_{O 3}\right)\right.} \\& =\frac{1}{2 \pi \times 10 \times 10^{-12} \times(400 \| 400) \times 10^{3}} \\& =80 \mathrm{kHz} \\\mathrm{GB} & =200 \times 80 \times 10^{3}=16 \mathrm{MHz}\end{aligned}$$

Question 4

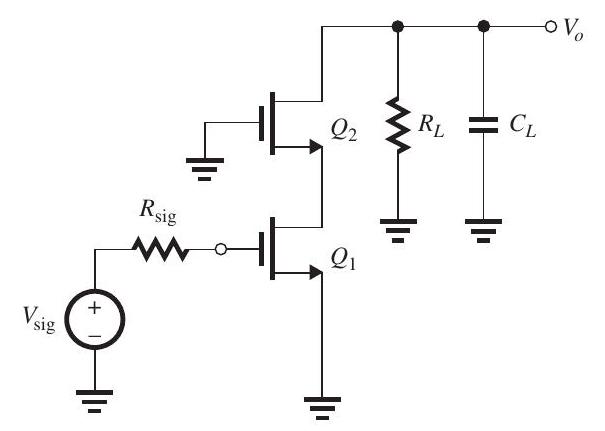
Figure 10.4.1
For the cascode amplifier in Fig. 10.4.1 (with the dc bias circuitry not shown), $g_{m 1}=g_{m 2}=$ $2.5 \mathrm{~mA} / \mathrm{V}, r_{o 1}=r_{o 2}=20 \mathrm{k} \Omega, C_{g s 1}=C_{g s 2}=$ $20 \mathrm{fF}, C_{g d 1}=C_{g d 2}=5 \mathrm{fF}, C_{d b 1}=C_{d b 2}=5 \mathrm{fF}$ , $C_{L}=5 \mathrm{fF}$ , and $R_{\mathrm{sig}}=10 \mathrm{k} \Omega$ . Investigate two designs, one that results in a de gain of $60 \mathrm{~dB}$ and one that provides a dc gain of $40 \mathrm{~dB}$ . For each case, find the required value of $R_{L}$ , the resulting 3 -dB frequency $f_{H}$ , and the gain-bandwidth product. Comment on the tradeoff between gain and bandwidth.

Question 5

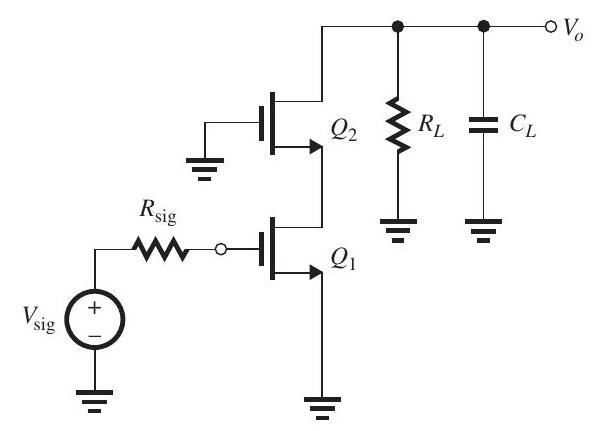
Figure 10.5.1


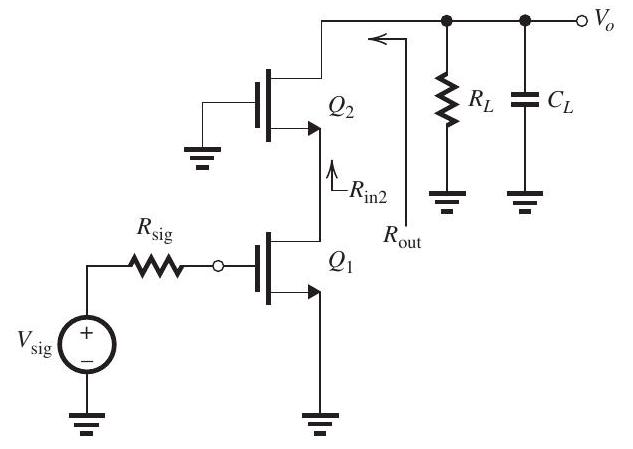
Figure 10.5.2
(a) The MOSFET in the common-source amplifier in Fig. 10.5.1, where the dc bias arrangement is not shown, is operating at $g_{m}=2 \mathrm{~mA} / \mathrm{V}$ and $r_{o}=20 \mathrm{k} \Omega$ and has $R_{\text {sig }}=R_{L}=20 \mathrm{k} \Omega$ . The transistor capacitances are specified as $C_{g s}=40 \mathrm{fF}$ and $C_{g d}=C_{d b}=10 \mathrm{fF}$ . Also, there is an additional capacitance between the output node and ground, $C_{L}=10 \mathrm{fF}$ . Find the overall de gain $G_{v} \equiv V_{o} / V_{\text {sig }}$ , the upper 3-dB frequency $f_{H}$ , and the gain-bandwidth product $f_{t}$ . To determine $f_{H}$ , use the method of open-circuit time constants and recall that the resistance seen by $C_{g d}$ is given by $R_{g d}=\left(1+g_{m} R_{L}^{\prime}\right) R_{\text {sig }}+R_{L}^{\prime}$ , where $R_{L}^{\prime}=R_{L} \| r_{o}$ .
(b) To increase $f_{t}$ , the common-source transistor $Q_{1}$ is cascoded as shown in Fig. 10.5.2 (refer to Figure above), where the dc bias arrangement is not shown. For the same values of $R_{\mathrm{sig}}, R_{L}$ , and $C_{L}$ as in (a), assuming $Q_{1}$ and $Q_{2}$ are biased so that $g_{m 1}=g_{m 2}=2 \mathrm{~mA} / \mathrm{V}$ and $r_{o 1}=r_{o 2}=20 \mathrm{k} \Omega$ , and for the capacitances of $Q_{1}$ and $Q_{2}$ to have the same values as specified in (a) above, find $G_{v}, f_{H}$ , and $f_{t}$ for the cascode amplifier. Recall that $R_{\text {out }} \simeq\left(g_{m} r_{o}\right) r_{o}$ and $R_{\text {in } 2}=\frac{1}{g_{m 2}}+\frac{R_{L}}{g_{m 2} r_{o 2}}$ .
In using the open-circuit time-constants method, adapt the formula given in (a) for $R_{g d}$ to obtain $R_{g d 1}$ . By what factor is $f_{t}$ increased?

Question 6

The MOSFET in the common-source amplifier in Fig. 10.6.1


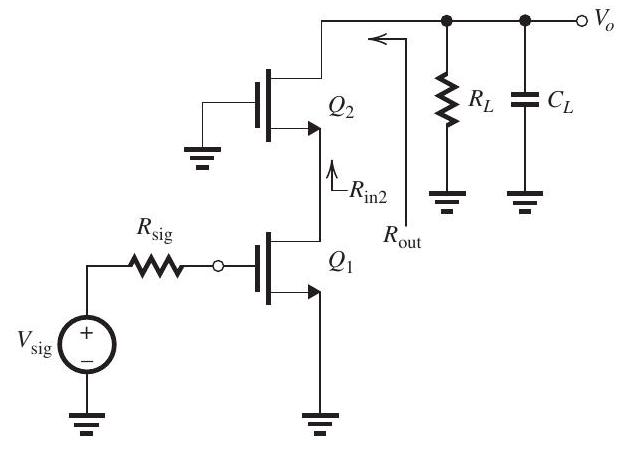
Figure 10.6.1
has $g_{m}=$ $5 \mathrm{~mA} / \mathrm{V}, r_{o}=20 \mathrm{k} \Omega, C_{g s}=5 \mathrm{pF}$ , and $C_{g d}=1 \mathrm{pF}$ , and the total capacitance at the output node, $C_{L}$ , is $10 \mathrm{pF}$ .
(a) Find the value of the midband voltage gain.
(b) Use the method of short-circuit time constants to determine the lower 3-dB frequency, $f_{L}$ . Which capacitor dominates the determination of $f_{L}$ ?
(c) Use the method of open-circuit time constants to determine the upper 3-dB frequency, $f_{H}$ . Which capacitor dominates the determination of $f_{H}$ ?

Question 7

The amplifier in Fig. 10.7.1


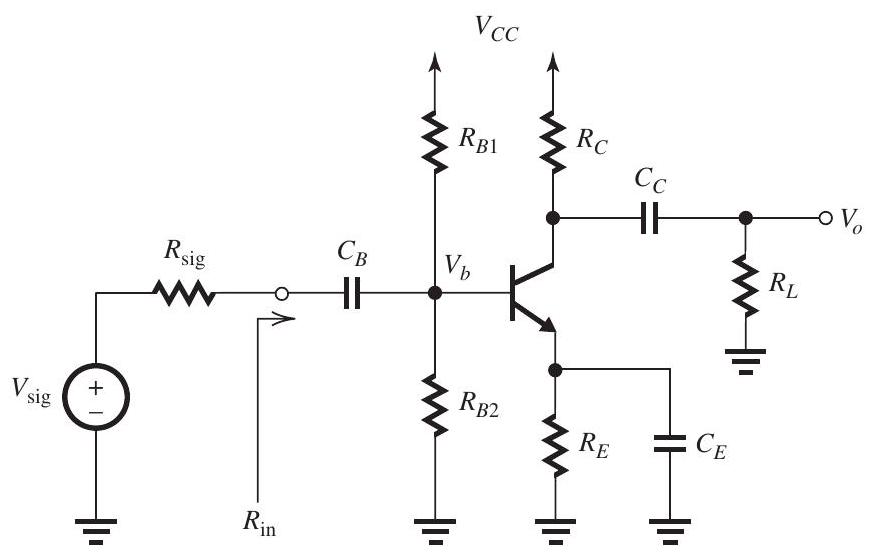
Figure 10.7.1
has $R_{\text {sig }}=1 \mathrm{k} \Omega, C_{B}=1 \mu \mathrm{F}, C_{E}=10$ $\mu \mathrm{F}, C_{C}=1 \mu \mathrm{F}, R_{L}=8 \mathrm{k} \Omega, V_{B E}=0.7 \mathrm{~V}$ , and $V_{C C}=15 \mathrm{~V}$ .
(a) Assuming $\beta=\infty$ , find $R_{B 1}, R_{B 2}, R_{E}$ , and $R_{C}$ to operate the BJT at a dc bias point characterized by $I_{C}=1 \mathrm{~mA}$ and $V_{C}=7 \mathrm{~V}$ . Design for $V_{B}=5 \mathrm{~V}$ and a voltage-divider current of $0.1 \mathrm{~mA}$ .
(b) Find $r_{e}, g_{m}$ , and $r_{\pi}$ , assuming $\beta=100$ .
(c) At midband frequencies, find $R_{\text {in }}, V_{b} / V_{\text {sig }}$ , $V_{o} / V_{b}$ , and $V_{o} / V_{\text {sig }}$ , assuming $\beta=100$ .
(d) In the low-frequency band use the method of short-circuit time constants to obtain an estimate of the 3-dB frequency, $f_{L}$ .
(e) If $C_{\pi}=10 \mathrm{pF}$ and $C_{\mu}=1 \mathrm{pF}$ , use the Miller approximation to determine the input capacitance of the amplifier at high frequencies, and hence determine an estimate of the high-frequency $3 \mathrm{~dB}$ frequency, $f_{H}$ .

Question 8

For the amplifier circuit in Fig. 10.8.1


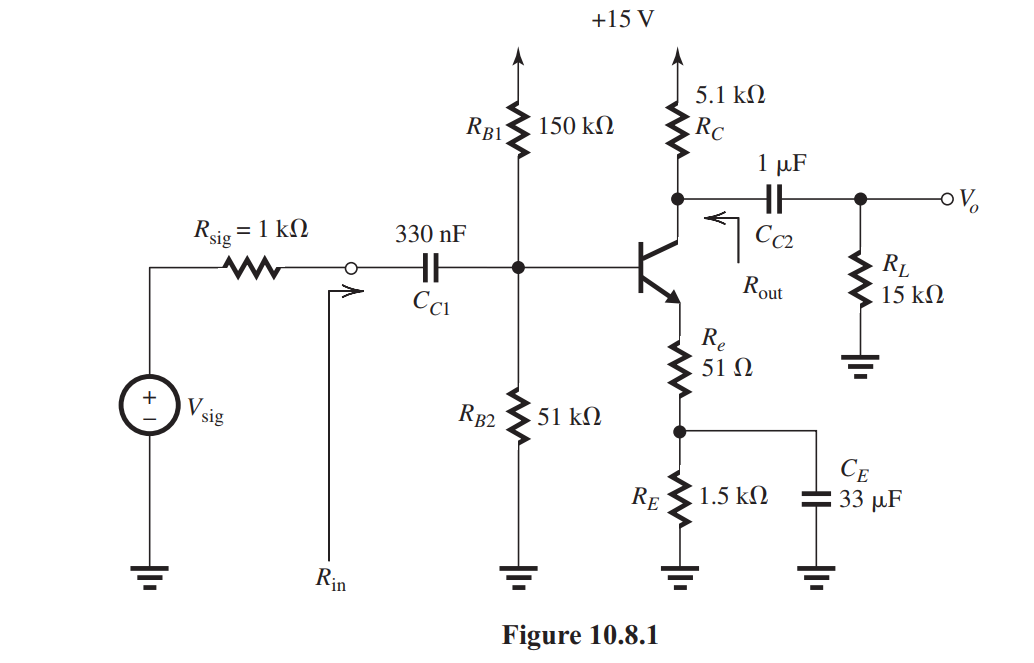
, assume that the BJT has $V_{B E}=$ $0.7 \mathrm{~V}$ and $\beta=100$ and neglect the Early effect.
(a) Find the dc bias current $I_{C}$ and the de collector voltage $V_{C}$ .
(b) Give the small-signal equivalent circuit together with values of all its components, utilizing the T model for the BJT.
(c) Find the input resistance $R_{\text {in }}$ .
(d) Find output resistance $R_{\text {out }}$ .
(e) Find the overall midband gain $V_{o} / V_{\text {sig. }}$ .
(f) Use the method of short-circuit time constants to obtain an estimate of the 3-dB frequency $f_{L}$ .

Question 9

The MOSFET in the common-source amplifier in Fig. 10.9.1


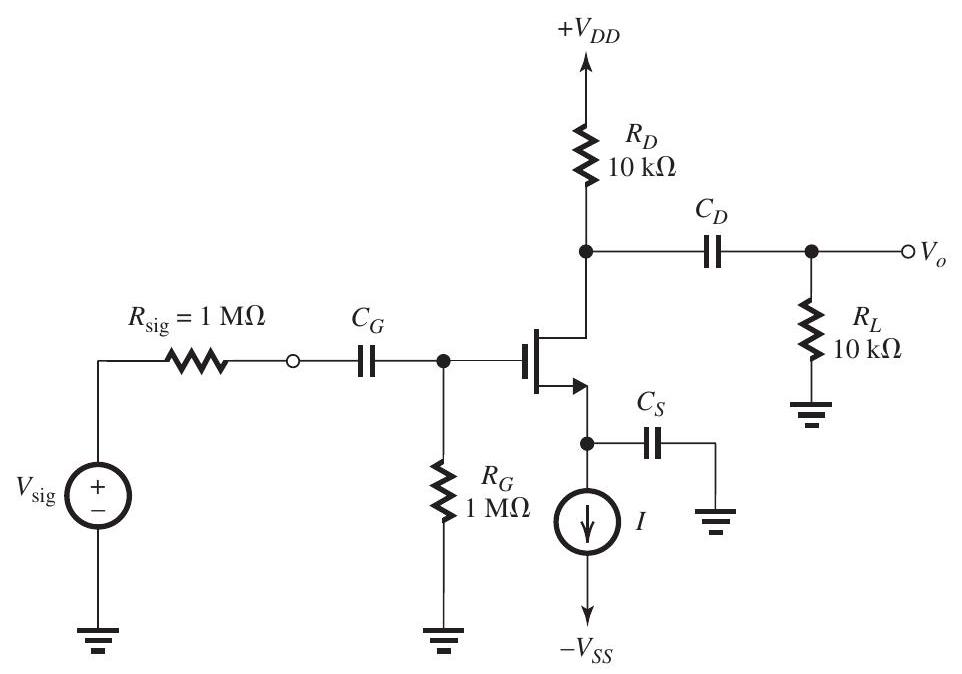
Figure 10.9.1
is operating at $g_{m}=5 \mathrm{~mA} / \mathrm{V}$ and has $C_{g s}=1 \mathrm{pF}$ and $C_{g d}=0.2 \mathrm{pF}$ . Channel-length modulation is negligibly small.
(a) Find the midband voltge gain in $\mathrm{dB}$ .
(b) Find the upper 3-dB frequency, $f_{H}$ .
(c) Find the value of $C_{G}$ that places the pole it introduces at $1 \mathrm{~Hz}$ .
(d) Find the value of $C_{S}$ that places the pole it introduces at $100 \mathrm{~Hz}$
(e) Find the value of $C_{D}$ that places the pole it introduces at $10 \mathrm{~Hz}$ .
(f) Sketch and carefully label the Bode plot for the gain magnitude. Specify the lower 3-dB frequency, $f_{L}$ .

Question 10

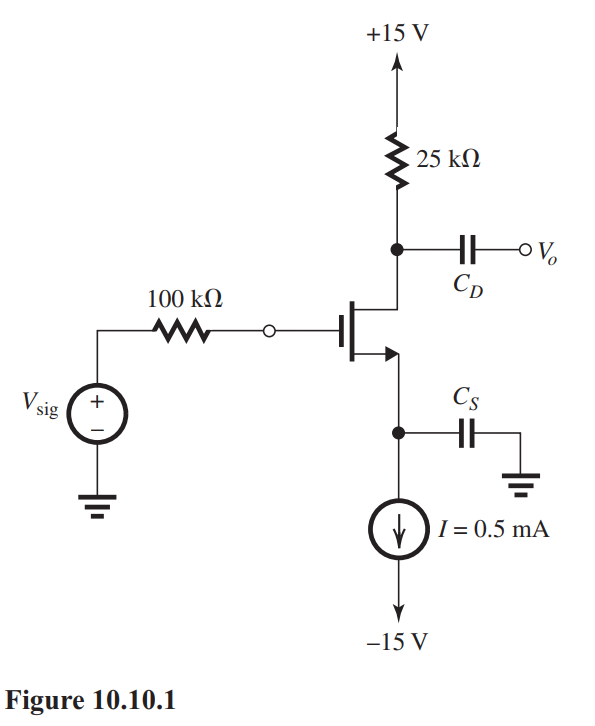
In the common-source amplifier shown in Fig. 10.10.1, the signal source has a zero average and provides de continuity to ground. The MOSFET has $V_{t}=1 \mathrm{~V}$ and $k_{n}=16 \mathrm{~mA} / \mathrm{V}^{2}$ .
(a) Find the value of $g_{m}$ at which the device is operating.
(b) Find the midband gain $V_{o} / V_{\text {sig }}$ in $\mathrm{V} / \mathrm{V}$ and in dB.
(c) Find the value of $C_{S}$ that places the lower 3-dB frequency $\omega_{L}$ at $100 \mathrm{rad} / \mathrm{s}$ .
(d) If $C_{g s}=1 \mathrm{pF}$ and $C_{g d}=0.2 \mathrm{pF}$ , find the value of the upper $3-\mathrm{dB}$ frequency, $\omega_{H}$ .
(e) It is desired to double $\omega_{H}$ by changing the value of $g_{m}$ (through changing the bias current $I$ ), find the required value of $I$ , the new value of the midband gain (in $\mathrm{V} / \mathrm{V}$ and in $\mathrm{dB}$ ), and the new value of $\omega_{L}$ .