Deck 13: Recursion
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/50
Play
Full screen (f)
Deck 13: Recursion
1
One reason modular programming is encouraged is that it is an efficient way to manage computer memory.
True
2
Because variables declared in a module are local, and arguments passed by value are copied into local variables, a module can run like an independent program.
True
3
Variables declared in a module are also available to other modules.
False
4
The factorial of a number is the product of all positive integers from that number down to 1.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
5
Any recursive procedure can be described nonrecursively.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
6
The following algorithm defines a nonrecursive Fibonacci function:
Function Numeric factorial(Numeric num)
// Declare variables
Declare Numeric fact = 1 // factorial result
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
fact = fact * index
End For
Return fact
End Function
Function Numeric factorial(Numeric num)
// Declare variables
Declare Numeric fact = 1 // factorial result
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
fact = fact * index
End For
Return fact
End Function

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
7
The factorial of 4 is the same as 4 times the factorial of 3.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
8
The factorial of 3 is the same as 2 times the factorial of 2.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
9
The factorial of 7 is 504.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
10
The factorial of 6 is 720.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
11
A factorial can be defined as factorial(n) = n * factorial(n - 1), with factorial(1) defined as 1.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
12
The Fibonacci number at any position (after the first two numbers in the sequence) is the sum of the Fibonacci number at two positions before the current one and the Fibonacci number at one position before the current one.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
13
For any integer n greater than or equal to 2, you can represent its position in the Fibonacci sequence, starting the position numbering at 0, as follows:
fibonacci(n) = fibonacci(n - 2) + fibonacci(n - 1)
fibonacci(n) = fibonacci(n - 2) + fibonacci(n - 1)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
14
The Fibonacci sequence was mentioned in the 2006 movie The DaVinci Code.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
15
For any positive number n, the sum of squares equals 1<sup>2</sup> + 2<sup>2</sup> + 3<sup>2</sup>, and so on up to n<sup>2</sup>.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
16
The sum of squares of 3 and 5 is 24.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
17
The sum of squares of -3 and -8 is 72.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
18
Legend says that when the Towers of Hanoi puzzle is completed, the world will come to an end.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
19
The Towers of Hanoi puzzle is attributed to the French mathematician Edouard Lucas and is based on a legend about a temple in Vietnam, with 64 golden discs stacked on three posts.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
20
The Towers of Hanoi puzzle can be solved with recursion.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
21
The greatest common denominator (GCD) of two numbers is the largest integer that can be divided by both numbers evenly (with no remainder).

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
22
The mathematician Euclid discovered a method for computing the GCD.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
23
The greatest common denominator of 79 and 51 is 3.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
24
The greatest common denominator of 62 and 22 is 1.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
25
Constructor functions cannot be called recursively.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
26
____ is a process in which a module calls itself.
A) Stack overflow
B) Short-circuit evaluation
C) Recursion
D) Garbage collection
A) Stack overflow
B) Short-circuit evaluation
C) Recursion
D) Garbage collection

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
27
To prevent a neverending recursion process, you must make sure to build a(n) ____ into the procedure.
A) base case
B) sentinel
C) index
D) constructor
A) base case
B) sentinel
C) index
D) constructor

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
28
A(n) ____ is an event that does not call itself and must be reached eventually.
A) base case
B) sentinel
C) index
D) constructor
A) base case
B) sentinel
C) index
D) constructor

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
29
A program's main module occupies a designated place in memory called the ____.
A) branch
B) stub
C) stack
D) base
A) branch
B) stub
C) stack
D) base

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
30
A memory stack contains the main program, and when another module is running, it is said to be placed, or ____ the memory stack until it is finished executing.
A) deposited onto
B) pushed onto
C) withdrawn from
D) popped from
A) deposited onto
B) pushed onto
C) withdrawn from
D) popped from

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
31
____ occurs if a recursive procedure contains no base case.
A) Field testing
B) Housekeeping
C) Stack overflow
D) Data hiding
A) Field testing
B) Housekeeping
C) Stack overflow
D) Data hiding

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
32
5! * 5! is ____.
A) 120
B) 720
C) 5040
D) 14400
A) 120
B) 720
C) 5040
D) 14400

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
33
6! / (2! * 4!) = ____.
A) 2
B) 15
C) 24
D) 32
A) 2
B) 15
C) 24
D) 32

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
34
4!/0! = ____.
A) 2
B) 15
C) 24
D) 32
A) 2
B) 15
C) 24
D) 32

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
35
(10! / 5!) / 10 = ____.
A) 720
B) 1440
C) 3024
D) 5040
A) 720
B) 1440
C) 3024
D) 5040

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following represents the factorial function?
A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function
B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function
C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function
D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module
A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function
B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function
C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function
D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
37
The following sequence is known as the ____.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...
A) sum of squares
B) Towers of Hanoi
C) Fibonacci sequence
D) factorial sequence
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...
A) sum of squares
B) Towers of Hanoi
C) Fibonacci sequence
D) factorial sequence

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
38
Which of the following represents the Fibonnacci sequence?
A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function
B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function
C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1 // factorial result
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function
D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module
A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function
B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function
C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1 // factorial result
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function
D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following represents the sum of squares?
A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function
B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function
C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function
D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module
A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function
B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function
C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function
D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
40
The sum of squares of -5 and -7 is ____.
A) 28
B) 74
C) 82
D) 94
A) 28
B) 74
C) 82
D) 94

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
41
The sum of squares of the first two even integers is ____.
A) 5
B) 10
C) 15
D) 20
A) 5
B) 10
C) 15
D) 20

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
42
The sum of squares can be defined as ____.
A) (num) + sumOfSquares(num - 1)
B) (num / num) + sumOfSquares(num - 1)
C) (num * num) + sumOfSquares(num - 1)
D) (num * num) + sumOfSquares(num)
A) (num) + sumOfSquares(num - 1)
B) (num / num) + sumOfSquares(num - 1)
C) (num * num) + sumOfSquares(num - 1)
D) (num * num) + sumOfSquares(num)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
43
Which of the following is played with three pegs and a stack of discs?
A) The Towers of Hanoi
B) Chess
C) The sum of squares
D) Checkers
A) The Towers of Hanoi
B) Chess
C) The sum of squares
D) Checkers

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
44
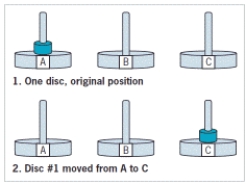
-The accompanying figure represents the ____.
A) Towers of Hanoi
B) Fibonacci sequence
C) sum of squares
D) factorial sequence

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
45
Which of the following represents the Towers of Hanoi?
A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function
B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function
C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function
D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module
A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function
B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function
C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function
D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
46
What is the greatest common denominator of 30 and 36?
A) 1
B) 2
C) 4
D) 6
A) 1
B) 2
C) 4
D) 6

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
47
What is the greatest common denominator of 87 and 41?
A) 1
B) 2
C) 4
D) 6
A) 1
B) 2
C) 4
D) 6

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
48
What is the greatest common denominator of 36 and 22?
A) 1
B) 2
C) 4
D) 6
A) 1
B) 2
C) 4
D) 6

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
49
What is the greatest common denominator of 105 and 35?
A) 5
B) 15
C) 25
D) 35
A) 5
B) 15
C) 25
D) 35

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
50
The following algorithm represents the ____.
Function Numeric unKnown(Numeric x, Numeric y)
If y = 0 Then
Return x
Else
Return GCD(y, x % y)
End If
End Function
A) sum of squares
B) Fibonacci series
C) GCD function
D) factorial series
Function Numeric unKnown(Numeric x, Numeric y)
If y = 0 Then
Return x
Else
Return GCD(y, x % y)
End If
End Function
A) sum of squares
B) Fibonacci series
C) GCD function
D) factorial series

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck



