Deck 2: Functions and Their Graphs
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/157
Play
Full screen (f)
Deck 2: Functions and Their Graphs
1
Suppose that f and g are the functions defined by the tables below. What is the domain of f ?
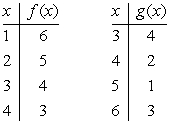
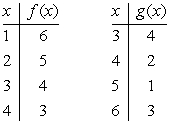
{1, 2, 3, 4}
2
Suppose that f and g are the functions defined by the tables below. What is the domain of g? 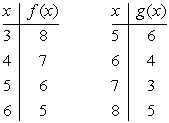
A) {3, 4, 5, 6}
B) {5, 6, 7, 8}
C) {1, 2, 3, 7}
D) {2, 3, 4, 6}
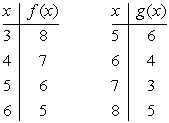
A) {3, 4, 5, 6}
B) {5, 6, 7, 8}
C) {1, 2, 3, 7}
D) {2, 3, 4, 6}
{5, 6, 7, 8}
3
Suppose that f and g are the functions defined by the tables below. What is the range of f ?
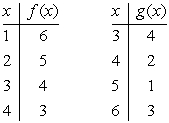
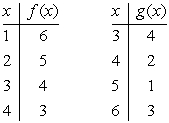
{3, 4, 5, 6}
4
Suppose that f is the function defined by the table below. The number 6 is in the domain of f.
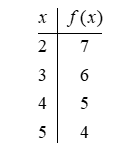
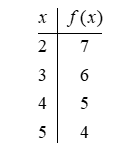

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose that f and g are the functions defined by the tables below. What is the range of g? 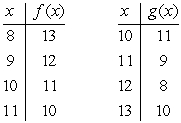
A) {8, 9, 10, 11}
B) {9, 10, 11, 12}
C) {10, 11, 12, 13}
D) {7, 8, 9, 10}
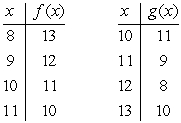
A) {8, 9, 10, 11}
B) {9, 10, 11, 12}
C) {10, 11, 12, 13}
D) {7, 8, 9, 10}

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
6
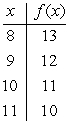
Suppose that f is the function defined by the table below. Give the table of values of f -1.


Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose that g is the function defined by the table below. The number 7 is in the domain of .



Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
8
Suppose that f is the function defined by the table below. What is the domain of f -1? 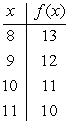
A) {8, 9, 10, 11}
B)
C) {10, 11, 12, 13}
D) {8, 10, 12, 14}

A) {8, 9, 10, 11}
B)
C) {10, 11, 12, 13}
D) {8, 10, 12, 14}

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose that g is the function defined by the table below. What is the range of g -1?



Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
10
If the function f is given by the following table, then can be represented by the adjacent graph.



Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
11
Sketch the graph of g -1, where g is the function defined by the table below.
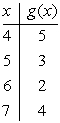
A)

B)

C)
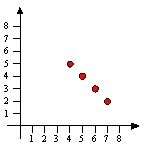
D)
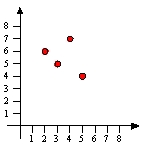

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
12
If f is defined by the first table of values, then is defined for the last table of values, regardless the value of k.
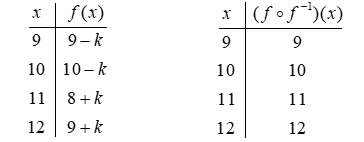
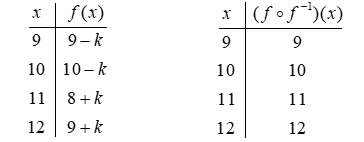

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose that f and g are the functions defined by the tables below. Give the table of values of
.
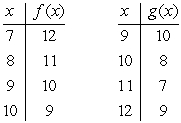
.
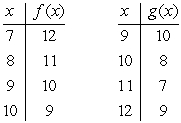

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose that f and g are the functions defined by the tables below. Give the table of values of
.
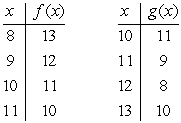
.
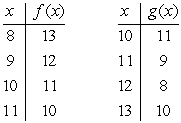

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
15
Consider the function f with domain [0, 12] whose graph is shown below.
![<strong>Consider the function f with domain [0, 12] whose graph is shown below. </strong> A) What is the largest interval contained in the domain of f on which f is increasing? B) Let g denote the function obtained from f by restricting the domain to the interval in part (a). What is the domain of g <sup>-</sup><sup>1</sup> ?](https://d2lvgg3v3hfg70.cloudfront.net/TB10659/11eec3ef_33d2_d8c5_ae1f_11e0d78d41d2_TB10659_00.jpg)
A) What is the largest interval contained in the domain of f on which f is increasing?
B) Let g denote the function obtained from f by restricting the domain to the interval in part (a). What is the domain of g -1 ?
![<strong>Consider the function f with domain [0, 12] whose graph is shown below. </strong> A) What is the largest interval contained in the domain of f on which f is increasing? B) Let g denote the function obtained from f by restricting the domain to the interval in part (a). What is the domain of g <sup>-</sup><sup>1</sup> ?](https://d2lvgg3v3hfg70.cloudfront.net/TB10659/11eec3ef_33d2_d8c5_ae1f_11e0d78d41d2_TB10659_00.jpg)
A) What is the largest interval contained in the domain of f on which f is increasing?
B) Let g denote the function obtained from f by restricting the domain to the interval in part (a). What is the domain of g -1 ?

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the function f with domain [0, 12] whose graph is shown below.
![<strong>Consider the function f with domain [0, 12] whose graph is shown below. </strong> A) What is the largest interval contained in the domain of f on which f is decreasing? B) Let h denote the function obtained from f by restricting the domain to the interval in part (a). What is the range of h <sup>-</sup><sup>1</sup> ?](https://d2lvgg3v3hfg70.cloudfront.net/TB10659/11eec3ef_33d2_d8c6_ae1f_cfd86952b47e_TB10659_00.jpg)
A) What is the largest interval contained in the domain of f on which f is decreasing?
B) Let h denote the function obtained from f by restricting the domain to the interval in part (a). What is the range of h -1 ?
![<strong>Consider the function f with domain [0, 12] whose graph is shown below. </strong> A) What is the largest interval contained in the domain of f on which f is decreasing? B) Let h denote the function obtained from f by restricting the domain to the interval in part (a). What is the range of h <sup>-</sup><sup>1</sup> ?](https://d2lvgg3v3hfg70.cloudfront.net/TB10659/11eec3ef_33d2_d8c6_ae1f_cfd86952b47e_TB10659_00.jpg)
A) What is the largest interval contained in the domain of f on which f is decreasing?
B) Let h denote the function obtained from f by restricting the domain to the interval in part (a). What is the range of h -1 ?

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the function f with domain (0, 20] whose graph is shown below, where a = 4, b = 12, and c = 20. Find the largest interval where f is increasing.
![<strong>Consider the function f with domain (0, 20] whose graph is shown below, where a = 4, b = 12, and c = 20. Find the largest interval where f is increasing. </strong> A) (0, 4] B) (12, 20) C) [8, 20] D) [12, 20]](https://d2lvgg3v3hfg70.cloudfront.net/TB10659/11eec3ef_33d2_d8c7_ae1f_4b6bd66fecd5_TB10659_00.jpg)
A) (0, 4]
B) (12, 20)
C) [8, 20]
D) [12, 20]
![<strong>Consider the function f with domain (0, 20] whose graph is shown below, where a = 4, b = 12, and c = 20. Find the largest interval where f is increasing. </strong> A) (0, 4] B) (12, 20) C) [8, 20] D) [12, 20]](https://d2lvgg3v3hfg70.cloudfront.net/TB10659/11eec3ef_33d2_d8c7_ae1f_4b6bd66fecd5_TB10659_00.jpg)
A) (0, 4]
B) (12, 20)
C) [8, 20]
D) [12, 20]

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the function f whose graph is shown below. Find the interval(s) where the function is decreasing. Here, a = -8, b = -4, c = 6, and d = 20.
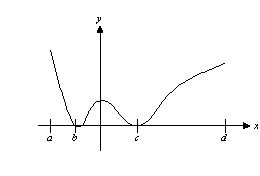


Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
19
Every odd function is one-to-one.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
20
The sum of two decreasing functions is decreasing.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the function f whose graph is shown below. Use the horizontal line test to determine if the function has an inverse.
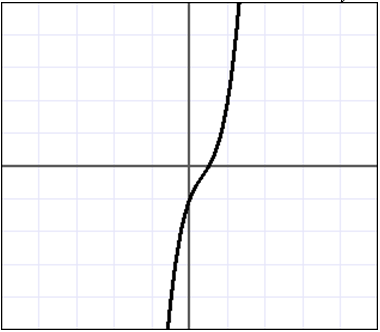


Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the function f whose graph is shown below. Sketch the graph of the inverse.



Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose f(x) = 9x + 1. Evaluate f -1(10).

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
24
Suppose f(x) = -x - 16. Evaluate f -1(-11).
A) 16
B) 14
C) -5
D) 15
A) 16
B) 14
C) -5
D) 15

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
25
Suppose . Evaluate f -1(2).

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose
. Evaluate f -1(14).
. Evaluate f -1(14).

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
27
Suppose f(x) = 43x + 1. Find a formula for f -1.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
28
Suppose f(x) = 2x + 7. Find a formula for f -1.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose . Evaluate f -1(4).
A) 4
B) 5
C) 3
D) -4
A) 4
B) 5
C) 3
D) -4

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose . Evaluate f -1(-11).

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
31
Suppose h(x) = -11 + x2, where the domain of h is the set of positive numbers. Find a formula for h-1.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
32
Suppose h(x) = -6 - 2x2, where the domain of h is the set of positive numbers. Find a formula for h-1.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
33
Suppose . Find the domain of f.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
34
Suppose . Find the domain of f -1.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose . Find the range of f -1.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
36
Suppose . Find the range of f.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
37
Suppose f(x) = x2 + 20, where the domain of f equals
. Find the range of f.
. Find the range of f.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose f(x) = 2 - 16x2, where the domain of f equals . Find the domain of f -1.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose f(x) = x5 + 17x3. Which of the following alternatives equals ?
A) 1
B)
C)
D)
A) 1
B)
C)
D)

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose f(x) = 5x3 + x. Which of the following alternatives equals f -1(630)?
A) 5
B)
C) 6
D)
A) 5
B)
C) 6
D)

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
41
Suppose f(x) = x7 + x5. Evaluate (f -1(13))7 + (f -1(13))5 + 13.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
42
Suppose f(x) = x7 + 2x3. Evaluate (f -1(12))7 + 2(f -1(12))3 + 1.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
43
Suppose and . Evaluate .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
44
Suppose and . Evaluate .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose And . Then which must be true?
A)
B)
C)
D) Impossible to determine
A)
B)
C)
D) Impossible to determine

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
46
Suppose and . Determine if f and g are inverses.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
47
Suppose and . Determine if f and g are inverses.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose on the domain Determine if f has an inverse.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
49
Assuming that f and g are the functions completely defined by the tables below, evaluate the expression
.
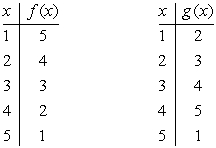
.


Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
50
Assuming that g is the function completely defined by the table below, evaluate the expression .



Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
51
Assuming that f and g are the functions completely defined by the tables below, evaluate the expression
.
.


Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
52
Assuming that f is the function completely defined by the table below, evaluate the expression .

A) 2
B) 1
C) 0
D) 3

A) 2
B) 1
C) 0
D) 3

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate assuming that and .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate assuming that and .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
55
Evaluate Assuming that And .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
56
Evaluate assuming that and .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
57
Suppose . If f(x) = (x + 9)2, then find a function g such that .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
58
Suppose . If , then find a function g such that .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
59
Suppose . If , then find a function f such that .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
60
Suppose . If , then find a function f such that .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
61
Suppose . If , then find a function f such that .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
62
For And , find a formula for . Simplify your results as much as possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
63
For and , find a formula for . Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
64
For and , find a formula for . Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
65
if then f(g(x)) = g(f(x)) for each x > 0.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
66
Find a number b such that , where and .

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
67
Find a number c such that , where .
A) 241
B) -239
C) -209
D) -210
A) 241
B) -239
C) -209
D) -210

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
68
If f(x) = 6x + b and g(x) = 6x + c, then f g = g f if and only if b = c.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
69
For and , find a formula for . Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
70
For and , find a formula for . Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
71
For and , find a formula for
. Simplify your results as much as possible.
. Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
72
For and , find a formula for . Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
73
For and , find a formula for . Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
74
For and , find a formula for . Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
75
For and , find a formula . Simplify your results as much as possible.

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
76
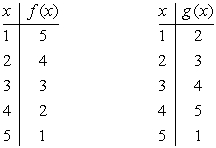
Choose the composite of functions that would create the graph: 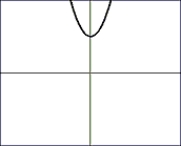
A) For And
B) For And
C) For And
D) For And

A) For And
B) For And
C) For And
D) For And

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
77
Choose the composite of functions that would create the graph:

A) For And
B) For And
C) For And
D) For And

A) For And
B) For And
C) For And
D) For And

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
78
Choose the composite of functions that would create the graph:
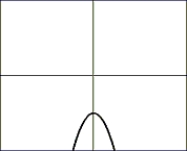
A) For And
B) For And
C) For And
D) For And

A) For And
B) For And
C) For And
D) For And

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
79
Choose the composite of functions that would create the graph:

A) For And
B) For And
C) For And
D) For And

A) For And
B) For And
C) For And
D) For And

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck
80
Choose the composite of functions that would create the graph:
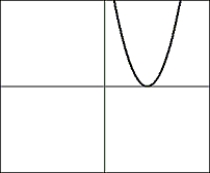
A) For And
B) For And
C) For And
D) For And

A) For And
B) For And
C) For And
D) For And

Unlock Deck
Unlock for access to all 157 flashcards in this deck.
Unlock Deck
k this deck



