Deck 4: Transmission Lines: Steady-State Operation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/14
Play
Full screen (f)
Deck 4: Transmission Lines: Steady-State Operation
1
A three-phase line has a positive-sequence series impedance . The load at the receiving end absorbs 10 MVA at . Assuming a short line, calculate: (a) the parameters, (b) the sending-end voltage for a load power factor of 0.9 lagging, (c) the sending-end voltage for a load power factor of 0.9 leading.
(a)
(b)
(c)
(b)
(c)
2
A three-phase line has a positive-sequence series impedance and a positive-sequence shunt admittance . At full load, the line delivers at 0.99 p.f. lagging and at . Using the nominal circuit, calculate: (a) the parameters, (b) the sending-end voltage and current, and (c) the percent voltage regulation.
(b)
(c)
3
Rework Test Bank Problem 5.2 in per-unit using 100-MVA (three-phase) and 230-kV(line-to-line) base values. Calculate (a) the per-unitABCDparameters, (b) the per-unitsending-end voltage and current, and (c) the percent voltage regulation.
(a)
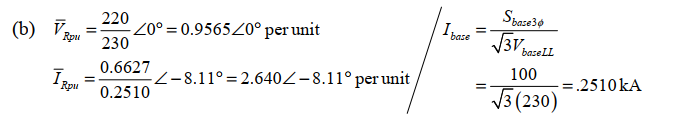
(c)
4
\underline{\underline{0.6507}
-Evaluate and for per unit.
-Evaluate and for per unit.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
5
A uncompensated three-phase line has a positive-sequence series impedance and a positive-sequence shunt admittance . Calculate: (a) , (b) , and (c) the exact parameters for this line.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
6
At full load the line in Test Bank Problem 5.5 delivers 1000 MW at unity power factor and at 480 kV. Calculate (a) thesending-end voltage, (b) the sending-end current, (c) the sending-end power factor, (d) the full-loadline losses, and (e) the percent voltage regulation.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
7
etermine the equivalent π circuit for the line in TestBank Problem 5.5 and compare it with the nominal π circuit.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
8
A three-phase uncompensated line has a positive-sequence series reactance and a positive-sequence shunt admittance . Neglecting losses, calculate: (a) , (b) , (c) the parameters, (d) the wavelength of the line, in kilometers, and (e) the surge impedance loading in MW.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
9
Determine the equivalent π circuit for the line in Test Bank Problem 5.8.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
10
Rated line voltage is appliedto the sending end of the line in Test Bank Problem 5.8.Calculate the receiving-end voltage when thereceiving end is terminated by (a) an open circuit, (b) the surge impedance of the line,and (c) one-half of thesurge impedance. (d)Also calculate the theoretical maximum realpower that the line can deliver when rated voltage is applied toboth ends of the line.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
11
The line in Test Bank Problem 5.5 has three ACSR 1113-kcmil conductors per chase.Calculate the theoretical maximum real power that this line can deliver and compare withthe thermal limit of the line. Assume VS-VR=1.0 per unit and unity power factor at thereceiving end.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
12
Repeat Test Bank Problems 5.5 and 5.11 if the line length is (a) and (b) .

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
13
For the line in Test Bank Problems 5.5 and 5.11 , determine (a) the practical line loadability in MW, assuming per unit, per unit, and ; (b) the full-load current at 0.99 leading power factor, based on the above practical line loadability; (c) the exact receiving-end voltage for the full-load current in (b) above; and (d) the percent voltage regulation. For this line, is loadability determined by the thermal limit, the drop limit, or stead-state stability?

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
14
Determine the practical line loadability in MWand in per unit of SIL for the line in Test Bank Problem 5.5 if the length is(a) 200 km and (b) 600 km. Assume VS = 1.0 per unit, VR =0.95 per unit , and 0.99 leading power factor at the receiving end.

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck



