Deck 12: Regression Analysis II Multiple Linear Regression and Other Topics
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/5
Play
Full screen (f)
Deck 12: Regression Analysis II Multiple Linear Regression and Other Topics
1
Find a linearizing transformation of y=1/(a + b x)
y' = 1/y, x' = x
2
Consider the data set

A) Obtain the best fitting straight line with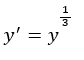
B) What proportion of the y'variability is explained by the fitted line?
Round your answers to three decimal places.

A) Obtain the best fitting straight line with
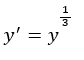
B) What proportion of the y'variability is explained by the fitted line?
Round your answers to three decimal places.
Part A: 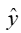 = .180 - 1.940x
= .180 - 1.940x
Part B: .993
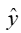 = .180 - 1.940x
= .180 - 1.940xPart B: .993
3
Suppose the price, y, per ton of copper can be modeled by  where the two predictor variables x1 and x2 are the prices per ton of zinc and lead, respectively. The least squares estimates are:
where the two predictor variables x1 and x2 are the prices per ton of zinc and lead, respectively. The least squares estimates are: 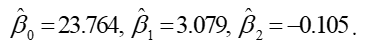
Predict the response for x1= 2389 and x2 = 2366.
 where the two predictor variables x1 and x2 are the prices per ton of zinc and lead, respectively. The least squares estimates are:
where the two predictor variables x1 and x2 are the prices per ton of zinc and lead, respectively. The least squares estimates are: 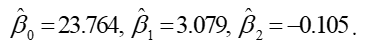
Predict the response for x1= 2389 and x2 = 2366.
$7131.07
4
Consider the multiple linear regression model
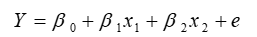
where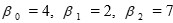 , and the normal random variable e has standard deviation 6. What is the mean of the response Y when x1 = 1 and x2 = 4?
, and the normal random variable e has standard deviation 6. What is the mean of the response Y when x1 = 1 and x2 = 4?
A) 34
B) 19
C) 40
D) 25
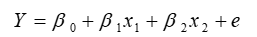
where
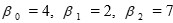 , and the normal random variable e has standard deviation 6. What is the mean of the response Y when x1 = 1 and x2 = 4?
, and the normal random variable e has standard deviation 6. What is the mean of the response Y when x1 = 1 and x2 = 4?A) 34
B) 19
C) 40
D) 25

Unlock Deck
Unlock for access to all 5 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose the price, y, per ton of copper can be modeled by 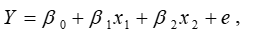
where the two predictor variables x1 and x2 are the prices per ton of zinc and lead, respectively. The least squares estimates, based on monthly observations in a five-year period, are: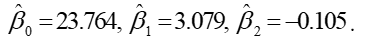
Assuming that the residual sum of squares (SSE) is 1424.48 and the SS due to regression is 5150.68.
A) Estimate the error standard deviation.
B) State the degrees of freedom used in part A.
C) Find R2.
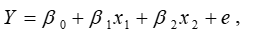
where the two predictor variables x1 and x2 are the prices per ton of zinc and lead, respectively. The least squares estimates, based on monthly observations in a five-year period, are:
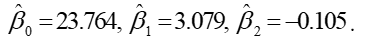
Assuming that the residual sum of squares (SSE) is 1424.48 and the SS due to regression is 5150.68.
A) Estimate the error standard deviation.
B) State the degrees of freedom used in part A.
C) Find R2.

Unlock Deck
Unlock for access to all 5 flashcards in this deck.
Unlock Deck
k this deck



