Deck 4: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/54
Play
Full screen (f)
Deck 4: Probability
1
For each numerical value assigned to the probability of an event, identify the verbal statements that are appropriate.
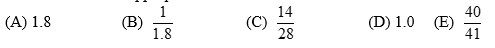 Verbal statements: (i) cannot be a probability, (ii) the event is very unlikely to happen, (iii) 50-50 chance of happening, (iv) sure to happen, (v) more likely to happen that not.
Verbal statements: (i) cannot be a probability, (ii) the event is very unlikely to happen, (iii) 50-50 chance of happening, (iv) sure to happen, (v) more likely to happen that not.
Write your answer using the Roman numeral, that is, i, ii, iii, iv or v.
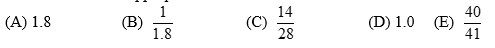 Verbal statements: (i) cannot be a probability, (ii) the event is very unlikely to happen, (iii) 50-50 chance of happening, (iv) sure to happen, (v) more likely to happen that not.
Verbal statements: (i) cannot be a probability, (ii) the event is very unlikely to happen, (iii) 50-50 chance of happening, (iv) sure to happen, (v) more likely to happen that not.Write your answer using the Roman numeral, that is, i, ii, iii, iv or v.
Part A: i
Part B: v
Part C: iii
Part D: iv
Part E: v
Part B: v
Part C: iii
Part D: iv
Part E: v
2
Construct a sample space for the following experiment.
From an urn with six balls labeled 1 through 6, five balls are chosen simultaneously. If an elementary outcome is given by the balls 2 and 5, denote it by 25, writing the numbers in ascending order.
From an urn with six balls labeled 1 through 6, five balls are chosen simultaneously. If an elementary outcome is given by the balls 2 and 5, denote it by 25, writing the numbers in ascending order.
{12345, 12346, 12356, 12456, 13456, 23456}
3
There are five elementary outcomes in a sample space. If P(e1) = 0.13, P(e2) = 0.06,
P(e3) = 0.16, and P(e4) = 0.1, what is the probability of e5?
P(e3) = 0.16, and P(e4) = 0.1, what is the probability of e5?
0.55
4
Suppose S= {e1, e2, …., e4}. If the simple events e1, e2, …., e4 are all equally likely, what are the numerical values of P(e1), P(e2), …., P(e4)? Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose S= {e1, e2 e3} . If P(e1) = 0.4 and P (e3)= 0.5 what is the probability of e2?
A) 0.1
B) 0.9
C) -0.4
D) 1
A) 0.1
B) 0.9
C) -0.4
D) 1

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
6
The sample space of an experiment is S= {e1, e2 e3} . Is the following assignment of probabilities permissible?
P(e1)=0.2 , P(e2)=0.5 , P(e3)=0.2
P(e1)=0.2 , P(e2)=0.5 , P(e3)=0.2

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
7
Express the following statement in terms of probability.
The odds are 7 to 8 that a South American team will win FIFA's World Cup.
The odds are 7 to 8 that a South American team will win FIFA's World Cup.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
8
Jackson County, Florida, has a population of 49,656, among them, 10,030 are persons under 18 years old. Estimate the probability that a person from this county, chosen at random, is under 18 years old. Round your answer two decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the experiment of tossing a coin nine times. Find the probability of getting exactly one head.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
10
A letter is chosen at random from the word "OHIO". What is the probability that it is a vowel ? Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
11
The spades and diamonds of a playing cards deck are placed in two separate piles. One card is drawn from each pile. Assume that A = 1 (ace), J = 11 (jack), Q = 12 (queen), and K = 13 (king).
Consider the following events:
A: the sum equals 8
B: the sum is odd
C: the sum is prime
D: both cards are face cards (J, Q, or K)
A) Find P(A)
B) Find P(B)
C) Find P(C)
D) Find P(D)
Round your answers to three decimal places.
Consider the following events:
A: the sum equals 8
B: the sum is odd
C: the sum is prime
D: both cards are face cards (J, Q, or K)
A) Find P(A)
B) Find P(B)
C) Find P(C)
D) Find P(D)
Round your answers to three decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
12
An experiment consists of tossing a coin, rolling a die, and tossing a coin again.
A) What is the probability of getting a head, a tail, and a number less than 5?
B) What is the probability of getting a number larger than 5?
C) What is the probability of getting at most one head?
Write your answer as a fraction reduced to lowest terms.
A) What is the probability of getting a head, a tail, and a number less than 5?
B) What is the probability of getting a number larger than 5?
C) What is the probability of getting at most one head?
Write your answer as a fraction reduced to lowest terms.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
13
A population projection for the 50 states and DC are grouped in the following frequency table.
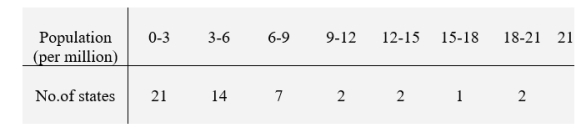 (End point convention: lower point is included, upper is not.)
(End point convention: lower point is included, upper is not.)
If one state is selected at random, what is the probability that the population prediction is:
(A) Under 9?
(B) Under 15 but not under 3?
(C) 12 or over?
Round your answers to three decimal places.
 (End point convention: lower point is included, upper is not.)
(End point convention: lower point is included, upper is not.)If one state is selected at random, what is the probability that the population prediction is:
(A) Under 9?
(B) Under 15 but not under 3?
(C) 12 or over?
Round your answers to three decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
14
Friends will be called, one after another, and asked to go on a weekend trip with you. You will call until one agrees to go (A) or four friends are asked. What is the tree diagram for the sample space for this experiment?
A)
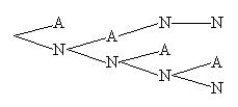
B)
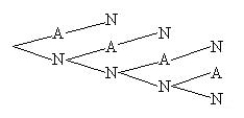
C)
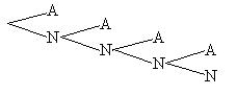
D)
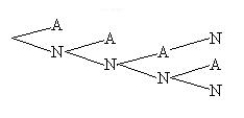
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
15
Pioneer Of The Nile (A), I Want Revenge (B), and Hold Me Back (C), were the three favorites to win the Kentucky Derby one year. According to an expert, they should arrive first, second and third, respectively.
The tree diagram for the sample space is given below.
A) Complete, the tree diagram from top to bottom
B) State the composition of the event E = [exactly two horses arrived in the predicted place]
![<strong>Pioneer Of The Nile (A), I Want Revenge (B), and Hold Me Back (C), were the three favorites to win the Kentucky Derby one year. According to an expert, they should arrive first, second and third, respectively. The tree diagram for the sample space is given below.</strong> A) Complete, the tree diagram from top to bottom B) State the composition of the event E = [exactly two horses arrived in the predicted place]](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_b019_a255_3be74429a7aa_TB10841_00.jpg)
The tree diagram for the sample space is given below.
A) Complete, the tree diagram from top to bottom
B) State the composition of the event E = [exactly two horses arrived in the predicted place]
![<strong>Pioneer Of The Nile (A), I Want Revenge (B), and Hold Me Back (C), were the three favorites to win the Kentucky Derby one year. According to an expert, they should arrive first, second and third, respectively. The tree diagram for the sample space is given below.</strong> A) Complete, the tree diagram from top to bottom B) State the composition of the event E = [exactly two horses arrived in the predicted place]](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_b019_a255_3be74429a7aa_TB10841_00.jpg)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
16
Pioneer Of The Nile (A), I Want Revenge (B), and Old Me Back (C) were the three favorites to win the Kentucky Derby one year. According to an expert, they should arrive first, second and third, respectively.
Consider the event E = [exactly two of these horses arrived in the predicted place]. Find P(E). Round your answers to two decimal places when necessary.
Consider the event E = [exactly two of these horses arrived in the predicted place]. Find P(E). Round your answers to two decimal places when necessary.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
17
The most basic event relations are: intersection, complement and ______.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
18
The sample space is given by the first 15 positive integers.
Consider the events:
A = [odd integers] B = [prime integers]
Make a Venn diagram showing these events.
A)
![<strong>The sample space is given by the first 15 positive integers. Consider the events: A = [odd integers] B = [prime integers] Make a Venn diagram showing these events.</strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_d72a_a255_33119368ac52_TB10841_00.jpg)
B)
![<strong>The sample space is given by the first 15 positive integers. Consider the events: A = [odd integers] B = [prime integers] Make a Venn diagram showing these events.</strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_d72b_a255_53f26321d405_TB10841_00.jpg)
C)
![<strong>The sample space is given by the first 15 positive integers. Consider the events: A = [odd integers] B = [prime integers] Make a Venn diagram showing these events.</strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_d72c_a255_995d5a74f17a_TB10841_00.jpg)
D)
![<strong>The sample space is given by the first 15 positive integers. Consider the events: A = [odd integers] B = [prime integers] Make a Venn diagram showing these events.</strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_d72d_a255_eff232e3ebb0_TB10841_00.jpg)
Consider the events:
A = [odd integers] B = [prime integers]
Make a Venn diagram showing these events.
A)
![<strong>The sample space is given by the first 15 positive integers. Consider the events: A = [odd integers] B = [prime integers] Make a Venn diagram showing these events.</strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_d72a_a255_33119368ac52_TB10841_00.jpg)
B)
![<strong>The sample space is given by the first 15 positive integers. Consider the events: A = [odd integers] B = [prime integers] Make a Venn diagram showing these events.</strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_d72b_a255_53f26321d405_TB10841_00.jpg)
C)
![<strong>The sample space is given by the first 15 positive integers. Consider the events: A = [odd integers] B = [prime integers] Make a Venn diagram showing these events.</strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_d72c_a255_995d5a74f17a_TB10841_00.jpg)
D)
![<strong>The sample space is given by the first 15 positive integers. Consider the events: A = [odd integers] B = [prime integers] Make a Venn diagram showing these events.</strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac4_d72d_a255_eff232e3ebb0_TB10841_00.jpg)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
19
The ______ of two events A and B, is the set of all elementary out comes that are in A and B.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
20
The intersection of A and B means that both A and B occur.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
21
Two events A and B are called ______ or mutually exclusive if their intersection empty.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
22
A sample space consists of eight elementary outcomes with the following probabilities.
P(e1) = P(e8) = 0.125, P(e2) = P(e3) = P(e4) = 0.0625, P(e5) = P(e6) = P(e7) = 0.1875.
Three events are given as
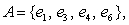
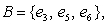
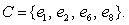 Determine the probability of:
Determine the probability of:

P(e1) = P(e8) = 0.125, P(e2) = P(e3) = P(e4) = 0.0625, P(e5) = P(e6) = P(e7) = 0.1875.
Three events are given as
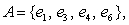
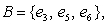
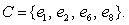 Determine the probability of:
Determine the probability of:

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
23
A sample space consists of 10 elementary outcomes e1, e2, ..., e10, whose probabilities are:
 Suppose A =
Suppose A =
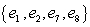 , B =
, B = 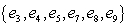 Calculate:
Calculate: 
 Suppose A =
Suppose A = 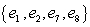 , B =
, B = 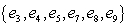 Calculate:
Calculate: 

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
24
If P(A) = 0.3 and P(B) = 0.5, can A and B be mutually exclusive?

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
25
Basic statistics on the final grades of a Biology course shown that
P(A) = 0.3 P(B) = 0.65
![Basic statistics on the final grades of a Biology course shown that P(A) = 0.3 P(B) = 0.65 where A and B are the events A = [female] B = [first time taking the course] Determinate the probabilities of:](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_2557_a255_052d5dbf48fc_TB10841_00.jpg) where A and B are the events
where A and B are the events
A = [female] B = [first time taking the course]
Determinate the probabilities of:
![Basic statistics on the final grades of a Biology course shown that P(A) = 0.3 P(B) = 0.65 where A and B are the events A = [female] B = [first time taking the course] Determinate the probabilities of:](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_4c68_a255_b171892cec97_TB10841_00.jpg)
P(A) = 0.3 P(B) = 0.65
![Basic statistics on the final grades of a Biology course shown that P(A) = 0.3 P(B) = 0.65 where A and B are the events A = [female] B = [first time taking the course] Determinate the probabilities of:](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_2557_a255_052d5dbf48fc_TB10841_00.jpg) where A and B are the events
where A and B are the eventsA = [female] B = [first time taking the course]
Determinate the probabilities of:
![Basic statistics on the final grades of a Biology course shown that P(A) = 0.3 P(B) = 0.65 where A and B are the events A = [female] B = [first time taking the course] Determinate the probabilities of:](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_4c68_a255_b171892cec97_TB10841_00.jpg)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
26
A survey taken by a journalist in a recent Climate Change Conference, shows that
P(B) = 0.7 P(S) = 0.5 P ( B S )
where B = [speak at least two languages] and S = [speak Spanish]
Find the probabilities of the following events.
A) S occurs and B does not occur.
B) Either B occurs or S does not occur.
C) Neither B nor S occur.
P(B) = 0.7 P(S) = 0.5 P ( B S )
where B = [speak at least two languages] and S = [speak Spanish]
Find the probabilities of the following events.
A) S occurs and B does not occur.
B) Either B occurs or S does not occur.
C) Neither B nor S occur.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
27
From the probabilities shown in this Venn diagram, determine the probabilities of the following events.
A) A does not occur
B) A occurs and B does not occur
C) Exactly one of the evens A and B occurs.
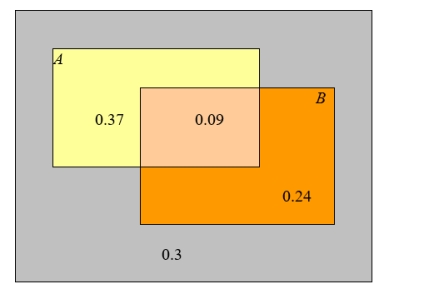
A) A does not occur
B) A occurs and B does not occur
C) Exactly one of the evens A and B occurs.


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
28
The following frequency table shows the results of 54 juniors in a state college in the science courses.
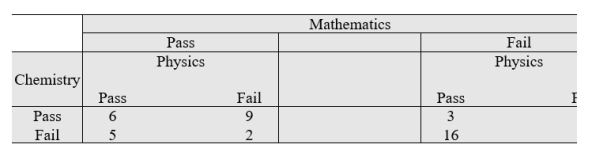 If a junior student is selected at random, find the probability that he/she has:
If a junior student is selected at random, find the probability that he/she has:
A) Passed Mathematics
B) Passed Physics and failed Chemistry and Mathematics
C) Passed any two of the three courses and failed the third
D) Passed any one of the three courses and failed the other two.
Round your answers to three decimal places.
 If a junior student is selected at random, find the probability that he/she has:
If a junior student is selected at random, find the probability that he/she has: A) Passed Mathematics
B) Passed Physics and failed Chemistry and Mathematics
C) Passed any two of the three courses and failed the third
D) Passed any one of the three courses and failed the other two.
Round your answers to three decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
29
Given two events, A and B, the revised probability of A if it is known that B has occurred is called the conditional probability of A given B.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
30
The conditional probability of B given A is defined by the formula
A)
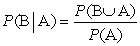
B)
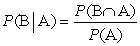
C)
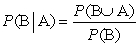
D)
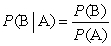
A)
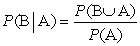
B)
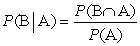
C)
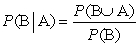
D)
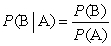

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
31
A homework assignment consists of 25 exercises. Your instructor will grade only two exercises selected at random. You have solved correctly 4 exercises. Calculate the probability that:
A) Both exercises are incorrect.
B) One exercise is incorrect and the other is correct.
Round your answers to two decimal places.
A) Both exercises are incorrect.
B) One exercise is incorrect and the other is correct.
Round your answers to two decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
32
Two events A and B are independent if:
A)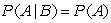
B)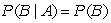
C)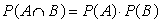
D) All of these
A)
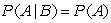
B)
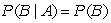
C)
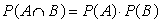
D) All of these

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
33
The following data relate to the number of cars in a parking garage.
A = Red car B = 2010 car
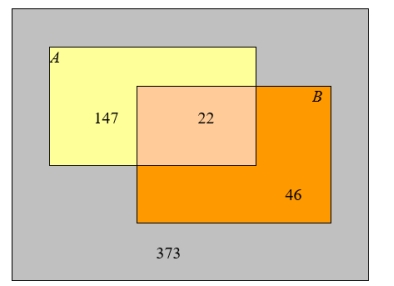
A) Find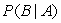 . Round your answer to three decimal places.
. Round your answer to three decimal places.
B) Are A and B independent?
A = Red car B = 2010 car

A) Find
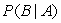 . Round your answer to three decimal places.
. Round your answer to three decimal places. B) Are A and B independent?

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
34
Suppose P(A) = 0.55, P(B) = 0.29, and  Find the conditional probability of A given that B does not occur. Round your answers to three decimal places.
Find the conditional probability of A given that B does not occur. Round your answers to three decimal places.
A) 0.634
B) 0.326
C) 0.345
D) 0.182
 Find the conditional probability of A given that B does not occur. Round your answers to three decimal places.
Find the conditional probability of A given that B does not occur. Round your answers to three decimal places.A) 0.634
B) 0.326
C) 0.345
D) 0.182

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
35
For two events A and B, the following probabilities are given.
P(A) = 0.43 P(B) = 0.27 P(A B) = 0.556
Use the appropriate laws of probabilities to calculate
A)
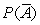
B)
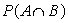
C)
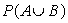
P(A) = 0.43 P(B) = 0.27 P(A B) = 0.556
Use the appropriate laws of probabilities to calculate
A)
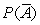
B)
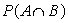
C)
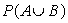

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
36
A social worker has produced the following proportions about a group of families with one children.
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_e7b9_a255_13827bd83694_TB10841_00.jpg) For a child selected at random, consider the events: A = [Live with both parents],
For a child selected at random, consider the events: A = [Live with both parents],
B = [Age between 7-12].
Find the probabilities:
A)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_e7ba_a255_3f53cd7a95b1_TB10841_00.jpg)
B)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_e7bb_a255_9f3706032b5b_TB10841_00.jpg)
C)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac6_0ecc_a255_bf06f002f942_TB10841_00.jpg)
D)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac6_0ecd_a255_65c7e7e2f531_TB10841_00.jpg)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_e7b9_a255_13827bd83694_TB10841_00.jpg) For a child selected at random, consider the events: A = [Live with both parents],
For a child selected at random, consider the events: A = [Live with both parents],B = [Age between 7-12].
Find the probabilities:
A)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_e7ba_a255_3f53cd7a95b1_TB10841_00.jpg)
B)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac5_e7bb_a255_9f3706032b5b_TB10841_00.jpg)
C)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac6_0ecc_a255_bf06f002f942_TB10841_00.jpg)
D)
![<strong>A social worker has produced the following proportions about a group of families with one children. For a child selected at random, consider the events: A = [Live with both parents], B = [Age between 7-12]. Find the probabilities: </strong> A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB10841/11ef019b_aac6_0ecd_a255_65c7e7e2f531_TB10841_00.jpg)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
37
Suppose P(A) = 0.72 and P(B) = 0.28.
A) Determine if A and B are mutually exclusive.
if A and B are mutually exclusive.
B) Determine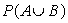 if A and B are independent.
if A and B are independent.
A) Determine
 if A and B are mutually exclusive.
if A and B are mutually exclusive. B) Determine
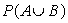 if A and B are independent.
if A and B are independent.
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
38
A state lottery has a game where you need to select one number (from 0 through 4) from each column for a total of four digits. What is the probability that your 4-digit number wins? Round your answer to five decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
39
For events A and B, the rule of total probability states:
A)
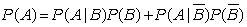
B)
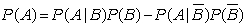
C)
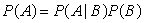
D)
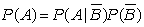
A)
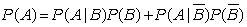
B)
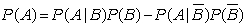
C)
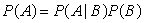
D)
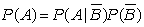

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
40
A recent study shows that 7% of North Dakota's population is left handed. If 5 persons are selected at random for an intelligence test, find P[at least one is left handed]. Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
41
An orchid nursery, specialized in Cattleya and Dendrobium types, has 200 plants, 120 are cattleyas and 32 have a bug's infection. Of the 120 cattleyas, 31 are infected.
One plant is randomly selected from the nursery. If the plant is a dendrobium, what is the probability that it is not infected?
One plant is randomly selected from the nursery. If the plant is a dendrobium, what is the probability that it is not infected?

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
42
Among the students in a Statistics course, 28% are physics majors, 38% are math majors, and 34% are biology majors. The percents of bilingual students within these three groups are 11%, 12%, and 23%, respectively.
A) What is the probability that a person selected at random from this course is bilingual?
B) What is the probability that a person selected at random from this course is a math major, knowing that is bilingual?
Round your answer to tree decimal places.
A) What is the probability that a person selected at random from this course is bilingual?
B) What is the probability that a person selected at random from this course is a math major, knowing that is bilingual?
Round your answer to tree decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
43
National Bank has two branches in the city. In the downtown office, there are 8 workers, 6 of them are female. In the uptown office, there are 15 workers, 12 of them are female. One of these 23 workers has been chosen at random for a special training. If the chosen employee is male, what is the probability that he works downtown?
Round your answers to two decimal places.
Round your answers to two decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
44
There are six well qualified applicants for two internship positions in a hospital. Three of these applicants are women and three are men. If the two interns are selected at random, what is the probability of selecting exactly two men?

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
45
Which of the following statements is true?
I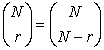
II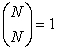
III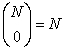
A) Only I
B) Only I and II
C) Only II and III
D) Only III
I
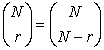
II
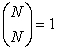
III
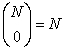
A) Only I
B) Only I and II
C) Only II and III
D) Only III

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
46
Calculate the values of:
A)
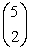
B)

C)
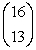
A)
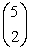
B)

C)
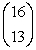

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
47
A college football team has available 5 defensive players and 3 offensive players. The coach must choose 4 players to represent the team during a Home Coming Week ceremony.
A) How many ways has the coach to select these 4 players?
B) How many selections are possible that result in 3 defensive and 1 offensive players?
C) If the players are randomly selected, what is the probability of sending to the ceremony 3 defensive and 1 offensive players? Round your answer to three decimal places.
A) How many ways has the coach to select these 4 players?
B) How many selections are possible that result in 3 defensive and 1 offensive players?
C) If the players are randomly selected, what is the probability of sending to the ceremony 3 defensive and 1 offensive players? Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
48
A sample of 10 selected from a population of 21 distinct objects is said to be a if each collection of size 10 has the same probability of being selected. What is this probability?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
49
A school bookstore sold 10 new books and 14 used books one they; one customer bought five books that day. Find the probability that:
A) Exactly three of the books bought by this customer are used.
B) At least three of the books bought by this customer are used.
C) All five of the books bought by this customer are of the same type.
A) Exactly three of the books bought by this customer are used.
B) At least three of the books bought by this customer are used.
C) All five of the books bought by this customer are of the same type.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
50
Two international flights arrived to Miami International Airport from France and Denmark. The flight from France with 31 passengers and the flight from Denmark with 27 passengers. Customs Service randomly selects five passengers for baggage inspection. What is the probability that at most three of the selected passengers have arrived in the same flight?
Round your answer to three decimal places.
Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
51
Out of 1000 students questioned, 320 only made the minimum required credit card payment at least one time in the past year.
(a) Give an estimate of the probability of
A = [ only minimum payment at least one time in a year ]
(b) Explain your reasoning.
(a) Give an estimate of the probability of
A = [ only minimum payment at least one time in a year ]
(b) Explain your reasoning.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
52
A person is randomly selected from persons working in your state. Consider the two events
A = [ Number of books read last year ] B = [ College graduate ]
(a) Given that the person is a college graduate, would you expect the probability of A to be larger, the same, or smaller than the unconditional probability P ( A )? Explain your answer.
(b) Are A and B independent according to your reasoning?
A = [ Number of books read last year ] B = [ College graduate ]
(a) Given that the person is a college graduate, would you expect the probability of A to be larger, the same, or smaller than the unconditional probability P ( A )? Explain your answer.
(b) Are A and B independent according to your reasoning?

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
53
A cable TV provider assigns 75% of its service calls to an independent contractor and 10 % of these calls result in consumer complaints. The other 25 % of the service calls are made by the companies' own employees, and these result in a 5% complaint rate.
Find the
(a) Probability of receiving a complaint.
(b) Probability that the complaint was from a customer serviced by the contractor.
Find the
(a) Probability of receiving a complaint.
(b) Probability that the complaint was from a customer serviced by the contractor.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
54
Let A be the event that a person tests positive for a virus and let B be the event that the person actually has the virus. Suppose that the virus is present in 5% of the population. Because medical tests are sometimes incorrect, we have the probabilities
.98 = P (A | B) and .022 = P (A | B )
Find
(a) the probability of a positive test
(b) the probability person has the virus given that they test positive.
.98 = P (A | B) and .022 = P (A | B )
Find
(a) the probability of a positive test
(b) the probability person has the virus given that they test positive.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck



