Deck 4: Uncertainty
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/29
Play
Full screen (f)
Deck 4: Uncertainty
1
Risk aversion is best explained by
A) timidity.
B) increasing marginal utility of income.
C) constant marginal utility of income.
D) decreasing marginal utility of income.
A) timidity.
B) increasing marginal utility of income.
C) constant marginal utility of income.
D) decreasing marginal utility of income.
D
2
Suppose a lottery ticket costs $1 and the probability that a holder will win nothing is 99.9%.What must the jackpot be for this to be a fair bet?
A) 10
B) 100
C) 1,000
D) 10,000
A) 10
B) 100
C) 1,000
D) 10,000
C
3
Expected value is defined as
A) the profit on a fair bet.
B) the most likely outcome of a given experiment.
C) the outcome that will occur on average for a given experiment.
D) the relative frequency with which an event will occur.
A) the profit on a fair bet.
B) the most likely outcome of a given experiment.
C) the outcome that will occur on average for a given experiment.
D) the relative frequency with which an event will occur.
C
4
Continuing with the same vacation-insurance company from the preceding question,what vacation-day price(s)would be acceptable to both the family and the insurance company?
A) 2 only
B) 3 only
C) 2 or 3
D) 4
A) 2 only
B) 3 only
C) 2 or 3
D) 4

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose a lottery ticket costs $1and has a jackpot of $1 million.What must the probability of winning nothing be if the bet is fair?
A) 99%
B) 99.9%
C) 99.999%
D) 99.9999%
A) 99%
B) 99.9%
C) 99.999%
D) 99.9999%

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose a lottery ticket costs $1 and the probability that a holder will win nothing is 99%.What must the jackpot be for this to be a fair bet?
A) 10
B) 100
C) 1,000
D) 10,000
A) 10
B) 100
C) 1,000
D) 10,000

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
7
People who choose not to participate in fair gambles are called
A) risk takers.
B) risk averse.
C) risk neutral.
D) broke.
A) risk takers.
B) risk averse.
C) risk neutral.
D) broke.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
8
Risk averse individuals will diversify their investments because this will
A) increase their expected returns.
B) provide them with some much-needed variety.
C) reduce the variability of their returns.
D) reduce their transactions costs.
A) increase their expected returns.
B) provide them with some much-needed variety.
C) reduce the variability of their returns.
D) reduce their transactions costs.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
9
Continuing with the same family from the preceding question,what is the greatest (integer)number of vacation days the family would be willing to give up in order to guarantee a healthy vacation?
A) 1
B) 2
C) 3
D) 4
A) 1
B) 2
C) 3
D) 4

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
10
Suppose a lottery ticket costs $1 and the probability that a holder will win nothing is 90%.What must the jackpot be for this to be a fair bet?
A) 10
B) 100
C) 1,000
D) 10,000
A) 10
B) 100
C) 1,000
D) 10,000

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
11
A gamble can be described as "fair" if the expected value of the gamble (including any costs of play)is
A) positive.
B) zero.
C) negative.
D) one.
A) positive.
B) zero.
C) negative.
D) one.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
12
Continuing with the family from the preceding question,what is their expected utility?
A)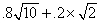
B) .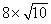
C)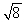
D)
A)
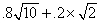
B) .
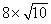
C)
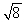
D)


Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
13
An individual will never buy complete insurance if
A) he or she is risk averse.
B) he or she is a risk taker.
C) insurance premiums are fair.
D) under any circumstances.
A) he or she is risk averse.
B) he or she is a risk taker.
C) insurance premiums are fair.
D) under any circumstances.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
14
Probability is sometimes defined as
A) the expected profit of a fair bet.
B) the most likely outcome of a given experiment.
C) the outcome that will occur on average for a given experiment.
D) the relative frequency with which an event will occur.
A) the expected profit of a fair bet.
B) the most likely outcome of a given experiment.
C) the outcome that will occur on average for a given experiment.
D) the relative frequency with which an event will occur.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
15
If a fair gamble is played many times,the combined monetary losses or gains will
A) approach zero.
B) be negative.
C) be positive.
D) result in an outcome that cannot be determined without more information.
A) approach zero.
B) be negative.
C) be positive.
D) result in an outcome that cannot be determined without more information.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
16
Continuing with the same family from the preceding question,suppose a risk neutral insurance company exists to provide vacation insurance.Suppose further that each vacation day requires a constant expenditure,and this expenditure is standard across everybody.This allows us to simplify the problem by considering all payments to be in terms of vacation days.What is the least the insurance company would charge (in terms of vacation days)?
A) 1
B) 2
C) 3
D) 4
A) 1
B) 2
C) 3
D) 4

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
17
Suppose a lottery ticket costs $1and has a jackpot of $1,000.What must the probability of winning nothing be if the bet is fair?
A) 99%
B) 99.9%
C) 99.999%
D) 99.9999%
A) 99%
B) 99.9%
C) 99.999%
D) 99.9999%

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
18
With moral hazard,fair insurance contracts are not viable because
A) individuals' aversion to risk is reduced.
B) insurance company's administrative costs are increased.
C) individuals fear unscrupulous agents.
D) probabilities of loss are increased over what is expected.
A) individuals' aversion to risk is reduced.
B) insurance company's administrative costs are increased.
C) individuals fear unscrupulous agents.
D) probabilities of loss are increased over what is expected.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
19
Continuing with the same vacation-insurance company from the preceding question,is there any vacation-day price that would both strictly increase the family's expected utility (compared to no insurance)and strictly increase the profits of the risk-neutral insurance company?
A) Yes, two days.
B) Yes, three days.
C) Yes, four days.
D) No.
A) Yes, two days.
B) Yes, three days.
C) Yes, four days.
D) No.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
20
Suppose a family has saved enough for a 10 day vacation (the only one they will be able to take for 10 years)and has a utility function U = V1/2 (where V is the number of healthy vacation days they experience).Suppose they are not a particularly healthy family and the probability that someone will have a vacation-ruining illness (V = 0)is 20%.What is the expected value of V?
A) 10
B) 8
C) 2
D) 0
A) 10
B) 8
C) 2
D) 0

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
21
Continuing with the power plant from the previous question,suppose instead the price of coal next month could be $54 or $66 (with equal probability).Now how much would it be willing to pay for an option to buy a ton of coal oil next month at today's price?
A) 5
B) 4
C) 3
D) 0
A) 5
B) 4
C) 3
D) 0

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
22
Continuing with the same family from the preceding question,what is the greatest (integer)number of vacation days the family would be willing to give up in order to guarantee a healthy vacation?
A) 3
B) 4
C) 5
D) 6
A) 3
B) 4
C) 5
D) 6

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
23
Continuing with the same vacation-insurance company from the preceding question,what vacation-day price(s)would be acceptable to both the family and the insurance company?
A) 3 or 4
B) 3, 4 or 5
C) 3, 4, 5 or 6
D) 3, 4, 5, 6 or 7
A) 3 or 4
B) 3, 4 or 5
C) 3, 4, 5 or 6
D) 3, 4, 5, 6 or 7

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
24
Continue with the power plant from the previous question,where again coal currently sells for $60 a ton but will sell for either $54 or $66 next month with equal probability.Now suppose coal can be stored for a month at the cost of $2 per ton.How would the new alternative of being able to buy coal at today's prices and store it affect the amount the power plant would be willing to pay for an option to buy coal next month at today's prices?
A) Increase its willingness to pay for the option.
B) Decrease its willingness to pay for the option.
B) Lead it to never pay for the option.
D) No effect. The new alternative of storing would never be chosen since it is worse than simply waiting and buying at next month's uncertain price.
A) Increase its willingness to pay for the option.
B) Decrease its willingness to pay for the option.
B) Lead it to never pay for the option.
D) No effect. The new alternative of storing would never be chosen since it is worse than simply waiting and buying at next month's uncertain price.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
25
Continuing with the family from the preceding question,what is their expected utility?
A)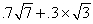
B) .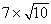
C)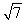
D)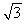
A)
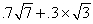
B) .
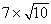
C)
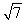
D)
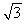

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose a family has saved enough for a 10 day vacation (the only one they will be able to take for 10 years)and has a utility function U = V1/2 (where V is the number of healthy vacation days they experience).Suppose they are not a particularly healthy family and the probability that someone will have a vacation ruining illness (V = 0)is 30%.What is the expected value of V?
A) 10
B) 7
C) 3
D) 0
A) 10
B) 7
C) 3
D) 0

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
27
Suppose a risk-neutral power plant needs 10,000 tons of coal for its operations next month.It is uncertain about the future price of coal.Today it sells for $60 a ton but next month it could be $50 or $70 (with equal probability).How much would the power plant be willing to pay today for an option to buy a ton of coal next month at today's price? (Ignore discounting over the short period of a month.)
A) 5
B) 4
C) 3
D) 0
A) 5
B) 4
C) 3
D) 0

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
28
Continuing with the same vacation-insurance company from the preceding question,is there any vacation-day price that would both strictly increase the family's expected utility (compared to no insurance)and strictly increase the profits of the risk-neutral insurance company?
A) No.
B) Yes, 3 or 4.
C) Yes, 4.
D) Yes, 4 or 5.
A) No.
B) Yes, 3 or 4.
C) Yes, 4.
D) Yes, 4 or 5.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
29
Continuing with the same family from the preceding question,suppose a risk neutral insurance company exists to provide vacation insurance.Suppose further that each vacation day requires a constant expenditure,and this expenditure is standard across everybody.This allows us to simplify the problem by considering all payments to be in terms of vacation days.What is the least the insurance company would charge (in terms of vacation days)?
A) 3
B) 4
C) 5
D) 6
A) 3
B) 4
C) 5
D) 6

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck



