Chat with AI
Deck 16: A: Auctions
Full screen (f)
Question
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 
of valuing the house at $900,000, a probability of 
of valuing it at $700,000, and a probability of 
of valuing it at $200,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $700,000
B) $800,000
C) $450,000
D) $600,000
E) $533,333.33
of valuing the house at $900,000, a probability of of valuing it at $700,000, and a probability of of valuing it at $200,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $700,000
B) $800,000
C) $450,000
D) $600,000
E) $533,333.33
Question
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $100,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $110,000, $100,000, and $25,000. The dealer believes that each bidder has a probability of 
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $89,000.
B) $100,000.
C) $105,000.
D) $80,000.
E) $78,333.33.
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $89,000.
B) $100,000.
C) $105,000.
D) $80,000.
E) $78,333.33.
Question
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $900. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $6,500, $3,600, and $900. Each bidder has a probability of 
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $5,050.
B) $3,666.67.
C) $3,600.
D) $3,100.
E) $6,500.
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $5,050.
B) $3,666.67.
C) $3,600.
D) $3,100.
E) $6,500.
Question
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $75,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $90,000, $75,000, and $30,000. The dealer believes that each bidder has a probability of 
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $75,000.
B) $69,000.
C) $60,000.
D) $82,500.
E) $65,000.
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $75,000.
B) $69,000.
C) $60,000.
D) $82,500.
E) $65,000.
Question
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $900. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $6,700, $3,400, and $900. Each bidder has a probability of 
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $5,050.
B) $3,400.
C) $2,900.
D) $3,666.67.
E) $6,700.
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $5,050.
B) $3,400.
C) $2,900.
D) $3,666.67.
E) $6,700.
Question
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $600. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $6,400, $3,000, and $600. Each bidder has a probability of 
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $2,500.
B) $4,700.
C) $3,333.33.
D) $3,000.
E) $6,400.
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $2,500.
B) $4,700.
C) $3,333.33.
D) $3,000.
E) $6,400.
Question
Question
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $85,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $100,000, $85,000, and $25,000. The dealer believes that each bidder has a probability of 
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $79,000.
B) $92,500.
C) $85,000.
D) $70,000.
E) $70,000.
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $79,000.
B) $92,500.
C) $85,000.
D) $70,000.
E) $70,000.
Question
Question
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 
of valuing the house at $900,000, a probability of 
of valuing it at $700,000, and a probability of 
of valuing it at $400,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $800,000
B) $700,000
C) $666,666.67
D) $550,000
E) $533,333.33
of valuing the house at $900,000, a probability of of valuing it at $700,000, and a probability of of valuing it at $400,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $800,000
B) $700,000
C) $666,666.67
D) $550,000
E) $533,333.33
Question
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $70,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $80,000, $70,000, and $45,000. The dealer believes that each bidder has a probability of 
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $70,000.
B) $59,000.
C) $75,000.
D) $50,000.
E) $65,000.
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $70,000.
B) $59,000.
C) $75,000.
D) $50,000.
E) $65,000.
Question
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $100. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $7,300, $2,600, and $100. Each bidder has a probability of 
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $3,333.33.
B) $2,100.
C) $2,600.
D) $4,950.
E) $7,300.
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $3,333.33.
B) $2,100.
C) $2,600.
D) $4,950.
E) $7,300.
Question
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $100,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $120,000, $100,000, and $25,000. The dealer believes that each bidder has a probability of 
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $110,000.
B) $100,000.
C) $89,000.
D) $80,000.
E) $81,666.67.
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $110,000.
B) $100,000.
C) $89,000.
D) $80,000.
E) $81,666.67.
Question
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $200. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $7,700, $3,100, and $200. Each bidder has a probability of 
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $2,600.
B) $5,400.
C) $3,666.67.
D) $3,100.
E) $7,700.
of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $2,600.
B) $5,400.
C) $3,666.67.
D) $3,100.
E) $7,700.
Question
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 
of valuing the house at $600,000, a probability of 
of valuing it at $500,000, and a probability of 
of valuing it at $200,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $500,000
B) $550,000
C) $433,333.33
D) $350,000
E) $366,666.67
of valuing the house at $600,000, a probability of of valuing it at $500,000, and a probability of of valuing it at $200,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $500,000
B) $550,000
C) $433,333.33
D) $350,000
E) $366,666.67
Question
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 
of valuing the house at $800,000, a probability of 
of valuing it at $300,000, and a probability of 
of valuing it at $100,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $300,000
B) $200,000
C) $550,000
D) $400,000
E) $366,666.67
of valuing the house at $800,000, a probability of of valuing it at $300,000, and a probability of of valuing it at $100,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $300,000
B) $200,000
C) $550,000
D) $400,000
E) $366,666.67
Question
Question
Question
Question
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 
of valuing the house at $800,000, a probability of 
of valuing it at $500,000, and a probability of 
of valuing it at $300,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $400,000
B) $533,333.33
C) $650,000
D) $500,000
E) $433,333.33
of valuing the house at $800,000, a probability of of valuing it at $500,000, and a probability of of valuing it at $300,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $400,000
B) $533,333.33
C) $650,000
D) $500,000
E) $433,333.33
Question
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 
of the cars that are auctioned are lemons and 
are good used cars. A good used car is worth $3,000 to any buyer. A lemon is worth $150 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $1,500 for cars that pass his test and $1,000 for cars that fail his test. Normal bidders will get only lemons.
B) $1,100 for cars that pass his test and $250 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,575 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get only lemons.
D) $1,000 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $300 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get good cars onlyof the time.
of the cars that are auctioned are lemons and are good used cars. A good used car is worth $3,000 to any buyer. A lemon is worth $150 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $1,500 for cars that pass his test and $1,000 for cars that fail his test. Normal bidders will get only lemons.
B) $1,100 for cars that pass his test and $250 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,575 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get only lemons.
D) $1,000 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $300 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Question
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 
of the cars that are auctioned are lemons and 
are good used cars. A good used car is worth $1,800 to any buyer. A lemon is worth $270 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $900 for cars that pass his test and $600 for cars that fail his test. Normal bidders will get only lemons.
B) $780 for cars that pass his test and $370 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,035 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get only lemons.
D) $600 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $540 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
of the cars that are auctioned are lemons and are good used cars. A good used car is worth $1,800 to any buyer. A lemon is worth $270 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $900 for cars that pass his test and $600 for cars that fail his test. Normal bidders will get only lemons.
B) $780 for cars that pass his test and $370 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,035 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get only lemons.
D) $600 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $540 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Question
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 
of the cars that are auctioned are lemons and 
are good used cars. A good used car is worth $1,200 to any buyer. A lemon is worth $270 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $735 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get only lemons.
B) $600 for cars that pass his test and $400 for cars that fail his test. Normal bidders will get only lemons.
C) $400 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
D) $580 for cars that pass his test and $370 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $540 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
of the cars that are auctioned are lemons and are good used cars. A good used car is worth $1,200 to any buyer. A lemon is worth $270 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $735 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get only lemons.
B) $600 for cars that pass his test and $400 for cars that fail his test. Normal bidders will get only lemons.
C) $400 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
D) $580 for cars that pass his test and $370 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $540 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Question
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 
of the cars that are auctioned are lemons and 
are good used cars. A good used car is worth $1,800 to any buyer. A lemon is worth $240 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $1,020 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get only lemons.
B) $900 for cars that pass his test and $600 for cars that fail his test. Normal bidders will get only lemons.
C) $760 for cars that pass his test and $340 for cars that fail his test. Normal bidders will get good cars onlyof the time.
D) $600 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $480 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
of the cars that are auctioned are lemons and are good used cars. A good used car is worth $1,800 to any buyer. A lemon is worth $240 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $1,020 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get only lemons.
B) $900 for cars that pass his test and $600 for cars that fail his test. Normal bidders will get only lemons.
C) $760 for cars that pass his test and $340 for cars that fail his test. Normal bidders will get good cars onlyof the time.
D) $600 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $480 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Question
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 
of the cars that are auctioned are lemons and 
are good used cars. A good used car is worth $2,700 to any buyer. A lemon is worth $240 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $1,470 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get only lemons.
B) $1,060 for cars that pass his test and $340 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,350 for cars that pass his test and $900 for cars that fail his test. Normal bidders will get only lemons.
D) $900 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $480 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
of the cars that are auctioned are lemons and are good used cars. A good used car is worth $2,700 to any buyer. A lemon is worth $240 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $1,470 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get only lemons.
B) $1,060 for cars that pass his test and $340 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,350 for cars that pass his test and $900 for cars that fail his test. Normal bidders will get only lemons.
D) $900 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $480 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 16: A: Auctions
1
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 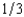of valuing the house at $900,000, a probability of 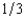of valuing it at $700,000, and a probability of 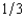of valuing it at $200,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $700,000
B) $800,000
C) $450,000
D) $600,000
E) $533,333.33
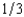of valuing the house at $900,000, a probability of 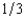of valuing it at $700,000, and a probability of 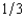of valuing it at $200,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $700,000
B) $800,000
C) $450,000
D) $600,000
E) $533,333.33
D
2
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $100,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $110,000, $100,000, and $25,000. The dealer believes that each bidder has a probability of 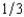of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $89,000.
B) $100,000.
C) $105,000.
D) $80,000.
E) $78,333.33.
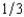of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $89,000.
B) $100,000.
C) $105,000.
D) $80,000.
E) $78,333.33.
B
3
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $900. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $6,500, $3,600, and $900. Each bidder has a probability of 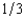of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $5,050.
B) $3,666.67.
C) $3,600.
D) $3,100.
E) $6,500.
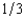of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $5,050.
B) $3,666.67.
C) $3,600.
D) $3,100.
E) $6,500.
B
4
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $75,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $90,000, $75,000, and $30,000. The dealer believes that each bidder has a probability of 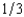of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $75,000.
B) $69,000.
C) $60,000.
D) $82,500.
E) $65,000.
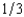of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $75,000.
B) $69,000.
C) $60,000.
D) $82,500.
E) $65,000.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $900. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $6,700, $3,400, and $900. Each bidder has a probability of 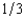of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $5,050.
B) $3,400.
C) $2,900.
D) $3,666.67.
E) $6,700.
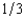of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $5,050.
B) $3,400.
C) $2,900.
D) $3,666.67.
E) $6,700.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $600. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $6,400, $3,000, and $600. Each bidder has a probability of 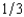of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $2,500.
B) $4,700.
C) $3,333.33.
D) $3,000.
E) $6,400.
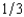of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $2,500.
B) $4,700.
C) $3,333.33.
D) $3,000.
E) $6,400.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
An antique cabinet is being sold by means of an English auction. There are four bidders, Arabella, Desiree, Gloria, and Flora. These bidders are unacquainted with each other and do not collude. Arabella values the cabinet at $1,100, Desiree values it at $600, Gloria values it at $1,700, and Flora values it at $700. If the bidders bid in their rational self-interest, the cabinet will be sold to
A) Gloria for slightly more than $1,100.
B) either Gloria or Arabella for about $1,100. Which of these two buyers gets it is randomly determined.
C) Arabella for about $1,100.
D) Gloria for about $1,700.
E) either Gloria or Arabella for about $600. Which of these two buyers gets it is randomly determined.
A) Gloria for slightly more than $1,100.
B) either Gloria or Arabella for about $1,100. Which of these two buyers gets it is randomly determined.
C) Arabella for about $1,100.
D) Gloria for about $1,700.
E) either Gloria or Arabella for about $600. Which of these two buyers gets it is randomly determined.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $85,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $100,000, $85,000, and $25,000. The dealer believes that each bidder has a probability of of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $79,000.
B) $92,500.
C) $85,000.
D) $70,000.
E) $70,000.
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $79,000.
B) $92,500.
C) $85,000.
D) $70,000.
E) $70,000.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
An antique cabinet is being sold by means of an English auction. There are four bidders, Gloria, Elise, Judy, and Arabella. These bidders are unacquainted with each other and do not collude. Gloria values the cabinet at $800, Elise values it at $500, Judy values it at $1,800, and Arabella values it at $600. If the bidders bid in their rational self-interest, the cabinet will be sold to
A) Gloria for about $800.
B) either Judy or Gloria for about $800. Which of these two buyers gets it is randomly determined.
C) Judy for slightly more than $800.
D) Judy for about $1,800.
E) either Judy or Gloria for about $500. Which of these two buyers gets it is randomly determined.
A) Gloria for about $800.
B) either Judy or Gloria for about $800. Which of these two buyers gets it is randomly determined.
C) Judy for slightly more than $800.
D) Judy for about $1,800.
E) either Judy or Gloria for about $500. Which of these two buyers gets it is randomly determined.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
10
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 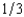of valuing the house at $900,000, a probability of 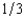of valuing it at $700,000, and a probability of 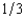of valuing it at $400,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $800,000
B) $700,000
C) $666,666.67
D) $550,000
E) $533,333.33
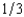of valuing the house at $900,000, a probability of 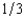of valuing it at $700,000, and a probability of 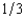of valuing it at $400,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $800,000
B) $700,000
C) $666,666.67
D) $550,000
E) $533,333.33
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $70,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $80,000, $70,000, and $45,000. The dealer believes that each bidder has a probability of 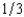of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $70,000.
B) $59,000.
C) $75,000.
D) $50,000.
E) $65,000.
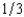of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $70,000.
B) $59,000.
C) $75,000.
D) $50,000.
E) $65,000.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $100. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $7,300, $2,600, and $100. Each bidder has a probability of 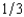of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $3,333.33.
B) $2,100.
C) $2,600.
D) $4,950.
E) $7,300.
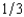of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $3,333.33.
B) $2,100.
C) $2,600.
D) $4,950.
E) $7,300.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13
A dealer decides to sell an oil painting by means of an English auction with a reservation price of slightly below $100,000. If she fails to get a bid as high as her reservation price, she will burn the painting. There are two bidders. The dealer believes that each bidder's willingness to pay will take one of the three following values: $120,000, $100,000, and $25,000. The dealer believes that each bidder has a probability of of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less than
A) $110,000.
B) $100,000.
C) $89,000.
D) $80,000.
E) $81,666.67.
of having each of these three values. The probability distribution of each buyer's value is independent of that of the other's. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the painting is slightly less thanA) $110,000.
B) $100,000.
C) $89,000.
D) $80,000.
E) $81,666.67.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
A dealer decides to sell an antique automobile by means of an English auction with a reservation price of $200. There are two bidders. The dealer believes that there are only three possible values that each bidder's willingness to pay might take, $7,700, $3,100, and $200. Each bidder has a probability of 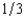of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile is
A) $2,600.
B) $5,400.
C) $3,666.67.
D) $3,100.
E) $7,700.
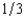of having each of these willingnesses to pay, and the probabilities of the two bidders are independent of the other's valuation. Assuming that the two bidders bid rationally and do not collude, the dealer's expected revenue from selling the automobile isA) $2,600.
B) $5,400.
C) $3,666.67.
D) $3,100.
E) $7,700.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 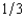of valuing the house at $600,000, a probability of 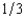of valuing it at $500,000, and a probability of 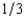of valuing it at $200,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $500,000
B) $550,000
C) $433,333.33
D) $350,000
E) $366,666.67
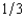of valuing the house at $600,000, a probability of 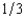of valuing it at $500,000, and a probability of 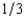of valuing it at $200,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $500,000
B) $550,000
C) $433,333.33
D) $350,000
E) $366,666.67
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. 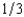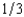First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of of valuing the house at $800,000, a probability of of valuing it at $300,000, and a probability of of valuing it at $100,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $300,000
B) $200,000
C) $550,000
D) $400,000
E) $366,666.67
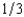of valuing the house at $800,000, a probability of of valuing it at $300,000, and a probability of 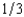of valuing it at $100,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $300,000
B) $200,000
C) $550,000
D) $400,000
E) $366,666.67
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
An antique cabinet is being sold by means of an English auction. There are four bidders, Kitty, Gloria, Judy, and Cindy. These bidders are unacquainted with each other and do not collude. Kitty values the cabinet at $800, Gloria values it at $500, Judy values it at $1,700, and Cindy values it at $700. If the bidders bid in their rational self-interest, the cabinet will be sold to
A) Judy for about $1,700.
B) Kitty for about $800.
C) either Judy or Kitty for about $800. Which of these two buyers gets it is randomly determined.
D) Judy for slightly more than $800.
E) either Judy or Kitty for about $500. Which of these two buyers gets it is randomly determined.
A) Judy for about $1,700.
B) Kitty for about $800.
C) either Judy or Kitty for about $800. Which of these two buyers gets it is randomly determined.
D) Judy for slightly more than $800.
E) either Judy or Kitty for about $500. Which of these two buyers gets it is randomly determined.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
An antique cabinet is being sold by means of an English auction. There are four bidders, Arabella, Gloria, Desiree, and Cindy. These bidders are unacquainted with each other and do not collude. Arabella values the cabinet at $1,000, Gloria values it at $800, Desiree values it at $1,300, and Cindy values it at $700. If the bidders bid in their rational self-interest, the cabinet will be sold to
A) Desiree for slightly more than $1,000.
B) Desiree for about $1,300.
C) Arabella for about $1,000.
D) either Desiree or Arabella for about $1,000. Which of these two buyers gets it is randomly determined.
E) either Desiree or Arabella for about $800. Which of these two buyers gets it is randomly determined.
A) Desiree for slightly more than $1,000.
B) Desiree for about $1,300.
C) Arabella for about $1,000.
D) either Desiree or Arabella for about $1,000. Which of these two buyers gets it is randomly determined.
E) either Desiree or Arabella for about $800. Which of these two buyers gets it is randomly determined.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19
An antique cabinet is being sold by means of an English auction. There are four bidders, Arabella, Lana, Hester, and Betsy. These bidders are unacquainted with each other and do not collude. Arabella values the cabinet at $1,000, Lana values it at $500, Hester values it at $1,300, and Betsy values it at $800. If the bidders bid in their rational self-interest, the cabinet will be sold to
A) Hester for slightly more than $1,000.
B) Hester for about $1,300.
C) Arabella for about $1,000.
D) either Hester or Arabella for about $1,000. Which of these two buyers gets it is randomly determined.
E) either Hester or Arabella for about $500. Which of these two buyers gets it is randomly determined.
A) Hester for slightly more than $1,000.
B) Hester for about $1,300.
C) Arabella for about $1,000.
D) either Hester or Arabella for about $1,000. Which of these two buyers gets it is randomly determined.
E) either Hester or Arabella for about $500. Which of these two buyers gets it is randomly determined.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20
First Fiddler's Bank has foreclosed on a home mortgage and is selling the house at auction. There are three bidders for the house, Jesse, Shelia, and Elsie. First Fiddler's does not know the willingness to pay of any of these bidders but on the basis of its previous experience believes that each of them has a probability of 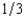of valuing the house at $800,000, a probability of 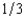of valuing it at $500,000, and a probability of 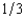of valuing it at $300,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)
A) $400,000
B) $533,333.33
C) $650,000
D) $500,000
E) $433,333.33
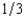of valuing the house at $800,000, a probability of 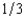of valuing it at $500,000, and a probability of 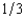of valuing it at $300,000. First Fiddler's believes that these probabilities are independent between buyers. If First Fiddler's sells the house by means of a second-bidder, sealed-bid auction (Vickrey auction), what will be the bank's expected revenue from the sale? (Choose the closest answer.)A) $400,000
B) $533,333.33
C) $650,000
D) $500,000
E) $433,333.33
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 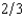of the cars that are auctioned are lemons and 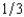are good used cars. A good used car is worth $3,000 to any buyer. A lemon is worth $150 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $1,500 for cars that pass his test and $1,000 for cars that fail his test. Normal bidders will get only lemons.
B) $1,100 for cars that pass his test and $250 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,575 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get only lemons.
D) $1,000 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $300 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get good cars onlyof the time.
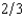of the cars that are auctioned are lemons and 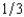are good used cars. A good used car is worth $3,000 to any buyer. A lemon is worth $150 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $1,500 for cars that pass his test and $1,000 for cars that fail his test. Normal bidders will get only lemons.
B) $1,100 for cars that pass his test and $250 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,575 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get only lemons.
D) $1,000 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $300 for cars that pass his test and $150 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
22
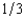Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, of the cars that are auctioned are lemons and are good used cars. A good used car is worth $1,800 to any buyer. A lemon is worth $270 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $900 for cars that pass his test and $600 for cars that fail his test. Normal bidders will get only lemons.
B) $780 for cars that pass his test and $370 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,035 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get only lemons.
D) $600 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $540 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
of the cars that are auctioned are lemons and 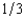are good used cars. A good used car is worth $1,800 to any buyer. A lemon is worth $270 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $900 for cars that pass his test and $600 for cars that fail his test. Normal bidders will get only lemons.
B) $780 for cars that pass his test and $370 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,035 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get only lemons.
D) $600 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $540 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 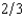of the cars that are auctioned are lemons and 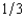are good used cars. A good used car is worth $1,200 to any buyer. A lemon is worth $270 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $735 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get only lemons.
B) $600 for cars that pass his test and $400 for cars that fail his test. Normal bidders will get only lemons.
C) $400 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
D) $580 for cars that pass his test and $370 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $540 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
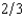of the cars that are auctioned are lemons and 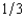are good used cars. A good used car is worth $1,200 to any buyer. A lemon is worth $270 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $735 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get only lemons.
B) $600 for cars that pass his test and $400 for cars that fail his test. Normal bidders will get only lemons.
C) $400 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
D) $580 for cars that pass his test and $370 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $540 for cars that pass his test and $270 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 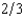of the cars that are auctioned are lemons and 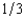are good used cars. A good used car is worth $1,800 to any buyer. A lemon is worth $240 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $1,020 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get only lemons.
B) $900 for cars that pass his test and $600 for cars that fail his test. Normal bidders will get only lemons.
C) $760 for cars that pass his test and $340 for cars that fail his test. Normal bidders will get good cars onlyof the time.
D) $600 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $480 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
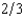of the cars that are auctioned are lemons and 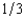are good used cars. A good used car is worth $1,800 to any buyer. A lemon is worth $240 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $1,020 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get only lemons.
B) $900 for cars that pass his test and $600 for cars that fail his test. Normal bidders will get only lemons.
C) $760 for cars that pass his test and $340 for cars that fail his test. Normal bidders will get good cars onlyof the time.
D) $600 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $480 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
Jerry's Auction House in Purloined Hubcap, Oregon, holds sealed-bid used-car auctions every Wednesday. Each car is sold to the highest bidder at the second-highest bidder's bid. On average, 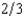of the cars that are auctioned are lemons and 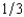are good used cars. A good used car is worth $2,700 to any buyer. A lemon is worth $240 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bid
A) $1,470 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get only lemons.
B) $1,060 for cars that pass his test and $340 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,350 for cars that pass his test and $900 for cars that fail his test. Normal bidders will get only lemons.
D) $900 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $480 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
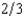of the cars that are auctioned are lemons and 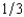are good used cars. A good used car is worth $2,700 to any buyer. A lemon is worth $240 to any buyer. Most buyers can do no better than picking at random from among these used cars. The only exception is Al Crankcase. Recall that Al can sometimes detect lemons by tasting the oil on the car's dipstick. A good car never fails Al's test, but half of the lemons fail his test. Al attends every auction, licks every dipstick, and bids his expected value of every car given the results of his test. Al will bidA) $1,470 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get only lemons.
B) $1,060 for cars that pass his test and $340 for cars that fail his test. Normal bidders will get good cars onlyof the time.
C) $1,350 for cars that pass his test and $900 for cars that fail his test. Normal bidders will get only lemons.
D) $900 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
E) $480 for cars that pass his test and $240 for cars that fail his test. Normal bidders will get good cars onlyof the time.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
