Deck 26: A: Oligopoly
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/30
Play
Full screen (f)
Deck 26: A: Oligopoly
1
In Problem 5, suppose that Grinch and Grubb go into the wine business in a small country where wine is difficult to grow. The demand for wine is given by p = $420 - .2Q, where p is the price and Q is the total quantity sold. The industry consists of just the two Cournot duopolists, Grinch and Grubb. Imports are prohibited. Grinch has constant marginal costs of $60 and Grubb has marginal costs of $30. How much Grinch's output in equilibrium?
A) 275
B) 550
C) 825
D) 1,100
E) 1,650
A) 275
B) 550
C) 825
D) 1,100
E) 1,650
B
2
In Problem 6, suppose that two Cournot duopolists serve the Peoria-Dubuque route, and the demand curve for tickets per day is Q = 250 - 2p (so p = 125 - 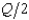 ). Total costs of running a flight on this route are 2,050 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 2,050 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
A) $1,025.
B) $400.
C) $250.
D) $800.
E) $3,850.
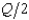 ). Total costs of running a flight on this route are 2,050 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 2,050 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit ofA) $1,025.
B) $400.
C) $250.
D) $800.
E) $3,850.
B
3
If in Problem 4, the inverse demand for bean sprouts were given by P(Y) = 550 - 3Y and the total cost of producing Y units for any firm were TC(Y) = 10Y and if the industry consisted of two Cournot duopolists, then in equilibrium each firm's production would be
A) 90 units.
B) 30 units.
C) 60 units.
D) 45 units.
E) 45.83 units.
A) 90 units.
B) 30 units.
C) 60 units.
D) 45 units.
E) 45.83 units.
C
4
In Problem 6, suppose that two Cournot duopolists serve the Peoria-Dubuque route, and the demand curve for tickets per day is Q = 160 - 2p (so p = 80 - 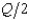 ). Total costs of running a flight on this route are 400 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 400 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
A) $800.
B) $400.
C) $200.
D) $160.
E) $1,600.
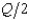 ). Total costs of running a flight on this route are 400 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 400 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit ofA) $800.
B) $400.
C) $200.
D) $160.
E) $1,600.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose that the duopolists Carl and Simon in Problem 1 face a demand function for pumpkins of Q = 8,400 - 800P, where Q is the total number of pumpkins that reach the market and P is the price of pumpkins. Suppose further that each farmer has a constant marginal cost of $.50 for each pumpkin produced. If Carl believes that Simon is going to produce Qs pumpkins this year, then the reaction function tells us how many pumpkins Carl should produce in order to maximize his profits. Carl's reaction function is RC(Qs) =
A) 2,000 -.
B) 8,400 - 800Qs.
C) 8,400 - 1,600Qs.
D) 4,000 -.
E) 6,000 - Qs.
A) 2,000 -.
B) 8,400 - 800Qs.
C) 8,400 - 1,600Qs.
D) 4,000 -.
E) 6,000 - Qs.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
6
In Problem 5, suppose that Grinch and Grubb go into the wine business in a small country where wine is difficult to grow. The demand for wine is given by p = $480 - .2Q, where p is the price and Q is the total quantity sold. The industry consists of just the two Cournot duopolists, Grinch and Grubb. Imports are prohibited. Grinch has constant marginal costs of $6 and Grubb has marginal costs of $45. How much Grinch's output in equilibrium?
A) 675
B) 1,350
C) 337.50
D) 1,012.50
E) 2,025
A) 675
B) 1,350
C) 337.50
D) 1,012.50
E) 2,025

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose that the duopolists Carl and Simon in Problem 1 face a demand function for pumpkins of Q = 16,800 - 800P, where Q is the total number of pumpkins that reach the market and P is the price of pumpkins. Suppose further that each farmer has a constant marginal cost of $1 for each pumpkin produced. If Carl believes that Simon is going to produce Qs pumpkins this year, then the reaction function tells us how many pumpkins Carl should produce in order to maximize his profits. Carl's reaction function is RC(Qs) =
A) 16,800 - 800Qs.
B) 4,000 -.
C) 8,000 -.
D) 16,800 - 1,600Qs.
E) 12,000 - Qs.
A) 16,800 - 800Qs.
B) 4,000 -.
C) 8,000 -.
D) 16,800 - 1,600Qs.
E) 12,000 - Qs.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
8
In Problem 5, suppose that Grinch and Grubb go into the wine business in a small country where wine is difficult to grow. The demand for wine is given by p = $360 - .2Q, where p is the price and Q is the total quantity sold. The industry consists of just the two Cournot duopolists, Grinch and Grubb. Imports are prohibited. Grinch has constant marginal costs of $75 and Grubb has marginal costs of $15. How much Grinch's output in equilibrium?
A) 562.50
B) 187.50
C) 750
D) 375
E) 1,125
A) 562.50
B) 187.50
C) 750
D) 375
E) 1,125

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
9
In Problem 5, suppose that Grinch and Grubb go into the wine business in a small country where wine is difficult to grow. The demand for wine is given by p = $360 - .2Q, where p is the price and Q is the total quantity sold. The industry consists of just the two Cournot duopolists, Grinch and Grubb. Imports are prohibited. Grinch has constant marginal costs of $45 and Grubb has marginal costs of $15. How much Grinch's output in equilibrium?
A) 237.50
B) 712.50
C) 950
D) 475
E) 1,425
A) 237.50
B) 712.50
C) 950
D) 475
E) 1,425

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
10
Suppose that the duopolists Carl and Simon in Problem 1 face a demand function for pumpkins of Q = 16,400 - 400P, where Q is the total number of pumpkins that reach the market and P is the price of pumpkins. Suppose further that each farmer has a constant marginal cost of $1 for each pumpkin produced. If Carl believes that Simon is going to produce Qs pumpkins this year, then the reaction function tells us how many pumpkins Carl should produce in order to maximize his profits. Carl's reaction function is RC(Qs) =
A) 8,000 -.
B) 16,400 - 400Qs.
C) 16,400 - 800Qs.
D) 4,000 -.
E) 12,000 - Qs.
A) 8,000 -.
B) 16,400 - 400Qs.
C) 16,400 - 800Qs.
D) 4,000 -.
E) 12,000 - Qs.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
11
If in Problem 4, the inverse demand for bean sprouts were given by P(Y) = 940 - 5Y and the total cost of producing Y units for any firm were TC(Y) = 40Y and if the industry consisted of two Cournot duopolists, then in equilibrium each firm's production would be
A) 90 units.
B) 45 units.
C) 30 units.
D) 60 units.
E) 47 units.
A) 90 units.
B) 45 units.
C) 30 units.
D) 60 units.
E) 47 units.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
12
Suppose that the duopolists Carl and Simon in Problem 1 face a demand function for pumpkins of Q = 16,800 - 800P, where Q is the total number of pumpkins that reach the market and P is the price of pumpkins. Suppose further that each farmer has a constant marginal cost of $1 for each pumpkin produced. If Carl believes that Simon is going to produce Qs pumpkins this year, then the reaction function tells us how many pumpkins Carl should produce in order to maximize his profits. Carl's reaction function is RC(Qs) =
A) 16,800 - 800Qs.
B) 8,000 -.
C) 16,800 - 1,600Qs.
D) 4,000 -.
E) 12,000 - Qs.
A) 16,800 - 800Qs.
B) 8,000 -.
C) 16,800 - 1,600Qs.
D) 4,000 -.
E) 12,000 - Qs.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose that the duopolists Carl and Simon in Problem 1 face a demand function for pumpkins of Q = 1,800 - 400P, where Q is the total number of pumpkins that reach the market and P is the price of pumpkins. Suppose further that each farmer has a constant marginal cost of $.50 for each pumpkin produced. If Carl believes that Simon is going to produce Qs pumpkins this year, then the reaction function tells us how many pumpkins Carl should produce in order to maximize his profits. Carl's reaction function is RC(Qs) =
A) 1,800 - 400Qs.
B) 1,800 - 800Qs.
C) 800 -.
D) 400 -.
E) 1,200 - Qs.
A) 1,800 - 400Qs.
B) 1,800 - 800Qs.
C) 800 -.
D) 400 -.
E) 1,200 - Qs.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
14
If in Problem 4, the inverse demand for bean sprouts were given by P(Y) = 640 - 3Y and the total cost of producing Y units for any firm were TC(Y) = 10Y and if the industry consisted of two Cournot duopolists, then in equilibrium each firm's production would be
A) 52.50 units.
B) 70 units.
C) 105 units.
D) 35 units.
E) 53.33 units.
A) 52.50 units.
B) 70 units.
C) 105 units.
D) 35 units.
E) 53.33 units.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
15
If in Problem 4, the inverse demand for bean sprouts were given by P(Y) = 430 - 2Y and the total cost of producing Y units for any firm were TC(Y) = 10Y and if the industry consisted of two Cournot duopolists, then in equilibrium each firm's production would be
A) 52.50 units.
B) 70 units.
C) 105 units.
D) 35 units.
E) 53.75 units.
A) 52.50 units.
B) 70 units.
C) 105 units.
D) 35 units.
E) 53.75 units.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
16
In Problem 6, suppose that two Cournot duopolists serve the Peoria-Dubuque route, and the demand curve for tickets per day is Q = 190 - 2p (so p = 95 -  ). Total costs of running a flight on this route are 1,050 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 1,050 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
A) $525.
B) $190.
C) $200.
D) $400.
E) $2,250.
 ). Total costs of running a flight on this route are 1,050 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 1,050 + 20q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit ofA) $525.
B) $190.
C) $200.
D) $400.
E) $2,250.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
17
In Problem 6, suppose that two Cournot duopolists serve the Peoria-Dubuque route, and the demand curve for tickets per day is Q = 240 - 2p (so p = 120 - 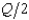 ). Total costs of running a flight on this route are 900 + 30q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 900 + 30q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
A) $240.
B) $900.
C) $1,800.
D) $450.
E) $3,600.
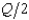 ). Total costs of running a flight on this route are 900 + 30q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 900 + 30q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit ofA) $240.
B) $900.
C) $1,800.
D) $450.
E) $3,600.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
18
In Problem 6, suppose that two Cournot duopolists serve the Peoria-Dubuque route, and the demand curve for tickets per day is Q = 170 - 2p (so p = 85 - 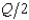 ). Total costs of running a flight on this route are 850 + 10q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 850 + 10q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
A) $400.
B) $425.
C) $170.
D) $800.
E) $1,750.
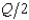 ). Total costs of running a flight on this route are 850 + 10q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit of
). Total costs of running a flight on this route are 850 + 10q, where q is the number of passengers on the flight. Each flight has a capacity of 80 passengers. In Cournot equilibrium, each duopolist will run one flight per day and will make a daily profit ofA) $400.
B) $425.
C) $170.
D) $800.
E) $1,750.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
19
If in Problem 4, the inverse demand for bean sprouts were given by P(Y) = 300 - 3Y and the total cost of producing Y units for any firm were TC(Y) = 30Y and if the industry consisted of two Cournot duopolists, then in equilibrium each firm's production would be
A) 45 units.
B) 22.50 units.
C) 30 units.
D) 15 units.
E) 25 units.
A) 45 units.
B) 22.50 units.
C) 30 units.
D) 15 units.
E) 25 units.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
20
In Problem 5, suppose that Grinch and Grubb go into the wine business in a small country where wine is difficult to grow. The demand for wine is given by p = $480 - .2Q, where p is the price and Q is the total quantity sold. The industry consists of just the two Cournot duopolists, Grinch and Grubb. Imports are prohibited. Grinch has constant marginal costs of $30 and Grubb has marginal costs of $45. How much Grinch's output in equilibrium?
A) 775
B) 1,162.50
C) 387.50
D) 1,550
E) 2,325
A) 775
B) 1,162.50
C) 387.50
D) 1,550
E) 2,325

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
21
There are two firms in the blastopheme industry. The demand curve for blastophemes is given by p = 1,500 - 2q. Each firm has one manufacturing plant and each firm i has a cost function C(qi) = q2i, where qi is the output of firm i. The two firms form a cartel and arrange to split total industry profits equally. Under this cartel arrangement, they will maximize joint profits if
A) and only if each firm produces 150 units in its plant.
B) they produce a total of 300 units, no matter which firm produces them.
C) they produce a total of 250 units, no matter which firm produces them.
D) and only if they each produce a total of 375 units.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.
A) and only if each firm produces 150 units in its plant.
B) they produce a total of 300 units, no matter which firm produces them.
C) they produce a total of 250 units, no matter which firm produces them.
D) and only if they each produce a total of 375 units.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
22
In Problem 4, suppose that the market demand curve for bean sprouts is given by P = 1,660 - 4Q, where P is the price and Q is total industry output. Suppose that the industry has two firms, a Stackleberg leader and a follower. Each firm has a constant marginal cost of $60 per unit of output. In equilibrium, total output by the two firms will be a. 400.
B) 300.
C) 100.
D) 200.
E) 50.
B) 300.
C) 100.
D) 200.
E) 50.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
23
In Problem 4, suppose that the market demand curve for bean sprouts is given by P = 1,480 - 2Q, where P is the price and Q is total industry output. Suppose that the industry has two firms, a Stackleberg leader and a follower. Each firm has a constant marginal cost of $80 per unit of output. In equilibrium, total output by the two firms will be a. 175.
B) 700.
C) 350.
D) 525.
E) 87.50.
B) 700.
C) 350.
D) 525.
E) 87.50.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
24
There are two firms in the blastopheme industry. The demand curve for blastophemes is given by p = 3,000 - 2q. Each firm has one manufacturing plant and each firm i has a cost function C(qi) = q2i, where qi is the output of firm i. The two firms form a cartel and arrange to split total industry profits equally. Under this cartel arrangement, they will maximize joint profits if
A) and only if they each produce a total of 750 units.
B) they produce a total of 500 units, no matter which firm produces them.
C) and only if each firm produces 300 units in its plant.
D) they produce a total of 600 units, no matter which firm produces them.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.
A) and only if they each produce a total of 750 units.
B) they produce a total of 500 units, no matter which firm produces them.
C) and only if each firm produces 300 units in its plant.
D) they produce a total of 600 units, no matter which firm produces them.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
25
In Problem 4, suppose that the market demand curve for bean sprouts is given by P = 3,040 - 3Q, where P is the price and Q is total industry output. Suppose that the industry has two firms, a Stackleberg leader and a follower. Each firm has a constant marginal cost of $40 per unit of output. In equilibrium, total output by the two firms will be a. 1,000.
B) 250.
C) 750.
D) 500.
E) 125.
B) 250.
C) 750.
D) 500.
E) 125.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
26
There are two firms in the blastopheme industry. The demand curve for blastophemes is given by p = 6,600 - 5q. Each firm has one manufacturing plant and each firm i has a cost function C(qi) = q2i, where qi is the output of firm i. The two firms form a cartel and arrange to split total industry profits equally. Under this cartel arrangement, they will maximize joint profits if
A) and only if each firm produces 300 units in its plant.
B) they produce a total of 600 units, no matter which firm produces them.
C) and only if they each produce a total of 660 units.
D) they produce a total of 440 units, no matter which firm produces them.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.
A) and only if each firm produces 300 units in its plant.
B) they produce a total of 600 units, no matter which firm produces them.
C) and only if they each produce a total of 660 units.
D) they produce a total of 440 units, no matter which firm produces them.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
27
In Problem 4, suppose that the market demand curve for bean sprouts is given by P = 1,280 - 4Q, where P is the price and Q is total industry output. Suppose that the industry has two firms, a Stackleberg leader and a follower. Each firm has a constant marginal cost of $80 per unit of output. In equilibrium, total output by the two firms will be a. 150.
B) 75.
C) 225.
D) 300.
E) 37.50.
B) 75.
C) 225.
D) 300.
E) 37.50.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
28
There are two firms in the blastopheme industry. The demand curve for blastophemes is given by p = 4,500 - 4q. Each firm has one manufacturing plant and each firm i has a cost function C(qi) = q2i, where qi is the output of firm i. The two firms form a cartel and arrange to split total industry profits equally. Under this cartel arrangement, they will maximize joint profits if
A) and only if each firm produces 250 units in its plant.
B) they produce a total of 500 units, no matter which firm produces them.
C) and only if they each produce a total of 562.50 units.
D) they produce a total of 375 units, no matter which firm produces them.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.
A) and only if each firm produces 250 units in its plant.
B) they produce a total of 500 units, no matter which firm produces them.
C) and only if they each produce a total of 562.50 units.
D) they produce a total of 375 units, no matter which firm produces them.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
29
There are two firms in the blastopheme industry. The demand curve for blastophemes is given by p = 4,500 - 4q. Each firm has one manufacturing plant and each firm i has a cost function C(qi) = q2i, where qi is the output of firm i. The two firms form a cartel and arrange to split total industry profits equally. Under this cartel arrangement, they will maximize joint profits if
A) they produce a total of 375 units, no matter which firm produces them.
B) and only if each firm produces 250 units in its plant.
C) and only if they each produce a total of 562.50 units.
D) they produce a total of 500 units, no matter which firm produces them.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.
A) they produce a total of 375 units, no matter which firm produces them.
B) and only if each firm produces 250 units in its plant.
C) and only if they each produce a total of 562.50 units.
D) they produce a total of 500 units, no matter which firm produces them.
E) they shut down one of the two plants, having the other operate as a monopoly and splitting the profits.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
30
In Problem 4, suppose that the market demand curve for bean sprouts is given by P = 1,680 - 2Q, where P is the price and Q is total industry output. Suppose that the industry has two firms, a Stackleberg leader and a follower. Each firm has a constant marginal cost of $80 per unit of output. In equilibrium, total output by the two firms will be a. 600.
B) 400.
C) 200.
D) 800.
E) 100.
B) 400.
C) 200.
D) 800.
E) 100.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck



