Deck 24: Strategic Thinking and Game Theory

Question 1

In simultaneous move Bayesian games,a player's beliefs are fully given by the probability distribution used by "Nature" to assign types.

Answer 1

True
In a simultaneous move game,neither player gets any new information as the game unfolds -- and so beliefs at the beginning of the game don't change.

Question 2

A complete information game is a special case of an incomplete information game -- where "Nature" assigns each player a "type" with probability 1.

Answer 2

True
In complete information games,there is no uncertainty about what type of player one is playing.

Question 3

If players discount the future sufficiently,cooperation in infinitely repeated Prisoners' Dilemma games cannot emerge as a subgame perfect equilibrium.

Answer 3

True
In order for cooperation to emerge,players have to think of the long-run benefit from cooperation as outweighing the short run benefit of deviating from cooperation and then "being punished".This requires them not to discount the future too much.

Question 4

If everyone has a dominant strategy in a simultaneous move game,then the action that is played by that strategy is played in all stages of any finitely repeated version of that game in any subgame perfect equilibrium.

Question 5

In mixed strategy Nash equilibria,players play each of two pure strategies with probability 0.5.

Question 6

Suppose a player in a sequential game has 2 potential decision nodes,with 5 possible actions at each node.Then he has 25 possible pure strategies.

Question 7

Any non-credible threat that is part of a Nash equilibrium in a sequential game cannot be played along the Nash equilibrium path.

Question 8

In any subgame perfect equilibrium to an infinitely repeated Prisoners' Dilemma game,the players will end up cooperating.

Question 9

If all players in a game have a dominant strategy,then there can only be one pure strategy Nash equilibrium to the game.

Question 10

If everyone has a dominant strategy,there can be no mixed strategy equilibrium.

Question 11

Complete information sequential games can be represented in payoff matrices and complete information simultaneous games can be represented in game trees with information sets.

Question 12

Suppose a player can play 2 possible actions and has 5 possible decision nodes in a sequential game.Then he has 10 possible strategies he can play.

Question 13

In a simultaneous move game,the number of possible pure strategies a player can play is equal to the number of actions he can choose to take.

Question 14

Cooperation is difficult to achieve in a Prisoners' Dilemma because each player thinks the other player might not cooperate.

Question 15

Every subgame perfect equilibrium is a Nash equilibrium but not every Nash equilibrium is a subgame perfect equilibrium.

Question 16

In a Prisoners' Dilemma,both players are willing to pay to be forced to cooperate.

Question 17

Suppose a player in a sequential game has 5 potential decision nodes,with 2 possible actions at each node.Then he has 25 possible pure strategies.

Question 18

A mixed strategy in which positive probability is placed on more than one action can be a best response to another player's strategy only if the expected payoff from playing the pure strategies (over which the individual is mixing)is the same.

Question 19

In a Bayesian incomplete information game,a "belief" is represented as the probability you place on your opponent playing one strategy versus another.

Question 20

Non-credible threats that are made in a Nash equilibrium (that is not subgame perfect)of a sequential game cannot be made in the first stage by the player who begins the game.

Question 21

If a separating equilibrium is played in a signaling game,the receiver will "update" his beliefs during the game.

Question 22

If a player's strategy in a sequential game is to choose an action that stops the game early on,it is unnecessary to specify that player's plans for moves later on in the game when it would have been his turn to move again.

Question 23

Suppose player 1 potentially moves twice in a sequential game,each time choosing from one of two possible actions -- "Left" or "Right".His first move is at the beginning of the game.He gets to move a second time if he moved "Left" the first time and after observing one of two possible actions by player 2 ("Up" or "Down").But if he moves "Right" in the first stage,he gets no further moves and the game ends after player 2 chooses one of two actions ("Up" or "Down").Draw the game tree and list all possible strategies for players 1 and 2.

Question 24

Consider the following sequential move game: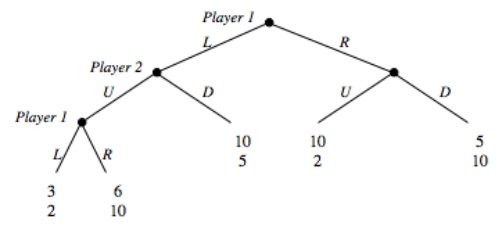
a.What are the subgame perfect equilibrium strategies in this game?
b.List all possible strategies for the two players.
c.Illustrate this game in a payoff matrix.
d.Indicate the Nash equilibria in the payoff matrix from (c).
e.What makes some of the Nash equilibria not subgame perfect?

Question 25

Dominant strategy Nash equilibria are efficient.

Question 26

The Folk Theorem says that anything can happen in infinitely repeated games.

Question 27

If there is no pure strategy Nash equilibrium in a complete information game,there is a mixed strategy equilibrium,and if there is no mixed strategy equilibrium,there is a pure strategy equilibrium.

Question 28

Bayesian updating in a separating equilibrium implies the initially uninformed player will fully know what type he is playing when he has to make his move.

Question 29

Consider player n in a sequential game.
a.If the player can play 2 actions from a single node,how many pure strategies does he have?
b.Suppose he can play 2 actions at each of two different nodes.How many pure strategies does he have now?
c.Suppose he can play 2 actions at each of three different nodes.How many pure strategies does he have now?
d.Suppose he can play 2 actions at each of four different nodes.How many pure strategies does he have now?
e.Suppose he can play 2 actions at each of k different nodes.How many pure strategies does he have now?

Question 30

In a simultaneous move,incomplete information game in which player 1 is unsure of which of two types player 2 is,player 1's strategy must include an action for each possible type that player 2 might be,but player 2 only needs to pick one action since he knows what type he is.

Question 31

If we depict a simultaneous move,complete information game in a game tree,each player only has one information set no matter how many players there are in the game.

Question 32

If a pooling equilibrium is played in a signaling game,the receiver will update her beliefs about the sender before settling on her best option.

Question 33

Consider player n in a sequential game.
a.If the player can play 3 actions from a single node,how many pure strategies does he have?
b.Suppose he can play 3 actions at each of two different nodes.How many pure strategies does he have now?
c.Suppose he can play 3 actions at each of three different nodes.How many pure strategies does he have now?
d.Suppose he can play 3 actions at each of four different nodes.How many pure strategies does he have now?
e.Suppose he can play 3 actions at each of k different nodes.How many pure strategies does he have now?

Question 34

If a pooling equilibrium is played in a signaling game,beliefs about the sender type can take on any form along the branch of the game tree that is not played in equilibrium,but on the branch that is played,beliefs are identical to the probability distribution with which "nature" assigned types to the sender.