Deck 5: The Theory of the Simplex Method
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/4
Play
Full screen (f)
Deck 5: The Theory of the Simplex Method
1
Consider the following problem.Minimize Z = x1 + 2 x2,subject to -x1 + x2 15 2 x1 + x2 90 x2 30 and x1 0,x2 0.
(a)Solve this problem graphically
(b)Develop a table giving each of the CPF solutions and the corresponding defining equations,BF solution,and nonbasic variables.
(a)Solve this problem graphically
(b)Develop a table giving each of the CPF solutions and the corresponding defining equations,BF solution,and nonbasic variables.
(a)Thus,the optimal solution is (x1,x2)= (15,30)with Z = 75. 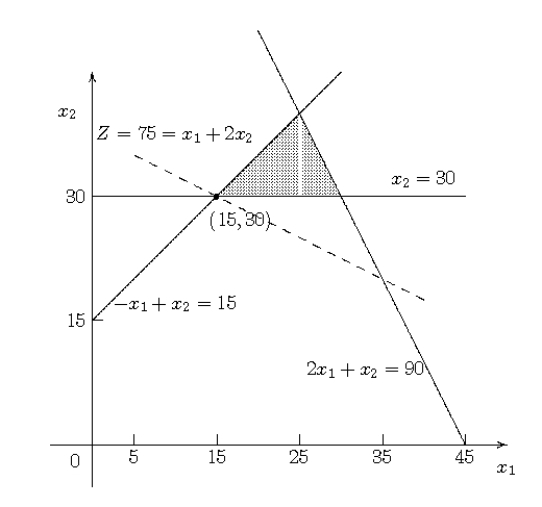 (b)The above graphical solution reveals that the problem has three CPF solutions,as listed in the first column of the table below.The corresponding defining equations are the equations of the constraint boundaries (the solid lines in the above graph)that pass through the respective CPF solutions,as listed in the second column of the table below.To identify the corresponding BF solutions and nonbasic variables,we need to use the augmented form of the problem.Introducing slack variables,x3 and x4,and surplus variable x5,we have Minimize Z = x1 + 2 x2,subject to - x1 + 2 x2 + x3 = 15 2 x1 + x2 + x4 = 90 x2 - x5 = 30 and x1 0,x2 0,x3 0,x4 0,x5 0.Also introducing an artificial variable x6 into the last constraint is optional,since this variable would be needed only to initiate the simplex method,which we are not concerned with doing here.If x6 is introduced,it would become an additional nonbasic variable (so its value would be 0)in the last two columns of the table below.For each CPF solution,the corresponding BF solution listed in the third column is obtained by calculating x3,x4 and x5 in the augmented form of the problem.The nonbasic variables listed in the last column are the variables whose values are 0 in the BF solution.
(b)The above graphical solution reveals that the problem has three CPF solutions,as listed in the first column of the table below.The corresponding defining equations are the equations of the constraint boundaries (the solid lines in the above graph)that pass through the respective CPF solutions,as listed in the second column of the table below.To identify the corresponding BF solutions and nonbasic variables,we need to use the augmented form of the problem.Introducing slack variables,x3 and x4,and surplus variable x5,we have Minimize Z = x1 + 2 x2,subject to - x1 + 2 x2 + x3 = 15 2 x1 + x2 + x4 = 90 x2 - x5 = 30 and x1 0,x2 0,x3 0,x4 0,x5 0.Also introducing an artificial variable x6 into the last constraint is optional,since this variable would be needed only to initiate the simplex method,which we are not concerned with doing here.If x6 is introduced,it would become an additional nonbasic variable (so its value would be 0)in the last two columns of the table below.For each CPF solution,the corresponding BF solution listed in the third column is obtained by calculating x3,x4 and x5 in the augmented form of the problem.The nonbasic variables listed in the last column are the variables whose values are 0 in the BF solution. 
 (b)The above graphical solution reveals that the problem has three CPF solutions,as listed in the first column of the table below.The corresponding defining equations are the equations of the constraint boundaries (the solid lines in the above graph)that pass through the respective CPF solutions,as listed in the second column of the table below.To identify the corresponding BF solutions and nonbasic variables,we need to use the augmented form of the problem.Introducing slack variables,x3 and x4,and surplus variable x5,we have Minimize Z = x1 + 2 x2,subject to - x1 + 2 x2 + x3 = 15 2 x1 + x2 + x4 = 90 x2 - x5 = 30 and x1 0,x2 0,x3 0,x4 0,x5 0.Also introducing an artificial variable x6 into the last constraint is optional,since this variable would be needed only to initiate the simplex method,which we are not concerned with doing here.If x6 is introduced,it would become an additional nonbasic variable (so its value would be 0)in the last two columns of the table below.For each CPF solution,the corresponding BF solution listed in the third column is obtained by calculating x3,x4 and x5 in the augmented form of the problem.The nonbasic variables listed in the last column are the variables whose values are 0 in the BF solution.
(b)The above graphical solution reveals that the problem has three CPF solutions,as listed in the first column of the table below.The corresponding defining equations are the equations of the constraint boundaries (the solid lines in the above graph)that pass through the respective CPF solutions,as listed in the second column of the table below.To identify the corresponding BF solutions and nonbasic variables,we need to use the augmented form of the problem.Introducing slack variables,x3 and x4,and surplus variable x5,we have Minimize Z = x1 + 2 x2,subject to - x1 + 2 x2 + x3 = 15 2 x1 + x2 + x4 = 90 x2 - x5 = 30 and x1 0,x2 0,x3 0,x4 0,x5 0.Also introducing an artificial variable x6 into the last constraint is optional,since this variable would be needed only to initiate the simplex method,which we are not concerned with doing here.If x6 is introduced,it would become an additional nonbasic variable (so its value would be 0)in the last two columns of the table below.For each CPF solution,the corresponding BF solution listed in the third column is obtained by calculating x3,x4 and x5 in the augmented form of the problem.The nonbasic variables listed in the last column are the variables whose values are 0 in the BF solution. 
2
Consider the following problem.Maximize Z = 2x1 + 4x2 + 3x3,subject to x1 + 3x2 + 2x3 ≤ 30 x1 + x2 + x3 ≤ 24 3x1 + 5x2 + 3x3 ≤ 60 and x1 ≥ 0,x2 ≥ 0,x3 ≥ 0.You are given the information that x1 > 0,x2 = 0,and x3 >0 in the optimal solution.Using the given information and the theory of the simplex method,analyze the constraints of the problem in order to identify a system of three constraint boundary equations (defining equations)whose simultaneous solution must be the optimal solution (not augmente d).Then solve this system of equations to obtain this solution.
Since x1 > 0 and x3 > 0,it follows that x1 = 0 and x3 = 0 cannot be part of the three defining equations at the optimal solution.Since x2 = 0,then x1 + x3 24 and 3 x1 + 3 x3 60 or,equivalently,x1 + x3 24 and x1 + x3 20.This implies that the second constraint (x1 + x2 + x3 ≤ 24)must have some slack,so its constraint boundary equation cannot be a defining equation at the optimal solution.We now have ruled out three of the six constraint boundary equations as being part of the defining equations at the optimal solution.For this three-variable problem,each CPF solution including the optimal solution must have three defining equations.Therefore,the three constraint boundary equations not ruled out must be the defining equations for the optimal solution.These defining equations are x2 = 0,x1 + 3 x2 + 2 x3 = 30,3 x1 + 5 x2 + 3 x3 = 60.Solving this system of equations yields the optimal solution as (x1,x2,x3)= (10,0,10).
3
You are using the simplex method to solve the following linear programming problem.Maximize Z = 6x1 + 5x2 - x3 + 4x4,subject to 3x1 + 2x2 - 3x3 + x4 ≤ 120 3x1 + 3x2 + x3 + 3x4 ≤ 180 and x1 ≥ 0,x2 ≥ 0,x3 ≥ 0,x4 ≥ 0.You have obtained the following final simplex tableau where x5 and x6 are the slack variables for the respective constraints. 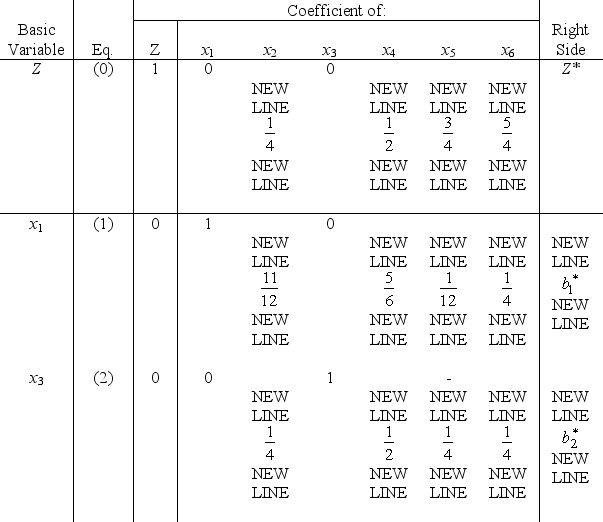 Use the fundamental insight presented in Sec.5.3 of the textbook to identify Z*,
Use the fundamental insight presented in Sec.5.3 of the textbook to identify Z*,  ,and
,and  .
.
 Use the fundamental insight presented in Sec.5.3 of the textbook to identify Z*,
Use the fundamental insight presented in Sec.5.3 of the textbook to identify Z*, 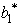 ,and
,and 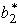 .
.The fundamental insight presented in Sec.5.3 of the textbook states in part that Z* =y*b, 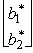 = S*b,where y* =
= S*b,where y* = 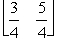 is the vector of coefficients of the slack variables in Eq.(0),S* =
is the vector of coefficients of the slack variables in Eq.(0),S* =  is the matrix of coefficients of the slack variables in the remaining equations,and b is the vector of the original right-hand sides.(Since S = B-1,where B is the basis matrix,and y* = cBB-1,where cB is the vector of the objective function coefficients of the basic variables,this alternative notation may be used throughout this solution.)Therefore,the final right-hand side is
is the matrix of coefficients of the slack variables in the remaining equations,and b is the vector of the original right-hand sides.(Since S = B-1,where B is the basis matrix,and y* = cBB-1,where cB is the vector of the objective function coefficients of the basic variables,this alternative notation may be used throughout this solution.)Therefore,the final right-hand side is 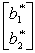 = S* b =
= S* b = 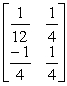
 =
=  ,and Z* = y*b =
,and Z* = y*b = 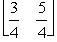
 = 315.
= 315.
 = S*b,where y* =
= S*b,where y* = 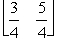 is the vector of coefficients of the slack variables in Eq.(0),S* =
is the vector of coefficients of the slack variables in Eq.(0),S* =  is the matrix of coefficients of the slack variables in the remaining equations,and b is the vector of the original right-hand sides.(Since S = B-1,where B is the basis matrix,and y* = cBB-1,where cB is the vector of the objective function coefficients of the basic variables,this alternative notation may be used throughout this solution.)Therefore,the final right-hand side is
is the matrix of coefficients of the slack variables in the remaining equations,and b is the vector of the original right-hand sides.(Since S = B-1,where B is the basis matrix,and y* = cBB-1,where cB is the vector of the objective function coefficients of the basic variables,this alternative notation may be used throughout this solution.)Therefore,the final right-hand side is  = S* b =
= S* b = 
 =
=  ,and Z* = y*b =
,and Z* = y*b = 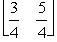
 = 315.
= 315. 4
Consider the following problem.Maximize Z = 2x1 + 4x2 + 3x3,subject to x1 + 3x2 + 2x3 = 20 x1 + 5x2 ≥ 10 and x1 ≥ 0,x2 ≥ 0,x3 ≥ 0.Let 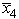 be the artificial variable for the first constraint.Let x5 and
be the artificial variable for the first constraint.Let x5 and 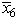 be the surplus variable and artificial variable,respectively,for the second constraint.You are now given the information that a portion of the final simplex tableau is as follows:
be the surplus variable and artificial variable,respectively,for the second constraint.You are now given the information that a portion of the final simplex tableau is as follows: 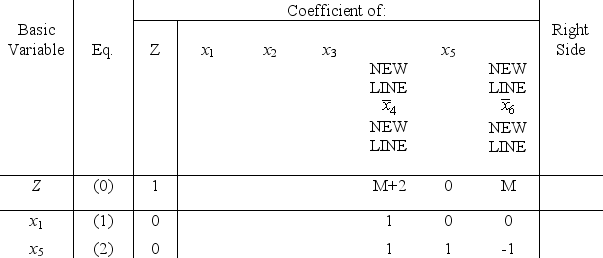 (a)Extend the fundamental insight presented in Sec.5.3 of the textbook to identify the missing numbers in the final simplex tableau.Show your calculations.(b)Identify the defining equations of the CPF solution corresponding to the optimal solution in the final simplex tableau.
(a)Extend the fundamental insight presented in Sec.5.3 of the textbook to identify the missing numbers in the final simplex tableau.Show your calculations.(b)Identify the defining equations of the CPF solution corresponding to the optimal solution in the final simplex tableau.
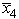 be the artificial variable for the first constraint.Let x5 and
be the artificial variable for the first constraint.Let x5 and 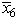 be the surplus variable and artificial variable,respectively,for the second constraint.You are now given the information that a portion of the final simplex tableau is as follows:
be the surplus variable and artificial variable,respectively,for the second constraint.You are now given the information that a portion of the final simplex tableau is as follows:  (a)Extend the fundamental insight presented in Sec.5.3 of the textbook to identify the missing numbers in the final simplex tableau.Show your calculations.(b)Identify the defining equations of the CPF solution corresponding to the optimal solution in the final simplex tableau.
(a)Extend the fundamental insight presented in Sec.5.3 of the textbook to identify the missing numbers in the final simplex tableau.Show your calculations.(b)Identify the defining equations of the CPF solution corresponding to the optimal solution in the final simplex tableau.
Unlock Deck
Unlock for access to all 4 flashcards in this deck.
Unlock Deck
k this deck



