Deck 6: Duality Theory
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/1
Play
Full screen (f)
Deck 6: Duality Theory
For the following linear programming problem,use the SOB method presented in Sec.6.4 of the textbook to construct its dual problem.Minimize Z = 3 x1 + 2 x2, subject to 2 x1 + x2 10 -3 x1 + 2 x2 6 1 x1 + 1 x2 6 and x1 0,x2 0.
The four steps of the SOB method lead to the following conclusions.Step 1: Since the primal problem is in minimization form,the dual problem will be in maximization form.Step 2: Given the minimization form for the primal problem,its first and third functional constraints in ≥ form are labeled as "sensible," as are its two nonnegativity constraints,but the second functional constraint in ≤ form is labeled as "bizarre." Step 3: Because of this labeling of the functional constraints in the primal problem,the first and third variables in the dual problem will have nonnegativity constraints,y1 ≥ 0 and y3 ≥ 0,whereas the second variable will have a nonpositivity constraint, 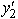 ≤ 0.
≤ 0.
Step 4: Because of the "sensible" labeling for the nonnegativity constraints in the primal problem,the two functional constraints in the dual problem will have the "sensible" ≤ form.Therefore,after placing the numbers in the primal problem in their usual locations for the dual problem,the dual problem is Maximize 10y1 + 6 + 6y3,subject to 2y1 - 3
+ 6y3,subject to 2y1 - 3 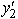 + y3 3 y1 + 2
+ y3 3 y1 + 2 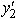 + y3 2 and y1 0,
+ y3 2 and y1 0, 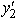 0,y3 0.We can also set the dual variable
0,y3 0.We can also set the dual variable 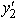 = - y2 with y2 0.Then we obtain an equivalent dual problem: Maximize 10y1 - 6y2 + 6y3,subject to 2y1 + 3y2 + y3 3 y1 - 2y2 + y3 2 and y1 0,y2 0,y3 0
= - y2 with y2 0.Then we obtain an equivalent dual problem: Maximize 10y1 - 6y2 + 6y3,subject to 2y1 + 3y2 + y3 3 y1 - 2y2 + y3 2 and y1 0,y2 0,y3 0
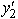 ≤ 0.
≤ 0.Step 4: Because of the "sensible" labeling for the nonnegativity constraints in the primal problem,the two functional constraints in the dual problem will have the "sensible" ≤ form.Therefore,after placing the numbers in the primal problem in their usual locations for the dual problem,the dual problem is Maximize 10y1 + 6
 + 6y3,subject to 2y1 - 3
+ 6y3,subject to 2y1 - 3 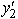 + y3 3 y1 + 2
+ y3 3 y1 + 2 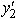 + y3 2 and y1 0,
+ y3 2 and y1 0, 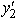 0,y3 0.We can also set the dual variable
0,y3 0.We can also set the dual variable 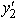 = - y2 with y2 0.Then we obtain an equivalent dual problem: Maximize 10y1 - 6y2 + 6y3,subject to 2y1 + 3y2 + y3 3 y1 - 2y2 + y3 2 and y1 0,y2 0,y3 0
= - y2 with y2 0.Then we obtain an equivalent dual problem: Maximize 10y1 - 6y2 + 6y3,subject to 2y1 + 3y2 + y3 3 y1 - 2y2 + y3 2 and y1 0,y2 0,y3 0 


