Deck 18: Inventory Theory
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/3
Play
Full screen (f)
Deck 18: Inventory Theory
A college student,Stan Ford,recently took a course in operations research.He now enjoys applying what he learned to optimize his personal decisions.He is analyzing one such decision currently,namely,how much money (if any)to take out of his savings account to buy $100 traveler's checks before leaving on a short vacation trip to Europe next summer.Stan already has used the money he had in his checking account to buy traveler's checks worth $1,200,but this may not be enough.In fact,he has estimated the probability distribution of what he will need as shown in the following table: 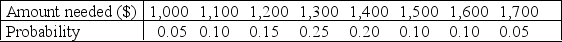 If he turns out to have less than he needs,then he will have to leave Europe 1 day early for every $100 short.Because he places a value of $150 on each day in Europe,each day lost would thereby represent a net loss of $50 to him.However,every $100 traveler's check costs an extra $1.Furthermore,each such check left over at the end of the trip (which would be redeposited in the savings account)represents a loss of $2 in interest that could have been earned in the savings account during the trip,so he does not want to purchase too many.(a)Describe how this problem can be interpreted to be an inventory problem with uncertain demand for a perishable product.Also identify the unit cost of underordering and the unit cost of overordering.(b)Use Bayes' decision rule presented in Sec.16.2 of the textbook to determine how many additional $100 traveler's checks Stan should purchase to minimize his expected cost of underordering or overordering.(c)Recall that the stochastic single-period model for perishable products (as presented in Sec.18.7 of the textbook)finds that the optimal service level is Optimal service level =
If he turns out to have less than he needs,then he will have to leave Europe 1 day early for every $100 short.Because he places a value of $150 on each day in Europe,each day lost would thereby represent a net loss of $50 to him.However,every $100 traveler's check costs an extra $1.Furthermore,each such check left over at the end of the trip (which would be redeposited in the savings account)represents a loss of $2 in interest that could have been earned in the savings account during the trip,so he does not want to purchase too many.(a)Describe how this problem can be interpreted to be an inventory problem with uncertain demand for a perishable product.Also identify the unit cost of underordering and the unit cost of overordering.(b)Use Bayes' decision rule presented in Sec.16.2 of the textbook to determine how many additional $100 traveler's checks Stan should purchase to minimize his expected cost of underordering or overordering.(c)Recall that the stochastic single-period model for perishable products (as presented in Sec.18.7 of the textbook)finds that the optimal service level is Optimal service level = 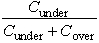 ,where Cunder is the unit cost of underordering and Cover is the unit cost of overordering.Use this result and the table of probabilities to make Stan's decision.d)Draw a graph of the CDF of demand to show the application of the model in part (c)graphically.
,where Cunder is the unit cost of underordering and Cover is the unit cost of overordering.Use this result and the table of probabilities to make Stan's decision.d)Draw a graph of the CDF of demand to show the application of the model in part (c)graphically.
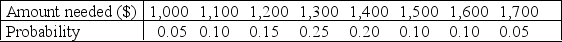 If he turns out to have less than he needs,then he will have to leave Europe 1 day early for every $100 short.Because he places a value of $150 on each day in Europe,each day lost would thereby represent a net loss of $50 to him.However,every $100 traveler's check costs an extra $1.Furthermore,each such check left over at the end of the trip (which would be redeposited in the savings account)represents a loss of $2 in interest that could have been earned in the savings account during the trip,so he does not want to purchase too many.(a)Describe how this problem can be interpreted to be an inventory problem with uncertain demand for a perishable product.Also identify the unit cost of underordering and the unit cost of overordering.(b)Use Bayes' decision rule presented in Sec.16.2 of the textbook to determine how many additional $100 traveler's checks Stan should purchase to minimize his expected cost of underordering or overordering.(c)Recall that the stochastic single-period model for perishable products (as presented in Sec.18.7 of the textbook)finds that the optimal service level is Optimal service level =
If he turns out to have less than he needs,then he will have to leave Europe 1 day early for every $100 short.Because he places a value of $150 on each day in Europe,each day lost would thereby represent a net loss of $50 to him.However,every $100 traveler's check costs an extra $1.Furthermore,each such check left over at the end of the trip (which would be redeposited in the savings account)represents a loss of $2 in interest that could have been earned in the savings account during the trip,so he does not want to purchase too many.(a)Describe how this problem can be interpreted to be an inventory problem with uncertain demand for a perishable product.Also identify the unit cost of underordering and the unit cost of overordering.(b)Use Bayes' decision rule presented in Sec.16.2 of the textbook to determine how many additional $100 traveler's checks Stan should purchase to minimize his expected cost of underordering or overordering.(c)Recall that the stochastic single-period model for perishable products (as presented in Sec.18.7 of the textbook)finds that the optimal service level is Optimal service level = 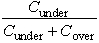 ,where Cunder is the unit cost of underordering and Cover is the unit cost of overordering.Use this result and the table of probabilities to make Stan's decision.d)Draw a graph of the CDF of demand to show the application of the model in part (c)graphically.
,where Cunder is the unit cost of underordering and Cover is the unit cost of overordering.Use this result and the table of probabilities to make Stan's decision.d)Draw a graph of the CDF of demand to show the application of the model in part (c)graphically.(a)This problem can be interpreted as an inventory problem with uncertain demand for a perishable product with traveler's checks as the product.Once Stan gets back from his trip,the remaining checks are of no further use for the trip,so they can be viewed as a perishable product.He can deposit the remaining checks into his savings account but will incur a loss of $2 per check in interest that could have been earned in the savings account during the trip.Stan must decide how many checks to buy without knowing how many he will need.Cunder = value of 1 day - cost of 1 day - cost of 1 check = $49.Cover = cost of 1 check + lost interest = $3.(b)Using Cunder and Cover obtained in part (a),the expected cost of each alternative is calculated in the following table. 
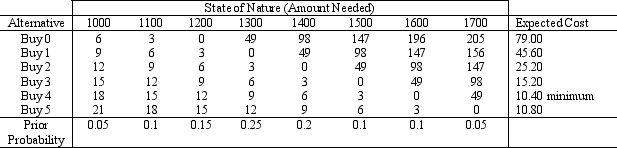 Stan should purchase 4 additional checks.(c)Service level of buying 0 = 0.3.Service level of buying 1 = 0.55.Service level of buying 2 = 0.75.Service level of buying 3 = 0.85.Service level of buying 4 = 0.95.Service level of buying 5 = 1.Optimal service level =
Stan should purchase 4 additional checks.(c)Service level of buying 0 = 0.3.Service level of buying 1 = 0.55.Service level of buying 2 = 0.75.Service level of buying 3 = 0.85.Service level of buying 4 = 0.95.Service level of buying 5 = 1.Optimal service level = 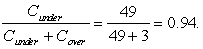 Stan should purchase an additional 4 checks.(d)
Stan should purchase an additional 4 checks.(d) 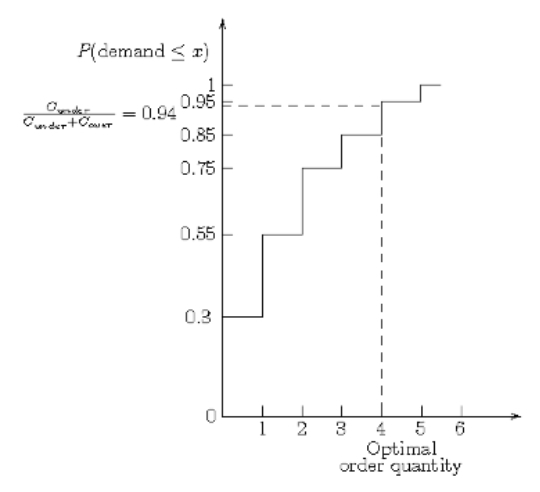

 Stan should purchase 4 additional checks.(c)Service level of buying 0 = 0.3.Service level of buying 1 = 0.55.Service level of buying 2 = 0.75.Service level of buying 3 = 0.85.Service level of buying 4 = 0.95.Service level of buying 5 = 1.Optimal service level =
Stan should purchase 4 additional checks.(c)Service level of buying 0 = 0.3.Service level of buying 1 = 0.55.Service level of buying 2 = 0.75.Service level of buying 3 = 0.85.Service level of buying 4 = 0.95.Service level of buying 5 = 1.Optimal service level = 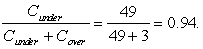 Stan should purchase an additional 4 checks.(d)
Stan should purchase an additional 4 checks.(d) 
Consider the EOQ model with planned shortages,as presented in Sec.18.3 of the textbook.Suppose,however,that the constraint S/Q = 0.8 is added to the model,where Q is the order quantity and S is the inventory level just after a batch of Q units is added to inventory.Derive the expression for the optimal value of Q,using the result for this model that the total cost per unit time is 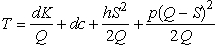 ,where d is the demand rate,K is the setup cost,c is the unit cost of ordering,h is the unit holding cost,and p is the unit shortage cost.
,where d is the demand rate,K is the setup cost,c is the unit cost of ordering,h is the unit holding cost,and p is the unit shortage cost.
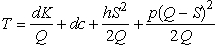 ,where d is the demand rate,K is the setup cost,c is the unit cost of ordering,h is the unit holding cost,and p is the unit shortage cost.
,where d is the demand rate,K is the setup cost,c is the unit cost of ordering,h is the unit holding cost,and p is the unit shortage cost.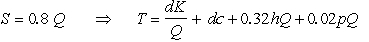 .
. 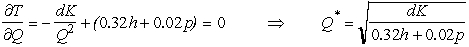 .
.Cindy Stewart and Misty Whitworth graduated from business school together.They now are inventory managers for competing wholesale distributors,making use of the scientific inventory management techniques they learned in school.Both of them are purchasing 85-horsepower speedboat engines for their inventories from the same manufacturer.Cindy has found that the setup cost for initiating each order is $200 and the unit holding cost is $400.Cindy has learned that Misty is ordering 10 engines each time.Cindy assumes that Misty is using the basic EOQ model and has the same setup cost and unit holding cost as Cindy.Show how Cindy can use this information to deduce what the annual demand rate must be for Misty's company for these engines.
Using the EOQ formula, 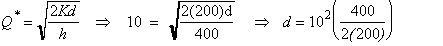 = 100 per year.
= 100 per year.
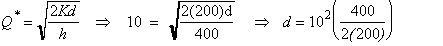 = 100 per year.
= 100 per year.


