Chat with AI
Deck 16: Decision Analysis
Full screen (f)
Question
The General Ford Motors Corporation (GFMC)is planning the introduction of a brand new SUV-the Vector.There are two options for production.One is to build the Vector at the company's existing plant in Indiana,sharing production time with its line of minivans that are currently being produced there.If sales of the Vector are just moderate,this will work out well as there is sufficient capacity to produce both types of vehicles at the same plant.However,if sales of the Vector are strong,this option would require the operation of a third shift,which would lead to significantly higher costs.A second option is to open a new plant in Georgia.This plant would have sufficient capacity to meet even the largest projections for sales of the Vector.However,if sales are only moderate,the plant would be underutilized and therefore less efficient.This is a new design,so sales are hard to predict.However,GFMC predicts that there would be about a 60% chance of strong sales (annual sales of 100,000),and a 40% chance of moderate sales (annual sales of 50,000).The average revenue per Vector sold is $30,000.Production costs per vehicle for the two production options depend upon sales,as indicated in the table below. 
The amortized annual cost of plant construction and other associated fixed costs for the Georgia plant would total $400 million per year (regardless of sales volume).The fixed costs for adding Vector production to the plant in Indiana would total $200 million per year (regardless of sales volume).(a)Construct a decision tree to determine which production option maximizes the expected annual profit,considering fixed costs,production costs,and sales revenues.(b)Due to the uncertainty in expected sales for the Vector,GFMC is considering conducting a marketing survey to determine customer attitudes toward the Vector and better predict the likelihood of strong sales.The marketing survey would give one of two results-a positive attitude or a negative attitude toward the design.GFMC has used this marketing survey for other vehicles.For vehicles that eventually had strong sales,the marketing survey indicated positive attitudes toward the design 70% of the time and negative attitudes 30% of the time.For vehicles that eventually had moderate sales,the marketing survey indicated positive attitudes toward the design 20% of the time and negative attitudes 80% of the time.Assuming GFMC conducts such a survey,construct a decision tree to determine how the company should proceed and what the expected annual profit would be (ignoring the cost of the survey).(c)What is the expected value of experimentation (EVE)in part b? What does this say about how large the cost of the marketing survey can be before it would no longer be worthwhile to conduct the survey?
The amortized annual cost of plant construction and other associated fixed costs for the Georgia plant would total $400 million per year (regardless of sales volume).The fixed costs for adding Vector production to the plant in Indiana would total $200 million per year (regardless of sales volume).(a)Construct a decision tree to determine which production option maximizes the expected annual profit,considering fixed costs,production costs,and sales revenues.(b)Due to the uncertainty in expected sales for the Vector,GFMC is considering conducting a marketing survey to determine customer attitudes toward the Vector and better predict the likelihood of strong sales.The marketing survey would give one of two results-a positive attitude or a negative attitude toward the design.GFMC has used this marketing survey for other vehicles.For vehicles that eventually had strong sales,the marketing survey indicated positive attitudes toward the design 70% of the time and negative attitudes 30% of the time.For vehicles that eventually had moderate sales,the marketing survey indicated positive attitudes toward the design 20% of the time and negative attitudes 80% of the time.Assuming GFMC conducts such a survey,construct a decision tree to determine how the company should proceed and what the expected annual profit would be (ignoring the cost of the survey).(c)What is the expected value of experimentation (EVE)in part b? What does this say about how large the cost of the marketing survey can be before it would no longer be worthwhile to conduct the survey?
Question
An individual makes decisions according to Bayes' decision rule.For her current problem,she has constructed the following payoff table,and she now wishes to maximize the expected payoff. 
The value of x currently is 50,but there is an opportunity to increase x by spending some money now.What is the maximum amount that should be spent to increase x to 75?
The value of x currently is 50,but there is an opportunity to increase x by spending some money now.What is the maximum amount that should be spent to increase x to 75?
Question
Question
Consider the following decision tree,where the probabilities associated with the branches emanating from each event node are shown in parentheses. 
The dollar amount given next to each branch is the cash flow generated along that branch,where these intermediate cash flows add up to the total net cash flow shown to the right of each terminal branch.(The unknown amount for the top branch is represented by the variable x.)The decision maker has a utility function u(y)= 
where y is the total net cash flow after a terminal branch.The resulting utilities for the various terminal branches are shown to the right of the decision tree.Use these utilities to analyze the decision tree.Then determine the value of x for which the decision maker is indifferent between decision alternatives A1 and A2.
The dollar amount given next to each branch is the cash flow generated along that branch,where these intermediate cash flows add up to the total net cash flow shown to the right of each terminal branch.(The unknown amount for the top branch is represented by the variable x.)The decision maker has a utility function u(y)= where y is the total net cash flow after a terminal branch.The resulting utilities for the various terminal branches are shown to the right of the decision tree.Use these utilities to analyze the decision tree.Then determine the value of x for which the decision maker is indifferent between decision alternatives A1 and A2. Question
Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/5
Play
Full screen (f)
Deck 16: Decision Analysis
1
The General Ford Motors Corporation (GFMC)is planning the introduction of a brand new SUV-the Vector.There are two options for production.One is to build the Vector at the company's existing plant in Indiana,sharing production time with its line of minivans that are currently being produced there.If sales of the Vector are just moderate,this will work out well as there is sufficient capacity to produce both types of vehicles at the same plant.However,if sales of the Vector are strong,this option would require the operation of a third shift,which would lead to significantly higher costs.A second option is to open a new plant in Georgia.This plant would have sufficient capacity to meet even the largest projections for sales of the Vector.However,if sales are only moderate,the plant would be underutilized and therefore less efficient.This is a new design,so sales are hard to predict.However,GFMC predicts that there would be about a 60% chance of strong sales (annual sales of 100,000),and a 40% chance of moderate sales (annual sales of 50,000).The average revenue per Vector sold is $30,000.Production costs per vehicle for the two production options depend upon sales,as indicated in the table below. 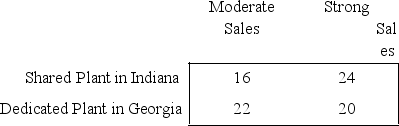The amortized annual cost of plant construction and other associated fixed costs for the Georgia plant would total $400 million per year (regardless of sales volume).The fixed costs for adding Vector production to the plant in Indiana would total $200 million per year (regardless of sales volume).(a)Construct a decision tree to determine which production option maximizes the expected annual profit,considering fixed costs,production costs,and sales revenues.(b)Due to the uncertainty in expected sales for the Vector,GFMC is considering conducting a marketing survey to determine customer attitudes toward the Vector and better predict the likelihood of strong sales.The marketing survey would give one of two results-a positive attitude or a negative attitude toward the design.GFMC has used this marketing survey for other vehicles.For vehicles that eventually had strong sales,the marketing survey indicated positive attitudes toward the design 70% of the time and negative attitudes 30% of the time.For vehicles that eventually had moderate sales,the marketing survey indicated positive attitudes toward the design 20% of the time and negative attitudes 80% of the time.Assuming GFMC conducts such a survey,construct a decision tree to determine how the company should proceed and what the expected annual profit would be (ignoring the cost of the survey).(c)What is the expected value of experimentation (EVE)in part b? What does this say about how large the cost of the marketing survey can be before it would no longer be worthwhile to conduct the survey?
The amortized annual cost of plant construction and other associated fixed costs for the Georgia plant would total $400 million per year (regardless of sales volume).The fixed costs for adding Vector production to the plant in Indiana would total $200 million per year (regardless of sales volume).(a)Construct a decision tree to determine which production option maximizes the expected annual profit,considering fixed costs,production costs,and sales revenues.(b)Due to the uncertainty in expected sales for the Vector,GFMC is considering conducting a marketing survey to determine customer attitudes toward the Vector and better predict the likelihood of strong sales.The marketing survey would give one of two results-a positive attitude or a negative attitude toward the design.GFMC has used this marketing survey for other vehicles.For vehicles that eventually had strong sales,the marketing survey indicated positive attitudes toward the design 70% of the time and negative attitudes 30% of the time.For vehicles that eventually had moderate sales,the marketing survey indicated positive attitudes toward the design 20% of the time and negative attitudes 80% of the time.Assuming GFMC conducts such a survey,construct a decision tree to determine how the company should proceed and what the expected annual profit would be (ignoring the cost of the survey).(c)What is the expected value of experimentation (EVE)in part b? What does this say about how large the cost of the marketing survey can be before it would no longer be worthwhile to conduct the survey?(a)The decision is whether to share the existing plant in Indiana (with a fixed cost of $2 million)or build a new dedicated plant in Georgia (with a fixed cost of $4 million).This decision is represented in the decision tree by a decision node with two branches.For each decision,there are two outcomes: strong sales (60% probability)or moderate sales (40% probability).This is represented in the decision tree by event nodes with two branches.If the Indiana plant is used and sales are strong,the profit would be (100,000 units)($30,000 - $24,000)= $600 million - $200 million (fixed cost)= $400 million.If the Indiana plant is used and sales are moderate,the profit would be (50,000 units)($30,000 - $16,000)= $700 million - $200 million (fixed cost)= $500 million.If the Georgia plant is used and sales are strong,the profit would be (100,000 units)($30,000 - $20,000)= $1000 million - $400 million (fixed cost)= $600 million.If the Georgia plant is used and sales are moderate,the profit would be (50,000 units)($30,000 - $22,000)= $400 million - $400 million (fixed cost)= $0.The resulting solved decision tree is shown below.The decision to share the plant in Indiana has a higher expected profit of $440 million. 
(b)Due to the uncertainty in expected sales for the Vector,GFMC is considering conducting a marketing survey to determine customer attitudes toward the Vector and better predict the likelihood of strong sales.The marketing survey would give one of two results-a positive attitude or a negative attitude toward the design.GFMC has used this marketing survey for other vehicles.For vehicles that eventually had strong sales,the marketing survey indicated positive attitudes toward the design 70% of the time and negative attitudes 30% of the time.For vehicles that eventually had moderate sales,the marketing survey indicated positive attitudes toward the design 20% of the time and negative attitudes 80% of the time.Assuming GFMC conducts such a survey,construct a decision tree to determine how the company should proceed and what the expected annual profit would be (ignoring the cost of the survey).First we must determine an estimate for the probability that the survey will indicate a positive attitude or negative attitude toward the design.Second,given the survey indicates either a positive or negative attitude,we must determine the posterior probability that sales will be either strong or moderate.Both of these calculations can be performed using the template for posterior probabilities provided in the Excel files for Chap.16.These results are shown below.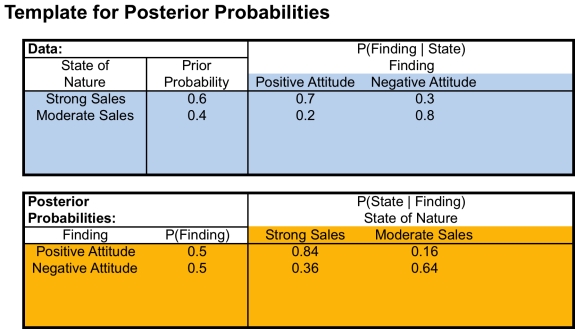 
Thus,there is a 50% chance that the survey will indicate a positive attitude and a 50% chance that the survey will indicate a negative attitude toward the new car.Given a positive attitude,the probability of strong sales increases to 84%.Given a negative attitude,the probability of strong sales sinks to 36%.The revised decision tree is shown below.It begins with an event node with two branches for the two possible outcomes of the survey.After the survey results are known,there is a decision of whether to share the plant in Indiana,or open a new plant in Georgia,represented by a pair of branches.Finally,after the decision is made,there will either be strong or moderate sales.This is represented by event nodes with two branches,and uses the posterior probabilities given the results of the survey. 
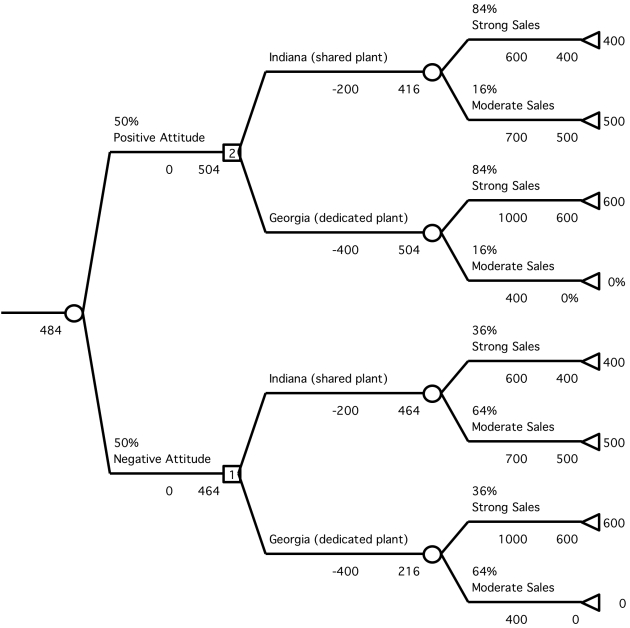If the survey indicates a positive attitude toward the car,they should open a dedicated plant in Georgia.If the survey indicates a negative attitude toward the car,they should share the plant in Indiana.The expected profit is $484 million.(c)The expected value of experimentation is the expected payoff with the information minus the expected payoff without the information.With the survey information,the expected payoff is $484 million.Without the survey information,the expected payoff is $440 million.Thus,the expected value of experimentation in part b is $44 million.This is the most that they should be willing to pay for the marketing survey before it would no longer be worthwhile to conduct.
(b)Due to the uncertainty in expected sales for the Vector,GFMC is considering conducting a marketing survey to determine customer attitudes toward the Vector and better predict the likelihood of strong sales.The marketing survey would give one of two results-a positive attitude or a negative attitude toward the design.GFMC has used this marketing survey for other vehicles.For vehicles that eventually had strong sales,the marketing survey indicated positive attitudes toward the design 70% of the time and negative attitudes 30% of the time.For vehicles that eventually had moderate sales,the marketing survey indicated positive attitudes toward the design 20% of the time and negative attitudes 80% of the time.Assuming GFMC conducts such a survey,construct a decision tree to determine how the company should proceed and what the expected annual profit would be (ignoring the cost of the survey).First we must determine an estimate for the probability that the survey will indicate a positive attitude or negative attitude toward the design.Second,given the survey indicates either a positive or negative attitude,we must determine the posterior probability that sales will be either strong or moderate.Both of these calculations can be performed using the template for posterior probabilities provided in the Excel files for Chap.16.These results are shown below. Thus,there is a 50% chance that the survey will indicate a positive attitude and a 50% chance that the survey will indicate a negative attitude toward the new car.Given a positive attitude,the probability of strong sales increases to 84%.Given a negative attitude,the probability of strong sales sinks to 36%.The revised decision tree is shown below.It begins with an event node with two branches for the two possible outcomes of the survey.After the survey results are known,there is a decision of whether to share the plant in Indiana,or open a new plant in Georgia,represented by a pair of branches.Finally,after the decision is made,there will either be strong or moderate sales.This is represented by event nodes with two branches,and uses the posterior probabilities given the results of the survey. If the survey indicates a positive attitude toward the car,they should open a dedicated plant in Georgia.If the survey indicates a negative attitude toward the car,they should share the plant in Indiana.The expected profit is $484 million.(c)The expected value of experimentation is the expected payoff with the information minus the expected payoff without the information.With the survey information,the expected payoff is $484 million.Without the survey information,the expected payoff is $440 million.Thus,the expected value of experimentation in part b is $44 million.This is the most that they should be willing to pay for the marketing survey before it would no longer be worthwhile to conduct. 2
An individual makes decisions according to Bayes' decision rule.For her current problem,she has constructed the following payoff table,and she now wishes to maximize the expected payoff.
The value of x currently is 50,but there is an opportunity to increase x by spending some money now.What is the maximum amount that should be spent to increase x to 75?
The value of x currently is 50,but there is an opportunity to increase x by spending some money now.What is the maximum amount that should be spent to increase x to 75?
For a1: E[p(a1, )] = 0.4(2x)+ 0.2(50)+0.4(10)= 14 + 0.8x For a2: E[p(a2, )] = 0.4(25)+ 0.2(40)+0.4(90)= 54 For a3: E[p(a3, )] = 0.4(35)+ 0.2(3x)+0.4(30)= 26 + 0.6x At x = 50,the optimal decision alternative is a3,with expected payoff 56.At x = 75,the optimal decision alternative is a1,with expected payoff 74.The minimum amount that should be spent to increase x to 75 is (74 - 56)= 18.
3
You are given the opportunity to guess whether a coin is fair or two-headed,where the prior probabilities are 0.5 for each of these possibilities.If you are correct,you win $5; otherwise,you lose $5.You are also given the option of seeing a demonstration flip of the coin before making your guess.You wish to use Bayes' decision rule to maximize expected profit.(a)Develop a decision analysis formulation of this problem by identifying the decision alternatives,states of nature,and payoff table.(b)What is the optimal decision alternative,given that you decline the option of seeing a demonstration flip? (c)Find EVPI.d)Calculate the posterior distribution if the demonstration flip is a tail.Do the same if the flip is a head.
(e)Determine your optimal policy.(f)Now suppose that you must pay to see the demonstration flip.What is the most that you should be willing to pay? (g)Draw the complete decision tree for this problem and label all the branches.Write the cash flow incurred at each branch or terminal node underneath that branch or node.Write the probability associated with each branch emanating from an event node above that branch.At each decision node,insert a 1 or 2 inside the node to indicate whether the optimal decision there is to choose the upper branch (indicated by a 1)or to choose the lower branch (indicated by a 2).Next to each decision node and event node,write the expected payoff at that node if the optimal policy is being followed.
(e)Determine your optimal policy.(f)Now suppose that you must pay to see the demonstration flip.What is the most that you should be willing to pay? (g)Draw the complete decision tree for this problem and label all the branches.Write the cash flow incurred at each branch or terminal node underneath that branch or node.Write the probability associated with each branch emanating from an event node above that branch.At each decision node,insert a 1 or 2 inside the node to indicate whether the optimal decision there is to choose the upper branch (indicated by a 1)or to choose the lower branch (indicated by a 2).Next to each decision node and event node,write the expected payoff at that node if the optimal policy is being followed.
(a)The decision alternatives are a1: Guess that the coin is fair,a2: Guess that the coin is two-headed.The states of nature are 1: The coin is a fair coin, 2: The coin is a two-headed coin.The payoff table is given below. ![(a)The decision alternatives are a<sub>1</sub>: Guess that the coin is fair,a<sub>2</sub>: Guess that the coin is two-headed.The states of nature are \theta <sub>1</sub>: The coin is a fair coin, \theta <sub>2</sub>: The coin is a two-headed coin.The payoff table is given below. (b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)= = So P(2-headed | flip tail)= 0.P(fair | flip head)= = .So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip tail)] = 1(5)+ 0 (-5)= 5.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a<sub>1</sub>, \theta )| flip tail)] + P(flip head)E[p(a<sub>2</sub>, \theta )| flip head)] = 0.25(5)+ 0.75 = 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g)](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c8be_cd0c_83dc_d95ec1627cc5_TB2462_00.jpg)
(b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)=![(a)The decision alternatives are a<sub>1</sub>: Guess that the coin is fair,a<sub>2</sub>: Guess that the coin is two-headed.The states of nature are \theta <sub>1</sub>: The coin is a fair coin, \theta <sub>2</sub>: The coin is a two-headed coin.The payoff table is given below. (b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)= = So P(2-headed | flip tail)= 0.P(fair | flip head)= = .So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip tail)] = 1(5)+ 0 (-5)= 5.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a<sub>1</sub>, \theta )| flip tail)] + P(flip head)E[p(a<sub>2</sub>, \theta )| flip head)] = 0.25(5)+ 0.75 = 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g)](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c8be_f41d_83dc_bb7b4450da91_TB2462_11.jpg)
= ![(a)The decision alternatives are a<sub>1</sub>: Guess that the coin is fair,a<sub>2</sub>: Guess that the coin is two-headed.The states of nature are \theta <sub>1</sub>: The coin is a fair coin, \theta <sub>2</sub>: The coin is a two-headed coin.The payoff table is given below. (b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)= = So P(2-headed | flip tail)= 0.P(fair | flip head)= = .So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip tail)] = 1(5)+ 0 (-5)= 5.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a<sub>1</sub>, \theta )| flip tail)] + P(flip head)E[p(a<sub>2</sub>, \theta )| flip head)] = 0.25(5)+ 0.75 = 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g)](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c8be_f41e_83dc_9bc16d4d9395_TB2462_11.jpg)
So P(2-headed | flip tail)= 0.P(fair | flip head)= ![(a)The decision alternatives are a<sub>1</sub>: Guess that the coin is fair,a<sub>2</sub>: Guess that the coin is two-headed.The states of nature are \theta <sub>1</sub>: The coin is a fair coin, \theta <sub>2</sub>: The coin is a two-headed coin.The payoff table is given below. (b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)= = So P(2-headed | flip tail)= 0.P(fair | flip head)= = .So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip tail)] = 1(5)+ 0 (-5)= 5.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a<sub>1</sub>, \theta )| flip tail)] + P(flip head)E[p(a<sub>2</sub>, \theta )| flip head)] = 0.25(5)+ 0.75 = 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g)](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c8bf_1b2f_83dc_296e4a535638_TB2462_11.jpg)
= ![(a)The decision alternatives are a<sub>1</sub>: Guess that the coin is fair,a<sub>2</sub>: Guess that the coin is two-headed.The states of nature are \theta <sub>1</sub>: The coin is a fair coin, \theta <sub>2</sub>: The coin is a two-headed coin.The payoff table is given below. (b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)= = So P(2-headed | flip tail)= 0.P(fair | flip head)= = .So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip tail)] = 1(5)+ 0 (-5)= 5.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a<sub>1</sub>, \theta )| flip tail)] + P(flip head)E[p(a<sub>2</sub>, \theta )| flip head)] = 0.25(5)+ 0.75 = 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g)](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c8bf_1b30_83dc_053aaf1fe23b_TB2462_11.jpg)
.So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a1: E[p(a1, | flip tail)] = 1(5)+ 0 (-5)= 5.For a2: E[p(a2, | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a1: E[p(a1, | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a2: E[p(a2, | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a1, )| flip tail)] + P(flip head)E[p(a2, )| flip head)] = 0.25(5)+ 0.75 ![(a)The decision alternatives are a<sub>1</sub>: Guess that the coin is fair,a<sub>2</sub>: Guess that the coin is two-headed.The states of nature are \theta <sub>1</sub>: The coin is a fair coin, \theta <sub>2</sub>: The coin is a two-headed coin.The payoff table is given below. (b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)= = So P(2-headed | flip tail)= 0.P(fair | flip head)= = .So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip tail)] = 1(5)+ 0 (-5)= 5.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a<sub>1</sub>, \theta )| flip tail)] + P(flip head)E[p(a<sub>2</sub>, \theta )| flip head)] = 0.25(5)+ 0.75 = 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g)](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c8bf_4241_83dc_bf6d201d015b_TB2462_11.jpg)
= 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g) ![(a)The decision alternatives are a<sub>1</sub>: Guess that the coin is fair,a<sub>2</sub>: Guess that the coin is two-headed.The states of nature are \theta <sub>1</sub>: The coin is a fair coin, \theta <sub>2</sub>: The coin is a two-headed coin.The payoff table is given below. (b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)= = So P(2-headed | flip tail)= 0.P(fair | flip head)= = .So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip tail)] = 1(5)+ 0 (-5)= 5.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a<sub>1</sub>: E[p(a<sub>1</sub>, \theta | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a<sub>2</sub>: E[p(a<sub>2</sub>, \theta | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a<sub>1</sub>, \theta )| flip tail)] + P(flip head)E[p(a<sub>2</sub>, \theta )| flip head)] = 0.25(5)+ 0.75 = 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g)](https://d2lvgg3v3hfg70.cloudfront.net/TB2462/11ea84c6_c8bf_6952_83dc_afc5c5a8b7e0_TB2462_00.jpg)
(b)The two decision alternatives tie for being optimal,since both give an expected payoff of $0.(c)The expected payoff with perfect information is 0.5(5)+ 0.5(5)= 5.Therefore,since the expected payoff without experimentation is 0,EVPI = 5 - 0 = 5.(d)P(fair | flip tail)=
= So P(2-headed | flip tail)= 0.P(fair | flip head)= = .So P(2-headed | flip head)= 2/3.(e)If flipped tail: For a1: E[p(a1, | flip tail)] = 1(5)+ 0 (-5)= 5.For a2: E[p(a2, | flip tail)] = 1(-5)+ 0 (5)= -5.If flipped head: For a1: E[p(a1, | flip head)] = (1/3)(5)+ (2/3)(-5)= -5/3.For a2: E[p(a2, | flip head)] = (1/3)(-5)+ (2/3)(5)= 5/3.So,if tail occurs,guess fair coin; if head occurs,guess 2-headed coin.(f)P(flip tail)= P(flip tail | fair)P(fair)+ P(flip tail | 2-headed)P(2-headed)= 0.5(0.5)+ 0(0.5)= 0.25,so P(flip head)= 1 - P(flip tail)= 0.75.Therefore,using the optimal policy from part (e),the expected payoff with experimentation is P(flip tail)E[p(a1, )| flip tail)] + P(flip head)E[p(a2, )| flip head)] = 0.25(5)+ 0.75 = 2.5.Since the expected payoff without experimentation is 0,the expected value of experimentation is EVE = 2.5 - 0 = 2.5.Consequently,the most you should be willing to pay to see the demonstration flip is $2.50.(g) 4
Consider the following decision tree,where the probabilities associated with the branches emanating from each event node are shown in parentheses. 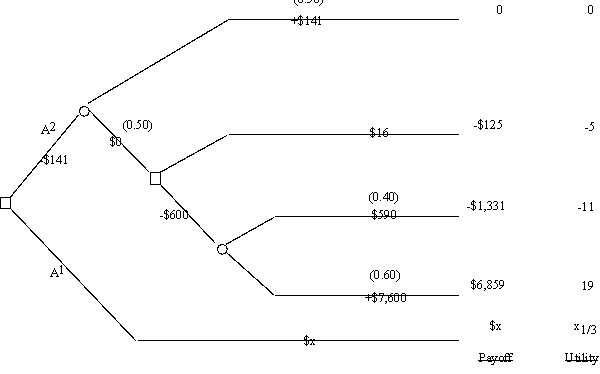The dollar amount given next to each branch is the cash flow generated along that branch,where these intermediate cash flows add up to the total net cash flow shown to the right of each terminal branch.(The unknown amount for the top branch is represented by the variable x.)The decision maker has a utility function u(y)= 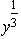where y is the total net cash flow after a terminal branch.The resulting utilities for the various terminal branches are shown to the right of the decision tree.Use these utilities to analyze the decision tree.Then determine the value of x for which the decision maker is indifferent between decision alternatives A1 and A2.
The dollar amount given next to each branch is the cash flow generated along that branch,where these intermediate cash flows add up to the total net cash flow shown to the right of each terminal branch.(The unknown amount for the top branch is represented by the variable x.)The decision maker has a utility function u(y)= 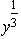where y is the total net cash flow after a terminal branch.The resulting utilities for the various terminal branches are shown to the right of the decision tree.Use these utilities to analyze the decision tree.Then determine the value of x for which the decision maker is indifferent between decision alternatives A1 and A2. Unlock Deck
Unlock for access to all 5 flashcards in this deck.
Unlock Deck
k this deck
5
Meredith Delgado owns a small firm that has developed software for organizing and playing music on a computer.Her software contains a number of unique features that she has patented so her company's future has looked bright.However,there now has been an ominous development.It appears that a number of her patented features were copied in similar software developed by MusicMan Software,a huge software company with annual sales revenue in excess of $1 billion.Meredith is distressed.MusicMan Software has stolen her ideas and that company's marketing power is likely to enable it to capture the market and drive Meredith out of business.In response,Meredith has sued MusicMan Software for patent infringement.With attorney fees and other expenses,the cost of going to trial (win or lose)is expected to be $1 million.She feels that she has a 60% chance of winning the case,in which case she would receive $5 million in damages.If she loses the case,she gets nothing.Moreover,if she loses the case,there is a 50% chance that the judge would also order Meredith to pay for court expenses and lawyer fees for MusicMan (an additional $1 million cost).Music Man Software has offered Meredith $1.5 million to settle this case out of court.(a)Construct and use a decision tree to determine whether Meredith should go to court or accept the settlement offer,assuming she wants to maximize her expected payoff.(b)To implement the equivalent lottery method to determine appropriate utility values for all the possible payoffs in this problem,what questions would need to be asked of Meredith? (c)Suppose that Meredith's attitude toward risk is such that she would be indifferent between doing nothing and a gamble where she would win $1 million with 50% probability and lose $500 thousand with 50% probability.Use the exponential utility function to re-solve the decision tree from part a.
Unlock Deck
Unlock for access to all 5 flashcards in this deck.
Unlock Deck
k this deck
Unlock Deck
Unlock for access to all 5 flashcards in this deck.
