Deck 13: Queuing Theory
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/87
Play
Full screen (f)
Deck 13: Queuing Theory
1
Which type of queuing system are you likely to encounter at a grocery store?
A)Single waiting line,single service station.
B)Multiple waiting lines,single service station.
C)Single waiting line,multiple service stations.
D)Multiple waiting lines,multiple service stations.
A)Single waiting line,single service station.
B)Multiple waiting lines,single service station.
C)Single waiting line,multiple service stations.
D)Multiple waiting lines,multiple service stations.
D
2
What is the formula for Pt ≤ T)under the exponential distribution with rate μ?
A)1 − eμT
B)eμT
C)1 − e−μT
D)1 − eT
A)1 − eμT
B)eμT
C)1 − e−μT
D)1 − eT
C
3
If the number of arrivals in a time period follow a Poisson distribution with mean λ then the inter-arrival times follow an)distribution with mean .
A)normal;μ
B)constant;λ
C)exponential;λ
D)exponential;1/λ
A)normal;μ
B)constant;λ
C)exponential;λ
D)exponential;1/λ
D
4
Which type of queuing system are you likely to encounter at an ATM?
A)Single waiting line,single service station.
B)Multiple waiting lines,single service station.
C)Single waiting line,multiple service stations.
D)Multiple waiting lines,multiple service stations.
A)Single waiting line,single service station.
B)Multiple waiting lines,single service station.
C)Single waiting line,multiple service stations.
D)Multiple waiting lines,multiple service stations.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following is a reason to employ queuing theory?
A)To reduce customer wait time in line.
B)To reduce service times.
C)To generate more arrivals to the system.
D)To reduce worker idle time in line.
A)To reduce customer wait time in line.
B)To reduce service times.
C)To generate more arrivals to the system.
D)To reduce worker idle time in line.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following is the typical operating characteristic for average number of units in a queue?
A)W
B)Wq
C)L
D)Lq
A)W
B)Wq
C)L
D)Lq

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following is the typical operating characteristic for average time a unit spends waiting for service?
A)W
B)Wq
C)L
D)Lq
A)W
B)Wq
C)L
D)Lq

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
8
If the service rate decreases as the arrival rate remains constant,then,in general
A)customer waiting time increases.
B)customer waiting time decreases.
C)service costs increase.
D)customer dissatisfaction decreases.
A)customer waiting time increases.
B)customer waiting time decreases.
C)service costs increase.
D)customer dissatisfaction decreases.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
9
If cell B2 contains the value for ? and cell A5 contains the value for T,what formula should go in cell B5 to compute the PService time)? T for this exponential distribution?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
10
The memoryless property is also referred to as the property.
A)Markov
B)Erlang
C)Poisson
D)Normal
A)Markov
B)Erlang
C)Poisson
D)Normal

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
11
What is the mean arrival rate based on the following 8 arrival rate observations?
Number of arrivals per hour: 6,5,3,4,7,6,4,5
A)3
B)4
C)5
D)6
Number of arrivals per hour: 6,5,3,4,7,6,4,5
A)3
B)4
C)5
D)6

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following best describes queuing theory?
A)The study of arrival rates.
B)The study of service times.
C)The study of waiting lines.
D)The evaluation of service time costs.
A)The study of arrival rates.
B)The study of service times.
C)The study of waiting lines.
D)The evaluation of service time costs.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
13
An arrival process is memoryless if
A)the time until the next arrival depends on the time elapsed since the last arrival.
B)the time until the next arrival is based on the time elapsed since the last arrival.
C)the time until the next arrival does not depend on the time elapsed since the last arrival.
D)the time until the next arrival is based on the arrival rate.
A)the time until the next arrival depends on the time elapsed since the last arrival.
B)the time until the next arrival is based on the time elapsed since the last arrival.
C)the time until the next arrival does not depend on the time elapsed since the last arrival.
D)the time until the next arrival is based on the arrival rate.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
14
For a Poisson random variable,λ represents the number of arrivals per time period
A)maximum
B)minimum
C)average
D)standard deviation of
A)maximum
B)minimum
C)average
D)standard deviation of

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
15
The number of arrivals to a store follows a Poisson distribution with mean λ = 10/hour.What is the mean inter-arrival time?
A)6 seconds
B)6 minutes
C)10 minutes
D)10 hours
A)6 seconds
B)6 minutes
C)10 minutes
D)10 hours

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
16
A Poisson distribution shape can be described as
A)slightly skewed to the left.
B)symmetric around the parameter λ.
C)skewed to the right.
D)discrete so it lacks any definable shape.
A)slightly skewed to the left.
B)symmetric around the parameter λ.
C)skewed to the right.
D)discrete so it lacks any definable shape.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
17
What is the service policy in the queuing systems presented in this chapter that is considered "fair" by the customers?
A)FIFO
B)LIFO
C)FILO
D)Priority
A)FIFO
B)LIFO
C)FILO
D)Priority

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
18
Which type of queuing system are you likely to encounter at a Wendy's restaurant?
A)Single waiting line,single service station.
B)Multiple waiting lines,single service station.
C)Single waiting line,multiple service stations.
D)Multiple waiting lines,multiple service stations.
A)Single waiting line,single service station.
B)Multiple waiting lines,single service station.
C)Single waiting line,multiple service stations.
D)Multiple waiting lines,multiple service stations.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following is the typical operating characteristic for the probability an arriving unit has to wait for service?
A)Wp
B)P0
C)Pw
D)Pn
A)Wp
B)P0
C)Pw
D)Pn

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
20
If the arrival process is modeled as a Poisson random variable with arrival rate λ,then the average time between arrivals is
A)1/μ
B)1/λ
C)1/λ2
D)σ
A)1/μ
B)1/λ
C)1/λ2
D)σ

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
21
A company has recorded the following list of service rates customers/hour)for one of its servers.What is the mean service time for this server?
Customers / hour: 4,4,5,6,5,4,3,4,3,5,5,6
A)0.22 min
B)1.11 min
C)4.5 min
D)13.3 min
Customers / hour: 4,4,5,6,5,4,3,4,3,5,5,6
A)0.22 min
B)1.11 min
C)4.5 min
D)13.3 min

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
22
The service times for a grocery store with one checkout line have a mean of 3 minutes and a standard deviation of 20 seconds.Customer arrivals at the checkout stand follow a Poisson distribution.What type of system is it?
A)M/G/1
B)M/D/1
C)G/M/1
D)M/M/1
A)M/G/1
B)M/D/1
C)G/M/1
D)M/M/1

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
23
If a service system has a constant service time,Poisson arrival rates and 2 servers its Kendall notation is
A)P/D/2
B)M/D/2
C)M/D/1
D)G/D/2
A)P/D/2
B)M/D/2
C)M/D/1
D)G/D/2

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
24
A doctor's office only has 8 chairs.The doctor's service times and customer inter-arrival times are exponentially distributed.What type of system is it?
A)M/M/1
B)M/M/8
C)M/M/1 with Finite Queue
D)M/M/1 with Finite Population
A)M/M/1
B)M/M/8
C)M/M/1 with Finite Queue
D)M/M/1 with Finite Population

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
25
Exhibit 13.1
The following questions are based on the output below.
A store currently operates its service system with 1 operator.Arrivals follow a Poisson distribution and service times are exponentially distributed.The following spreadsheet has been developed for the system.

Refer to Exhibit 13.1.What is the probability that a customer can go directly into service without waiting in line?
A)0.00
B)0.25
C)0.75
D)1.00
The following questions are based on the output below.
A store currently operates its service system with 1 operator.Arrivals follow a Poisson distribution and service times are exponentially distributed.The following spreadsheet has been developed for the system.

Refer to Exhibit 13.1.What is the probability that a customer can go directly into service without waiting in line?
A)0.00
B)0.25
C)0.75
D)1.00

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
26
The M/D/1 model results can be derived from which of the following systems?
A)M/M/1 with λ = 0
B)M/G/1 with μ = 0
C)M/G/1 with σ = 0
D)M/M/2 with finite queue length.
A)M/M/1 with λ = 0
B)M/G/1 with μ = 0
C)M/G/1 with σ = 0
D)M/M/2 with finite queue length.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
27
If a company adds an additional identical server to its M/M/1 system,making an M/M/2 system,what happens to a customer's average service time?
A)increases
B)decreases
C)it is unchanged
D)depends on the arrival rate
A)increases
B)decreases
C)it is unchanged
D)depends on the arrival rate

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
28
Exhibit 13.1
The following questions are based on the output below.
A store currently operates its service system with 1 operator.Arrivals follow a Poisson distribution and service times are exponentially distributed.The following spreadsheet has been developed for the system.

Refer to Exhibit 13.1.What is the probability that a customer must wait in queue before being served?
A)0.00
B)0.25
C)0.75
D)1.00
The following questions are based on the output below.
A store currently operates its service system with 1 operator.Arrivals follow a Poisson distribution and service times are exponentially distributed.The following spreadsheet has been developed for the system.

Refer to Exhibit 13.1.What is the probability that a customer must wait in queue before being served?
A)0.00
B)0.25
C)0.75
D)1.00

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
29
A barber shop has one barber,a Poisson arrival rate and exponentially distributed service times.What is the Kendall notation for this system?
A)M/M/E
B)M/M/1
C)M/E/1
D)P/M/1
A)M/M/E
B)M/M/1
C)M/E/1
D)P/M/1

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
30
Exhibit 13.1
The following questions are based on the output below.
A store currently operates its service system with 1 operator.Arrivals follow a Poisson distribution and service times are exponentially distributed.The following spreadsheet has been developed for the system.

Refer to Exhibit 13.1.How many customers will be in the store on average at any one time?
A)0.375
B)0.50
C)2.25
D)3.00
The following questions are based on the output below.
A store currently operates its service system with 1 operator.Arrivals follow a Poisson distribution and service times are exponentially distributed.The following spreadsheet has been developed for the system.

Refer to Exhibit 13.1.How many customers will be in the store on average at any one time?
A)0.375
B)0.50
C)2.25
D)3.00

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
31
Joe's Copy Center has 10 copiers.They break down and require service quite often.Time between breakdowns follows an exponential distribution for each copier.The repair person services machines as quickly as possible,but the service time follows an exponential distribution.What type of system is it?
A)M/M/1 with Finite Population
B)M/M/1 with Finite Queue
C)M/M/1
D)M/M/10
A)M/M/1 with Finite Population
B)M/M/1 with Finite Queue
C)M/M/1
D)M/M/10

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
32
A renege refers to
A)a customer who refuses to join the queue.
B)a customer who refuses service by a specific server.
C)a customer who joins the queue but leaves before service is complete.
D)a customer who requires extra service time.
A)a customer who refuses to join the queue.
B)a customer who refuses service by a specific server.
C)a customer who joins the queue but leaves before service is complete.
D)a customer who requires extra service time.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
33
The amount of time a customer spends with the server is referred to as
A)system time.
B)queue time.
C)service time.
D)served time.
A)system time.
B)queue time.
C)service time.
D)served time.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
34
A balk refers to
A)a customer who refuses to join the queue.
B)a customer who refuses service by a specific server.
C)a customer who joins the queue but leaves before service is complete.
D)a customer who requires extra service time.
A)a customer who refuses to join the queue.
B)a customer who refuses service by a specific server.
C)a customer who joins the queue but leaves before service is complete.
D)a customer who requires extra service time.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
35
A store is considering adding a second clerk.The customer arrival rate at this new server will be
A)twice the old rate.
B)half the old rate.
C)the same as the old rate.
D)unpredictable.
A)twice the old rate.
B)half the old rate.
C)the same as the old rate.
D)unpredictable.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
36
Joe's Copy Center has 10 copiers.They break down at a rate of 0.02 copiers per hour and are sent to the service facility.What is the average arrival rate of broken copiers to the service facility?
A)0.02
B)0.2
C)10
D)It cannot be determined from the information provided.
A)0.02
B)0.2
C)10
D)It cannot be determined from the information provided.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
37
The M in M/G/1 stands for
A)Markovian inter-arrival times.
B)Mendelian inter-arrival times.
C)Mean inter-arrival times.
D)Mathematical inter-arrival times.
A)Markovian inter-arrival times.
B)Mendelian inter-arrival times.
C)Mean inter-arrival times.
D)Mathematical inter-arrival times.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
38
Exhibit 13.1
The following questions are based on the output below.
A store currently operates its service system with 1 operator.Arrivals follow a Poisson distribution and service times are exponentially distributed.The following spreadsheet has been developed for the system.

Refer to Exhibit 13.1.What is average amount of time spent waiting in line?
A)0.375
B)0.50
C)2.25
D)3.00
The following questions are based on the output below.
A store currently operates its service system with 1 operator.Arrivals follow a Poisson distribution and service times are exponentially distributed.The following spreadsheet has been developed for the system.

Refer to Exhibit 13.1.What is average amount of time spent waiting in line?
A)0.375
B)0.50
C)2.25
D)3.00

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
39
To find steady-state values for the M/M/S queuing system,which of the following statements must be true about the arrival rate?
A)λ < s μ
B)λ − s = μ
C)λ > s μ
D)λ = s μ
A)λ < s μ
B)λ − s = μ
C)λ > s μ
D)λ = s μ

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
40
The standardized queuing system notation such as M/M/1 or M/G/2 is referred to as
A)Kendall notation.
B)Erlang notation.
C)Poisson notation.
D)Queuing notation.
A)Kendall notation.
B)Erlang notation.
C)Poisson notation.
D)Queuing notation.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
41
Exhibit 13.
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.
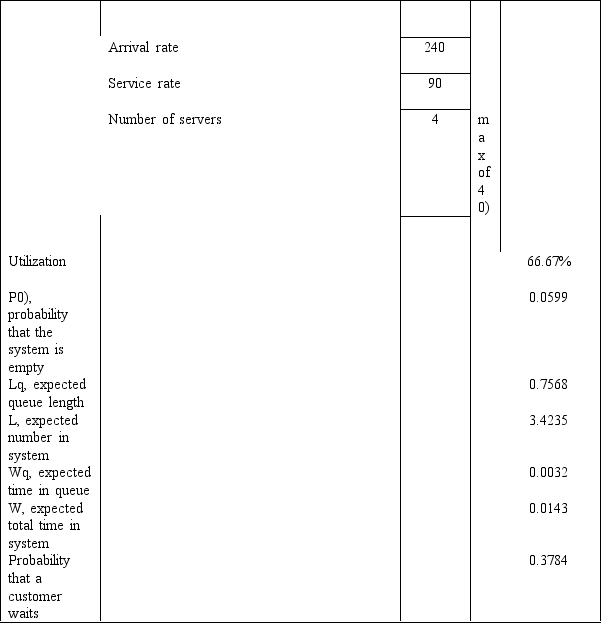
Refer to Exhibit 13.4.What is the Kendall notation for this system?
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.What is the Kendall notation for this system?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
42
A grocery clerk can serve 20 customers per hour on average and the service time follows an exponential distribution.What is the probability that a customer's service time is more than 4 minutes?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 13.3
The following questions refer to the information below.
A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines.Assume the data are exponentially distributed and the 10 data points represent a reasonable sample.
All time in minutes
-Refer to Exhibit 13.3.What is the average time a customer spends in the service line?
The following questions refer to the information below.
A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines.Assume the data are exponentially distributed and the 10 data points represent a reasonable sample.
All time in minutes
-Refer to Exhibit 13.3.What is the average time a customer spends in the service line?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
44
Exhibit 13.2
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.Based on this report what percent of the time is the barber busy cutting hair?
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.Based on this report what percent of the time is the barber busy cutting hair?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
45
Exhibit 13.2
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.What is the Kendall notation for this system?
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.What is the Kendall notation for this system?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
46
Customers arrive at a store randomly,following a Poisson distribution at an average rate of 90 per hour.How many customers arrive per minute,on average?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
47
Exhibit 13.3
The following questions refer to the information below.
A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines.Assume the data are exponentially distributed and the 10 data points represent a reasonable sample.
All time in minutes
-Refer to Exhibit 13.3.What is the mean arrival rate per hour?
The following questions refer to the information below.
A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines.Assume the data are exponentially distributed and the 10 data points represent a reasonable sample.
All time in minutes
-Refer to Exhibit 13.3.What is the mean arrival rate per hour?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
48
Customers arrive at a store randomly,following a Poisson distribution at an average rate of 90 per hour.How many customers would you expect to arrive in a 20 minute period?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
49
The customer service desk at Joe's Discount Electronics store receives 5 customers per hour on average.On average,each customer requires 10 minutes for service.The customer service desk is staffed by a single person.What is the average time a customer spends in the customer service area if modeled as an M/M/1 queuing system?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
50
A grocery clerk can serve 20 customers per hour on average and the service time follows an exponential distribution.What is the expected service time per customer?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
51
Exhibit 13.2
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.Based on this report what is the average number of customers waiting for a haircut?
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.Based on this report what is the average number of customers waiting for a haircut?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
52
Exhibit 13.2
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.Based on this report what is the average waiting time before the barber begins a customer's haircut?
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.Based on this report what is the average waiting time before the barber begins a customer's haircut?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
53
Customers arrive at a store randomly,following a Poisson distribution at an average rate of 20 per hour.What is the probability of exactly 0,1 2,and 3 arrivals in a 15 minute period?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
54
A jockey refers to
A)a customer who refuses to join the queue.
B)a customer who refuses service by a specific server.
C)a customer who joins the queue but leaves before service is complete.
D)a customer who switches between queues in the system.
A)a customer who refuses to join the queue.
B)a customer who refuses service by a specific server.
C)a customer who joins the queue but leaves before service is complete.
D)a customer who switches between queues in the system.

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
55
Exhibit 13.3
The following questions refer to the information below.
A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines.Assume the data are exponentially distributed and the 10 data points represent a reasonable sample.
All time in minutes
-Refer to Exhibit 13.3.What is the mean service rate per hour?
The following questions refer to the information below.
A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines.Assume the data are exponentially distributed and the 10 data points represent a reasonable sample.
All time in minutes
-Refer to Exhibit 13.3.What is the mean service rate per hour?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
56
A grocery clerk can serve 20 customers per hour on average and the service time follows an exponential distribution.What is the probability that a customer's service time is less than 2 minutes?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
57
Exhibit 13.3
The following questions refer to the information below.
A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines.Assume the data are exponentially distributed and the 10 data points represent a reasonable sample.
All time in minutes
-Refer to Exhibit 13.3.What is the average number of customers in the service line?
The following questions refer to the information below.
A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines.Assume the data are exponentially distributed and the 10 data points represent a reasonable sample.
All time in minutes
-Refer to Exhibit 13.3.What is the average number of customers in the service line?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
58
The customer service desk at Joe's Discount Electronics store receives 5 customers per hour on average.On average,each customer requires 10 minutes for service.The customer service desk is staffed by a single person.What is the average number of customers in the customer service area,if modeled as an M/M/1 queuing system?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
59
A company has recorded the following list of service rates customers/hour)for one of its servers.What is the mean service time for this server?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
60
Exhibit 13.2
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.Based on this report what is the average total time spent waiting for a haircut and getting a haircut?
The following questions refer to the information and output below.
A barber shop has one barber who can give 12 haircuts per hour.Customers arrive at a rate of 8 customers per hour.Customer inter-arrival times and service times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
Refer to Exhibit 13.2.Based on this report what is the average total time spent waiting for a haircut and getting a haircut?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
61
Exhibit 13.
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.Based on this report what is the average total time spent in line and being checked out?
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.Based on this report what is the average total time spent in line and being checked out?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
62
Exhibit 13.
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.Based on this report how long does a customer wait before the checker begins serving them?
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.Based on this report how long does a customer wait before the checker begins serving them?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
63
Exhibit 13.
The following questions refer to the information and output below.
The university computer lab has 10 computers which are constantly being used by students.Users need help from the one lab assistant fairly often.Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer.The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.6.What is the Kendall notation for this system?
The following questions refer to the information and output below.
The university computer lab has 10 computers which are constantly being used by students.Users need help from the one lab assistant fairly often.Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer.The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.6.What is the Kendall notation for this system?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
64
A common queue discipline used in practice is
A)first-in-first-out
B)random
C)last-in-first-out
D)group arrival
A)first-in-first-out
B)random
C)last-in-first-out
D)group arrival

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
65
Exhibit 13.
The following questions refer to the information and output below.
A computer printer in a large administrative office has a printer buffer memory to store printing jobs)capacity of 3 jobs.If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later.There are so many users in this office that we can assume that there is an infinite calling population.Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print.Printing times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.
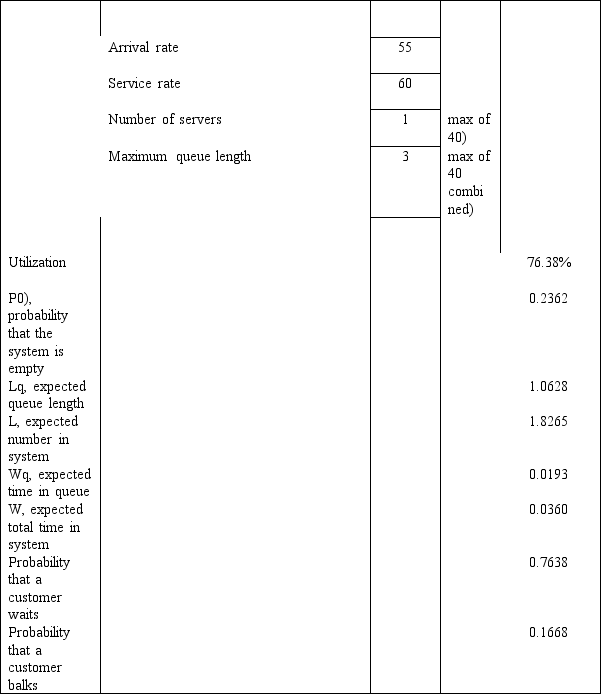
Refer to Exhibit 13.5.Based on this report how long does a computer user have to wait for his/her job to be completed?
The following questions refer to the information and output below.
A computer printer in a large administrative office has a printer buffer memory to store printing jobs)capacity of 3 jobs.If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later.There are so many users in this office that we can assume that there is an infinite calling population.Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print.Printing times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.5.Based on this report how long does a computer user have to wait for his/her job to be completed?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
66
Exhibit 13.
The following questions refer to the information and output below.
The university computer lab has 10 computers which are constantly being used by students.Users need help from the one lab assistant fairly often.Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer.The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.6.Based on this report how much time do students spend getting help before they can resume work on their computers?
The following questions refer to the information and output below.
The university computer lab has 10 computers which are constantly being used by students.Users need help from the one lab assistant fairly often.Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer.The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.6.Based on this report how much time do students spend getting help before they can resume work on their computers?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
67
The Kendall notation for a queuing system with Poisson arrivals,exponential service and 3 service providers is
A)M/M/3
B)M/G/1
C)G/G/3
D)G/G/1
A)M/M/3
B)M/G/1
C)G/G/3
D)G/G/1

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
68
Project 13.1 − Internet Sales,Inc.
Internet Sales,Inc.is establishing a new ordering system to handle its on-line sales.Customers arrive randomly at an average of one every minute.On average it takes 45 seconds to process a customer's order.The current system employs one network server to process orders.This server processes orders requests one at a time in the order received.The Internet Sales,Inc. ,Analysis Team has determined that customer orders arrive according to a Poisson process and the average time spent processing an order is exponentially distributed.
Internet Sales' management knows that offering prompt,reliable on-line service is critical to their continued success.Upgrading the current on-line ordering capacity will establish their image as a "cutting edge" on-line sales company.On the other hand,too much unused capacity is inefficient and will ultimately cause company profits to decline.
Recently,the management group established a goal of serving an on-line customer immediately,90% of the time.This means that 90% of the time a customer does not have to wait to place an order on-line after using the Internet Sales,Inc.web page.A heated discussion ensued over the current system's capability of meeting this goal.
Under the current system,a customer waits if the system is busy processing another order.Network server upgrades are available in increments of $5000.Each upgrade adds the capability to process an additional order in parallel.For example if two upgrades were purchased at a cost of $10,000,orders will be processed by three independent network servers each serving at an exponential rate of one order per 45 seconds.The Analysis Team was asked to consider the alternatives and recommend a course of action to the management group.What upgrade if any)will meet the service goal set by the management group? What are the cost and performance trade-offs?
Internet Sales,Inc.is establishing a new ordering system to handle its on-line sales.Customers arrive randomly at an average of one every minute.On average it takes 45 seconds to process a customer's order.The current system employs one network server to process orders.This server processes orders requests one at a time in the order received.The Internet Sales,Inc. ,Analysis Team has determined that customer orders arrive according to a Poisson process and the average time spent processing an order is exponentially distributed.
Internet Sales' management knows that offering prompt,reliable on-line service is critical to their continued success.Upgrading the current on-line ordering capacity will establish their image as a "cutting edge" on-line sales company.On the other hand,too much unused capacity is inefficient and will ultimately cause company profits to decline.
Recently,the management group established a goal of serving an on-line customer immediately,90% of the time.This means that 90% of the time a customer does not have to wait to place an order on-line after using the Internet Sales,Inc.web page.A heated discussion ensued over the current system's capability of meeting this goal.
Under the current system,a customer waits if the system is busy processing another order.Network server upgrades are available in increments of $5000.Each upgrade adds the capability to process an additional order in parallel.For example if two upgrades were purchased at a cost of $10,000,orders will be processed by three independent network servers each serving at an exponential rate of one order per 45 seconds.The Analysis Team was asked to consider the alternatives and recommend a course of action to the management group.What upgrade if any)will meet the service goal set by the management group? What are the cost and performance trade-offs?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
69
One reason to use queuing models in business is
A)to trade-off the cost of providing service and the cost of customer dissatisfaction
B)to maximize the number of service providers
C)to minimize the cost of providing service
D)all of the above
A)to trade-off the cost of providing service and the cost of customer dissatisfaction
B)to maximize the number of service providers
C)to minimize the cost of providing service
D)all of the above

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
70
Exhibit 13.
The following questions refer to the information and output below.
The university computer lab has 10 computers which are constantly being used by students.Users need help from the one lab assistant fairly often.Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer.The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.6.Based on this report what is the average number of students waiting to be helped?
The following questions refer to the information and output below.
The university computer lab has 10 computers which are constantly being used by students.Users need help from the one lab assistant fairly often.Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer.The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.6.Based on this report what is the average number of students waiting to be helped?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
71
Exhibit 13.
The following questions refer to the information and output below.
A tax accountant has found that the time to serve a customer has a mean of 30 minutes or 0.5 hours)and a standard deviation of 6 minutes or 0.1 hours).Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals.The following queuing analysis spreadsheet was developed from this information.
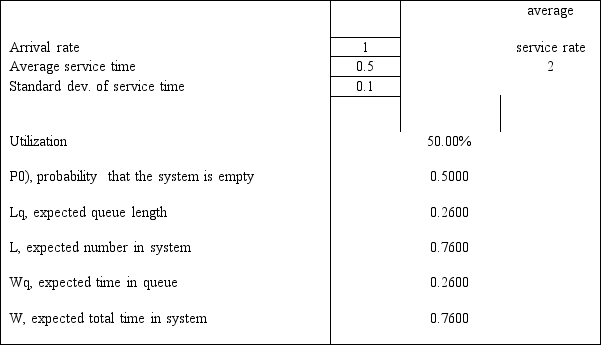
Refer to Exhibit 13.7.Based on this report what is the probability that a customer does not have to wait for assistance with his or her taxes?
The following questions refer to the information and output below.
A tax accountant has found that the time to serve a customer has a mean of 30 minutes or 0.5 hours)and a standard deviation of 6 minutes or 0.1 hours).Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.7.Based on this report what is the probability that a customer does not have to wait for assistance with his or her taxes?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
72
Exhibit 13.
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.Based on this report what is the average number of customers waiting for a checker?
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.Based on this report what is the average number of customers waiting for a checker?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
73
Exhibit 13.
The following questions refer to the information and output below.
A computer printer in a large administrative office has a printer buffer memory to store printing jobs)capacity of 3 jobs.If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later.There are so many users in this office that we can assume that there is an infinite calling population.Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print.Printing times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.5.Based on this report what is the probability that a computer user will be told to resubmit a print job at a later time?
The following questions refer to the information and output below.
A computer printer in a large administrative office has a printer buffer memory to store printing jobs)capacity of 3 jobs.If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later.There are so many users in this office that we can assume that there is an infinite calling population.Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print.Printing times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.5.Based on this report what is the probability that a computer user will be told to resubmit a print job at a later time?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
74
Exhibit 13.
The following questions refer to the information and output below.
A computer printer in a large administrative office has a printer buffer memory to store printing jobs)capacity of 3 jobs.If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later.There are so many users in this office that we can assume that there is an infinite calling population.Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print.Printing times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.5.What is the Kendall notation for this system?
The following questions refer to the information and output below.
A computer printer in a large administrative office has a printer buffer memory to store printing jobs)capacity of 3 jobs.If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later.There are so many users in this office that we can assume that there is an infinite calling population.Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print.Printing times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.5.What is the Kendall notation for this system?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
75
Exhibit 13.
The following questions refer to the information and output below.
A tax accountant has found that the time to serve a customer has a mean of 30 minutes or 0.5 hours)and a standard deviation of 6 minutes or 0.1 hours).Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.7.Based on this report what is the average number of customers waiting to be helped?
The following questions refer to the information and output below.
A tax accountant has found that the time to serve a customer has a mean of 30 minutes or 0.5 hours)and a standard deviation of 6 minutes or 0.1 hours).Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.7.Based on this report what is the average number of customers waiting to be helped?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
76
Exhibit 13.
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.Based on this report what percent of the time is a grocery clerk busy serving a customer?
The following questions refer to the information and output below.
A grocery store can serve an average of 360 customers per hour.The service times are exponentially distributed.The store has 4 checkout lines each of which serves 90 customers per hour.Customers arrive at the store at a Poisson rate of 240 customers per hour.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.4.Based on this report what percent of the time is a grocery clerk busy serving a customer?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
77
Exhibit 13.
The following questions refer to the information and output below.
A computer printer in a large administrative office has a printer buffer memory to store printing jobs)capacity of 3 jobs.If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later.There are so many users in this office that we can assume that there is an infinite calling population.Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print.Printing times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.5.Based on this report what is the average number of jobs waiting to be printed?
The following questions refer to the information and output below.
A computer printer in a large administrative office has a printer buffer memory to store printing jobs)capacity of 3 jobs.If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later.There are so many users in this office that we can assume that there is an infinite calling population.Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print.Printing times are exponentially distributed.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.5.Based on this report what is the average number of jobs waiting to be printed?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
78
Exhibit 13.
The following questions refer to the information and output below.
A tax accountant has found that the time to serve a customer has a mean of 30 minutes or 0.5 hours)and a standard deviation of 6 minutes or 0.1 hours).Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.7.What is the Kendall notation for this system?
The following questions refer to the information and output below.
A tax accountant has found that the time to serve a customer has a mean of 30 minutes or 0.5 hours)and a standard deviation of 6 minutes or 0.1 hours).Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.7.What is the Kendall notation for this system?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
79
Exhibit 13.
The following questions refer to the information and output below.
The university computer lab has 10 computers which are constantly being used by students.Users need help from the one lab assistant fairly often.Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer.The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.6.Based on this report what is the probability that a student will not get instantaneous help?
The following questions refer to the information and output below.
The university computer lab has 10 computers which are constantly being used by students.Users need help from the one lab assistant fairly often.Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer.The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.6.Based on this report what is the probability that a student will not get instantaneous help?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck
80
Exhibit 13.
The following questions refer to the information and output below.
A tax accountant has found that the time to serve a customer has a mean of 30 minutes or 0.5 hours)and a standard deviation of 6 minutes or 0.1 hours).Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.7.Based on this report how long does a customer spend at the tax accountant's office?
The following questions refer to the information and output below.
A tax accountant has found that the time to serve a customer has a mean of 30 minutes or 0.5 hours)and a standard deviation of 6 minutes or 0.1 hours).Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals.The following queuing analysis spreadsheet was developed from this information.

Refer to Exhibit 13.7.Based on this report how long does a customer spend at the tax accountant's office?

Unlock Deck
Unlock for access to all 87 flashcards in this deck.
Unlock Deck
k this deck



