Deck 15: Heaps and Priority Queues

Question 1

A binary search tree that is highly unbalanced is called a ________________ tree.

A) full
B) complete
C) degenerate
D) unsearchable
E) none of the above

Answer 1

C
Explanation: A binary search tree that is highly unbalanced is called a degenerate tree.

Question 2

In the worst case, a general binary search tree could require __________________ comparisons to find an element.

A) O(1)
B) O(n)
C) O(2ⁿ)
D) O(log₂ n)
E) none of the above

Answer 2

B
Explanation: If the elements of a binary search tree are inserted in increasing or decreasing order, then finding an element will require a number of comparisons that is linear in the number of elements.

Question 3

In a binary search tree, the elements in the right subtree of the root are always larger than the element stored at the root.

Answer 3

False
Explanation: The right subtree of the root may contain elements that are equal to the root.

Question 4

When removing an element from a binary search tree that has a single child, _____________________ will ensure that the resulting tree is still a binary search tree.

A) replacing it with its only child
B) replacing it with its inorder successor
C) simply deleting it
D) all of the above
E) neither a, b, nor c

Question 5

When removing an element from a binary search tree that has two children, _______________________ will ensure that the resulting tree is still a binary search tree.

A) replacing it with its only child
B) replacing it with its inorder successor
C) simply deleting it
D) all of the above
E) neither a, b, nor c

Question 6

In a binary search tree, the elements in the right subtree of the root are __________________ the root element.

A) greater than
B) less than
C) greater than or equal to
D) less than or equal to
E) equal to

Question 7

Finding an element in a binary search tree always requires O(log₂ n) comparisons.

Question 8

In a maxheap, the largest element in the structure is always ______________________ .

A) a leaf
B) an internal node
C) the root
D) the left child of the root
E) the right child of the root

Question 9

A binary search tree is always a full tree.

Question 10

A ____________________ is a complete binary tree in which each element is greater than or equal to both of its children.

A) binary search tree
B) stack
C) full tree
D) heap
E) none of the above

Question 11

When removing an element from a binary search tree that is a leaf, ______________ will ensure that the resulting tree is still a binary search tree.

A) replacing it with its only child
B) replacing it with its inorder successor
C) simply deleting it
D) all of the above
E) neither a, b, nor c

Question 12

A _____________________ is a tree whose elements are organized to facilitate finding a particular element when needed.

A) full tree
B) complete tree
C) binary tree
D) search tree
E) none of the above

Question 13

If a binary search tree becomes unbalanced after an element is added, it is sometimes possible to efficiently rebalance the tree by ___________________ .

A) using left and right rotations
B) selecting a leaf node to use as a new root
C) reconstructing the tree from scratch
D) all of the above
E) it is impossible to rebalance a tree efficiently

Question 14

When adding a new element to a binary search tree, the element is added as a(n) ______________.

A) internal node
B) subtree
C) leaf
D) root
E) none of the above

Question 15

Finding an element in a balanced binary search tree that contains n elements requires _____________________ comparisons.

A) O(1)
B) O(n)
C) O(2ⁿ)
D) O(log₂ n)
E) none of the above

Question 16

In a binary search tree, the elements in the left subtree of the root are __________________ the root element.

A) greater than
B) less than
C) greater than or equal to
D) less than or equal to
E) equal to

Question 17

In a binary search tree, a new element is always added as a leaf.

Question 18

When removing an element from a binary search tree, we must always ______________________.

A) make sure that the new tree is a binary search tree
B) build a new tree
C) find its inorder successor
D) remove all of its children
E) An element should never be removed from a binary search tree.

Question 19

In a balanced binary search tree, adding an element always requires approximately O(log₂ n) steps.

Question 20

Which of the following is always true when adding an element to a heap?

A) The new element will always be a leaf.
B) The new element will always be the root.
C) The new element will always be an internal node.
D) The new element will always have 2 children.
E) none of the above is always true

Question 21

Describe the steps involved in performing a right rotation on a node in a binary search tree.

Question 22

Suppose we have a class called BinaryTree that includes a find method. If we extend the class to create a BinarySearchTree class, should we override the find method or use it as is? Explain.

Question 23

What is the inorder successor of a node in a binary search tree?

Question 24

In a maxheap, the largest element is always the root.

Question 25

What is a heap?

Question 26

Left and right rotations can be used to rebalance an unbalanced binary search tree.

Question 27

Explain how to add an element to a binary search tree.

Question 28

Draw a binary search tree that results from inserting the following elements: 12, 16, 9, 1, 15, 13

Question 29

A heap sort sorts elements by constructing a heap out of them, and then removing them one at a time from the root.

Question 30

Explain how heap sort works.

Question 31

Describe how to find an element in a binary search tree. You may use English sentences or pseudocode.

Question 32

Consider the following binary search tree.
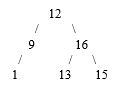What is the result of removing the following elements (in order): 13, 16, 12.

Question 33

The most efficient binary search trees are balanced.

Question 34

Whenever a new element is added to a maxheap, it always becomes the root.

Question 35

Does the find and add operations on a binary search tree always require at most O(log₂ n) comparisons? If so, why? If not, why not?

Question 36

What is special about the order in which the nodes are visited in an inorder traversal of a binary search tree.

Question 37

Explain the process of removing an element from a binary search tree.

Question 38

What is a binary search tree?

Question 39

Why is it important to keep a binary search tree balanced?

Question 40

Explain how an element is added to a heap.