Deck 21: What Is a Confidence Interval
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/43
Play
Full screen (f)
Deck 21: What Is a Confidence Interval
1
A recent survey reported that 52% of American adults surveyed consider the amount of federal income tax that they pay is too high (n = 1021, margin of error is ±3%). The poll was carried out by telephone, so people without phones are always excluded from the sample. Any errors in the final result due to excluding people without phones
A) are included in the announced margin of error.
B) are in addition to the announced margin of error.
C) can be ignored, because these people are not part of the population.
D) can be ignored, because this is a nonsampling error.
A) are included in the announced margin of error.
B) are in addition to the announced margin of error.
C) can be ignored, because these people are not part of the population.
D) can be ignored, because this is a nonsampling error.
are in addition to the announced margin of error.
2
The student newspaper at a college asks a simple random sample of 250 undergraduates, "Do you favor eliminating supplemental fees for lab courses?" In all, 150 of the 250 are in favor of eliminating such fees.
A 95% confidence interval for the population proportion p is
A) 150 ± 0.03.
B) 0.6 ± 0.03.
C) 150 ± 0.06.
D) 0.6 ± 0.06.
E) 1.67 ± 0.03.
A 95% confidence interval for the population proportion p is
A) 150 ± 0.03.
B) 0.6 ± 0.03.
C) 150 ± 0.06.
D) 0.6 ± 0.06.
E) 1.67 ± 0.03.
0.6 ± 0.06.
3
The student newspaper at a college asks a simple random sample of 250 undergraduates, "Do you favor eliminating supplemental fees for lab courses?" In all, 150 of the 250 are in favor of eliminating such fees.
To estimate p, you will use the proportion = 150/250 of your sample who favored eliminating supplemental fees for lab courses. The number is a
A) bias.
B) confidence level.
C) mean.
D) parameter.
E) statistic.
To estimate p, you will use the proportion = 150/250 of your sample who favored eliminating supplemental fees for lab courses. The number is a
A) bias.
B) confidence level.
C) mean.
D) parameter.
E) statistic.
statistic.
4
The phrase "95% confidence" in a confidence statement means that
A) the results are true for 95% of the population.
B) 95% of the population falls within the announced margin of error.
C) the probability is 0.95 that a randomly chosen individual's value falls within the announced margin of error.
D) the results were obtained using a method that gives correct answers in 95% of all samples.
A) the results are true for 95% of the population.
B) 95% of the population falls within the announced margin of error.
C) the probability is 0.95 that a randomly chosen individual's value falls within the announced margin of error.
D) the results were obtained using a method that gives correct answers in 95% of all samples.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
5
If we take a simple random sample of size n = 500 from a population of size 500,000, the variability of our estimate will be
A) less than the bias.
B) approximately the same as the variability for a sample of size n = 500 from a population of size 50,000,000.
C) plus or minus 0.1%.
D) much greater than the variability for a sample of size n = 500 from a population of size 50,000,000.
E) much less than the variability for a sample of size n = 500 from a population of size 50,000,000.
A) less than the bias.
B) approximately the same as the variability for a sample of size n = 500 from a population of size 50,000,000.
C) plus or minus 0.1%.
D) much greater than the variability for a sample of size n = 500 from a population of size 50,000,000.
E) much less than the variability for a sample of size n = 500 from a population of size 50,000,000.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
6
A recent Gallup Poll interviewed a random sample of 1523 adults. Of these, 868 bought a lottery ticket in the past year.
Suppose that in fact (unknown to Gallup) exactly 60% of all adults bought a lottery ticket in the past year. If Gallup took many simple random samples of 1523 people, the sample proportion who bought a ticket would vary from sample to sample. The sampling distribution would be close to normal with
A) mean 0.6 and standard deviation 0.00016.
B) mean 0.6 and standard deviation 0.0126.
C) mean 0.6 and standard deviation 0.4899.
D) mean 0.6 and standard deviation 0.0251.
Suppose that in fact (unknown to Gallup) exactly 60% of all adults bought a lottery ticket in the past year. If Gallup took many simple random samples of 1523 people, the sample proportion who bought a ticket would vary from sample to sample. The sampling distribution would be close to normal with
A) mean 0.6 and standard deviation 0.00016.
B) mean 0.6 and standard deviation 0.0126.
C) mean 0.6 and standard deviation 0.4899.
D) mean 0.6 and standard deviation 0.0251.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
7
Drawing conclusions about a population on the basis of data from a sample is called
A) statistical inference.
B) confidence interval.
C) sampling distribution.
D) populational statistics.
A) statistical inference.
B) confidence interval.
C) sampling distribution.
D) populational statistics.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
8
The confidence level is
A) another name for the margin of error.
B) the probability that the actual parameter value is in your computed interval.
C) a probability that says how often in many samples the method would produce an interval that contains the actual parameter value.
D) the standard deviation of the sampling distribution.
A) another name for the margin of error.
B) the probability that the actual parameter value is in your computed interval.
C) a probability that says how often in many samples the method would produce an interval that contains the actual parameter value.
D) the standard deviation of the sampling distribution.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
9
A surprising fact: only 56% of all teens use a password on their mobile device. If a poll chooses a simple random sample of 1000 teens and asks if they use a password on their mobile device, the percent who say "Yes" will vary if the sample is repeated. In fact, the percent "Yes" in many samples will follow a normal distribution with mean 56% and standard deviation 1.6%.
Although the result will vary if the poll is repeated, the distribution of results is centered at the truth about the population (56 percent). We call this desirable property of a simple random sample:
A) lack of bias.
B) low variability.
C) symmetry.
D) the confidence level.
Although the result will vary if the poll is repeated, the distribution of results is centered at the truth about the population (56 percent). We call this desirable property of a simple random sample:
A) lack of bias.
B) low variability.
C) symmetry.
D) the confidence level.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
10
A surprising fact: only 56% of all teens use a password on their mobile device. If a poll chooses a simple random sample of 1000 teens and asks if they use a password on their mobile device, the percent who say "Yes" will vary if the sample is repeated. In fact, the percent "Yes" in many samples will follow a normal distribution with mean 56% and standard deviation 1.6%.
Which of these ranges of outcomes contains 95 percent of all the results of a large number of polls of 1,000 teens?
A) 56 to 100 percent
B) 54.4 to 57.6 percent
C) 52.8 to 59.2 percent
D) 51.2 to 60.8 percent
Which of these ranges of outcomes contains 95 percent of all the results of a large number of polls of 1,000 teens?
A) 56 to 100 percent
B) 54.4 to 57.6 percent
C) 52.8 to 59.2 percent
D) 51.2 to 60.8 percent

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
11
A surprising fact: only 56% of all teens use a password on their mobile device. If a poll chooses a simple random sample of 1000 teens and asks if they use a password on their mobile device, the percent who say "Yes" will vary if the sample is repeated. In fact, the percent "Yes" in many samples will follow a normal distribution with mean 56% and standard deviation 1.6%.
The variation from sample to sample, when the poll is repeated, is described by the standard deviation (1.6 percent). We would like this variation to be small so that repeated polls give almost the same result. To reduce the standard deviation, we could:
A) use a simple random sample of size less than 1,000.
B) use a simple random sample of size greater than 1,000.
C) use a confidence level less than 95 percent.
D) use a confidence level greater than 95 percent.
E) use a simple random sample of size greater than 1,000, and use a confidence level less than 95 percent.
The variation from sample to sample, when the poll is repeated, is described by the standard deviation (1.6 percent). We would like this variation to be small so that repeated polls give almost the same result. To reduce the standard deviation, we could:
A) use a simple random sample of size less than 1,000.
B) use a simple random sample of size greater than 1,000.
C) use a confidence level less than 95 percent.
D) use a confidence level greater than 95 percent.
E) use a simple random sample of size greater than 1,000, and use a confidence level less than 95 percent.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
12
For a 95% confidence interval, a larger sample size will generally give
A) a least-squares line.
B) a larger margin of error.
C) less bias.
D) higher correlation.
E) a smaller margin of error.
A) a least-squares line.
B) a larger margin of error.
C) less bias.
D) higher correlation.
E) a smaller margin of error.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
13
A recent Gallup Poll interviewed a random sample of 1523 adults. Of these, 868 bought a lottery ticket in the past year.
The same Gallup Poll asked its 1523 adult respondents and also 501 teens (ages 13 to 17) whether they generally approved of legal gambling: 63% of adults and 52% of teens said yes. The margin of error for a 95% confidence statement about teens would be
A) greater than for adults, because the teen sample is smaller.
B) less than for adults, because the teen sample is smaller.
C) less than for adults, because there are fewer teens in the population.
D) the same as for adults, because they both come from the same sample survey.
E) Can't say, because it depends on what percent of each population was in the sample.
The same Gallup Poll asked its 1523 adult respondents and also 501 teens (ages 13 to 17) whether they generally approved of legal gambling: 63% of adults and 52% of teens said yes. The margin of error for a 95% confidence statement about teens would be
A) greater than for adults, because the teen sample is smaller.
B) less than for adults, because the teen sample is smaller.
C) less than for adults, because there are fewer teens in the population.
D) the same as for adults, because they both come from the same sample survey.
E) Can't say, because it depends on what percent of each population was in the sample.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
14
A recent Gallup Poll interviewed a random sample of 1523 adults. Of these, 868 bought a lottery ticket in the past year.
A 95% confidence interval for the proportion of all adults who bought a lottery ticket in the past year is (assume Gallup used a simple random sample)
A) 0.57 ± 0.00016.
B) 0.57 ± 0.00032.
C) 0.57 ± 0.013.
D) 0.57 ± 0.025.
E) 0.57 ± 0.03.
A 95% confidence interval for the proportion of all adults who bought a lottery ticket in the past year is (assume Gallup used a simple random sample)
A) 0.57 ± 0.00016.
B) 0.57 ± 0.00032.
C) 0.57 ± 0.013.
D) 0.57 ± 0.025.
E) 0.57 ± 0.03.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
15
You and a friend want to estimate the proportion of undergraduates at a college who favor eliminating evening exams. Your friend will choose a simple random sample of 250 students. If you choose a simple random sample of 1000 students, your sample proportion
A) will have the same mean and the same standard deviation.
B) will have smaller bias and the standard deviation will be 1/4 as large.
C) will have smaller bias and the standard deviation will be 1/2 as large.
D) will have the same mean and the standard deviation will be 1/4 as large.
E) will have the same mean and the standard deviation will be 1/2 as large.
A) will have the same mean and the same standard deviation.
B) will have smaller bias and the standard deviation will be 1/4 as large.
C) will have smaller bias and the standard deviation will be 1/2 as large.
D) will have the same mean and the standard deviation will be 1/4 as large.
E) will have the same mean and the standard deviation will be 1/2 as large.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
16
We observe = 0.4. If the standard deviation of the sampling distribution of is 0.03, what is the 95% confidence interval for p?
A) 0.37 to 0.43
B) 0.31 to 0.39
C) 0.34 to 0.46
D) 0.03 plus or minus 0.8
E) 99% accurate
A) 0.37 to 0.43
B) 0.31 to 0.39
C) 0.34 to 0.46
D) 0.03 plus or minus 0.8
E) 99% accurate

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
17
The student newspaper at a college asks a simple random sample of 250 undergraduates, "Do you favor eliminating supplemental fees for lab courses?" In all, 150 of the 250 are in favor of eliminating such fees.
Suppose that (unknown to you) 55% of all undergraduates favor eliminating supplemental fees for lab courses. If you took a very large number of simple random samples of size n = 250 from this population, the sampling distribution of the sample proportion p would be approximately normal with
A) mean 0.55 and standard deviation 0.015.
B) mean 0.60 and standard deviation 0.06.
C) mean 0.55 and standard deviation 0.06.
D) mean 0.60 and standard deviation 0.03.
E) mean 0.55 and standard deviation 0.03.
Suppose that (unknown to you) 55% of all undergraduates favor eliminating supplemental fees for lab courses. If you took a very large number of simple random samples of size n = 250 from this population, the sampling distribution of the sample proportion p would be approximately normal with
A) mean 0.55 and standard deviation 0.015.
B) mean 0.60 and standard deviation 0.06.
C) mean 0.55 and standard deviation 0.06.
D) mean 0.60 and standard deviation 0.03.
E) mean 0.55 and standard deviation 0.03.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
18
The student newspaper at a college asks a simple random sample of 250 undergraduates, "Do you favor eliminating supplemental fees for lab courses?" In all, 150 of the 250 are in favor of eliminating such fees.
The ___________ you want to estimate is the proportion p of all undergraduates who favor eliminating the supplemental fees for lab courses.
A) bias
B) confidence level
C) mean
D) parameter
E) statistic
The ___________ you want to estimate is the proportion p of all undergraduates who favor eliminating the supplemental fees for lab courses.
A) bias
B) confidence level
C) mean
D) parameter
E) statistic

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
19
The margin of error for a 95% confidence interval is 2.8. If we decrease the confidence level to 90%, the margin of error will be
A) biased.
B) 99%.
C) 2.8.
D) smaller than 2.8.
E) larger than 2.8.
A) biased.
B) 99%.
C) 2.8.
D) smaller than 2.8.
E) larger than 2.8.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
20
The student newspaper at a college asks a simple random sample of 250 undergraduates, "Do you favor eliminating supplemental fees for lab courses?" In all, 150 of the 250 are in favor of eliminating such fees.
A 90% confidence interval based on this same sample would have
A) the same center and a larger margin of error.
B) the same center and a smaller margin of error.
C) a larger margin of error and probably a different center.
D) a smaller margin of error and probably a different center.
E) the same center, but the margin of error changes randomly.
A 90% confidence interval based on this same sample would have
A) the same center and a larger margin of error.
B) the same center and a smaller margin of error.
C) a larger margin of error and probably a different center.
D) a smaller margin of error and probably a different center.
E) the same center, but the margin of error changes randomly.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
21
The name for the pattern of values that a statistic takes when we sample repeatedly from the same population is
A) the bias of the statistic.
B) the sampling distribution of the statistic.
C) the scale of measurement of the statistic.
D) the variability of the statistic.
E) the sampling error.
A) the bias of the statistic.
B) the sampling distribution of the statistic.
C) the scale of measurement of the statistic.
D) the variability of the statistic.
E) the sampling error.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
22
A member of the city government thinks that 90 percent confidence isn't enough. He wants to be 99 percent confident. How would the margin of error of a 99 percent confidence interval compare with the 90 percent interval found for the same sample?
A) It would be smaller because it omits only 1 percent of the possible samples instead of 10 percent.
B) It would be the same because the sample is the same.
C) It would be larger because higher confidence requires a larger margin of error.
D) It is impossible to tell because the margin of error is random.
E) It is impossible to tell unless a census is taken.
A) It would be smaller because it omits only 1 percent of the possible samples instead of 10 percent.
B) It would be the same because the sample is the same.
C) It would be larger because higher confidence requires a larger margin of error.
D) It is impossible to tell because the margin of error is random.
E) It is impossible to tell unless a census is taken.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
23
You choose a simple random sample of 2000 women over 18 years of age from the New York City metropolitan area; 623 of them are single. A 90% confidence interval for the proportion of all adult women in the New York area who are single is (approximately)
A) 0.3115 ± 0.017.
B) 0.623 ± 0.017.
C) 0.3115 ± 0.0207.
D) 0.623 ± 0.0207.
E) 0.3115 ± 0.0267.
A) 0.3115 ± 0.017.
B) 0.623 ± 0.017.
C) 0.3115 ± 0.0207.
D) 0.623 ± 0.0207.
E) 0.3115 ± 0.0267.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
24
A November 2015 poll of size n = 1021 had a sample proportion = 0.86 disapproving of Congress. If this is regarded as a simple random sample, then a 95 percent confidence interval for the proportion p of all adults who disapprove of Congress is closest to:
A) 0.86 ± 0.000231.
B) 0.86 ± 0.0105.
C) 0.86 ± 0.021.
D) 0.86 ± 0.03.
A) 0.86 ± 0.000231.
B) 0.86 ± 0.0105.
C) 0.86 ± 0.021.
D) 0.86 ± 0.03.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
25
In a simple random sample of 100 women from Richmond, Virginia, the average amount of money that these women spent per visit at their hair salons is $32.43. The standard deviation from this sample is $7.84.
Which of these is a correct 95% confidence statement for the interval in the previous question?
A) We are 95% confident that the mean amount of money that all women in Richmond spend per visit at their hair salons is within the computed interval.
B) We are 95% confident that the mean amount of money that all women in the sample spend per visit at their hair salons is within the computed interval.
C) The mean amount of money that 95% of women in Richmond spend per visit at their hair salons is within the computed interval.
D) The mean amount of money that 95% of women in the sample spend per visit at their hair salons is within the computed interval.
Which of these is a correct 95% confidence statement for the interval in the previous question?
A) We are 95% confident that the mean amount of money that all women in Richmond spend per visit at their hair salons is within the computed interval.
B) We are 95% confident that the mean amount of money that all women in the sample spend per visit at their hair salons is within the computed interval.
C) The mean amount of money that 95% of women in Richmond spend per visit at their hair salons is within the computed interval.
D) The mean amount of money that 95% of women in the sample spend per visit at their hair salons is within the computed interval.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
26
A poll of 1,006 American adults found that 30 percent believe the government should do "a great deal" about global warming. Taking the poll's sample to be a simple random sample of all American adults, which of these is a correct 95 percent confidence statement?
A) With 95 percent confidence (but not certainty), the percent of the sample who believe the government should do "a great deal" about global warming is between 28.6 and 31.4 percent.
B) With 95 percent confidence (but not certainty), the percent of the sample who believe the government should do "a great deal" about global warming is between 27.2 and 32.8 percent.
C) With 95 percent confidence, the percent of all American adults who believe the government should do "a great deal" about global warming is between 28.6 and 31.4 percent.
D) With 95 percent confidence, the percent of all American adults who believe the government should do "a great deal" about global warming is between 27.2 and 32.8 percent.
A) With 95 percent confidence (but not certainty), the percent of the sample who believe the government should do "a great deal" about global warming is between 28.6 and 31.4 percent.
B) With 95 percent confidence (but not certainty), the percent of the sample who believe the government should do "a great deal" about global warming is between 27.2 and 32.8 percent.
C) With 95 percent confidence, the percent of all American adults who believe the government should do "a great deal" about global warming is between 28.6 and 31.4 percent.
D) With 95 percent confidence, the percent of all American adults who believe the government should do "a great deal" about global warming is between 27.2 and 32.8 percent.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
27
If the 1,017 people in the previous question had called a 900 number to give their opinions, how would this have affected the response?
A) Not at all, because the width of the confidence interval depends only on the sample size, and not on the population size.
B) Not at all, because the width of the confidence interval depends only on the sample size, and not on how the sample was obtained.
C) It would be wider because voluntary response polls have a bigger margin of error than simple random samples.
D) It would be narrower because voluntary response polls are less variable than simple random samples.
E) A confidence interval makes no sense for a voluntary response sample.
A) Not at all, because the width of the confidence interval depends only on the sample size, and not on the population size.
B) Not at all, because the width of the confidence interval depends only on the sample size, and not on how the sample was obtained.
C) It would be wider because voluntary response polls have a bigger margin of error than simple random samples.
D) It would be narrower because voluntary response polls are less variable than simple random samples.
E) A confidence interval makes no sense for a voluntary response sample.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
28
A sample survey finds that 72 percent of a sample of 1,017 adults in Kentucky wanted the recently elected governor to retain the health-insurance plan mandated by the Affordable Care Act. If that sample were a simple random sample from the population of all Ohio adults, what would be the 99 percent confidence interval for the percent of all Kentucky adults who feel that way?
A) 66 to 74 percent
B) 67 to 75 percent
C) 68 to 76 percent
D) 67 to 77 percent
E) 66 to 78 percent
A) 66 to 74 percent
B) 67 to 75 percent
C) 68 to 76 percent
D) 67 to 77 percent
E) 66 to 78 percent

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
29
The weights for a population of North American raccoons have a bell-shaped frequency curve with a mean of about 12 pounds and a standard deviation of about 2.5 pounds.
About 95% of the weights for individual raccoons in this population fall between what two values?
A) 11.75 and 12.25
B) 11.5 and 12.5
C) 2.5 and 12
D) 7 and 17
E) 9.5 and 14.5
About 95% of the weights for individual raccoons in this population fall between what two values?
A) 11.75 and 12.25
B) 11.5 and 12.5
C) 2.5 and 12
D) 7 and 17
E) 9.5 and 14.5

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
30
An April 2016 opinion poll asked 1,190 adults what they felt the most pressing problem facing the country was, and 476 replied that economic problems in general were the most pressing problem. The sample should be considered as a simple random sample from the population of all adults. Based on the results of this poll, which of these is an approximately 95 percent confidence interval for the proportion of all adults who would reply that economic problems are the most pressing of those facing the country?
A) 0.40 ± 0.0004
B) 0.40 ± 0.014
C) 0.40 ± 0.0186
D) 0.40 ± 0.0285
E) 0.40 ± 0.037
A) 0.40 ± 0.0004
B) 0.40 ± 0.014
C) 0.40 ± 0.0186
D) 0.40 ± 0.0285
E) 0.40 ± 0.037

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
31
The weights for a population of North American raccoons have a bell-shaped frequency curve with a mean of about 12 pounds and a standard deviation of about 2.5 pounds.
About 95% of the mean weights from samples of size 100 raccoons from this population fall between what two values?
A) 11.75 and 12.25
B) 11.5 and 12.5
C) 2.5 and 12
D) 7 and 17
E) 9.5 and 14.5
About 95% of the mean weights from samples of size 100 raccoons from this population fall between what two values?
A) 11.75 and 12.25
B) 11.5 and 12.5
C) 2.5 and 12
D) 7 and 17
E) 9.5 and 14.5

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
32
An ad for ARCO graphite motor oil says (really): "Based on a 95% confidence level, our tests achieved between 1% and 8.7% mileage improvement" as compared with a conventional motor oil. What does the phrase "95% confidence level" mean here?
A) ARCO graphite beats 95% of conventional motor oils.
B) The interval from 1% to 8.7% covers 95% of the mileage improvements observed in the tests.
C) The tests included 95% of all oil brands on the market.
D) The estimate that mileage improves somewhere between 1% and 8.7% came from a method that would catch the true improvement in 95% of all similar tests.
E) A mistake has been made, because 95% + 8.7% is more than 100%.
A) ARCO graphite beats 95% of conventional motor oils.
B) The interval from 1% to 8.7% covers 95% of the mileage improvements observed in the tests.
C) The tests included 95% of all oil brands on the market.
D) The estimate that mileage improves somewhere between 1% and 8.7% came from a method that would catch the true improvement in 95% of all similar tests.
E) A mistake has been made, because 95% + 8.7% is more than 100%.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
33
A researcher chooses a simple random sample of 100 Lexington, Kentucky, residents and finds that 20 of them have put in a reservation for a Tesla Model 3. A 95 percent confidence interval for the proportion of all Lexington, Kentucky, residents who have put in a reservation for that car is (approximately):
A) 20 ± 3.
B) 0.10 ± 0.04.
C) 0.95 ± 0.20.
D) 20 ± 6.
E) 0.20 ± 0.08.
A) 20 ± 3.
B) 0.10 ± 0.04.
C) 0.95 ± 0.20.
D) 20 ± 6.
E) 0.20 ± 0.08.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
34
In a simple random sample of 100 women from Richmond, Virginia, the average amount of money that these women spent per visit at their hair salons is $32.43. The standard deviation from this sample is $7.84.
Suppose that a simple random sample of 100 men in Richmond were asked how much money they spent per visit at the barbershop. The responses resulted in a mean of $21.43 and a standard deviation of $7.84. The margin of error for a 95% confidence interval for the mean amount of money that all men in Richmond spend per visit at their barbershops would be
A) larger than for women, because the men's mean was smaller.
B) smaller than for women, because the men's mean was smaller.
C) the same as for women.
D) invalid because hair salons and barbershops charge for different services.
Suppose that a simple random sample of 100 men in Richmond were asked how much money they spent per visit at the barbershop. The responses resulted in a mean of $21.43 and a standard deviation of $7.84. The margin of error for a 95% confidence interval for the mean amount of money that all men in Richmond spend per visit at their barbershops would be
A) larger than for women, because the men's mean was smaller.
B) smaller than for women, because the men's mean was smaller.
C) the same as for women.
D) invalid because hair salons and barbershops charge for different services.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
35
In a simple random sample of 144 households in a city in Kentucky, the average number of children in these households was 1.12 children. The standard deviation from this sample was 2.40 children. A 90 percent confidence interval for the mean number of children in all households in this city is:
A) 2.40 ± 0.2.
B) 1.12 ± 0.2.
C) 1.12 ± 2.40.
D) 1.12 ± 0.328.
E) It is impossible to tell without a census.
A) 2.40 ± 0.2.
B) 1.12 ± 0.2.
C) 1.12 ± 2.40.
D) 1.12 ± 0.328.
E) It is impossible to tell without a census.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
36
A poll of 1,190 adults found that 476 felt economic problems were the most pressing of those facing the country. The sample proportion who expressed that opinion is:
A) unknown, because only information on 1,190 people is known.
B) unknown until the confidence level is decided.
C) 2.50.
D) 0.40.
E) 0.60.
A) unknown, because only information on 1,190 people is known.
B) unknown until the confidence level is decided.
C) 2.50.
D) 0.40.
E) 0.60.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
37
Another member of the city government is satisfied with 90% confidence, but she wants a smaller margin of error. How can we get a smaller margin of error, still with 90% confidence?
A) Take a larger sample, because larger samples result in smaller margins of error.
B) Take a smaller sample, because smaller samples result in smaller margins of error.
C) Take another sample of the same size and you might be lucky and get a much smaller margin of error.
D) Take a sample of adults from a neighborhood in the county instead of from the entire county. Then, the population will be smaller which will give a smaller margin of error.
E) Carry out a call-in poll to get a voluntary response sample. Voluntary response samples have no margin of error.
A) Take a larger sample, because larger samples result in smaller margins of error.
B) Take a smaller sample, because smaller samples result in smaller margins of error.
C) Take another sample of the same size and you might be lucky and get a much smaller margin of error.
D) Take a sample of adults from a neighborhood in the county instead of from the entire county. Then, the population will be smaller which will give a smaller margin of error.
E) Carry out a call-in poll to get a voluntary response sample. Voluntary response samples have no margin of error.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
38
In a simple random sample of 100 women from Richmond, Virginia, the average amount of money that these women spent per visit at their hair salons is $32.43. The standard deviation from this sample is $7.84.
Which of these is an approximate 95% confidence interval for the mean amount of money that all women in Richmond spend per visit at their hair salons?
A) $32.43 ± $0.784
B) $32.43 ± $1.568
C) $32.43 ± $7.84
D) $7.84 ± $3.243
E) $7.84 ± $6.486
Which of these is an approximate 95% confidence interval for the mean amount of money that all women in Richmond spend per visit at their hair salons?
A) $32.43 ± $0.784
B) $32.43 ± $1.568
C) $32.43 ± $7.84
D) $7.84 ± $3.243
E) $7.84 ± $6.486

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
39
A recent survey of 54,000 randomly selected U.S. adults studied the religious affiliation of Americans. The survey interviewed 645 people in Oregon. Suppose that this is a simple random sample of adult residents of Oregon. Of these 645 people, 116 said they claimed no religious identity. A 95 percent confidence interval for the proportion of all residents of Oregon who claim no religious identity is closest to:
A) 0.16 to 0.20.
B) 0.15 to 0.21.
C) 0.14 to 0.22.
D) 0.13 to 0.23.
A) 0.16 to 0.20.
B) 0.15 to 0.21.
C) 0.14 to 0.22.
D) 0.13 to 0.23.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
40
Most people can roll their tongues, but many people can't. Whether or not a person can roll his tongue is genetically determined. Suppose we are interested in determining what percentage of students can roll their tongues. We get a simple random sample of 400 students and find that 317 can roll their tongues. The margin of error for a 95% confidence interval for the true percentage of tongue-rollers among students is closest to
A) 0.04%.
B) 2.0%.
C) 3.0%.
D) 4.0%.
E) 20.75%.
A) 0.04%.
B) 2.0%.
C) 3.0%.
D) 4.0%.
E) 20.75%.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
41
The formula for a 95% confidence interval for a population proportion is given by 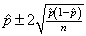
) The entire "plus or minus part" of this confidence interval is also called the
A) standard deviation.
B) margin of error.
C) confidence level.
D) sampling distribution.
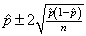
) The entire "plus or minus part" of this confidence interval is also called the
A) standard deviation.
B) margin of error.
C) confidence level.
D) sampling distribution.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
42
The _______________ says that, as we take more and more observations at random from any population, the distribution of the mean of these observations eventually gets close to a Normal distribution.
A) Statistical inference
B) Normal mean theorem
C) Law of large numbers
D) Central limit theorem
A) Statistical inference
B) Normal mean theorem
C) Law of large numbers
D) Central limit theorem

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck
43
In a simple random sample of 75 working adults in a city in Virginia, the average commute time for these workers was 23.65 minutes. The standard deviation from this sample was 18.50 minutes. A 95% confidence interval for the mean commute time for all adult workers in this city is approximately
A) 18.50 ± 2.73.
B) 18.50 ± 5.46.
C) 23.65 ± 4.187.
D) 23.65 ± 2.136.
A) 18.50 ± 2.73.
B) 18.50 ± 5.46.
C) 23.65 ± 4.187.
D) 23.65 ± 2.136.

Unlock Deck
Unlock for access to all 43 flashcards in this deck.
Unlock Deck
k this deck



