Deck 9: Analytical Trigonometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 9: Analytical Trigonometry
1
Convert the expression into a product. Simplify where possible. (Hint: Use the identity .)
A)
B) 1/2
C) 1
D) 0
E)
A)
B) 1/2
C) 1
D) 0
E)
0
2
Use the addition formulas for sine and cosine to simplify the expression.
A)
B) 1/2
C) 0
D) 1
E)
A)
B) 1/2
C) 0
D) 1
E)
1/2
3
Use a product-to-sum formula to convert the expression to a sum or difference. Simplify where possible.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Refer to the triangle and compute . 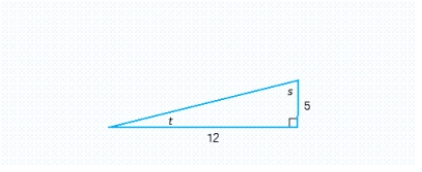
A) 1/5
B)
C)
D) 1/8
E)

A) 1/5
B)
C)
D) 1/8
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
Compute and using the data below.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
Use the given information to compute . and
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
Use the given information to compute . and
A)
B)
C)
D) 4/15
E)
A)
B)
C)
D) 4/15
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
Determine all of the solutions in the interval .
A) , and
B) , and
C) , and
D) , and
E) , and
F)
G) no solution.
A) , and
B) , and
C) , and
D) , and
E) , and
F)
G) no solution.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
Find the right side of the identity.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
10
Is a solution of ?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
Refer to the triangle and compute . 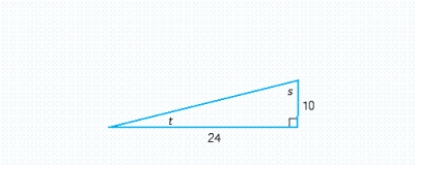
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
Use a product-to-sum formula to convert the expression to a sum or difference. Simplify where possible.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13
Use the addition formulas for tangent to simplify the expression.
A)
B)
C)
D)
E) 1
A)
B)
C)
D)
E) 1

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
Use a product-to-sum formula to convert the expression to a sum or difference. Simplify where possible.
A) 0
B) -1/4
C) -1/2
D) 1/4
E) 1/2
A) 0
B) -1/4
C) -1/2
D) 1/4
E) 1/2

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
Use the following information to evaluate the expression.
A)
B)
C) 8/7
D) -1/3
E) -1/5
A)
B)
C) 8/7
D) -1/3
E) -1/5

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
Use a product-to-sum formula to convert the expression to a sum or difference. Simplify where possible.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
Use the addition formulas for sine and cosine to simplify the expression.
A)
B)
C)
D) 0
E) 3
A)
B)
C)
D) 0
E) 3

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
Use the given information to compute and . and
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19
Use the formula for to compute the exact value of .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20
Compute and using the data below.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate the quantity that is defined, but do not use a calculator or tables.
A) -π/4
B) -π/3
C) -π/2
D) π/4
E) -π/6
A) -π/4
B) -π/3
C) -π/2
D) π/4
E) -π/6

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate the quantity without using a calculator or tables.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate the given quantity, but do not use a calculator or table.
A) π
B)
C) 0
D)
E)
A) π
B)
C) 0
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the quantity without using a calculator or tables.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate the quantity without using a calculator or tables.
A) 1/2
B)
C)
D) -1/2
E)
A) 1/2
B)
C)
D) -1/2
E)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck



