Deck 9: One-Sample Tests of Hypothesis

Question 1

i. Two examples of a hypothesis are: 1) mean monthly income from all sources for senior citizens is $841 and
2) twenty percent of juvenile offenders ultimately are caught and sentenced to prison.
ii. Hypothesis testing is a procedure based on sample evidence and probability theory to decide whether the hypothesis is a reasonable statement.
iii. Since there is more variability in sample means computed from smaller samples, we have more confidence in the resulting estimates and are less apt to reject null hypothesis.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Answer 1

(i) and (ii) are correct statements but not (iii).

Question 2

Which of the following does NOT hold true for the t distribution?

A) Confidence intervals will be wider than for large samples.
B) The region of acceptance will be larger than for large samples.
C) A larger computed t value will be needed to reject the null hypothesis than for large samples using z.
D) There is only one t distribution.

Answer 2

There is only one t distribution.

Question 3

The null hypothesis makes a claim about what value?

A) Population parameter
B) Sample statistic
C) Sample mean
D) Type II error

Answer 3

Population parameter

Question 4

i. Two types of possible errors always exist when testing hypotheses-a Type I error, in which the null hypothesis is rejected when it should not have been rejected, and a Type II error in which the null hypothesis is not rejected when it should have been rejected. ii. A test statistic is a value determined from sample information collected to test the null hypothesis.
iii. The region or area of rejection defines the location of all those values that are so large or so small that the probability of their occurrence under a true null hypothesis is rather remote.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 5

i. If we do not reject the null hypothesis based on sample evidence, we have proven beyond doubt that the null hypothesis is true. ii. A test statistic is a value determined from sample information collected to test the null hypothesis.
iii. The region or area of rejection defines the location of all those values that are so large or so small that the probability of their occurrence under a true null hypothesis is rather remote.

A) (ii) and (iii) are correct statements but not (i).
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 6

i. Two examples of a hypothesis are: 1) mean monthly income from all sources for senior citizens is $841 and 2) twenty percent of juvenile offenders ultimately are caught and sentenced to prison. ii. Hypothesis testing is a procedure based on sample evidence and probability theory to decide whether the hypothesis is a reasonable statement.
iii. We call a statement about the value of a population parameter a hypothesis.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 7

i. To prevent bias, the level of significance is selected before setting up the decision rule and sampling the population. ii. The fifth and final step in testing a hypothesis is taking a sample and, based on the decision rule, deciding if the null hypothesis should be rejected.
iii. When the null hypothesis is not rejected, the conclusion is that our sample data does not allow us to reject the null hypothesis.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 8

i. An alternate hypothesis is a statement about a population parameter that is accepted when the null hypothesis is rejected. ii. The level of significance is the risk we assume of rejecting the null hypothesis when it is actually true.
iii. The researcher must decide on the level of significance before formulating a decision rule and collecting sample data.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 9

i. Two examples of a hypothesis are: 1) mean monthly income from all sources for senior citizens is $841 and
2) twenty percent of juvenile offenders ultimately are caught and sentenced to prison.
ii. Since there is more variability in sample means computed from smaller samples, we have more confidence in the resulting estimates and are less apt to reject null hypothesis.
iii. We call a statement about the value of a population parameter a hypothesis.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 10

i. Two types of possible errors always exist when testing hypotheses-a Type I error, in which the null hypothesis is rejected when it should not have been rejected, and a Type II error in which the null hypothesis is not rejected when it should have been rejected. ii. A test statistic is a value determined from sample information collected to test the null hypothesis.
iii. If we do not reject the null hypothesis based on sample evidence, we have proven beyond doubt that the null hypothesis is true.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 11

It is claimed that in a bushel of peaches less than ten percent are defective. A sample of 400 peaches is examined and 50 are found to be defective. If $\alpha$ = 0.025, what will be the decision?

A) Fail to reject the null and conclude the defects are not greater than 10%
B) Reject the null and conclude the defects are not greater than 10%
C) Reject the null and conclude the defects are greater than 10%
D) Fail to reject the null and conclude the defects are not less than 10%

Question 12

i. The level of significance is the risk we assume of rejecting the null hypothesis when it is actually true. ii. There is only one level of significance that is applied to all studies involving sampling.
iii. The researcher must decide on the level of significance before formulating a decision rule and collecting sample data.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 13

i. The first step in testing a hypothesis is to state the decision rule. ii. To prevent bias, the level of significance is selected before setting up the decision rule and sampling the population.
iii. The fifth and final step in testing a hypothesis is taking a sample and, based on the decision rule, deciding if the null hypothesis should be rejected.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (ii) and (iii) are correct statements but not (i).

Question 14

i. To set up a decision rule, the sampling distribution is divided into two regions-a region of non-rejection and a region where the null hypothesis is rejected. ii. A test statistic is a value determined from sample information collected to test the null hypothesis.
iii. If the null hypothesis is true and the researchers do not reject it, then a correct decision has been made.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 15

i. The fifth and final step in testing a hypothesis is taking a sample and, based on the decision rule, deciding if the null hypothesis should be rejected. ii. When the null hypothesis is not rejected, the conclusion is that our sample data does not allow us to reject the null hypothesis.
iii. The level of significance is selected after setting up a decision rule and sampling the population.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 16

i. An alternate hypothesis is a statement about a population parameter that is accepted when the null hypothesis is rejected. ii. The level of significance is the risk we assume of rejecting the null hypothesis when it is actually true.
iii. There is only one level of significance that is applied to all studies involving sampling.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 17

i. To prevent bias, the level of significance is selected before setting up the decision rule and sampling the population. ii. The level of significance is the probability that a true hypothesis is rejected.
iii. If the critical values of the test statistic z are $\pm$ 1.96, they are the dividing points between the areas of rejection and non-rejection.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (ii) and (iii) are correct statements but not (i).

Question 18

i. Two examples of a hypothesis are: 1) mean monthly income from all sources for senior citizens is $841 and
2) twenty percent of juvenile offenders ultimately are caught and sentenced to prison.
ii. Since there is more variability in sample means computed from smaller samples, we have more confidence in the resulting estimates and are less apt to reject null hypothesis.
iii. The test statistic for a problem where the population standard deviation is unknown is the Student's t distribution.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 19

The average cost of tuition, room and board at community colleges is reported to be $11,500 per year, but a financial administrator believes that the average cost is higher. A study conducted using 150 community colleges showed that the average cost per year is $12,000 with a standard deviation of $1,200. Let $\alpha$ = 0.05. What are the null and alternative hypotheses for this study?

A) Null: $\mu$ $\le$ $12,000; alternative: $\mu$ > $12,000
B) Null: $\mu$ $\le$ $12,000; alternative: $\mu$ < $12,000
C) Null: $\mu$ $\le$ $11,500; alternative: $\mu$ > $11,500
D) Null: $\mu$ $\le$ $11,500; alternative: $\mu$ < $11,500

Question 20

i. Two examples of a hypothesis are: 1) mean monthly income from all sources for senior citizens is $841 and 2) twenty percent of juvenile offenders ultimately are caught and sentenced to prison. ii. Hypothesis testing is a procedure based on sample evidence and probability theory to decide whether the hypothesis is a reasonable statement.
iii. The test statistic for a problem involving an unknown population standard deviation is the Student's t distribution.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (i) and (ii) are correct statements but not (iii).
E) (i), (ii), and (iii) are all false statements.

Question 21

What are the two rejection areas in using a two-tailed test and the 0.01 level of significance when the population standard deviation is known?

A) Above 1.96 and below -1.96
B) Above 1.65 and below -1.65
C) Above 2.58 and below -2.58
D) Above 1.00 and below -1.00

Question 22

From past records it is known that the average life of a battery used in a digital clock is 305 days. The battery life is normally distributed. The battery was recently modified to last longer. A sample of 20 of the modified batteries was tested. It was discovered that the mean life was 311 days and the sample standard deviation was 12 days. We want to test at the 0.05 level of significance whether the modification increases the life of the battery. What is our decision rule?

A) Do not reject the null hypothesis if computed t is 1.96 or greater
B) Reject the null hypothesis if computed t is less than 1.96
C) Do not reject the null hypothesis if computed t is 1.729 or greater
D) Reject the null hypothesis if computed t is 2.086 or greater
E) Reject the null hypothesis if the computed t is 1.729 or greater

Question 23

i. If the null hypothesis is $\mu$ $\ge$ 200 and the alternate hypothesis states that $\mu$ is less than 200, then, a two-tail test is being conducted. ii. For a one-tailed test of hypothesis, the area of rejection is only in one tail of the curve.
iii. As the sample size increases, the curve of the t-distribution approaches the standard normal distribution

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 24

A nationwide survey of college students was conducted and found that students spend two hours per class hour studying. A professor at your school wants to determine whether the time students spend at your school is significantly different from the two hours. A random sample of fifteen statistics students is carried out and the findings indicate an average of 1.75 hours with a standard deviation of 0.24 hours. Test at the 5% level of significance.

A) The critical value of t is -4.03. The calculated value of t is $\pm$ 2.145.
B) The critical value of t is $\pm$ 2.145. The calculated value of t is -4.03.
C) The critical value of t is 1.761. The calculated value of t is -4.03.
D) The critical value of t is $\pm$ 1.761. The calculated value of t is -1.041.
E) The t-test should not be used. Rather, use the z-test.

Question 25

If the alternative hypothesis states that $\mu$ > 6,700, what is the rejection region for the hypothesis test?

A) Both tails
B) Lower tail
C) Upper tail
D) Center

Question 26

What is the critical value for a one-tailed hypothesis test in which a null hypothesis is tested at the 5% level of significance based on a sample size of 25 and an unknown population standard deviation?

A) 1.708
B) 1.711
C) 2.060
D) 2.064

Question 27

The mean gross annual incomes of certified tack welders are normally distributed with the mean of $50,000 and a standard deviation of $4,000. The ship building association wishes to find out whether their tack welders earn more or less than $50,000 annually. The alternate hypothesis is that the mean is not $50,000. Which of the following is the alternate hypothesis?

A) p $\neq$ $50,000
B) $\mu$ $\neq$ $50,000
C) $\mu$ < $50,000
D) $\mu$ = $50,000
E) p = $50,000

Question 28

What are the critical z-values for a two-tailed hypothesis test if $\alpha$ = 0.01?

A) $\pm$ 1.96
B) $\pm$ 2.33
C) $\pm$ 2.58
D) $\pm$ 1.65

Question 29

A random sample of size 15 is selected from a normal population. The population standard deviation is unknown. Assume that a two-tailed test at the 0.10 significance level is to be used. For what value of t will the null hypothesis be rejected?

A) To the left of-1.282 or to the right of 1.282
B) To the left of-1.345 or to the right of 1.345
C) To the left of-1.761 or to the right of 1.761
D) To the left of-1.645 or to the right of 1.645

Question 30

A nationwide survey of college students was conducted and found that students spend two hours per class hour studying. A professor at your school wants to determine whether the time students spend at your school is significantly different from the two hours. A random sample of fifteen statistics students is carried out and the findings indicate an average of 1.75 hours with a standard deviation of 0.24 hours.

A) H0 is $\mu$ $\neq$ 2. H1 is $\mu$ = 2.
B) H0 is $\mu$ = 2. H1 is $\mu$ $\neq$ 2.
C) H0 is $\mu$ = 2. H1 is $\mu$ > 2.
D) H0 is $\mu$ = 2. H1 is $\mu$ < 2.
E) H0 is $\mu$ $\neq$ 2. H1 is $\mu$ > 2.

Question 31

A restaurant that bills its house account monthly is concerned that the average monthly bill exceeds $200 per account. A random sample of twelve accounts is selected, resulting in a sample mean of $220 and a standard deviation of $12. The t-test is to be conducted at the 5% level of significance. The t-value is calculated to be 5.77. At the 0.01 level of significance, what is your decision?

A) You reject the null hypothesis, and agree that the average monthly bill exceeds $200.
B) You have insufficient evidence to reject the null hypothesis.
C) You reject the alternate hypothesis and agree that the average monthly bill is less than $200.
D) You should have used the z-test.

Question 32

If the alternate hypothesis states that $\mu$ does not equal 4,000, what is the rejection region for the hypothesis test?

A) Both tails
B) Lower or left tail
C) Upper or right tail
D) Center

Question 33

Records on a fleet of trucks reveal that the average life of a set of spark plugs is normally distributed with a mean of 35,600 kilometres. A manufacturer of spark plugs claims that its plugs have an average life in excess of 35,600 kilometres. The fleet owner purchased 18 sets and found that the sample average life was 37,700 kilometres, the sample standard deviation was 2415 kilometres and the computed t = 3.677.

A) Based on these findings, there is enough evidence to accept the manufacturer's claim at the 0.05 level.
B) Based on these findings, there is NOT enough evidence to accept the manufacturer's claim at the 0.05 level.
C) Based on these findings, there is enough evidence to accept the manufacturer's claim at the 0.05 level, but NOT at the 0.01 level.
D) Based on these findings, there is NOT enough evidence to accept the manufacturer's claim at the 0.01 level.
E) Based on these findings, there in NOT enough evidence to accept the manufacturer's claim at either the 0.05 or the 0.01 level.

Question 34

What do we call the statement that determines if the null hypothesis is rejected?

A) Decision rule
B) Test statistic
C) Alternate hypothesis
D) Critical value

Question 35

It is claimed that in a bushel of peaches less than ten percent are defective. A sample of 400 peaches is examined and 50 are found to be defective. What is the alternate hypothesis for a one-sided test?

A) p $\neq$ 0.10
B) p > 0.10
C) p $\le$ 0.10
D) p = 0.10
E) p < 0.10

Question 36

A restaurant that bills its house account monthly is concerned that the average monthly bill exceeds $200 per account. A random sample of twelve accounts is selected, resulting in a sample mean of $220 and a standard deviation of $12. The t-test is to be conducted at the 5% level of significance.

A) The null hypothesis is $\mu$ $\le$ 200. The alternate hypothesis is $\mu$ $\le$ 200.
B) The null hypothesis is $\mu$ $\le$ 200. The alternate hypothesis is $\mu$ > 200.
C) The null hypothesis is $\mu$ = 200. The alternate hypothesis is $\mu$ $\neq$ 200.
D) The null hypothesis is $\mu$ > 200. The alternate hypothesis is $\mu$ $\le$ 200
E) The null hypothesis is $\mu$ $\le$ 220. The alternate hypothesis is $\mu$ > 220.

Question 37

Which of the following is NOT one of the five steps in the hypothesis testing procedure?

A) Formulate a decision rule
B) State the null and alternate hypotheses
C) Select a level for $\beta$
D) Identify the test statistic

Question 38

The mean length of a small counter balance bar is 43 millimeters. There is concern that the adjustments of the machine producing the bars have changed. Test the claim at the 0.02 level that there has been no change in the mean length. The alternate hypothesis is that there has been a change. Twelve bars (n = 12) were selected at random and their lengths recorded. The lengths are (in millimeters) 42, 39, 42, 45, 43, 40, 39, 41, 40, 42, 43 and 42. The mean of the sample is 41.5 and the standard deviation 1.784. Computed t = -2.913. Has there been a statistically significant change in the mean length of the bars?

A) Yes, because the computed t lies in the area beyond the critical.
B) No, because the information given is not complete.
C) No, because the computed t lies in the area to the right of -2.718.

Question 39

A restaurant that bills its house account monthly is concerned that the average monthly bill exceeds $200 per account. A random sample of twelve accounts is selected, resulting in a sample mean of $220 and a standard deviation of $12. The t-test is to be conducted at the 5% level of significance.

A) The critical value of t is +1.796. The calculated value of t is +5.77.
B) The critical value of t is -1.796. The calculated value of t is -5.77.
C) The critical value of t is +2.201. The calculated value of t is +5.77.
D) The critical value of t is +2.201. The calculated value of t is +1.40.
E) The critical value of t is +2.201. The calculated value of t is -5.77.

Question 40

i. For a one-tailed test using the 0.05 level of significance, the critical value for the z test is 1.645, but for t it is 1.96. ii. For a one-tailed test using the 0.01 level of significance, the critical value for the z-test is 1.645, but for t it is 1.96.
iii. For a two-tailed test using the 0.05 level of significance the critical value for the z-test is 1.96 and it is the same for the t-test.

A) (i), (ii), and (iii) are all correct statements.
B) (i) is a correct statement but not (ii) or (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

Question 41

If the 1% level of significance is used and the computed value of z is +6.00, what is our decision?

A) Do not reject H₀
B) Reject H₀
C) Reject H₁

Question 42

If $\alpha$ = 0.05 for a two-tailed test, how large is the acceptance area?

A) 0.050
B) 0.025
C) 0.950
D) 0.975

Question 43

The following summarizes the average of the TSE 300 Index at the end of 20 randomly selected weeks in 2000. 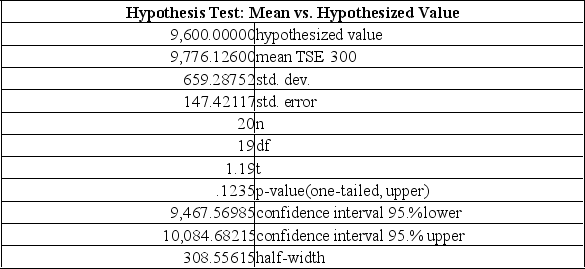Using a 5% level of significance, can it be agreed that the Index average was more than $9,600 during the year 2000?

A) Fail to reject the null hypothesis and conclude the mean index was 9,600.
B) Reject the null hypothesis and conclude the mean index was lower than 9,600.
C) Reject the null hypothesis and conclude the mean index was greater than 9,600.
D) Reject the null hypothesis and conclude the mean index was different from 9,600.

Question 44

What is the critical z-value for a one-tailed lower test at the 1% level of risk?

A) +2.58
B) -2.58
C) +2.33
D) -2.33

Question 45

A manufacturer claims that less than 1% of all his products do not meet the minimum government standards. A survey of 500 products revealed ten did not meet the standard. If the z-statistic is -2.054 and the level of significance is 0.03, what is your decision?

A) You reject the null hypothesis, and agree that less than 1% fail to meet government standards.
B) You have insufficient evidence to reject the null hypothesis.
C) You reject the alternate hypothesis and agree that less than 1% meet government standards.
D) You should have used the t-test.

Question 46

For a one-tailed hypothesis test, the critical z-value of the test statistic is -2.33. Which of the following is true about the hypothesis test?

A) $\alpha$ = 0.05 for a lower-tailed test
B) $\alpha$ = 0.01 for a lower-tailed test
C) $\alpha$ = 0.05 for an upper-tailed test
D) $\alpha$ = 0.01 for an upper-tailed test

Question 47

A manufacturer wants to increase the absorption capacity of a sponge. Based on past data, the average sponge could absorb 103.5ml. After the redesign, the absorption amounts of a sample of sponges were (in millilitres): 121.3, 109.2, 97.6, 103.5, 112.4, 115.3, 106.5, 112.4, 118.3, and 115.3. What is the decision rule at the 0.01 level of significance to test if the new design increased the absorption amount of the sponge?

A) Do not reject null hypothesis if computed t is less than 2.580
B) Do not reject null hypothesis if computed t is less than 2.821
C) Reject null hypothesis if computed z is 1.96 or larger
D) Reject null hypothesis if computed t is less than 2.764

Question 48

A nationwide survey of college students was conducted and found that students spend two hours per class hour studying. A professor at your school wants to determine whether the time students spend at your school is significantly different from the two hours. A random sample of fifteen statistics students is carried out and the findings indicate an average of 1.75 hours with a standard deviation of 0.24 hours. Given the following printout, what can you determine?

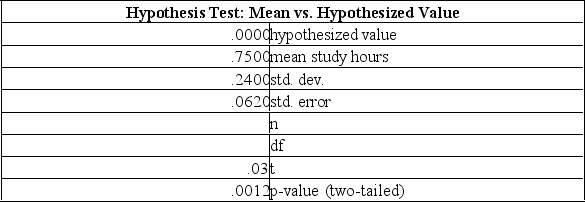
A) The alternate hypothesis is $\mu$ $\le$ 2
B) You should accept the null hypothesis at the 0.05 level of significance.
C) There is less than a 1% chance of getting these results if the null hypothesis is true, so you have very strong evidence to suggest that the average number of study hours is different from 2.
D) You should reject the null hypothesis at the 0.05 level of significance, but accept it when testing at the 0.01 level of significance.
E) You should accept the null hypothesis at the 0.05 level of significance, but reject it when testing at the 0.01 level of significance.

Question 49

The mean gross annual incomes of certified tack welders are normally distributed with the mean of $50,000 and a standard deviation of $4,000. The ship building association wishes to find out whether their tack welders earn more or less than $50,000 annually. The alternate hypothesis is that the mean is not $50,000. If the level of significance is 0.10, what is the decision rule?

A) Do not reject the null hypothesis if computed z lies between -1.65 and +1.65; otherwise, reject it.
B) Do not reject the null hypothesis if computed z is greater than 1.65; otherwise, reject it.
C) Do not reject the null hypothesis if computed z lies between -1.96 and +1.96; otherwise, reject it.
D) Reject the null hypothesis if computed z is below -1.96; otherwise, reject it.

Question 50

A manufacturer of stereo equipment introduces new models in the fall. Retail dealers are surveyed immediately after the Christmas selling season regarding their stock on hand of each piece of equipment. It has been discovered that unless 40% of the new equipment ordered by the retailers in the fall had been sold by Christmas, immediate production cutbacks are needed. The manufacturer has found that contacting all of the dealers after Christmas by mail is frustrating as many of them never respond. This year 80 dealers were selected at random and telephoned regarding a new receiver. It was discovered that 38% of those receivers had been sold. Since 38% is less than 40%, does this mean that immediate production cutbacks are needed or can this difference of 2 percentage points be attributed to sampling? Test at the 0.05 level. Computed z = -0.37.

A) Cut back production
B) Do not cut back production
C) Cannot determine based on information given

Question 51

A manufacturer claims that less than 1% of all his products do not meet the minimum government standards. A survey of 500 products revealed ten did not meet the standard. If the z-statistic is -2.58 and the level of significance is 0.02, what is your decision?

A) You reject the null hypothesis, and agree that less than 1% fail to meet government standards.
B) You have insufficient evidence to reject the null hypothesis.
C) You reject the alternate hypothesis and agree that less than 1% meet government standards.
D) You should have used the t-test.

Question 52

To conduct a test of hypothesis with a small sample, we need to be able to make the following assumption that:

A) a larger computed value of t will be needed to reject the null hypothesis.
B) the region of acceptance will be wider than for large samples.
C) the confidence interval will be wider than for large samples.
D) the population is normally distributed.

Question 53

The mean gross annual incomes of certified tack welders are normally distributed with the mean of $50,000 and a standard deviation of $4,000. The ship building association wishes to find out whether their tack welders earn more or less than $50,000 annually. The alternate hypothesis is that the mean is not $50,000. If the level of significance is 0.10, what is the critical value?

A) 1.65
B) 2.58
C) 1.28
D) $\pm$ 1.28
E) $\pm$ 1.645

Question 54

Which of the following is a test statistic used to test a hypothesis about a population?

A) $\alpha$
B) $\beta$
C) $\mu$
D) z

Question 55

A manufacturer wants to increase the shelf life of a line of cake mixes. Past records indicate that the average shelf life of the mix is 216 days. After a revised mix has been developed, a sample of nine boxes of cake mix gave these shelf lives (in days): 215, 217, 218, 219, 216, 217, 217, 218 and 218. At the 0.025 level, has the shelf life of the cake mix increased?

A) Yes, because computed t is greater than the critical value.
B) Yes, because computed t is less than the critical value.
C) No, because computed t lies in the region of acceptance.
D) No, because 217.24 is quite close to 216.

Question 56

A manufacturer claims that less than 1% of all his products do not meet the minimum government standards. A survey of 500 products revealed ten did not meet the standard. If the computed value of z = -2.25 and the level of significance is 0.03, what is your decision?

A) You reject the null hypothesis, and agree that less than 1% fail to meet government standards.
B) You have insufficient evidence to reject the null hypothesis.
C) You reject the alternate hypothesis and agree that less than 1% meet government standards.
D) You should have used the t-test.

Question 57

What is the critical value for t in a one-tailed hypothesis test in which a null hypothesis is tested at the 5% level of significance based on a sample size of 15?

A) 1.708
B) 1.711
C) 1.761
D) 2.145

Question 58

For a two-tailed test at the 0.05 significance level, what is the rejection region when the population standard deviation is known?

A) Between $\pm$ 1.96
B) Between $\pm$ 1.65
C) Greater than +1.96 and less than -1.96
D) Greater than +1.65 and less than -1.65

Question 59

What does z equal for an $\alpha$ = 0.01 and a lower level test?

A) +2.33
B) -2.33
C) +2.58
D) -2.58

Question 60

A machine is set to fill the small size packages of Smarties candies with 56 candies per bag. A sample revealed: 3 bags of 56, 2 bags of 57, 1 bag of 55, and 2 bags of 58. How many degrees of freedom are there?

A) 9
B) 1
C) 8
D) 7

Question 61

The average cost of tuition, room and board at community colleges is reported to be $8,500 per year with a standard deviation of $1,200, but a financial administrator believes that the average cost is higher. A study conducted using 150 community colleges showed that the average cost per year is $9,000. Let $\alpha$ = 0.05. What is the critical z-value for this test?

A) +1.96
B) -1.96
C) +1.65
D) -1.65

Question 62

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. Does this sample support the original claim? What is the decision for a statistical significant change in average weights at birth at the 5% level of significance?

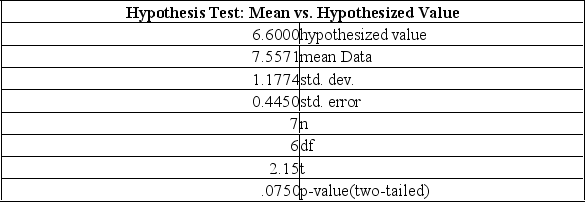
A) Fail to reject the null hypothesis and conclude the mean is 6.6 lb.
B) Reject the null hypothesis and conclude the mean is higher than 6.6 lb.
C) Reject the null hypothesis and conclude the mean is lower than 6.6 lb.
D) Cannot calculate because population standard deviation is unknown.

Question 63

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. What is the sample variance?

A) 1.177
B) 6.6
C) 1.385
D) 7.6

Question 64

One of the major U.S. tire makers wishes to review its warranty for their rainmaker tire. The warranty is for 40,000 miles. The tire company believes that the tire actually lasts more than 40,000 miles. A sample 49 tires revealed that the mean number of miles is 45,000 miles with a standard deviation of 15,000 miles. Test the hypothesis with a 0.05 significance level.

A) H0 is $\mu$ $\ge$ 40,000 H1 is $\mu$ > 40,000
B) H0 is $\mu$ = 40,000 H1 is $\mu$ > 40,000
C) H0 is $\mu$ $\le$ 40,000 H1 is $\mu$ = 40,000
D) H0 is $\mu$ = 40,000 H1 is $\mu$ $\neq$ 40,000

Question 65

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. What is the sample standard deviation?

A) 1.177
B) 6.6
C) 1.385
D) 7.6

Question 66

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. What are the degrees of freedom associated with this claim?

A) 7
B) 8
C) 6
D) 6.6
E) 7.6

Question 67

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. Does this sample support the original claim? The null hypothesis is:

A) $\mu$ = 6.6
B) $\mu$ $\neq$ 6.6
C) $\mu$ $\ge$ 6.6
D) $\mu$ > 7.6
E) $\mu$ $\neq$ 7.6

Question 68

The printout below refers to the weekly closing stock prices for Air Canada on 20 randomly selected weeks in 2000. 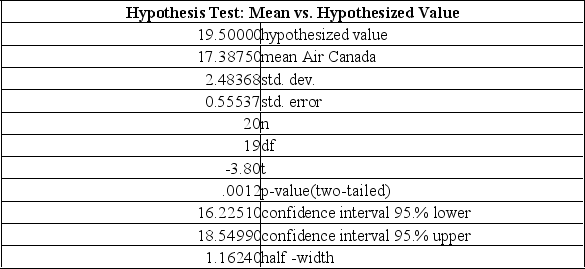Using a 5% level of significance, can you say that the average Air Canada stock price was different from $19.50?

A) Fail to reject the null hypothesis and conclude the mean stock price was $19.50.
B) Reject the null hypothesis and conclude the mean stock price was lower than $19.50.
C) Reject the null hypothesis and conclude the mean index was greater than $19.50.
D) Reject the null hypothesis and conclude the mean index was different from $19.50.

Question 69

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. What is the sample mean?

A) 6.6
B) 7.6
C) 1.177
D) 2.447

Question 70

One of the major U.S. tire makers wishes to review its warranty for their rainmaker tire. The warranty is for 40,000 miles. The tire company believes that the tire actually lasts more than 40,000 miles with a standard deviation of 15,000 miles. A sample 49 tires revealed that the mean number of miles is 45,000 miles. Test the hypothesis with a 0.05 significance level.

A) The decision rule is to reject if Z > 1.645. The calculated value of z is +2.33.
B) The decision rule is to reject if Z < 1.645. The calculated value of z is -2.33.
C) The decision rule is to reject if Z > 1.96. The calculated value of z is +2.33.
D) The decision rule is to reject if Z < 1.96. The calculated value of z is +2.33.

Question 71

The average cost of tuition, room and board at community colleges is reported to be $8,500 per year with a standard deviation of $1,200, but a financial administrator believes that the average cost is higher. A study conducted using 150 community colleges showed that the average cost per year is $9,000. Let $\alpha$ = 0.05. Given the z-statistic is 5.1, what is our decision about the average cost?

A) Equal to $8,500
B) Greater than $8,500
C) Less than $8,500
D) Not equal to $8,500

Question 72

Given: null hypothesis is that the population mean is 16.9 against the alternative hypothesis that the population mean is not equal to 16.9. A random sample of 16 items results in a sample mean of 17.1 and the sample standard deviation is 2.4. It can be assumed that the population is normally distributed. Determine the observed "t" value.

A) t = 2.12
B) t = 1.33
C) t = 1.753
D) t = 0.33

Question 73

The dean of a business school claims that the average starting salary of its graduates is more than $50,000. It is known that the population standard deviation is $10,000. Sample data on the starting salaries of 20 randomly selected recent graduates yielded a mean of $55,000. What is the value of the sample test statistic?

A) z = 2.24
B) t = 7.2
C) t = 5.04
D) t = 2.24

Question 74

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. If $\alpha$ = 0.05, what is the critical t value?

A) -2.365
B) $\pm$ 1.96
C) $\pm$ 2.365
D) $\pm$ 2.447
E) -2.447

Question 75

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. Does this sample support the original claim? What is the alternate hypothesis?

A) $\mu$ = 6.6
B) $\mu$ $\neq$ 6.6
C) $\mu$ $\ge$ 6.6
D) $\mu$ > 7.6
E) $\mu$ $\neq$ 7.6

Question 76

The dean of a business school claims that the average starting salary of its graduates is more than $50,000. It is known that the population standard deviation is $10,000. Sample data on the starting salaries of 36 randomly selected recent graduates yielded a mean of $62,000. What is the value of the sample test statistic?

A) z = 7.2
B) t = 5.04
C) z = 2.7
D) z = 5.6

Question 77

The dean of a business school claims that the average starting salary of its graduates is more than $50,000. It is known that the population standard deviation is $10,000. Sample data on the starting salaries of 25 randomly selected recent graduates yielded a mean of $52,000. What is the value of the sample test statistic?

A) z = 1.0
B) t = 7.2
C) t = 5.04
D) t = 1.22

Question 78

The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. Does this sample support the original claim? What is the decision for a significant increase in the average birthrate at a 5% level of significance?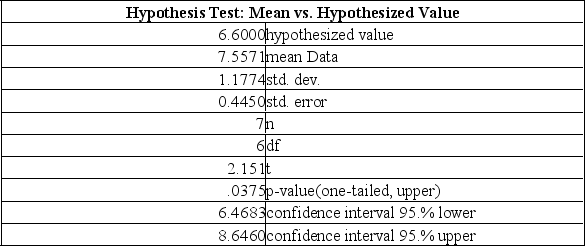

A) Fail to reject the null hypothesis and conclude the mean is 6.6 lb.
B) Reject the null hypothesis and conclude the mean is lower than 6.6 lb.
C) Reject the null hypothesis and conclude the mean is greater than 6.6 lb.
D) Cannot calculate because population standard deviation is unknown.

Question 79

The dean of a business school claims that the average starting salary of its graduates is more than $50,000. It is known that the population standard deviation is $10,000. Sample data on the starting salaries of 36 randomly selected recent graduates yielded a mean of $52,000. What is the value of the sample test statistic?

A) z = 1.2
B) t = 7.2
C) t = 0.12
D) t = 1.22

Question 80

One of the major U.S. tire makers wishes to review its warranty for their rainmaker tire. The warranty is for 40,000 miles. The tire company believes that the tire actually lasts more than 40,000 miles with a standard deviation of 15,000 miles. A sample 49 tires revealed that the mean number of miles is 45,000 miles. Test the hypothesis with a 0.05 significance level.

A) At a 5% level of significance, our decision is to reject the null hypothesis. The tires last more than 40 000 miles.
B) At a 5% level of significance, our decision is to accept the null hypothesis. The tires last 40,000 miles.
C) At a 5% level of significance, we should have used the t-test, rather than the z-test.