Deck 4: Probability and Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/113
Play
Full screen (f)
Deck 4: Probability and Probability Distributions
1
There are two types of random variables,they are
A)discrete and continuous
B)exhaustive and mutually exclusive
C)complementary and cumulative
D)real and unreal
A)discrete and continuous
B)exhaustive and mutually exclusive
C)complementary and cumulative
D)real and unreal
A
2
If two events are mutually exclusive,what is the probability that both occur at the same time?
A)0.00
B)0.50
C)1.00
D)Cannot be determined from the information given.
A)0.00
B)0.50
C)1.00
D)Cannot be determined from the information given.
A
3
If events A and B are mutually exclusive,then the probability of both events occurring simultaneously is equal to
A)0.0
B)0.5
C)1.0
D)any value between 0.5 and 1.0
A)0.0
B)0.5
C)1.0
D)any value between 0.5 and 1.0
A
4
Probabilities that cannot be estimated from long-run relative frequencies of events are
A)objective probabilities
B)subjective probabilities
C)complementary probabilities
D)joint probabilities
A)objective probabilities
B)subjective probabilities
C)complementary probabilities
D)joint probabilities

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
5
If two events are collectively exhaustive,what is the probability that one or the other occurs?
A)0.25
B)0.50
C)1.00
D)Cannot be determined from the information given.
A)0.25
B)0.50
C)1.00
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
6
Let A and B be the events of the FDA approving and rejecting a new drug to treat hypertension,respectively.The events A and B are:
A)independent
B)conditional
C)unilateral
D)mutually exclusive
A)independent
B)conditional
C)unilateral
D)mutually exclusive

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
7
The law of large numbers is relevant to the estimation of
A)objective probabilities
B)subjective probabilities
C)both of these options
D)neither of these options
A)objective probabilities
B)subjective probabilities
C)both of these options
D)neither of these options

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
8
The joint probabilities shown in a table with two rows, 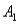 and
and 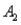 and two columns,
and two columns, 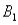 and
and 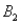 ,are as follows: P(
,are as follows: P( 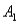 and
and  )= .10,P(
)= .10,P( 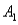 and
and  )= .30,P(
)= .30,P( 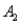 and
and 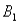 )= .05,and P(
)= .05,and P( 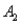 and
and  )= .55.Then P(
)= .55.Then P( 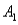 |
| 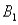 ),calculated up to two decimals,is
),calculated up to two decimals,is
A).33
B).35
C).65
D).67
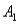 and
and 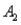 and two columns,
and two columns, 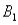 and
and 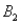 ,are as follows: P(
,are as follows: P( 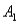 and
and  )= .10,P(
)= .10,P( 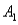 and
and  )= .30,P(
)= .30,P( 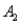 and
and 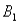 )= .05,and P(
)= .05,and P( 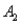 and
and  )= .55.Then P(
)= .55.Then P( 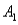 |
| 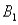 ),calculated up to two decimals,is
),calculated up to two decimals,isA).33
B).35
C).65
D).67

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
9
If two events are mutually exclusive and collectively exhaustive,what is the probability that both occur?
A)0.00
B)0.50
C)1.00
D)Cannot be determined from the information given.
A)0.00
B)0.50
C)1.00
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
10
A discrete probability distribution:
A)lists all of the possible values of the random variable and their corresponding probabilities
B)is a tool that can be used to incorporate uncertainty into models
C)can be estimated from long-run proportions
D)is the distribution of a single random variable
A)lists all of the possible values of the random variable and their corresponding probabilities
B)is a tool that can be used to incorporate uncertainty into models
C)can be estimated from long-run proportions
D)is the distribution of a single random variable

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following statements are true?
A)Probabilities must be nonnegative
B)Probabilities must be less than or equal to 1
C)The sum of all probabilities for a random variable must be equal to 1
D)All of these options are true.
A)Probabilities must be nonnegative
B)Probabilities must be less than or equal to 1
C)The sum of all probabilities for a random variable must be equal to 1
D)All of these options are true.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
12
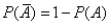 is the:
is the:A)addition rule
B)commutative rule
C)rule of complements
D)rule of opposites

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
13
If two events are collectively exhaustive,what is the probability that both occur at the same time?
A)0.00
B)0.50
C)1.00
D)Cannot be determined from the information given.
A)0.00
B)0.50
C)1.00
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
14
Probabilities that can be estimated from long-run relative frequencies of events are
A)objective probabilities
B)subjective probabilities
C)complementary probabilities
D)joint probabilities
A)objective probabilities
B)subjective probabilities
C)complementary probabilities
D)joint probabilities

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
15
A function that associates a numerical value with each possible outcome of an uncertain event is called a
A)conditional variable
B)random variable
C)population variable
D)sample variable
A)conditional variable
B)random variable
C)population variable
D)sample variable

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
16
The probability of an event and the probability of its complement always sum to:
A)1
B)0
C)any value between 0 and 1
D)any positive value
A)1
B)0
C)any value between 0 and 1
D)any positive value

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
17
The formal way to revise probabilities based on new information is to use:
A)complementary probabilities
B)conditional probabilities
C)unilateral probabilities
D)common sense probabilities
A)complementary probabilities
B)conditional probabilities
C)unilateral probabilities
D)common sense probabilities

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
18
If P(A)= P(A|B),then events A and B are said to be
A)mutually exclusive
B)independent
C)exhaustive
D)complementary
A)mutually exclusive
B)independent
C)exhaustive
D)complementary

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
19
If A and B are mutually exclusive events with P(A)= 0.70,then P(B):
A)can be any value between 0 and 1
B)can be any value between 0 and 0.70
C)cannot be larger than 0.30
D)Cannot be determined with the information given
A)can be any value between 0 and 1
B)can be any value between 0 and 0.70
C)cannot be larger than 0.30
D)Cannot be determined with the information given

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
20
If two events are mutually exclusive,what is the probability that one or the other occurs?
A)0.25
B)0.50
C)1.00
D)Cannot be determined from the information given.
A)0.25
B)0.50
C)1.00
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following best describes the concept of marginal probability?
A)It is a measure of the likelihood that a particular event will occur,regardless of whether another event occurs.
B)It is a measure of the likelihood that a particular event will occur,given that another event has already occurred.
C)It is a measure of the likelihood of the simultaneous occurrence of two or more events.
D)None of the above.
A)It is a measure of the likelihood that a particular event will occur,regardless of whether another event occurs.
B)It is a measure of the likelihood that a particular event will occur,given that another event has already occurred.
C)It is a measure of the likelihood of the simultaneous occurrence of two or more events.
D)None of the above.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
22
If A and B are any two events with P(A)= .8 and P(B| 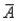 )= .7,then P(
)= .7,then P( 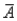 and B)is
and B)is
A).56
B).14
C).24
D)None of the above
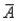 )= .7,then P(
)= .7,then P( 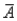 and B)is
and B)isA).56
B).14
C).24
D)None of the above

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
23
You think you have a 90% chance of passing your statistics class.This is an example of subjective probability.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
24
If two events are independent,what is the probability that they both occur?
A)0
B)0.50
C)1.00
D)Cannot be determined from the information given
A)0
B)0.50
C)1.00
D)Cannot be determined from the information given

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
25
A random variable is a function that associates a numerical value with each possible outcome of a random phenomenon.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
26
Probability is a number between 0 and 1,inclusive,which measures the likelihood that some event will occur.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
27
If events A and B have nonzero probabilities,then they can be both independent and mutually exclusive.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
28
If A and B are mutually exclusive events with P(A)= 0.30 and P(B)= 0.40,then the probability that either A or B or both occur is:
A)0.10
B)0.12
C)0.70
D)None of the above
A)0.10
B)0.12
C)0.70
D)None of the above

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
29
If A and B are independent events with P(A)= 0.40 and P(B)= 0.50,then P(A/B)is 0.50.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
30
Two events A and B are said to be independent if P(A and B)= P(A)+ P(B)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
31
When we wish to determine the probability that at least one of several events will occur,we would use the addition rule.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
32
Two or more events are said to be exhaustive if one of them must occur.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
33
The joint probabilities shown in a table with two rows,  and
and  and two columns,
and two columns, 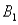 and
and 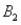 ,are as follows: P(
,are as follows: P( 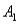 and
and 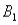 )= .10,P(
)= .10,P( 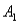 and
and  )= .30,P(
)= .30,P(  and
and 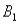 )= .05,and P(
)= .05,and P( 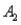 and
and 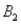 )= .55.Then P(
)= .55.Then P( 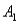 |
| 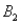 ),calculated up to two decimals,is
),calculated up to two decimals,is
A).33
B).35
C).65
D).67
 and
and  and two columns,
and two columns, 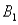 and
and 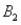 ,are as follows: P(
,are as follows: P( 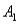 and
and 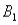 )= .10,P(
)= .10,P( 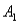 and
and  )= .30,P(
)= .30,P(  and
and 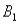 )= .05,and P(
)= .05,and P( 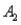 and
and 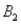 )= .55.Then P(
)= .55.Then P( 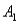 |
| 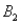 ),calculated up to two decimals,is
),calculated up to two decimals,isA).33
B).35
C).65
D).67

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
34
The number of cars produced by GM during a given quarter is a continuous random variable.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
35
Conditional probability is the probability that an event will occur,with no other events taken into consideration.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
36
The law of large numbers states that subjective probabilities can be estimated based on the long run relative frequencies of events

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
37
If P(A)= 0.25 and P(B)= 0.65,then P(A and B)is:
A)0.25
B)0.40
C)0.90
D)Cannot be determined from the information given
A)0.25
B)0.40
C)0.90
D)Cannot be determined from the information given

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
38
The probability that event A will not occur is denoted as 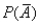 .
.
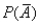 .
.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
39
If P(A and B)= 1,then A and B must be collectively exhaustive.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
40
If A and B are any two events with P(A)= .8 and P(B|A)= .4,then the joint probability of A and B is
A).80
B).40
C).32
D)1.20
A).80
B).40
C).32
D)1.20

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
41
When two events are independent,they are also mutually exclusive.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
42
Two events are said to be independent when knowledge of one event is of no value when assessing the probability of the other.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
43
The number of people entering a shopping mall on a given day is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
44
The relative frequency of an event is the number of times the event occurs out of the total number of times the random experiment is run.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
45
Two events A and B are said to mutually be exclusive if P(A and B)= 0.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
46
The time students spend in a computer lab during one day is an example of a continuous random variable.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
47
If A and B are two independent events with P(A)= 0.20 and P(B)= 0.60,then P(A and B)= 0.80

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
48
Given that events A and B are independent and that P(A)= 0.8 and P(B/A)= 0.4,then P(A and B)= 0.32.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
49
Suppose that after graduation you will either buy a new car (event A)or take a trip to Europe (event B).Events A and B are mutually exclusive.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
50
Football teams toss a coin to see who will get their choice of kicking or receiving to begin a game.The probability that given team will win the toss three games in a row is 0.125.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
51
The number of car insurance policy holders is an example of a discrete random variable.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
52
Suppose A and B are mutually exclusive events where P(A)= 0.3 and P(B)= 0.4,then P(A and B)= 0.12.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
53
The multiplication rule for two events A and B is: P(A and B)= P(A|B)P(A).

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
54
If P(A and B)= 0,then A and B must be collectively exhaustive.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose A and B are two events where P(A)= 0.5,P(B)= 0.4,and P(A and B)= 0.2,then P(B/A)= 0.5.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
56
Marginal probability is the probability that a given event will occur,given that another event has already occurred.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
57
Two or more events are said to be mutually exclusive if at most one of them can occur.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
58
The temperature of the room in which you are writing this test is a continuous random variable.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
59
Suppose A and B are mutually exclusive events where P(A)= 0.2 and P(B)= 0.5,then P(A or B)= 0.70.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
60
Two or more events are said to be exhaustive if at most one of them can occur.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
61
What is the probability that this project will not be completed on time?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
62
What is the probability that the price of this product will be above its mean in the upcoming quarter?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
63
Determine the marginal probability distribution of 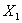 .
.
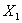 .
.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
64
What is the probability that no one is waiting or being served in the regular checkout line?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
65
Find the marginal distribution of Y.What does this distribution tell you?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
66
On average,how many customers would you expect to see in each of these two lines at the grocery store?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
67
What is the probability that the demand of this product exceed 2500 units in the upcoming quarter,given that its price will be less than $30?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
68
What is the probability that the demand of this product will be below its mean in the upcoming quarter?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
69
Find the marginal distribution of X.What does this distribution tell you?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
70
What is the probability that no one is waiting or being served in the express checkout line?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
71
What is the probability that this project will be completed in less than 4 months from now?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
72
(A)Calculate the conditional distribution of X given Y.
(B)What is the practical benefit of knowing the conditional distribution in (A)?
(B)What is the practical benefit of knowing the conditional distribution in (A)?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
73
What is the probability that no more than two customers are waiting in both lines combined?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
74
Calculate the conditional distribution of Y given X.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
75
Find the probability distribution of X.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
76
Find the expected price and demand level for the upcoming quarter.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
77
Calculate the joint probabilities of 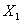 and
and 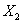 .
.
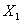 and
and 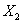 .
.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
78
What is the probability that the demand of this product will be less than 3500 units in the upcoming quarter,given that its price will be greater than $20?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
79
Are  and
and 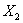 independent random variables? Explain why or why not.
independent random variables? Explain why or why not.
 and
and 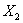 independent random variables? Explain why or why not.
independent random variables? Explain why or why not.
Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
80
(A)What is the expected completion time (in months)from now for this project?
(B)How much variability (in months)exists around the expected value found in (A)?
(B)How much variability (in months)exists around the expected value found in (A)?

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck



