Deck 16: Simultaneous Equations Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 16: Simultaneous Equations Models
1
Exclusion restrictions are said to be imposed in a two-equation simultaneous equations model if it is assumed that:
A)certain exogenous variables do not appear in the first equation and others are absent from the second equation.
B)certain endogenous variables do not appear in the first equation and others are absent from the second equation.
C) the error terms in each equation is correlated with the exogenous variables.
D) the error terms in each equation is uncorrelated with the exogenous variables.
A)certain exogenous variables do not appear in the first equation and others are absent from the second equation.
B)certain endogenous variables do not appear in the first equation and others are absent from the second equation.
C) the error terms in each equation is correlated with the exogenous variables.
D) the error terms in each equation is uncorrelated with the exogenous variables.
A
Explanation: Exclusion restrictions are said to be imposed in a two-equation simultaneous equations model if it is assumed that certain exogenous variables do not appear in the first equation and others are absent from the second equation.
Explanation: Exclusion restrictions are said to be imposed in a two-equation simultaneous equations model if it is assumed that certain exogenous variables do not appear in the first equation and others are absent from the second equation.
2
Which of the following statements is true?
A)White test can be used to efficiently determine the presence of serial correlation in panel data.
B)The t statistic is not an efficient test to determine serial correlation in panel data.
C) Instrumental variables for both endogenous and exogenous variables are required for estimating simultaneous equation models concerned with panel data.
D) 2SLS should be applied to simultaneous equation models with panel data only after removing the unobserved effects from the equations of interest.
A)White test can be used to efficiently determine the presence of serial correlation in panel data.
B)The t statistic is not an efficient test to determine serial correlation in panel data.
C) Instrumental variables for both endogenous and exogenous variables are required for estimating simultaneous equation models concerned with panel data.
D) 2SLS should be applied to simultaneous equation models with panel data only after removing the unobserved effects from the equations of interest.
D
Explanation: 2SLS should be applied to simultaneous equation models with panel data only after removing the unobserved effects from the equations of interest.
Explanation: 2SLS should be applied to simultaneous equation models with panel data only after removing the unobserved effects from the equations of interest.
3
Which of the following correctly highlights a limitation of applying simultaneous equation models to time series data?
A)Most time series have variables with a unit root and 2SLS is complicated when applied to equations with such variables.
B)2SLS estimates are inefficient when applied to variables that are not in their levels but in first differences.
C) It is difficult to form simultaneous equations which satisfy the rank and order conditions using time series data.
D) The problem of serial correlation greatly limits the efficiency of simultaneous equation models and leads to inefficient estimations.
A)Most time series have variables with a unit root and 2SLS is complicated when applied to equations with such variables.
B)2SLS estimates are inefficient when applied to variables that are not in their levels but in first differences.
C) It is difficult to form simultaneous equations which satisfy the rank and order conditions using time series data.
D) The problem of serial correlation greatly limits the efficiency of simultaneous equation models and leads to inefficient estimations.
A
Explanation: Most time series have variables with a unit root and 2SLS is complicated when applied to equations with such variables.
Explanation: Most time series have variables with a unit root and 2SLS is complicated when applied to equations with such variables.
4
In econometrics, simultaneity arises when:
A)strictly exogenous explanatory variables determine the dependent variable through a step-by-step process.
B)the error term is correlated with both the dependent variable and explanatory variables.
C) one or more of the explanatory variables is jointly determined with the dependent variable.
D) both serial correlation and heteroskedasticity are present in an hypothesized model.
A)strictly exogenous explanatory variables determine the dependent variable through a step-by-step process.
B)the error term is correlated with both the dependent variable and explanatory variables.
C) one or more of the explanatory variables is jointly determined with the dependent variable.
D) both serial correlation and heteroskedasticity are present in an hypothesized model.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following equations is an overidentified equation?
A)y1 = α12y2 + α13y3 + β11z1 + u1
B)y2 = α21y1 + β21z2 + β23z3 + u2
C) y3 = α32y1 + β31z1 + β32z2 + β33z3 + β34z4 + u3
D) y1 = β10 + α1y2+ z1β1 + u1
A)y1 = α12y2 + α13y3 + β11z1 + u1
B)y2 = α21y1 + β21z2 + β23z3 + u2
C) y3 = α32y1 + β31z1 + β32z2 + β33z3 + β34z4 + u3
D) y1 = β10 + α1y2+ z1β1 + u1

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
An alternative to using simultaneous equation models with panel data is:
A)to use OLS estimates after first differencing the data.
B)to use fixed effects transformation on the equations and then apply 2SLS.
C) to convert the equations into reduced form and then apply feasible generalized least squares.
D) to convert the equations into reduced form and then apply OLS.
A)to use OLS estimates after first differencing the data.
B)to use fixed effects transformation on the equations and then apply 2SLS.
C) to convert the equations into reduced form and then apply feasible generalized least squares.
D) to convert the equations into reduced form and then apply OLS.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
The following simultaneous equations describe the demand and supply for a particular good in a competitive market. Qi =  1Pi +
1Pi + 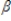 1zi1 + ui1
1zi1 + ui1
Qi = 2Pi +
2Pi + 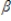 2zi2 + ui2
2zi2 + ui2
Which of the following are the endogenous variables in this model?
A)Pi, zi1, and zi2
B)Pi and Qi
C) zi1, and zi2
D) ui1 and ui2
 1Pi +
1Pi + 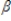 1zi1 + ui1
1zi1 + ui1Qi =
 2Pi +
2Pi + 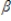 2zi2 + ui2
2zi2 + ui2Which of the following are the endogenous variables in this model?
A)Pi, zi1, and zi2
B)Pi and Qi
C) zi1, and zi2
D) ui1 and ui2

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
In a simultaneous equations model, if any variable is determined outside of the model, then it is considered a(n):
A)endogenous variable.
B)random variable.
C) exogenous variable.
D) error variable.
A)endogenous variable.
B)random variable.
C) exogenous variable.
D) error variable.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
Which of the following correctly identifies a characteristic of structural equations?
A)A structural equation should contain equal number of dependent and independent variables.
B)A structural equation should contain equal number of endogenous and exogenous variables.
C) A structural equation should have a behavioral, ceteris paribus interpretation on its own.
D) A structural equation should not contain structural errors.
A)A structural equation should contain equal number of dependent and independent variables.
B)A structural equation should contain equal number of endogenous and exogenous variables.
C) A structural equation should have a behavioral, ceteris paribus interpretation on its own.
D) A structural equation should not contain structural errors.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
10
The following equations represent a simultaneous equations model: K1 =  1K2 +
1K2 + 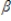 1z1 + u1
1z1 + u1
K2 = 2K1+
2K1+ 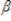 2z2 + u2
2z2 + u2
The reduced form equation for K2 will express:
A)K1 as a function of K2 and the error terms.
B)K2 as a function of K1and the error terms.
C) K2 as a function of exogenous variables and the error terms.
D) K1 as a function of exogenous variables, the error terms, and K2.
 1K2 +
1K2 + 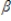 1z1 + u1
1z1 + u1K2 =
 2K1+
2K1+ 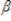 2z2 + u2
2z2 + u2The reduced form equation for K2 will express:
A)K1 as a function of K2 and the error terms.
B)K2 as a function of K1and the error terms.
C) K2 as a function of exogenous variables and the error terms.
D) K1 as a function of exogenous variables, the error terms, and K2.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
Refer to the simultaneous equations model above. The reduced form error from the reduced form equation for K2 will be a:
A)quadratic function of u1 and u2, and correlated with z1 and z2.
B)quadratic function of u1 and u2, and uncorrelated with z1 and z2.
C) linear function of u1 and u2, and correlated with z1 and z2.
D) linear function of u1 and u2, and uncorrelated with z1 and z2.
A)quadratic function of u1 and u2, and correlated with z1 and z2.
B)quadratic function of u1 and u2, and uncorrelated with z1 and z2.
C) linear function of u1 and u2, and correlated with z1 and z2.
D) linear function of u1 and u2, and uncorrelated with z1 and z2.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
An equation in the simultaneous equations model satisfies the order condition for identification if:
A)the number of excluded endogenous variables from the equation is at most as large as the number of right-hand side exogenous variables.
B)the number of excluded endogenous variables from the equation is at least as large as the number of right-hand side exogenous variables.
C) the number of excluded exogenous variables from the equation is at most as large as the number of right-hand side endogenous variables.
D) the number of excluded exogenous variables from the equation is at least as large as the number of right-hand side endogenous variables.
A)the number of excluded endogenous variables from the equation is at most as large as the number of right-hand side exogenous variables.
B)the number of excluded endogenous variables from the equation is at least as large as the number of right-hand side exogenous variables.
C) the number of excluded exogenous variables from the equation is at most as large as the number of right-hand side endogenous variables.
D) the number of excluded exogenous variables from the equation is at least as large as the number of right-hand side endogenous variables.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following is a method which can be used for estimation in simultaneous equations models?
A)Feasible generalized least squares estimation
B)Prais-Winsten transformation
C) Cochrane-Orcutt transformation
D) Two stage least squares estimation
A)Feasible generalized least squares estimation
B)Prais-Winsten transformation
C) Cochrane-Orcutt transformation
D) Two stage least squares estimation

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following statements is true?
A)The use of 2SLS is applicable to simultaneous equations model with at most two equations.
B)Identification of simultaneous equations with three or more equations is based on matrix algebra.
C) 2SLS method used in the estimation of simultaneous equations is an example of a system estimation method.
D) The maximum number of equations permissible for a simultaneous equations model is four.
A)The use of 2SLS is applicable to simultaneous equations model with at most two equations.
B)Identification of simultaneous equations with three or more equations is based on matrix algebra.
C) 2SLS method used in the estimation of simultaneous equations is an example of a system estimation method.
D) The maximum number of equations permissible for a simultaneous equations model is four.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
OLS is biased and inconsistent when applied to a structural equation in a simultaneous equations system.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
A predetermined variable in a simultaneous equations model is:
A)a constant.
B)the error term.
C) a lagged variable.
D) an omitted variable.
A)a constant.
B)the error term.
C) a lagged variable.
D) an omitted variable.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
The following equations represent a two-equation model: y1 = β10 + α1y2 + z1β1 + u1
Y2 = β20 + α2y1 + z2β2 + u2
Where, y1 and y2 are the:
A)endogenous variables.
B)structural error terms.
C) exogenous variables.
D) intercepts.
Y2 = β20 + α2y1 + z2β2 + u2
Where, y1 and y2 are the:
A)endogenous variables.
B)structural error terms.
C) exogenous variables.
D) intercepts.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
The rank condition for identification of a structural equation states that the first equation in a two-equation simultaneous equations model is identified if, and only if:
A)the first equation contains at least one exogenous variable (with a nonzero coefficient) that is excluded from the second equation.
B)the first equation contains at least two exogenous variables (with a nonzero coefficient) that are excluded from the second equation.
C) the second equation contains at least one exogenous variable (with a nonzero coefficient) that is excluded from the first equation.
D) the second equation contains at least two exogenous variables (with a nonzero coefficient) that are excluded from the first equation.
A)the first equation contains at least one exogenous variable (with a nonzero coefficient) that is excluded from the second equation.
B)the first equation contains at least two exogenous variables (with a nonzero coefficient) that are excluded from the second equation.
C) the second equation contains at least one exogenous variable (with a nonzero coefficient) that is excluded from the first equation.
D) the second equation contains at least two exogenous variables (with a nonzero coefficient) that are excluded from the first equation.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19
A simultaneous equations model is suitable whenever two variables are determined simultaneously.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20
The following equations represent a simultaneous equations model: K1 =  1K2 +
1K2 + 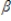 1z1 + u1
1z1 + u1
K2 = 2K1+
2K1+ 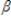 2z2 + u2
2z2 + u2
OLS will suffer from simultaneity bias if:
A)u1 is correlated with z1.
B)z1 is correlated with z2.
C) K2 is correlated with u1.
D) K1 is correlated with u1.
 1K2 +
1K2 + 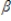 1z1 + u1
1z1 + u1K2 =
 2K1+
2K1+ 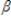 2z2 + u2
2z2 + u2OLS will suffer from simultaneity bias if:
A)u1 is correlated with z1.
B)z1 is correlated with z2.
C) K2 is correlated with u1.
D) K1 is correlated with u1.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
If a structured model contains a time trend-which may capture exogenous, trending factors that are not directly modeled-then the trend acts as its own instrumental variable.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
22
The first step in estimating simultaneous equations models (SEMs) with panel data is to find instrumental variables for the endogenous variables in the transformed equation.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
The order condition is a necessary and sufficient condition for identification of an equation in a simultaneous equations model.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
The number of overidentifying restrictions equals the total number of exogenous variables in the system plus the total number of explanatory variables in the equation.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
The instrumental variables in the two stage least squares estimation method consists of endogenous variables appearing in either equation.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck



