Deck 15: Waiting Line Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/66
Play
Full screen (f)
Deck 15: Waiting Line Models
1
When a waiting system is in steady-state operation,the number of units in the system is not changing.
False
2
Before waiting lines can be analyzed economically,the arrivals' cost of waiting must be estimated.
True
3
For all waiting lines,P0 + Pw = 1.
False
4
In a multiple channel system it is more efficient to have a separate waiting line for each channel.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
5
If some maximum number of customers is allowed in a queuing system at one time,the system has a finite calling population.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
6
If service time follows an exponential probability distribution,approximately 63% of the service times are less than the mean service time.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
7
Little's flow equations indicate that the relationship of L to Lq is the same as that of W to Wq.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
8
For an M/M/1 queuing system,if the service rate,µ,is doubled,the average wait in the system,W,is cut in half.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
9
Queue discipline refers to the manner in which waiting units are arranged for service.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
10
In waiting line systems where the length of the waiting line is limited,the mean number of units entering the system might be less than the arrival rate.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
11
When blocked customers are cleared,an important decision is how many channels to provide.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
12
Use of the Poisson probability distribution assumes that arrivals are not random.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
13
Waiting line models describe the transient-period operating characteristics of a waiting line.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
14
Queue discipline refers to the assumption that a customer has the patience to remain in a slow moving queue.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
15
A multiple-channel system has more than one waiting line.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
16
A waiting line situation where every customer waits in the same line before being served by the same server is called a single server waiting line.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
17
For an M/M/k system,the average number of customers in the system equals the customer arrival rate times the average time a customer spends waiting in the system.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
18
For a single-channel waiting line,the utilization factor is the probability that an arriving unit must wait for service.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
19
Adding more channels always improves the operating characteristics of the waiting line and reduces the waiting cost.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
20
In developing the total cost for a waiting line,waiting cost takes into consideration both the time spent waiting in line and the time spent being served.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
21
The total cost for a waiting line does NOT specifically depend on
A)the cost of waiting.
B)the cost of service.
C)the number of units in the system.
D)the cost of a lost customer.
A)the cost of waiting.
B)the cost of service.
C)the number of units in the system.
D)the cost of a lost customer.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
22
Little's flow equations apply to any waiting line model.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
23
Decision makers in queuing situations attempt to balance
A)operating characteristics against the arrival rate.
B)service levels against service cost.
C)the number of units in the system against the time in the system.
D)the service rate against the arrival rate.
A)operating characteristics against the arrival rate.
B)service levels against service cost.
C)the number of units in the system against the time in the system.
D)the service rate against the arrival rate.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
24
In a waiting line situation,arrivals occur,on average,every 10 minutes,and 10 units can be received every hour.What are λ and μ?
A)λ = 10,μ = 10
B)λ = 6,μ = 6
C)λ = 6,μ = 10
D)λ = 10,μ = 6
A)λ = 10,μ = 10
B)λ = 6,μ = 6
C)λ = 6,μ = 10
D)λ = 10,μ = 6

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
25
With no waiting allowed,operating characteristics Lq and Wq are automatically zero regardless of the number of servers.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
26
In a multiple channel system
A)each server has its own queue.
B)each server has the same service rate.
C)μ > λ
D)All of the alternatives are correct.
A)each server has its own queue.
B)each server has the same service rate.
C)μ > λ
D)All of the alternatives are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
27
Little's flow equations
A)require Poisson and exponential assumptions.
B)are applicable to any waiting line model.
C)require independent calculation of W,L,Wq,and Lq.
D)All of the alternatives are correct.
A)require Poisson and exponential assumptions.
B)are applicable to any waiting line model.
C)require independent calculation of W,L,Wq,and Lq.
D)All of the alternatives are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
28
In waiting line applications,the exponential probability distribution indicates that approximately 63 percent of the service times are less than the mean service time.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
29
The assumption of exponentially distributed service times indicates that
A)37% of the service times are less than the mean service time.
B)50% of the service times are less than the mean service time.
C)63% of the service times are less than the mean service time.
D)service time increase at an exponential rate as the waiting line grows.
A)37% of the service times are less than the mean service time.
B)50% of the service times are less than the mean service time.
C)63% of the service times are less than the mean service time.
D)service time increase at an exponential rate as the waiting line grows.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
30
For many waiting line situations,the arrivals occur randomly and independently of other arrivals and it has been found that a good description of the arrival pattern is provided by
A)a normal probability distribution.
B)an exponential probability distribution.
C)a uniform probability distribution.
D)a Poisson probability distribution.
A)a normal probability distribution.
B)an exponential probability distribution.
C)a uniform probability distribution.
D)a Poisson probability distribution.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
31
Performance measures dealing with the number of units in line and the time spent waiting are called
A)queuing facts.
B)performance queues.
C)system measures.
D)operating characteristics.
A)queuing facts.
B)performance queues.
C)system measures.
D)operating characteristics.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
32
If arrivals occur according to the Poisson distribution every 20 minutes,then which is NOT true?
A)λ = 20 arrivals per hour
B)λ = 3 arrivals per hour
C)λ = 1/20 arrivals per minute
D)λ = 72 arrivals per day
A)λ = 20 arrivals per hour
B)λ = 3 arrivals per hour
C)λ = 1/20 arrivals per minute
D)λ = 72 arrivals per day

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
33
The arrival rate in queuing formulas is expressed as
A)the mean time between arrivals.
B)the minimum number of arrivals per time period.
C)the mean number of arrivals per channel.
D)the mean number of arrivals per time period.
A)the mean time between arrivals.
B)the minimum number of arrivals per time period.
C)the mean number of arrivals per channel.
D)the mean number of arrivals per time period.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
34
What queue discipline is assumed by the waiting line models presented in the textbook?
A)first-come first-served.
B)last-in first-out.
C)shortest processing time first.
D)No discipline is assumed.
A)first-come first-served.
B)last-in first-out.
C)shortest processing time first.
D)No discipline is assumed.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
35
Operating characteristics formulas for the single-channel queue do NOT require
A)λ ≥ μ.
B)Poisson distribution of arrivals.
C)an exponential distribution of service times.
D)an FCFS queue discipline.
A)λ ≥ μ.
B)Poisson distribution of arrivals.
C)an exponential distribution of service times.
D)an FCFS queue discipline.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
36
The manner in which units receive their service,such as FCFS,is the
A)queue discipline.
B)channel.
C)steady state.
D)operating characteristic.
A)queue discipline.
B)channel.
C)steady state.
D)operating characteristic.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following can NOT be found by the queuing formulas presented in the textbook?
A)the probability that no units are in the system.
B)the average number of units in the system.
C)the maximum time a unit spends in the system.
D)the average time a unit spends in the system.
A)the probability that no units are in the system.
B)the average number of units in the system.
C)the maximum time a unit spends in the system.
D)the average time a unit spends in the system.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
38
For a single-server queuing system,the average number of customers in the waiting line is one less than the average number in the system.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
39
Single-booth ticket sales at a theater would be an example of which queuing model?
A)single-channel,Poisson service rate distribution,unlimited queue length.
B)single-channel,Poisson service rate distribution,limited queue length.
C)single-channel,constant service rate distribution,unlimited queue length.
D)single-channel,normal service rate distribution,unlimited queue length.
A)single-channel,Poisson service rate distribution,unlimited queue length.
B)single-channel,Poisson service rate distribution,limited queue length.
C)single-channel,constant service rate distribution,unlimited queue length.
D)single-channel,normal service rate distribution,unlimited queue length.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
40
Models with a finite calling population
A)have an arrival rate independent of the number of units in the system.
B)have a service rate dependent on the number of units in the system.
C)use the size of the population as a parameter in the operating characteristics formulas.
D)All of the alternatives are correct.
A)have an arrival rate independent of the number of units in the system.
B)have a service rate dependent on the number of units in the system.
C)use the size of the population as a parameter in the operating characteristics formulas.
D)All of the alternatives are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
41
Circle Electric Supply is considering opening a second service counter to better serve the electrical contractor customers.The arrival rate is 10 per hour.The service rate is 14 per hour.If the cost of waiting is $30 and the cost of each service counter is $22 per hour,then should the second counter be opened?

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
42
The post office uses a multiple channel queue,where customers wait in a single line for the first available window.If the average service time is 1 minute and the arrival rate is 7 customers every five minutes,find,when two service windows are open,
a.the probability both windows are idle.
b.the probability a customer will have to wait.
c.the average time a customer is in line.
d.the average time a customer is in the post office.
a.the probability both windows are idle.
b.the probability a customer will have to wait.
c.the average time a customer is in line.
d.the average time a customer is in the post office.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
43
The average time a unit spends in the waiting line equals
A)Lq times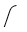
B)Lq times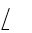
C)Lq divided by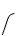
D)Lq divided by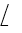
A)Lq times
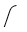
B)Lq times
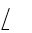
C)Lq divided by
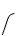
D)Lq divided by
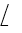

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
44
The equations provided in the textbook for computing operating characteristics apply to a waiting line operating
A)at start-up.
B)at steady-state.
C)at peak-demand times.
D)in transition
A)at start-up.
B)at steady-state.
C)at peak-demand times.
D)in transition

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
45
The 8 students in a seminar class must come to the professor's office to turn in a paper and give a 5-minute oral summary.Assume there is a service rate of 10 per hour and adequate time is available for all.The arrival rate for each unit is 5 per hour.What is the probability there is no one in the office or waiting when you come?

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
46
A company has tool cribs where workmen draw parts.Two men have applied for the position of distributing parts to the workmen.George Fuller is fresh out of trade school and expects a $6 per hour salary.His average service time is 4 minutes.John Cox is a veteran who expects $12 per hour.His average service time is 2 minutes.A workman's time is figured at $10 per hour.Workmen arrive to draw parts at an average rate of 12 per hour.
a.What is the average waiting time a workman would spend in the system under each applicant?
b.Which applicant should be hired?
a.What is the average waiting time a workman would spend in the system under each applicant?
b.Which applicant should be hired?

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
47
Arrivals at a box office in the hour before the show follow the Poisson distribution with λ = 7 per minute.Service times are constant at 7.5 seconds.Find the average length of the waiting line.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
48
Quick Clean Rooter cleans out clogged drains.Due to the competitive nature of the drain cleaning business,if a customer calls Quick Clean and finds the line busy,they immediately try another company and Quick Clean loses the business.
Quick Clean management estimates that on the average,a customer tries to call Quick Clean every three minutes and the average time to take a service order is 200 seconds.The company wishes to hire enough operators so that at most 4% of its potential customers get the busy signal.
a.How many operators should be hired to meet this objective?
b.Given your answer to a),what is the probability that all the operators are idle?
Quick Clean management estimates that on the average,a customer tries to call Quick Clean every three minutes and the average time to take a service order is 200 seconds.The company wishes to hire enough operators so that at most 4% of its potential customers get the busy signal.
a.How many operators should be hired to meet this objective?
b.Given your answer to a),what is the probability that all the operators are idle?

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
49
The Sea View Resort uses a multiple-channel queue registration system.If the average service time is 8 minutes,there are three registration clerks,and guests arrive at the rate of one every 5 minutes,find
a.λ and μ.
b.the probability all three clerks are idle.
c.the probability a guest will have to wait.
d.the average time a customer is in line.
e.the average number of customers in line.
a.λ and μ.
b.the probability all three clerks are idle.
c.the probability a guest will have to wait.
d.the average time a customer is in line.
e.the average number of customers in line.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
50
During summer weekdays,boats arrive at the inlet drawbridge according to the Poisson distribution at a rate of 3 per hour.In a 2-hour period,
a.what is the probability that no boats arrive?
b.what is the probability that 2 boats arrive?
c.what is the probability that 8 boats arrive?
a.what is the probability that no boats arrive?
b.what is the probability that 2 boats arrive?
c.what is the probability that 8 boats arrive?

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
51
The assumption that arrivals follow a Poisson probability distribution is equivalent to the assumption that the time between arrivals has
A)a normal probability distribution
B)an exponential probability distribution
C)a uniform probability distribution
D)a Poisson probability distribution
A)a normal probability distribution
B)an exponential probability distribution
C)a uniform probability distribution
D)a Poisson probability distribution

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
52
For an M/G/1 system with λ = 6 and μ = 9,with σ = .03,find
a.the probability the system is idle.
b.the average length of the queue.
c.the average number in the system.
a.the probability the system is idle.
b.the average length of the queue.
c.the average number in the system.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
53
The time to process a registration at the Sea View Resort follows the exponential distribution and has a mean of 6 minutes.
a.What is the probability of a registration time shorter than 3 minutes?
b.What is the probability of a registration time shorter than 6 minutes?
c.What is the probability of a registration time between 3 and 6 minutes?
a.What is the probability of a registration time shorter than 3 minutes?
b.What is the probability of a registration time shorter than 6 minutes?
c.What is the probability of a registration time between 3 and 6 minutes?

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
54
The Grand Movie Theater has one box office clerk.On average,each customer that comes to see a movie can be sold its ticket at the rate of 6 per minute.For the theater's normal offerings of older movies,customers arrive at the rate of 3 per minute.Assume arrivals follow the Poisson distribution and service times follow the exponential distribution.
a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Grand has booked the Stars Wars Trilogy and expects more customers.From conversations with other theater owners,it estimates that the arrival rate will increase to 10 per minute.Output is supplied for a two-cashier and a three-cashier system.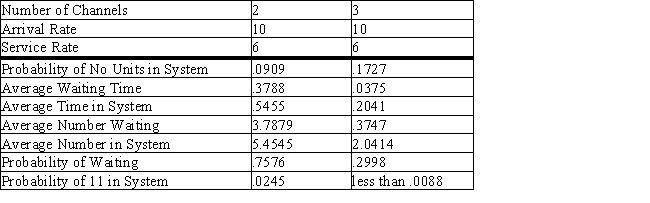
a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Grand has booked the Stars Wars Trilogy and expects more customers.From conversations with other theater owners,it estimates that the arrival rate will increase to 10 per minute.Output is supplied for a two-cashier and a three-cashier system.


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
55
The insurance department at Shear's has two agents,each working at a mean speed of 8 customers per hour.Customers arrive at the insurance desk at a mean rate of one every six minutes and form a single queue.Management feels that some customers are going to find the wait at the desk too long and take their business to Word's,Shear's competitor.
In order to reduce the time required by an agent to serve a customer Shear's is contemplating installing one of two minicomputer systems: System A which leases for $18 per day and will increase an agent's efficiency by 25%;or,System B which leases for $23 per day and will increase an agent's efficiency by 50%.Agents work 8-hour days.
If Shear's estimates its cost of having a customer in the system at $3 per hour,determine if Shear's should install a new minicomputer system,and if so,which one.
In order to reduce the time required by an agent to serve a customer Shear's is contemplating installing one of two minicomputer systems: System A which leases for $18 per day and will increase an agent's efficiency by 25%;or,System B which leases for $23 per day and will increase an agent's efficiency by 50%.Agents work 8-hour days.
If Shear's estimates its cost of having a customer in the system at $3 per hour,determine if Shear's should install a new minicomputer system,and if so,which one.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
56
The machine repair problem is an application of the M/M/1 model with
A)no waiting line.
B)arbitrary service times.
C)a finite calling population.
D)blocked customers cleared.
A)no waiting line.
B)arbitrary service times.
C)a finite calling population.
D)blocked customers cleared.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
57
The Quick Snap photo machine at the Lemon County bus station takes four snapshots in exactly 75 seconds.Customers arrive at the machine according to a Poisson distribution at the mean rate of 20 per hour.On the basis of this information,determine the following:
a.the average number of customers waiting to use the photo machine
b.the average time a customer spends in the system
c.the probability an arriving customer must wait for service.
a.the average number of customers waiting to use the photo machine
b.the average time a customer spends in the system
c.the probability an arriving customer must wait for service.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
58
The Arctic Flyers minor league hockey team has one box office clerk.On average,each customer that comes to see a game can be sold a ticket at the rate of 8 per minute.For normal games,customers arrive at the rate of 5 per minute.Assume arrivals follow the Poisson distribution and service times follow the exponential distribution.
a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Flyers are playing in the league playoffs and anticipate more fans,estimating that the arrival rate will increase to 12 per minute.Output is supplied for a two-cashier and a three-cashier system.

a.What is the average number of customers waiting in line?
b.What is the average time a customer spends in the waiting line?
c.What is the average number of customers in the system?
d.What is a customer's average time in the system?
e.What is the probability that someone will be buying tickets when an arrival occurs?
The Flyers are playing in the league playoffs and anticipate more fans,estimating that the arrival rate will increase to 12 per minute.Output is supplied for a two-cashier and a three-cashier system.



Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
59
For an M/G/1 system with λ = 20 and μ = 35,with σ = .005,find
a.the probability the system is idle.
b.the average length of the queue.
c.the average number in the system.
a.the probability the system is idle.
b.the average length of the queue.
c.the average number in the system.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
60
Andy Archer,Ph.D. ,is a training consultant for six mid-sized manufacturing firms.On the average,each of his six clients calls him for consulting assistance once every 25 days.Andy typically spends an average of five days at the client's firm during each consultation.
Assuming that the time between client calls follows an exponential distribution,determine the following:
a.the average number of clients Andy has on backlog
b.the average time a client must wait before Andy arrives to it
c.the proportion of the time Andy is busy
Assuming that the time between client calls follows an exponential distribution,determine the following:
a.the average number of clients Andy has on backlog
b.the average time a client must wait before Andy arrives to it
c.the proportion of the time Andy is busy

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
61
List six steady-state operating characteristics for a single-channel waiting line with Poisson arrivals and exponential
service times.
service times.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
62
How can a system be changed to improve the service rate?

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
63
Discuss the importance of the utilization factor in a queuing system and the assumptions made about its value.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
64
Diagram the servers and arrivals in the single and multiple channel models.Designate the line and the system.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
65
Explain what is meant by the following statement,"operating characteristics are non-optimizing."

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
66
Give examples of systems you have seen in which a)blocked arrivals are cleared,and b)there is a finite calling
population.
population.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck



