
Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Edition 12ISBN: 978-1133189022
Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Edition 12ISBN: 978-1133189022 Exercise 6
A common utility function used to illustrate economic examples is the Cobb-Douglas function where U(X, Y)= XaYb where a and b are decimal exponents that sum to 1.0 (that is, for example, 0.3 and 0.7).
a. Explain why the utility function used in problem and problem 2.3 is a special case of this function.
b. For this utility function, the MRS is given by MRS = MUx/MUy = aY/bX. Use this fact together with the utility-maximizing condition (and that a + b = 1) to show that this person will spend the fraction of his or her income on good X and the fraction of income on good Y-that is, show PxX/I = a, PyY/I = b.
c. Use the results from part b to show that total spending on good X will not change as the price of X changes so long as income stays constant.
d. Use the results from part b to show that a change in the price of Y will not affect the quantity of X purchased.
e. Show that with this utility function, a doubling of income with no change in prices of goods will cause a precise doubling of purchases of both X and Y.
Problem Suppose the person faced with the budget constraint described in problem 2.1 has preferences for apples (A) and bananas (B) given by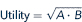
a. If A = 5 and B = 80, what will utility be?
b. If A = 10, what value for B will provide the same utility as in part a?
c. If A = 20, what value for B will provide the same utility as in parts a and b?
d. Graph the indifference curve implied by parts a through c.
e. Given the budget constraint from problem, which of the points identified in parts a through c can be bought by this person?
f. Show through some examples that every other way of allocating income provides less utility than does the point identified in part b. Graph this utility-maximizing situation.
Problem Paul derives utility only from CDs and DVDs. His utility function is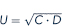
a. Sketch Paul's indifference curves for U = 5, U = 10, and U = 20.
b. Suppose Paul has $200 to spend and that CDs cost $5 and DVDs cost $20. Draw Paul s budget constraint on the same graph as his indifference curves.
c. Suppose Paul spends all of his income on DVDs. How many can he buy and what is his utility?
d. Show that Paul's income will not permit him to reach the U = 20 indifference curve.
e. If Paul buys 5 DVDs, how many CDs can he buy? What is his utility?
f. Use a carefully drawn graph to show that the utility calculated in part e is the highest Paul can achieve with his $200.
a. Explain why the utility function used in problem and problem 2.3 is a special case of this function.
b. For this utility function, the MRS is given by MRS = MUx/MUy = aY/bX. Use this fact together with the utility-maximizing condition (and that a + b = 1) to show that this person will spend the fraction of his or her income on good X and the fraction of income on good Y-that is, show PxX/I = a, PyY/I = b.
c. Use the results from part b to show that total spending on good X will not change as the price of X changes so long as income stays constant.
d. Use the results from part b to show that a change in the price of Y will not affect the quantity of X purchased.
e. Show that with this utility function, a doubling of income with no change in prices of goods will cause a precise doubling of purchases of both X and Y.
Problem Suppose the person faced with the budget constraint described in problem 2.1 has preferences for apples (A) and bananas (B) given by
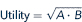
a. If A = 5 and B = 80, what will utility be?
b. If A = 10, what value for B will provide the same utility as in part a?
c. If A = 20, what value for B will provide the same utility as in parts a and b?
d. Graph the indifference curve implied by parts a through c.
e. Given the budget constraint from problem, which of the points identified in parts a through c can be bought by this person?
f. Show through some examples that every other way of allocating income provides less utility than does the point identified in part b. Graph this utility-maximizing situation.
Problem Paul derives utility only from CDs and DVDs. His utility function is
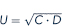
a. Sketch Paul's indifference curves for U = 5, U = 10, and U = 20.
b. Suppose Paul has $200 to spend and that CDs cost $5 and DVDs cost $20. Draw Paul s budget constraint on the same graph as his indifference curves.
c. Suppose Paul spends all of his income on DVDs. How many can he buy and what is his utility?
d. Show that Paul's income will not permit him to reach the U = 20 indifference curve.
e. If Paul buys 5 DVDs, how many CDs can he buy? What is his utility?
f. Use a carefully drawn graph to show that the utility calculated in part e is the highest Paul can achieve with his $200.
Explanation
a) The utility function used in problem ...
Intermediate Microeconomics and Its Application 12th Edition by Walter Nicholson,Christopher Snyder
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255



